Example: One of the possible practical applications of Bayes' theorem could be found in jurisprudence. Suppose that a test for using a particular drug is 97% sensitive and 98% specific. That is, the test will produce 97% true positive results for drug users and 98% true negative results for non-drug users. Suppose that 0.7% of people are users of the drug. What is the probability that a randomly selected individual with a positive test is a drug user? Even if an individual tests positive, it is more likely that they do not use the drug than that they do. This is because the number of non-users is large compared to the number of users. The number of false positives outweighs the number of true positives. For example, if 1000 individuals are tested, there are expected to be 995 non-users and 5 users. From the 995 non-users, 0.01 × 995 ≃ 10 false positives are expected. From the 5 users, 0.99 × 5 ≈ 5 true positives are expected. Out of 15 positive results, only 5 are genuine.

The importance of specificity in this example can be seen by calculating that even if sensitivity is raised to 100% and specificity remains at 99% then the probability of the person being a drug user only rises from 33.2% to 33.4%, but if the sensitivity is held at 99% and the specificity is increased to 99.5% then the probability of the person being a drug user rises to about 49.9%.

Example: Suppose you are given the following information regarding a cancer testing scenario:

• 1% of women have breast cancer (and therefore 99% do not).
• 80% of mammograms detect breast cancer when it is there (and therefore 20% miss it).
• 9.6% of mammograms detect breast cancer when it’s not there (and therefore 90.4% correctly return a negative result).

Put in a table, the probabilities look like this:

Now suppose you get a positive test result. What are the chances you have cancer? 80%? 99%? 1%?

• Tests are not the event. We have a cancer test, separate from the event of actually having cancer. We have a test for spam, separate from the event of actually having a spam message.

• Tests are flawed. Tests detect things that don’t exist (false positive), and miss things that do exist (false negative).

• Tests give us test probabilities, not the real probabilities. People often consider the test results directly, without considering the errors in the tests.

• False positives skew results. Suppose you are searching for something really rare (1 in a million). Even with a good test, it’s likely that a positive result is really a false positive on somebody in the 999,999.

• People prefer natural numbers. Saying “100 in 10,000″ rather than “1%” helps people work through the numbers with fewer errors, especially with multiple percentages (“Of those 100, 80 will test positive” rather than “80% of the 1% will test positive”).

• Even science is a test. At a philosophical level, scientific experiments can be considered “potentially flawed tests” and need to be treated accordingly. There is a test for a chemical, or a phenomenon, and there is the event of the phenomenon itself. Our tests and measuring equipment have some inherent rate of error.

The table looks like this:

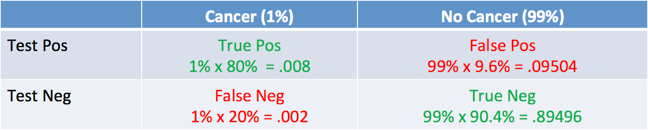
And what was the question again? Oh yes: what’s the chance we really have cancer if we get a positive result. The chance of an event is the number of ways it could happen given all possible outcomes:

Probability = desired event / all possibilities

The chance of getting a real, positive result is .008. The chance of getting any type of positive result is the chance of a true positive plus the chance of a false positive (.008 + 0.09504 = .10304).

So, our chance of cancer is .008/.10304 = 0.0776, or about 7.8%.    ■

Example: Each bag in a large box contains 25 tulip bulbs. Three-fourths of the bags are of Type A containing bulbs for 5 red and 20 yellow tulips; one-fourth of the bags are of Type B contain bulbs for 15 red and 10 yellow tulips. A bag is selected at random and one bulb is planted. What is the probability that the bulb will produce a red tulip?

If A denotes the event that a Type A bag is selected, then, because 75% of the bags are of Type A, Pr(A) = 0.75. If B denotes the event that a Type B bag is selected, then, because 25% of the bags are of Type B, Pr(B) = 0.25. Let R denote the event that the selected bulb produces a red tulip. Then:

What is the probability that the bulb will produce a yellow tulip? If the tulip is red, what is the probability that a bag having 15 red and 10 yellow tulips was selected?