Consider a systems of linear differential equations \( \dot{\bf x} = {\bf A}\,{\bf x}. \)
Its phase portrait is a geometric representation of the trajectories of a dynamical system in the phase plane. A sketch
of a particular solution in the phase plane is called the trajectory of the solution. Its solutions are plotted as parametric curves
(with t as the parameter) on the Cartesian plane tracing the path of each
particular solution \( {\bf x} = ( x_1 (t) , x_2 (t) ), \ -\infty
Similar to a direction field for a single differential equation, a phase portrait is a graphical tool to visualize
how the solutions of a given system of differential equations would behave in the long run. Each set of initial conditions is represented by a different curve, or point. They consist of a plot of typical trajectories in the state space. This reveals information such as whether an attractor, a repellor or limit cycle is present for the chosen parameter value.
Recall that an equilibrium solution of the autonoumous system \( \dot{\bf x} = {\bf f} ({\bf x}) \) is
a point \( {\bf x}^{\ast} = ( x_1^{\ast} , x_2^{\ast} ) \) where the derivative of \( {\bf x}(t) \) is zero.
An equilibrium solution is a constant solution of
the system, and is usually called a critical point. For a linear system \( \dot{\bf x} = {\bf A}\,{\bf x}, \)
an equilibrium solution occurs at each solution of the system (of
homogeneous algebraic equations) \( {\bf A}\,{\bf x} = {\bf 0} . \) As we have seen, such a system
has exactly one solution, located at the origin, if \( \det{\bf A} \ne 0 .\) If
\( \det{\bf A} = 0 , \)
then there are infinitely many solutions. As a rulle, we will only consider systems
of linear differential equations whose coefficient matrix A has nonzero
determinant.
We are going to classify the critical points of various systems of first order linear differential
equations by their stability. In addition, due to the truly two-dimensional
nature of the parametric curves, we will also classify the type of those
critical points by their shapes (or, rather, by the shape formed by the
trajectories about each critical point). Their classification is based on eigenvalues of the coefficient matrix.
Therefore, we consider different cases.
Case 1: Distinct real eigenvalues of the same sign. Then the general solution of the linear system \( \dot{\bf x} = {\bf A}\,{\bf x}, \) is
\[
{\bf x} (t) = c_1 \,{\bf \xi} \, e^{\lambda_1 t} + c_2 \,{\bf \eta} \, e^{\lambda_2 t} ,
\]
where \( \lambda_1 \) and \( \lambda_2 \) are distinct real eiegnvalues, \( {\bf \xi} \) and \( {\bf \eta} \) are
corresponding eigenvectors, and \( c_1 , c_2 \) are arbitrary real constants.
When \( \lambda_1 \) and \( \lambda_2 \) are both positive,
or are both negative, the phase portrait shows trajectories either moving away from the
critical point to infinite-distant away (when \( \lambda >0 \) ), or moving directly
toward, and converge to the critical point (when \( \lambda <0 . \)
The trajectories that are the eigenvectors move in straight lines. The rest
of the trajectories move, initially when near the critical point, roughly
in the same direction as the eigenvector of the eigenvalue with the
smaller absolute value. Then, farther away, they would bend toward
the direction of the eigenvector of the eigenvalue with the larger
absolute value The trajectories either move away from the critical
point to infinite-distant away (when λ are both positive), or move
toward from infinite-distant out and eventually converge to the critical
point (when λ are both negative). This type of critical point is called a
node. It is asymptotically stable if λ are both negative, unstable if λ are both positive.
Stability: It is unstable if both eigenvalues are positive;
asymptotically stable if they are both negative.
Case 2: Distinct real eigenvalues are of opposite signs. In this type of phase portrait, the trajectories given by the eigenvectors
of the negative eigenvalue initially start at infinite-distant away, move
toward and eventually converge at the critical point. The trajectories
that represent the eigenvectors of the positive eigenvalue move in
exactly the opposite way: start at the critical point then diverge to
infinite-distant out. Every other trajectory starts at infinite-distant
away, moves toward but never converges to the critical point, before
changing direction and moves back to infinite-distant away. All the
while it would roughly follow the 2 sets of eigenvectors. This type of
critical point is called a saddle point. It is always unstable
Stability: It is always unstable.
Case 3: Repeated real eigenvalue. Then we have two subcases: either the eigenvalue is
not defective or defective. In the latter case, there are two linearly independent eigenvectors \( {\bf \xi} \) and \( {\bf \eta} .\)
Then the general solution is
\[
{\bf x} (t) = c_1 \,{\bf \xi} \, e^{\lambda\, t} + c_2 \,{\bf \eta} \, e^{\lambda\, t} ,
\]
where \( \lambda \) is the repeated eigenvalue and \( c_1 , c_2 \) are arbitrary real constants.
Every nonzero solution traces a straight-line trajectory, in the
direction given by the vector \( c_1 \,{\bf \xi} + c_2 \,{\bf \eta} .\) The phase portrait
thus has a distinct star-burst shape. The trajectories either move directly
away from the critical point to infinite-distant away (when \( \lambda >0 ,\) or
move directly toward, and converge to the critical point (when \( \lambda <0 .\) )
This type of critical point is called a proper node (or a star point). It
is asymptotically stable if \( \lambda <0 ,\) unstable if \( \lambda >0 .\)
Stability: It is unstable if the eigenvalue is positive; asymptotically
stable if the eigenvalue is negative.
Example. For \( 2 \times 2 \) systems of linear differential equations, this will
occur if, and only if, when the coefficient matrix A is a constant
multiple of the identity matrix:
\[
\alpha \, \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} = \begin{bmatrix} \alpha &0 \\ 0&\alpha \end{bmatrix} \quad \mbox{ where }
\alpha \quad \mbox{is an arbitrary nonzero constant} .
\]
When there is only one linearly independent eigenvector \( {\bf \xi} , \) the eigenvalue
λ is defective, and the general solution is
\[
{\bf x} (t) = c_1 \,{\bf \xi} \, e^{\lambda\, t} + c_2 \,e^{\lambda\, t} \left( t\,{\bf \xi} + {\bf \eta} \right) ,
\]
where \( {\bf \eta} \) is so called the generalized eigenvector. The phase portrait
shares characteristics with that of a node. With
only one eigenvector, it is a degenerated-looking node that is a cross
between a node and a spiral point (see case 4 below). The trajectories
either all diverge away from the critical point to infinite-distant away
(when \( \lambda >0 ,\) ) or all converge to the critical point (when \( \lambda <0 .\) This
type of critical point is called an improper node. It is asymptotically
stable if \( \lambda <0 ,\) unstable if \( \lambda >0 .\)
Case 4: Complex conjugate eigenvalues. When the real part λ is zero, the
trajectories neither converge to the critical point nor
move to infinite-distant away. Rather, they stay in constant, elliptical
(or, rarely, circular) orbits. This type of critical point is called a
center. It has a unique stability classification shared by no other:
stable (or neutrally stable).
When the real part λ is nonzero, the trajectories still retain the elliptical traces as in the previous case.
However, with each revolution, their distances from the critical point
grow/decay exponentially according to the term \( e^{\Re\lambda\,t} , \) where
\( \Re\lambda \) is the real part of the complax λ. Therefore, the
phase portrait shows trajectories that spiral away from the critical
point to infinite-distant away (when \( \Re\lambda >0 \) ). Or trajectories that spiral
toward, and converge to the critical point (when \( Re\lambda <0 \) ). This type of
critical point is called a spiral point. It is asymptotically stable if \( \lambda <0 ,\)
it is unstable if \( \Re\lambda >0 . \)
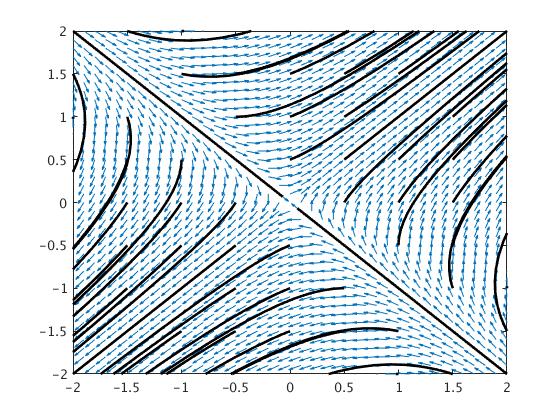
Example. Consider a system of ordinar differential equations
\[
\frac{{\text d}}{{\text d} t} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1&2 \\ 2&1 \end{bmatrix} \, \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} .
\]
The coefficient matrix
\( {\bf A} = \begin{bmatrix} 1&2 \\ 2&1 \end{bmatrix} \) has two distinct real eigenvalues
\( \lambda_1 =3 \) and
\( \lambda_2 =-1 . \) Therefore, the critical point, which is the origin, is a saddle point, unstable. We plot the corresponding phase portrait using the following code:
xgrid=-2:.1:2;
ygrid=-2:.1:2;
[X,Y]=meshgrid(xgrid,ygrid);
dxdt=X+2*Y;
dydt=2*X+Y;
r=sqrt(dxdt.^2+dydt.^2);
U=dxdt./r;
V=dydt./r;
figure
quiver(X,Y,U,V)
xlim([-2 2])
ylim([-2 2])
f=@(t,Y) [Y(1)+2*Y(2);2*Y(1)+Y(2)];
hold on
for alpha=-2:.5:2
for beta=-2:.5:2
x0=[alpha beta];
[t,x]=ode45(f,[0 2],x0);
plot(x(:,1),x(:,2), 'k','LineWidth',2)
end
end