Part 2.2: Motivation
This section presents motivating examples to study systems of ordinary differential equations (ODE for short),
In fact, the trajectory of any solution initiating in the first quadrant is contained in the first quadrant. So its global solution does not exist. ■

|

|
|
| Vertical trajectories. | Projectile thrown upward at angle α to abscissa. |
Its trajectory has a parabolic shape when the projectile of mass m is launched into a vacuum under angle α to horizontal axis (abscissa). The motionof the projectile is under the influence of gravity only. The position vector of the projectile at time t after firing is defined by the vector
- de Alwise, T., Projectile motion with Mathematica, International Journal of Mathematical Education in Science and Technology, 2000, Vol. 31, No. 5, pp.749--755. doe: 10.1080/002073900434413
- Benacka, I., Stubna, I., Ball launched against an inclined plane---an example of using recurrent sequences in school physics, International Journal of Mathematical Education in Science and Technology, 2009, Vol.40, No. 5, pp. 696--705.
- Bose, S.K., Thoughts on projectile motion, American Journal of Physics, 1985, Vol. 53, No. 2, pp. 175
- de Mestre, N., The Mathematics of Projectiles in Sport, Cambridge University Press, 2012, https://doi.org/10.1017/CBO9780511624032
- Donnelly, D., The parabolic envelope of constant initial speed trajectories, American Journal of Physics, 1992, Vol. 60, No. 12, pp. 1149--1150.
- Fernández-Chapou, J.L., Salas-Brito, A.L. and Vargas, C.A., An elliptic property of parabolic trajectories, American Journal of Physics, 2004, Vol. 72, pp. 1109--1110.
- Hu, H., Yu, J., Another look at Projectile motion, The Physics Teacher, 2000, Vol. 38, No. 10, page 423.
- Padyala, R., An alternative view of the elliptic property of a family of projectile paths, The Physics Teacher, 2019, Vol. 57, No. 9, pp376--377.
- Sarafian, H., On projectile motion, The Physics Teacher, 1999, Vol. 37, No. 2, [[. 86--88.
Since an accurate determination of the resistive force is very complicated, we concentrate our attention on a projectile having shape of a sphere. Fortunately, the dependents of the air resistive force acting on a ball is known and it depends on projectile's speed. For a sphere of radius r moving a fluid of density ρ and viscosity η, the drag force and the Reynolds number are
|
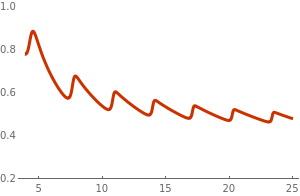
The dependence of the drag force on velocity of a ball moving in air is well documented. Experiments measuring drag force dependence on the ball velocity were conducted by the faculty at MIT, which shows a complicated behavior. For small velocities, it is approximately linear, but then drag force starts closer to the quadratic function with speed increases. At large Reynolds numbers, we observe turbulence behind the ball. So when speed increases (and the Reynolds number exceeds 105), the drag force declines and oscillates as shown in the figure. Such phenomena is observed in baseball and volleyball.
f[t_, y_] = Sin[2.35*t*y]*Cos[t + 1.0*y];;
s = NDSolve[{y'[t] == f[t, y[t]], y[0] == 1}, y, {t, 0, 30}]; Plot[Evaluate[y[t] /. s], {t, 3.9, 25}, PlotRange -> {0.2, 1}, PlotTheme -> "Web"] |
|
| Figure 1: Dependence of the drag force on ball's speed. | Mathematica code |
- The bob is free to move within a plane (so we consider only two-dimensional oscillations).
- The system is conservative, so the pendulum rotates in a vacuum and friction in the pivot is negligible.
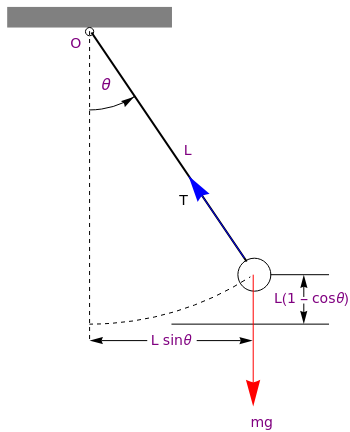
- The bob of mass m is attached to one end of a rigid, but weightless rod of length ℓ, which is assumed to be constant during the pendulum motion. The other end of the rod (or rigid spring) is supported at the pivot.
|
The modeling of the motion is greatly simplified when the given body (bob) is considered essentially as a point particle. The position of the bob is described by the angle θ between the rod and the downward equilibrium vertical position, with the counterclockwise direction taken as positive. The only force acting on the pendulum is the gravitational force m g, acting downward, where g denotes the acceleration due to gravity. The position of the bob can be determined in Cartesian coordinates as
\[
x = \ell \,\sin \theta , \qquad y = -\ell\,\cos\theta ,
\]
where the origin is taken at the pivot and the positive vertical direction is upward.
Using \( {\cal L} = \mbox{K} - \Pi , \) the
Lagrangian,
which is the difference of the kinetic energy K and the potential
energy Π of the system, we have
\[
\frac{\text d}{{\text d}t} \,\frac{\partial {\cal L}}{\partial \dot{\theta}}
= \frac{\partial {\cal L}}{\partial \theta} .
\]
|
With the kinetic energy expressed via the angular displacement θ
|
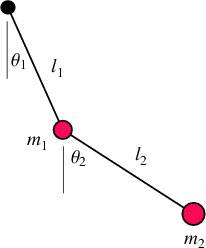
Now we consider a double pendulum, that consists of one pendulum attached to another. Consider a double bob pendulum with masses m1 and m2 attached by rigid massless wires of lengths ℓ1 and ℓ2. Further, let the angles the two wires make with the vertical be denoted θ1 and θ2, as illustrated in the figure to the left. Finally, let gravity acceleration be given by g. Then the positions of the bobs are given by
\begin{align*}
x_1 &= \ell_1 \sin\theta_1 , \\
y_1 &= - \ell_1 \cos\theta_1 , \\
x_2 &= \ell_1 \sin\theta_1 + \ell_2 \sin\theta_2 , \\
y_2 &= - \ell_1 \cos\theta_1 - \ell_2 \cos\theta_2 .
\end{align*}
|
The potential energy of the system is then given by
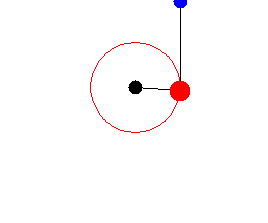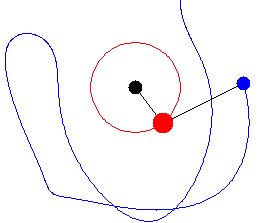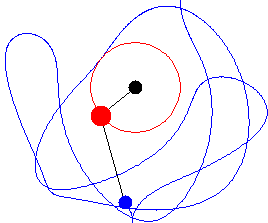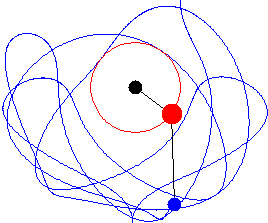
|
Similarly, for θ2:
\begin{align*}
\frac{\partial {\cal L}}{\partial \dot{\theta}_2} &= m_2 \ell_2^2 \dot{\theta}_2 + m_2 \ell_1 \ell_2 \cos \left( \theta_1 - \theta_2 \right) ,
\\
\frac{\text d}{{\text d}t} \left( \frac{\partial {\cal L}}{\partial \dot{\theta}_2} \right) &= m_2 \ell_2^2 \ddot{\theta}_2 + m_2 \ell_1 \ell_2 \ddot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) - m_2 \ell_1 \ell_2 \dot{\theta}_1 \sin \left( \theta_1 - \theta_2 \right) \left( \dot{\theta}_1 - \dot{\theta}_2 \right) ,
\\
\frac{\partial {\cal L}}{\partial \theta_2} &= m_2 \ell_1 \ell_2 \dot{\theta}_1 \dot{\theta}_2 \sin \left( \theta_1 - \theta_2 \right) - \ell_2 m_2 g \sin\theta_2 ,
\end{align*}
so the Euler-Lagrange differential equation \eqref{EqMotiv.2} for variable θ2becomes
|

|
polygon = Graphics[Polygon[{{-3, 0}, {3, 0}, {3, 1/4}, {-3, 1/4}}]];
line1 = Graphics[{Dashed, Line[{{2.5, 0}, {2.5, -5}}]}]; line2 = Graphics[{Dashed, Line[{{-2.5, 0}, {-2.5, -5}}]}]; line3 = Graphics[{Thickness[0.01], Line[{{2.5, 0}, {4.5, -3.6}}]}]; line4 = Graphics[{Thickness[0.01], Line[{{-2.5, 0}, {-3.9, -3.6}}]}]; circle1 = Graphics[Circle[{4.66, -4}, 0.38]]; circle2 = Graphics[Circle[{-4.0, -4}, 0.38]]; txt1 = Graphics[ Text[Style[Subscript[m, 1], FontSize -> 14, Purple], {-3.95, -4.0}]]; txt2 = Graphics[ Text[Style[Subscript[m, 2], FontSize -> 14, Purple], {4.68, -4.0}]]; spring = Graphics[{Thickness[0.01], Line[{{-3.35, -2.3}, {-1.7, -2.3}, {-1.5, -2.0}, {-1.5, -2.6}, \ {-1.0, -2.0}, {-1.0, -2.6}, {-0.5, -2}, {-0.5, -2.6}, {0, -2}, {0, \ -2.6}, {0.5, -2.0}, {0.5, -2.6}, {1, -2}, {1, -2.6}, {1.5, -2}, {1.5, \ -2.6}, {1.7, -2.3}, {3.69, -2.3}}]}]; txtk = Graphics[Text[Style["k", FontSize -> 18, Blue], {0.25, -1.4}]]; txt11 = Graphics[ Text[Style[Subscript[\[Theta], 1], FontSize -> 14, Purple], {-2.77, -1.8}]]; txt22 = Graphics[ Text[Style[Subscript[\[Theta], 2], FontSize -> 14, Purple], {2.98, -1.8}]]; Show[polygon, line1, line2, line3, line4, circle1, circle2, txt1, \ txt2, spring, txtk, txt11, txt22] |
|
| Two pendula. | Mathematica code |
Substituting these expressions into the Euler--Lagrange equations \eqref{EqMotiv.2}, we obtain the system of motion:
We consider a situation when two bodies of masses m1 and m2 that are connected to three springs of negligible mass having spring constants k1 k2, and k3, respectively. We denote by x1 and x2 displacement of each body from its equilibrium position.

|
mass1 = Graphics[{Thickness[0.01],
Line[{{-12.5, 0.5}, {-2.5, 0.5}, {-2.5, 4.5}, {-12.5, 4.5}, {-12.5,
0.5}}]}, Ticks -> None, Axes -> False];
mass2 = Graphics[{Thickness[0.01], Line[{{2.5, 0.5}, {2.5, 4.5}, {10.5, 4.5}, {10.5, 0.5}, {2.5, 0.5}}]}, Ticks -> None, Axes -> False]; spring1 = Graphics[{Thickness[0.005], Line[{{-12.5, 2.5}, {-14, 2.5}, {-14.4, 1.5}, {-14.8, 3.5}, {-15.2, 1.5}, {-15.6, 3.5}, {-16, 1.5}, {-16.4, 3.5}, {-16.6, 2.5}, {-17.5, 2.5}}]}, Ticks -> None, Axes -> False]; spring2 = Graphics[{Thickness[0.005], Line[{{-2.5, 2.5}, {-1.5, 2.5}, {-1, 1.5}, {-0.5, 3.5}, {0, 1.5}, {0.5, 3.5}, {1, 1.5}, {1.5, 3.5}, {2, 2.5}, {2.5, 2.5}}]}, Ticks -> None, Axes -> False]; spring3 = Graphics[{Thickness[0.005], Line[{{10.5, 2.5}, {11.5, 2.5}, {12, 1.5}, {12.5, 3.5}, {13, 1.5}, {13.5, 3.5}, {14, 1.5}, {14.5, 3.5}, {15, 2.5}, {16.5, 2.5}}]}, Ticks -> None, Axes -> False]; c1 = Graphics[{Thickness[0.01], Circle[{-10, 0}, 0.5]}]; c2 = Graphics[{Thickness[0.01], Circle[{-5, 0}, 0.5]}]; c3 = Graphics[{Thickness[0.01], Circle[{5, 0}, 0.5]}]; c4 = Graphics[{Thickness[0.01], Circle[{8, 0}, 0.5]}]; polygon = Graphics[{LightGray, Polygon[{{-17.5, -0.5}, {16.5, -0.5}, {16.5, -2.5}, {-17.5, -2.5}}]}]; poly1 = Graphics[{LightGray, Polygon[{{-17.5, -2.5}, {-18, -2.5}, {-18, 5}, {-17.5, 5}}]}];; poly2 = Graphics[{LightGray, Polygon[{{16.5, -2.5}, {18, -2.5}, {18, 5}, {16.5, 5}}]}]; l1 = Graphics[{Dashed, Line[{{-12.5, 4.5}, {-12.5, 6.5}}]}]; l2 = Graphics[{Dashed, Line[{{2.5, 4.5}, {2.5, 6.5}}]}]; a1 = Graphics[Arrow[{{-12.5, 6}, {-8, 6}}]]; a2 = Graphics[Arrow[{{2.5, 6}, {7, 6}}]]; txt1 = Graphics[ Text[Style[Subscript[x, 1], FontSize -> 14, Purple], {-7, 6}]]; txt2 = Graphics[ Text[Style[Subscript[x, 2], FontSize -> 14, Purple], {8, 6}]]; t1 = Graphics[ Text[Style[Subscript[m, 1], FontSize -> 18, Purple], {-7, 2.5}]]; t2 = Graphics[ Text[Style[Subscript[m, 2], FontSize -> 18, Purple], {7, 2.5}]]; k1 = Graphics[ Text[Style[Subscript[k, 1], FontSize -> 14, Purple], {-15, 5}]]; k2 = Graphics[ Text[Style[Subscript[k, 2], FontSize -> 14, Purple], {0, 5}]]; k3 = Graphics[ Text[Style[Subscript[k, 3], FontSize -> 14, Purple], {13.5, 5}]]; Show[mass1, mass2, spring1, spring2, spring3, c1, c2, c3, c4, polygon, poly1, poly2, l1, l2, a1, a2, txt1, txt2,t1,t2,k1,k2,k3] |
|
| Spring-mass system. | Mathematica code |
This example can be used to model several mechanical systems because there are many situations when we observe masses connected with each other. For example, a multi-store building can be considered as masses (corresponding to each floor) connecting with springs. You can model an entire set of automobiles with several hundred masses connected to each other by several undred springs and can analyze how each part of the whole car vibrates when you drive this caravan along a bumpy road. Or you can model an entire set of rail cars with several masses, one for each car and one for the locomotive, all connected to each other by several springs and then analyze how each part of the whole train vibrates when the train chugs along climbing the mountain rail. You may think this kind of simple two mass and three spring model is not adequate to complicated models from real life, but in reality the logic and process of modeling is exactly the same. You would just have several dozens of differential equations instead of two or three equations, which is very similar to what you see here.
Let x1 and x2 be displacements of masses m1 and m2, respectively, from their equilibrium positions. So we consider these variables as canonical coordinates. Then the kinetic energy of these two objects will be

|
coil = ParametricPlot[{1*Cos[t*3 + Pi] + 1.5*t - 9,
2*Sin[t*3] - 8}, {t, 0, 5*Pi}, PlotLabel -> "L", Ticks -> None,
Axes -> False, ImageSize -> Tiny, PlotStyle -> {Thickness[0.01]}];
resistor2 = Graphics[{Thickness[0.01], Line[{{-15, -8}, {-15, -2}, {-17, 0}, {-13, 0}, {-17, 2}, {-13, 2}, {-17, 4}, {-13, 4}, {-17, 6}, {-13, 6}, {-17, 8}, {-13, 8}, {-15, 9}, {-15, 11}}]}, PlotLabel -> Subscript[R, 1], Ticks -> None, Axes -> False]; resistor1 = Graphics[{Thickness[0.01], Line[{{15.5619, -8}, {18, -8}, {18, -2}, {20, 0}, {16, 0}, {20, 2}, {16, 2}, {20, 4}, {16, 4}, {20, 6}, {16, 6}, {20, 8}, {16, 8}, {18, 9}, {18, 11}}]}, PlotLabel -> Subscript[R, 1], Ticks -> None, Axes -> False]; c1 = Graphics[{Thickness[0.01], Circle[{-30, 2}, 2]}]; l1 = Graphics[{Thickness[0.008], Line[{{-25.4, 9.5}, {-25.4, 12.5}}]}]; l2 = Graphics[{Thickness[0.008], Line[{{-24.6, 9.5}, {-24.6, 12.5}}]}]; l3 = Graphics[{Thickness[0.01], Line[{{-10, -8}, {-30, -8}, {-30, 0}}]}]; l4 = Graphics[{Thickness[0.01], Line[{{-30, 4}, {-30, 11}, {-25.4, 11}}]}]; l5 = Graphics[{Thickness[0.01], Line[{{-24.6, 11}, {18, 11}}]}]; txtC = Graphics[ Text[Style["C", Bold, FontSize -> 14, Blue], {-25.5, 8.0}]]; txtV = Graphics[ Text[Style["V(t)", Bold, FontSize -> 14, Blue], {-25.5, 2.0}]]; txtL = Graphics[ Text[Style["L", Bold, FontSize -> 14, Blue], {2.0, -4.5}]]; txtR1 = Graphics[ Text[Style[Subscript[R, 1], Bold, FontSize -> 14, Blue], {-10.5, 2.5}]]; txtR2 = Graphics[ Text[Style[Subscript[R, 2], Bold, FontSize -> 14, Blue], {12.5, 2.5}]]; Show[l1, l2, l3, l4, l5, coil, resistor1, resistor2, c1, txtC, txtV, \ txtL, txtR1, txtR2] |
|
| Two-loop circuit. | Mathematica code |
We denote the current flowing through the left-hand loop by I1 and the current in the right-hand loop by I2 (both in the clockwise direction). The current through the resistor R1 is I1 − I2. The voltage drops on each element are
Now we consider another electric circuit with three loops.
To mathematically model the interplay of a married couple, let x(t) denote a measure of the husband's positivity (e.g., happiness) and let y(t) be the corresponding measurement for the wife's positivity (particular numerical values for such measurements can be found in John's work). In the absence of marital interaction, a single person tends to her/his own ``uninfluenced steady state:'' x0 and y0. This process is modeled by \[ \frac{{\text d}x}{{\text d}t} = h (x-x_0 ) , \qquad \frac{{\text d}y}{{\text d}t} = w (y-y_0 ) . \] After marriage, their interaction can be modeled as \begin{equation} \label{E511.m1} \frac{{\text d}x}{{\text d}t} = h (x-x_0 ) + I_1 (y) , \qquad \frac{{\text d}y}{{\text d}t} = w (y-y_0 ) + I_2 (x), \end{equation} where I1(y) is the influence exerted by the wife on the husband and I2(x) is the influence exerted by the husband on the wife. In a validating style of interaction, these functions can be modeled by \begin{equation} \label{E511.m2} I_k (z) = \begin{cases} a_k z , & \ \mbox{if } z>0 , \\ b_k z , & \ \mbox{if } z<0 \end{cases} \qquad (k=1,2). \end{equation} In a conflict avoiding style of interaction, the spouse who adopts this style avoids interacting with the other spouse through the negative range of his/her emotions. The corresponding function I(z) can be chosen as I(z) = H(z), where H(t) is the Heaviside function. ■
Romeo is in love with Juliet, but in our version of this story, Juliet is a fickle lover. The more Romeo loves her, the more Juliet wants to run away and hide. But when Romeo gets discouraged and backs off, Juliet begins to find him strangely attractive. Romeo, on the other hand, tends to echo her: he warms up when she loves him, and grows cold when she hates him.
Let us introduce variables