Linear Systems of Algebraic Equations
This page presents some topics from Linear Algebra needed for construction of solutions to systems of linear algebraic equations and some applications. We use matrices and vectors as essential elements in obtaining and expressing the solutions.
Matrices and Vectors
The central problem of linear algebra is to solve a linear system of equations. This means that the unknowns are only multiplied by numbers.
Our first example of a linear system has two equations in two unknowns:
\[
\begin{cases}
x-3y &= -1 , \\
2x+y &=5 .
\end{cases}
\]
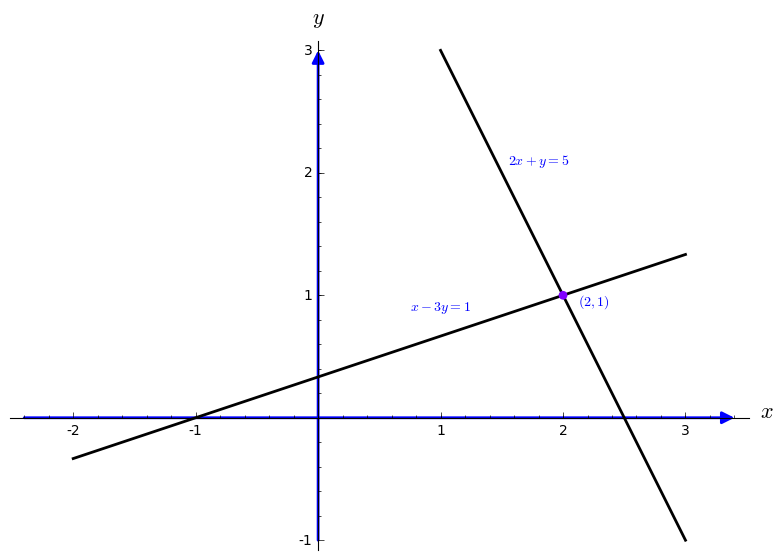
We begin with a row at a time. The first equation \( x-3y=-1 \) produces a straight line in the
\( xy- \) plane. The second equation \( 2x+y=5 \) defines another
line. By plotting these two lines, you cannot miss the intersection point where two lines meet. The point
\( x=2, \ y=1 \) lies on both lines. That point solves both equations at once.
Now we visualize this with a picture:
sage: l1=line([(-2,-1/3), (3,4/3)],thickness=2,color="black")
sage: l2=line([(1,3), (3,-1)],thickness=2,color="black")
sage: ah = arrow((-2.4,0), (3.4,0))
sage: av = arrow((0,-1), (0,3))
sage: P=circle((2.0,1.0),0.03, rgbcolor=hue(0.75), fill=True)
sage: t1=text(r"$(2,1)$",(2.25,0.95))
sage: t2=text(r"$x-3y=1$",(1.0,0.9))
sage: t2=text(r"$x-3y=1$",(1.0,0.9))
sage: t3=text(r"$2x+y=5$",(1.8,2.1))
sage: show(l1+l2+ah+av+t1+t2+t3+P,axes_labels=['$x$','$y$'])
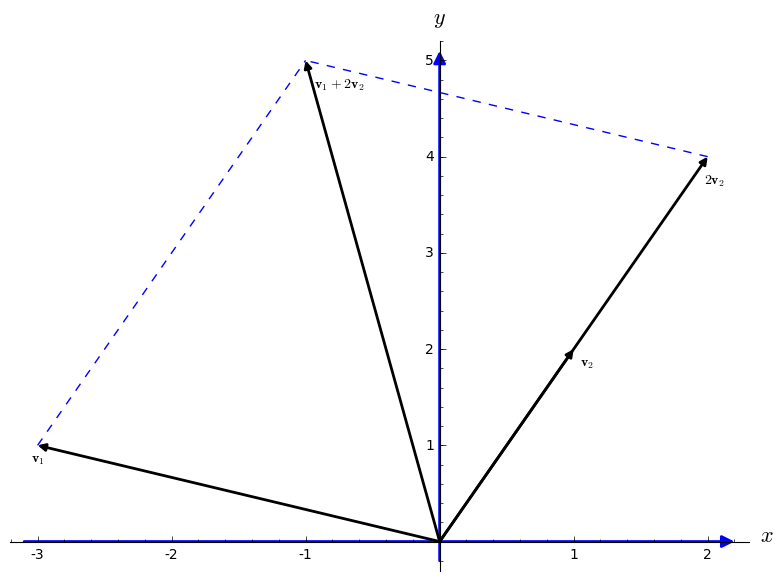
Now we plot another graph:
sage: ah = arrow((-3.1,0), (2.2,0))
sage: av = arrow((0,-0.2), (0,5.1))
sage: a1=arrow([0,0],[-3,1], width=2, arrowsize=3,color="black")
sage: a2=arrow([0,0],[1,2], width=2, arrowsize=3,color="black")
sage: a3=arrow([0,0],[2,4], width=2, arrowsize=3,color="black")
sage: a4=arrow([0,0],[-1,5], width=2, arrowsize=3,color="black")
sage: l1=line([(-3,1), (-1,5)],color="blue",linestyle="dashed")
sage: l2=line([(2,4), (-1,5)],color="blue",linestyle="dashed")
sage: t1=text(r"${\bf v}_1$",(-3,0.85),color="black")
sage: t2=text(r"${\bf v}_2$",(1.1,1.85),color="black")
sage: t3=text(r"$2{\bf v}_2$",(2.05,3.75),color="black")
sage: t4=text(r"${\bf v}_1 + 2{\bf v}_2$",(-0.75,4.75),color="black")
sage: show(av+ah+a1+a2+a3+a4+l1+l2+t1+t2+t3+t4,axes_labels=['$x$','$y$'])
The row picture shows that two lines meet at a single point. Then we turn to the column picture by rewriting the system in vector form:
\[
x \begin{bmatrix}
1 \\
2
\end{bmatrix} + y \begin{bmatrix}
-3 \\
1
\end{bmatrix} = \begin{bmatrix}
-1 \\
5
\end{bmatrix} = {\bf b} .
\]
This has two columns on the left.
The problem is to find the combination of those vectors that equals the vector on the right.
We are multiplying the first column by \( x \) and the second by \( y ,\) and adding.
The figure at the right illustrates two basic operations with vectors: scalar multiplication and vector addition. With these two operations, we are able to build linear combination of vectors:
\[
2 \begin{bmatrix}
1 \\
2
\end{bmatrix} + 1 \begin{bmatrix}
-3 \\
1
\end{bmatrix} = \begin{bmatrix}
-1 \\
5
\end{bmatrix} .
\]
The
coefficient matrix on the left side of the equations is 2 by 2 matrix
A:
\[
{\bf A} = \begin{bmatrix}
1 & -3 \\
2 & 1
\end{bmatrix} .
\]
This allows us to rewrite the given system of linear equations in vector form (also sometimes called the matrix form, but we reserve the matrix form for matrix equations)
\[
{\bf A} \, {\bf x} = {\bf b} ,\qquad\mbox{which is }\quad \begin{bmatrix}
1 & -3 \\
2 & 1
\end{bmatrix} \, \begin{bmatrix}
x \\
y
\end{bmatrix} = \begin{bmatrix}
-1 \\
5
\end{bmatrix} .
\]
We use the above linear equation to demonstrate a great technique, called elimination. Before elimination,
\( x \)
and
\( y \) appear in both equations. After elimination, the first unknown
\( x \)
has disappeared from the second equation:
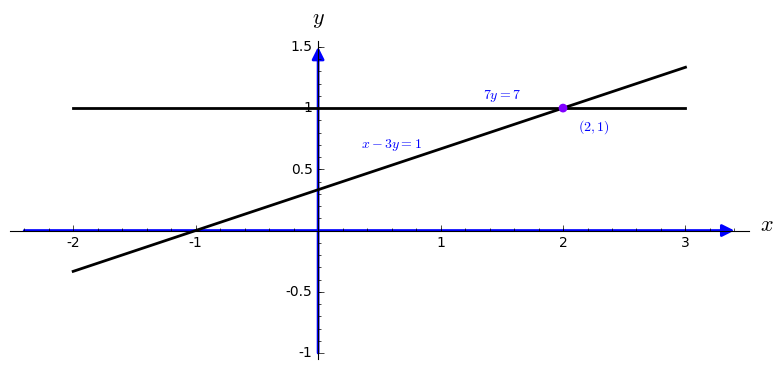
\[
{\bf Before: }\quad \begin{cases} x-3y &= -1 , \\
2x+y &=5 .
\end{cases} \qquad {\bf After: } \quad \begin{cases} x-3y &= -1 , \\
7\,y &=7
\end{cases} \qquad \begin{array}{l} \mbox{(multiply by 2 and subtract)} \\
(x \mbox{ has been eliminated).}
\end{array}
\]
The last equation
\( 7\,y =7 \) instantly gives
\( y=1. \) Substituting for
\( y \) in the first equation leaves
\( x -3 = -1. \) Therefore,
\( x=2 \) and the solution
\( (x,y) =(2,1) \) is complete.
sage: l1=line([(-2,-1/3), (3,4/3)],thickness=2,color="black")
sage: l2=line([(-2,1), (3,1)],thickness=2,color="black")
sage: ah = arrow((-2.4,0), (3.4,0))
sage: av = arrow((0,-1), (0,1.5))
sage: P=circle((2.0,1.0),0.03, rgbcolor=hue(0.75), fill=True)
sage: t1=text(r"$(2,1)$",(2.25,0.85))
sage: t2=text(r"$x-3y=1$",(0.6,0.7))
sage: t3=text(r"$7y=7$",(1.5,1.1))
sage: show(l1+l2+ah+av+t1+t2+t3+P,axes_labels=['$x$','$y$'])
Sage solves linear systems
A system of
\( m \) equations in
\( n \) unknowns
\( x_1 , \ x_2 , \ \ldots , \ x_n \) is a set of
\( m \) equations of the form
\[
\begin{cases}
a_{11} \,x_1 + a_{12}\, x_2 + \cdots + a_{1n}\, x_n &= b_1 ,
\\
a_{21} \,x_1 + a_{22}\, x_2 + \cdots + a_{2n}\, x_n &= b_2 ,
\\
\qquad \vdots & \qquad \vdots
\\
a_{m1} \,x_1 + a_{m2}\, x_2 + \cdots + a_{mn}\, x_n &= b_n ,
\end{cases}
\]
The numbers
\( a_{ij} \) are known as the
coefficients of the system. The matrix
\( {\bf A} = [\,a_{ij}\,] , \) whose
\( (i,\, j) \) entry is the
coefficient
\( a_{ij} \) of the system of linear equations is called the coefficient matrix and is denoted by
\[
{\bf A} = \left[ \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{array} \right] \qquad\mbox{or} \qquad {\bf A} = \left( \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{array} \right) .
\]
Let
\( {\bf x} =\left[ x_1 , x_2 , \ldots x_n \right]^T \) be the vector of unknowns. Then the product
\( {\bf A}\,{\bf x} \) of the
\( m \times n \) coefficient matrix
A and the
\( n \times 1 \) column vector
x is an
\( m \times 1 \) matrix
\[
\left[ \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{array} \right] \, \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}
= \begin{bmatrix} a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n
\\ a_{2,1} x_1 + a_{2,2} x_2 + \cdots + a_{2,n} x_n \\ \vdots \\ a_{m,1} x_1 + a_{m,2} x_2 + \cdots + a_{m,n} x_n \end{bmatrix} ,
\]
whose entries are the right-hand sides of our system of linear equations.
If we define another column vector \( {\bf b} = \left[ b_1 , b_2 , \ldots b_m \right]^T \)
whose components are the right-hand sides \( b_{i} ,\) the system is equivalent to the vector equation
\[
{\bf A} \, {\bf x} = {\bf b} .
\]
We say that \( s_1 , \ s_2 , \ \ldots , \ s_n \) is a solution of the system if all
\( m \) equations hold true when
\[
x_1 = s_1 , \ x_2 = s_2 , \ \ldots , \ x_n = s_n .
\]
Sometimes a system of linear equations is known as a set of simultaneous equations; such terminology emphasises that a solution is an assignment of values to each of the
\( n \) unknowns such that each and every equation holds with this assignment. It is also referred to simply as a linear system.
Example. The linear system
\[
\begin{cases}
x_1 + x_2 + x_3 + x_4 + x_5 &= 3 ,
\\
2\,x_1 + x_2 + x_3 + x_4 + 2\, x_5 &= 4 ,
\\
x_1 - x_2 - x_3 + x_4 + x_5 &= 5 ,
\\
x_1 + x_4 + x_5 &= 4 ,
\end{cases}
\]
is an example of a system of four equations in five unknowns,
\( x_1 , \ x_2 , \ x_3 , \ x_4 , \ x_5 . \)
One solution of this system is
\[
x_1 = -1 , \ x_2 = -2 , \ x_3 =1, \ x_4 = 3 , \ x_5 = 2 ,
\]
as you can easily verify by substituting these values into the equations. Every equation is satisfied for these values of
\( x_1 , \ x_2 , \ x_3 , \ x_4 , \ x_5 . \)
However, there is not the only solution to this system of equations. There are many others.
On the other hand, the system of linear equations
\[
\begin{cases}
x_1 + x_2 + x_3 + x_4 + x_5 &= 3 ,
\\
2\,x_1 + x_2 + x_3 + x_4 + 2\, x_5 &= 4 ,
\\
x_1 - x_2 - x_3 + x_4 + x_5 &= 5 ,
\\
x_1 + x_4 + x_5 &= 6 ,
\end{cases}
\]
has no solution. There are no numbers we can assign to the unknowns
\( x_1 , \ x_2 , \ x_3 , \ x_4 , \ x_5 \) so that all four equations are satisfied. ■
In general, we say that a linear system of algebraic equations is consistent if it has at least one solution and inconsistent if it has no solution. Thus, a consistent linear system has either one solution or infinitely many solutions---there are no other possibilities.
Theorem: Let A be an \( m \times n \) matrix.
-
(Overdetermined case) If m > n, then the linear system \( {\bf A}\,{\bf x} = {\bf b} \)
is inconsistent for at least one vector b in \( \mathbb{R}^n . \)
- (Underdetermined case) If m < n, then for each vector b in \( \mathbb{R}^m \)
the linear system \( {\bf A}\,{\bf x} = {\bf b} \) is either inconsistent or has infinite many solutions. ■
Theorem: If A is an \( m \times n \) matrix with
\( m < n, \) then \( {\bf A}\,{\bf x} = {\bf 0} \) has
infinitely many solutions. ■
Theorem: A system of linear equations \( {\bf A}\,{\bf x} = {\bf b} \) is consistent if and only if b is in the column space of A. ■
Theorem: A linear system of algebraic equations \( {\bf A}\,{\bf x} = {\bf b} \) is consistent if and only if the vector b is orthogonal
to every solution y of the adjoint homogeneous equation \( {\bf A}^T \,{\bf y} = {\bf 0} \) or \( {\bf y}^T {\bf A} = {\bf 0} . \) ■
Sage uses standard commands to solve linear systems of algebraic equations:
\[
{\bf A} \, {\bf x} = {\bf b} , \qquad {\bf A} = \left[ \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{array} \right] , \quad {\bf x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} , \qquad
{\bf b} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix} .
\]
Here b is a given vector and column-vector x is to be determined. An augmented matrix is a matrix
obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.
We associate with the given system of linear equations \( {\bf A}\,{\bf x} = {\bf b} \) an augmented matrix by appending the column-vector b to the matrix A.
Such matrix is denoted by \( {\bf M} = \left( {\bf A}\,\vert \,{\bf b} \right) \) or \( {\bf M} = \left[ {\bf A}\,\vert \,{\bf b} \right] : \)
\[
{\bf M} = \left( {\bf A}\,\vert \,{\bf b} \right) = \left[ {\bf A}\,\vert \,{\bf b} \right] =
\left[ \begin{array}{cccc|c} a_{1,1} & a_{1,2} & \cdots & a_{1,n} & b_1 \\
a_{2,1} & a_{2,2} & \cdots & a_{2,n} & b_2 \\
\vdots & \vdots & \ddots & \vdots & \vdots\\
a_{m,1} & a_{m,2} & \cdots & a_{m,n} & b_m \end{array} \right] .
\]
Theorem: Let A be an \( m \times n \) matrix. A linear system of equations
\( {\bf A}\,{\bf x} = {\bf b} \) is consistent if and only if the rank of the coefficient matrice A is the same as the rank of the augmented matrix \( \left[ {\bf A}\,\vert \, {\bf b} \right] . \) ■
The actual use of the term augmented matrix appears to have been introduced by the American mathematician Maxime Bocher (1867--1918) in 1907.
We show how it works by examples. The system can be solved using solve command
sage: solve([eq1==0,eq2==0],x1,x2)
However, this is somewhat complex and we use vector approach:
sage: A = Matrix([[1,2,3],[3,2,1],[1,1,1]])
sage: b = vector([0, -4, -1])
sage: x = A.solve_right(b)
sage: x
(-2, 1, 0)
sage: A * x # checking our answer...
(0, -4, -1)
A backslash \ can be used in the place of solve_right; use
A \ b instead of A.solve_right(b).
If there is no solution, Sage returns an error:
sage: A.solve_right(w)
Traceback (most recent call last):
...
ValueError: matrix equation has no solutions
Similarly, use A.solve_left(b) to solve for x in
\( {\bf x}\, {\bf A} = {\bf b}\).
If a square matrix is nonsingular (invertible), then solutions of the vector equation \( {\bf A}\,{\bf x} = {\bf b} \)
can be obtained by applying the inverse matrix:
\( {\bf x} = {\bf A}^{-1} {\bf b} . \) We will discuss this method later in the section devoted to inverse matrices.
Elementary Row Operations
Our objective is to find an efficient method of finding the solutions of systems of linear equations. There are three operations that we can perform on the equations of a linear system without altering the set of solutions:
- multiply both sides of an equation by a non-zero constant;
- interchange two equations;
- add a multiple of one equation to another.
These operations, usually called elementary row operations, do not alter the set of solutions of the linear system
\( {\bf A}\,{\bf x} = {\bf b} \) since the restrictions on the variables
\( x_1 , \, x_2 , \, \ldots , \,x_n \) given by the new equations imply the restrictions given by the old ones. At the same time,
these operations really only involve the coefficients of the variables and the right-hand sides of the equations,
b.
Since the coefficient matrix A together with the given constant vector b contains all the information we need to use, we unite them into one matrix, called the augmented matrix:
\[
{\bf M} = \left( {\bf A}\,\vert \,{\bf b} \right) \qquad \mbox{or} \qquad {\bf M} = \left[ {\bf A}\,\vert \,{\bf b} \right] .
\]
Now rather than manipulating the equations, we can instead manipulate the rows of this augmented matrix. These observations form the motivation behind a method to solve systems of linear equations, known as Gaussian elimination, called after its inventor Carl Friedrich Gauss (1777--1855) from Germany.
Various modifications have been made to the method of elimination, and we present one of these, known as the Gauss--Jordan method.
It was the German geodesist Wilhelm Jordan
(1842-1899) and not a French mathematician Camille Jordan (1838-1922) who introduced the Gauss-Jordan method of solving systems of linear equations. Camille Jordan is credited for Jordan normal form, a
well known linear algebra topic.
Elimination produces an upper triangular system, called row echelon form for Gauss elimination and reduced row echelon form for Gauss--Jordan algorithm. The Gauss elimination introduces zeroes below the pivots, while Gauss--Jordan algorithm contains additional phase in which it introduces zeroes above the pivots.
Since this phase involves roughly 50% more operations than Gaussian elimination, most computer algorithms are based on the latter method.
Suppose M is the augmented matrix of a linear system. We can solve the linear
system by performing elementary row operations on M. In Sage these row operations
are implemented with the functions.
sage: M.swap_rows() # interchange two rows
sage: rescale_row() # scale a row by using a scale factor
sage: add_multiple_of_row() # add a multiple of one row to another row, replacing the row
Remember, row numbering starts at 0. Pay careful attention to the changes made to
the matrix by each of the following commands.
We want to start with a 1 in the first position of the first column, so we begin
by scaling the first row by 1/2.
sage: M.rescale_row(0,1/2); M
The first argument to rescale_row() is the index of the row to be scaled and the
second argument is the scale factor. We could, of course, use 0.5 rather than
1/2 for the scale factor.
Now that there is a 1 in the first position of the first column we continue by
eliminating the entry below it.
sage: M.add_multiple_of_row(1,0,1); M
The first argument is the index of the row to be replaced, the second argument is
the row to form a multiple of, and the final argument is the scale factor. Thus,
M.add_multiple_of_row(n,m,a) would replace row n with (row n)+a*(row m).
Since the last entry in the first column is already zero we can move on to the
second column. Our first step is to get a 1 in the second position of the second
column. Normally we would do this by scaling the row but in this case we can swap
the second and third row
sage: M.swap_rows(1,2); M
The arguments to swap_rows() are fairly obvious, just remember that row 1 is the
second row and row 2 is the third row.
Now we want to eliminate the 5 below the 1. This is done by multiplying the second
row by −5 and adding it to the third row.
sage: M.add_multiple_of_row(2,1,-5); M
To get a 1 as the last entry in the third column we can scale the third row by −1/2
sage: M.rescale_row(2,-1/2); M
At this point, the matrix is in echelon form (well, having the 1's down the diagonal
of the matrix is not required, but it does make our work easier). All that remains
to find the solution is to put the matrix in reduced echelon form which requires
that we replace all entries in the first three columns that are not on the main
diagonal (where the 1's are) with zeros. We will start with the third column and
work our way up and to the left. Remember that this is an augmented matrix and we
are going to ignore the right-most column; it just "goes along for the ride."
sage: M.add_multiple_of_row(1,2,-1); M
sage: M.add_multiple_of_row(0,1,-2); M
Therefore, our solution is complete. We see that the solution to our linear
system is
\( x_1 =2, \ x_2 =1, \ \mbox{and} \ x_3 =-1 . \)
There is an easy way to check your work, or to carry out these steps in the future.
First, let's reload the matrix M.
sage: M=matrix(QQ,[[2,4,0,8],[-1,3,3,-2],[0,1,1,0]]); M
The function echelon_form() will display the echelon form of a matrix without
changing the matrix.
Notice that the matrix
M is unchanged.
To replace
M with its reduced echelon form, use the echelonize() function.
Sage has the matrix method .pivot()
to quickly and easily identify the pivot columns
of the reduced row-echelon form of a matrix. Notice that we do not have to row-
reduce the matrix first, we just ask which columns of a matrix
A would be
the pivot columns of the matrix
B that is row-equivalent to
A and in reduced row-echelon form.
By definition, the indices of the pivot columns for an augmented matrix of a
system of equations are the indices of the dependent variables. And the remainder
are free variables. But be careful, Sage numbers columns starting from zero and
mathematicians typically number variables starting from one.
sage: coeff = matrix(QQ, [[ 1, 4, 0, -1, 0, 7, -9],
... [ 2, 8,-1, 3, 9, -13, 7],
... [ 0, 0, 2, -3, -4, 12, -8],
... [-1, -4, 2, 4, 8, -31, 37]])
sage: const = vector(QQ, [3, 9, 1, 4])
sage: aug = coeff.augment(const),
sage: dependent = aug.pivots()
sage: dependent
(0, 2, 3)
So, incrementing each column index by 1 gives us the same set D
of indices for the
dependent variables. To get the free variables, we can use the following code. Study
it and then read the explanation following.
sage: free = [index for index in range(7) if not index in dependent]
sage: free
[1, 4, 5, 6]
This is a Python programming construction known as a “list comprehension” but
in this setting I prefer to call it “set builder notation.” Let’s dissect the command
in pieces. The brackets ([,]) create a new list. The items in the list will be values
of the variable index .range(7) is another list, integers starting at 0
and stopping justbefore 7. (While perhaps a bit odd, this works very well when we consistently
start counting at zero.) So range(7) is the list
[0,1,2,3,4,5,6]. Think of these as
candidate values for index, which are generated by for index in range(7). Then
we test each candidate, and keep it in the new list if it is
not in the list dependent. This is entirely analogous to the following mathematics:
\[
F= \{ f \, \vert \, 1 \le f \le 7, \ f \not\in D \} ,
\]
where
F is free,
f is index, and
D is dependent, and we make the 0/1 counting
adjustments. This ability to construct sets in Sage with notation so closely mirroring
the mathematics is a powerful feature worth mastering. We will use it repeatedly. It
was a good exercise to use a list comprehension to form the list of columns that are
not pivot columns. However, Sage has us covered.
sage: free_and_easy = coeff.nonpivots()
sage: free_and_easy
[1, 4, 5, 6]
Example.
We illustrate how to find an inverse matrix using row operations. Consider the matrix
\[
{\bf A} = \left[ \begin{array}{ccc} 1& 2 & 3 \\ 2&5&3 \\ 1&0 & 8 \end{array} \right] .
\]
To accomplish this goal, we add a block of the identity matrix and apply row operation to this augmented matrix
\( \left[ {\bf A} \,| \,{\bf I} \right] \) until the left side is reduced to
I.
These operatioons will convert the right side to
\( {\bf A}^{-1} ,\) so the final matrix will have the form
\( \left[ {\bf I} \,| \,{\bf A}^{-1} \right] .\)
\begin{align*}
\left[ {\bf A} \,| \,{\bf I} \right] &= \left[ \begin{array}{ccc|ccc} 1& 2 & 3 & 1&0&0 \\ 2&5&3 & 0&1&0 \\ 1&0 & 8 & 0&0&1 \end{array} \right]
\\
&= \left[ \begin{array}{ccc|ccc} 1& 2 & 3 & 1&0&0 \\ 0&1&-3 & -2&1&0 \\ 0&-2 &5 & -1&0&1 \end{array} \right] \qquad
\begin{array}{l} \mbox{add $-2$ times the first row to the second} \\ \mbox{and $-1$ times the first row to the third} \end{array}
\\
&= \left[ \begin{array}{ccc|ccc} 1& 2 & 3 & 1&0&0 \\ 0&1&-3 & -2&1&0 \\ 0&0 &-1 & -5&2&1 \end{array} \right] \qquad
\begin{array}{l} \mbox{add 2 times the second row to the third} \end{array}
\\
&= \left[ \begin{array}{ccc|ccc} 1& 2 & 3 & 1&0&0 \\ 0&1&-3 & -2&1&0 \\ 0&0 &1 & 5&-2&-1 \end{array} \right] \qquad
\begin{array}{l} \mbox{multiply the third row by $-1$} \end{array}
\\
&= \left[ \begin{array}{ccc|ccc} 1& 2 & 0 & -14&6&3 \\ 0&1&0 & 13&-5&-3 \\ 0&0&1 & 5&-2&-1 \end{array} \right] \qquad
\begin{array}{l} \mbox{add 3 times the third row to the second} \\ \mbox{and $-3$ times the third row to the first} \end{array}
\\
&= \left[ \begin{array}{ccc|ccc} 1& 0 & 0 & -40&16&9 \\ 0&1&0 & 13&-5&-3 \\ 0&0 &1 & 5&-2&-1 \end{array} \right] \qquad
\begin{array}{l} \mbox{add $-2$ times the second row to the first} \end{array} .
\end{align*}
Thus,
\[
{\bf A}^{-1} = \left[ \begin{array}{ccc} -40& 16 & 9 \\ 13&-5&-3 \\ 5&-2 &-1 \end{array} \right] .
\]
Row Echelon Forms
In previous section, we demonstrate how Gauss elimination procedure is applied to a matrix, row by row, in order to obtain row echelon form.
Specifically, a matrix is in row echelon form if
- all nonzero rows (rows with at least one nonzero element) are above any rows of all zeroes (all zero rows, if any, belong at the bottom of the matrix), and
-
the leading coefficient (the first nonzero number from the left, also called the pivot) of a nonzero row is always strictly to the right of the leading coefficient
of the row above it (some texts add the condition that the leading coefficient must be 1 but it is not necessarily).
These two conditions imply that all entries in a column below a leading coefficient are zeroes.
Unlike the row echelon form, the reduced row echelon form of a matrix is unique and
does not depend on the algorithm used to compute it. It is obtained by applying the Gauss-Jordan elimination procedure.
A matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions:
- It is in row echelon form.
-
Every leading coefficient is 1 and is the only nonzero entry in its column.
Gauss elimination algorithm can be generalized for block matrices. Suppose that a \( (m+n) \times (m+n) \) matrix M is
partitioned into 2-by-2 blocks \( {\bf M} = \begin{bmatrix} {\bf A} & {\bf B} \\ {\bf C} & {\bf D} \end{bmatrix} .\)
When we apply Gauss elimination algorithm, A is just an entry (not zero) in upper left corner (which is 1 by 1 matrix). and
C is the column-vector (\( (m+n-1) \times 1 \) matrix). To eliminate C, we just multiply it by
\( {\bf A}^{-1} \) and subtract the corresponding block.
Now we illustrate Gauss elimination algorithm when \( (m+n) \times (m+n) \) matrix M is
partitioned into blocks \( {\bf M} = \begin{bmatrix} {\bf A} & {\bf B} \\ {\bf C} & {\bf D} \end{bmatrix} ,\)
where A is \( n \times n \) nonsingular matrix, B is \( n \times m \) matrix,
C is \( m \times n \) matrix, and D is \( m \times m \) square matrix. Multiplying M
by a "triangular" block matrix, we obtain
\[
\left[ \begin{array}{c|c} {\bf I}_{n \times n} & {\bf 0}_{n\times m} \\ \hline -{\bf C}_{m\times n} {\bf A}^{-1}_{n\times n} & {\bf I}_{m\times m} \end{array} \right]
\left[ \begin{array}{c|c} {\bf A}_{n\times n} & {\bf B}_{n\times m} \\ \hline {\bf C}_{m\times n} & {\bf D}_{m\times m} \end{array} \right] =
\left[ \begin{array}{c|c} {\bf A}_{n\times n} & {\bf B}_{n\times m} \\ \hline {\bf 0}_{m\times n} & {\bf D}_{m\times m} - {\bf C}\,{\bf A}^{-1} {\bf B} \end{array} \right] .
\]
The
\( m \times m \) matrix in right bottom corner,
\( {\bf D}_{m\times m} - {\bf C}\,{\bf A}^{-1} {\bf B} ,\) is called
Schur complement.
Recall the difference between row echelon form (also called Gauss form) and reduced row echelon form (Gauss--Jordan). The following matrices are in row echelon form but not reduced row echelon form:
\[
\left[ \begin{array}{cccc} 1 & * & * & * \\ 0 & 1 & * & * \\ 0&0&1&* \\ 0&0&0&1
\end{array} \right] , \qquad \left[ \begin{array}{cccc} 1 & * & * & * \\ 0 & 1 & * & * \\ 0&0&1&* \\ 0&0&0&0
\end{array} \right] , \qquad \left[ \begin{array}{cccc} 1 & * & * & * \\ 0 & 1 & * & * \\ 0&0&0&0 \\ 0&0&0&0
\end{array} \right] , \qquad \left[ \begin{array}{cccc} 1 & * & * & * \\ 0 & 0 & 1 & * \\ 0&0&0&1 \\ 0&0&0&0
\end{array} \right] .
\]
All matrices of the following types are in reduced row echelon form:
\[
\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0&0&1&0 \\ 0&0&0&1
\end{array} \right] , \qquad \left[ \begin{array}{cccc} 1 & 0 & 0 & * \\ 0 & 1 & 0 & * \\ 0&0&1&* \\ 0&0&0&0
\end{array} \right] , \qquad \left[ \begin{array}{cccc} 1 & 0 & * & * \\ 0 & 1 & * & * \\ 0&0&0&0 \\ 0&0&0&0
\end{array} \right] , \qquad \left[ \begin{array}{cccc} 0 & 1 & * & 0 \\ 0 & 0 & 0 & 1 \\ 0&0&0&0 \\ 0&0&0&0
\end{array} \right] .
\]
This is an example of using row reduction procedure:
sage: A=matrix(QQ,3,3,[2,-4,1,4,-8,7,-2,4,-3])
sage: b=matrix(QQ,3,1,[4,2,5])
sage: B=A.augment(b) # construct augmented matrix
sage: B.add_multiple_of_row(0,0,-1/2)
[ 1 -2 1/2 2]
[ 4 -8 7 2]
[-2 4 -3 5]
sage: B.add_multiple_of_row(1,0,-4)
[ 1 -2 1/2 2]
[ 0 0 5 -6]
[-2 4 -3 5]
sage: B.add_multiple_of_row(2,0,2)
[ 1 -2 1/2 2]
[ 0 0 5 -6]
[ 0 0 -2 9]
sage: B.add_multiple_of_row(1,1,-4/5)
[ 1 -2 1/2 2 ]
[ 0 0 1 -6/5]
[ 0 0 -2 9 ]
sage: B.add_multiple_of_row(2,1,2)
[ 1 -2 1/2 2]
[ 0 0 1 -6/5]
[ 0 0 0 33/5]
Therefore, we obtained Gauss form for the augmented matrix. Now we need to repeat similar procedure to obtain Gauss-Jordan form. This can be achieved with a standard Sage command:
sage: B.echelon_form()
[ 1 -2 0 0]
[ 0 0 1 0]
[ 0 0 0 1]
We demonstrate Gauss-Jordan procedure in the following example.
Example. Solve the linear vector equation \( {\bf A}\,{\bf x} = {\bf b} , \) where
\[
{\bf A} = \left[ \begin{array}{ccc} -4 &1&1 \\ -1 &4&2 \\ 2&2&-3 \end{array} \right] , \qquad {\bf b} = \left[ \begin{array}{c}
6 \\ -1 \\ 20 \end{array} \right] .
\]
sage: A=matrix(QQ,3,3,[[-4,1,1],[-1,4,2],[2,2,-3]]);A
[ -4 1 1]
[ -1 4 2]
[ 2 2 -3]
sage: A.swap_rows(0,1);A
[ -1 4 2]
[ -4 1 1]
[ 2 2 -3]
sage: A.swap_columns(0,1);A
[ 1 -4 2]
[ 4 -1 1]
[ 2 2 -3]
sage: b=vector([6,-1,-20])
sage: B=A.augment(b);B
[ -4 1 1 6]
[ -1 4 2 -1]
[ 2 2 -3 -20]
sage: B.rref()
[ 1 0 0 -61/55]
[ 0 1 0 -144/55]
[ 0 0 1 46/11]
So the last column gives the required vector x.
Another way of expressing to say a system is consistent if and only
if column
n + 1 is not a pivot column of
B
. Sage has the matrix method
.pivot()
to
easily identify the pivot columns of a matrix. Let’s consider as an example.
sage: coeff = matrix(QQ, [[ 2, 1, 7, -7],
... [-3, 4, -5, -6],
... [ 1, 1, 4, -5]])
sage: const = vector(QQ, [2, 3, 2])
sage: aug = coeff.augment(const)
sage: aug.rref()
[1 0 3-2 0]
[0 1 1-3 0]
[0 0 0 0 1]
sage: aug.pivots()
(0, 1, 4)
We can look at the reduced row-echelon form of the augmented matrix and see
a leading one in the final column, so we know the system is inconsistent. However,
we could just as easily not form the reduced row-echelon form and just look at the
list of pivot columns computed by
aug.pivots(). Since aug has 5 columns, the final
column is numbered 4, which is present in the list of pivot columns, as expected.
Example. We demonstrate the Gaussian method with Gauss--Jordan elimination by solving the same system of algebraic equations with two distinct given vectors:
\[
\begin{split}
x_1 + 2\,x_2 + 3\,x_3 &= 4,
\\
2\,x_1 + 5\,x_2 + 3\,x_3 &= 5, \\
x_1 + 8\,x_3 &= 9 ;
\end{split} \qquad\mbox{and} \qquad \begin{split}
x_1 + 2\,x_2 + 3\,x_3 &= 1,
\\
2\,x_1 + 5\,x_2 + 3\,x_3 &= 6, \\
x_1 + 8\,x_3 &= -6 .
\end{split}
\]
The row echelon form of the former system of equations is
\[
\left[ \begin{array}{ccc|c} 1&2&3&4 \\ 0&1&-3&-3 \\ 0&0&-1&-1
\end{array} \right] .
\]
Therefore its solution becomes
\( x_1 = 1, \ x_2 =0, \ x_3 =1 . \) The augmented matrix for the
latter system can be reduced to
\[
\left[ \begin{array}{ccc|c} 1&0&0&2 \\ 0&1&0&1 \\ 0&0&1&-1
\end{array} \right] ,
\]
which leads to the solution
\( x_1 = 2, \ x_2 =1, \ x_3 =-1 . \)
Example. What conditions must \( b_1 , \) \( b_2 , \) and
\( b_3 \) satisfy in order for the system
\[
\begin{split}
x_1 + x_2 + 2\,x_3 &= b_1 ,
\\
x_1 + x_3 &= b_2 , \\
2\,x_1 + x_2 + 3\,x_3 &= b_3
\end{split}
\]
to be consistent?
The augmented matrix corresponding to the symmetric coefficient matrix is
\[
\left[ \begin{array}{ccc|c}
1&1&2& b_1 \\
1&0&1& b_2 \\
2&1&3& b_3 \end{array} \right] ,
\]
which can be reduced to row echelon form as follows
\begin{align*}
\left[ {\bf A} \,| \,{\bf b} \right] &= \left[ \begin{array}{ccc|c} 1&1&2& b_1 \\
0&-1&-1& b_2 -b_1 \\
0&-1&-1& b_3 - 2\,b_1 \end{array} \right] \qquad \begin{array}{l} -1 \mbox{ times the first row was added to the} \\
\mbox{second and $-1$ times the first row was added to the third} \end{array}
\\
&= \left[ \begin{array}{ccc|c} 1&1&2& b_1 \\
0&1&1& b_1 - b_2 \\ 0&-1&-1& b_3 -2\, b_1 \end{array} \right] \qquad \begin{array}{l}
\mbox{the second row was } \\ \mbox{multiplied by $-1$} \end{array}
\\
&= \left[ \begin{array}{ccc|c} 1&1&2& b_1 \\
0&1&1& b_1 - b_2 \\
0&0&0& b_3 - b_2 - b_1 \end{array} \right] \qquad \begin{array}{l} \mbox{the second row was added} \\
\mbox{to the third} \end{array} .
\end{align*}
It is now evident from the third row in the matrix that the system has a solution if and only if
\( b_1 , \) \( b_2 , \) and
\( b_3 \) satisfy the condition
\[
b_3 - b_2 -b_1 =0 \qquad\mbox{or} \qquad b_3 = b_1 + b_2 .
\]
To express this condition another way,
\( {\bf A}\, {\bf x} = {\bf b} \) is consistent if and only if
b is the vector of the form
\[
{\bf b} = \begin{bmatrix} b_1 \\ b_2 \\ b_1 + b_2 \end{bmatrix} = b_1 \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} + b_2
\begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} ,
\]
where
\( b_1 \) and
\( b_2 \) are arbitrary. The vectors
\( \langle 1, 0 , 1 \rangle^T ,\) \( \langle 0 , 1, 1 \rangle^T \)
constudute the basis in the column space of the coefficient matrix. ■
LU-factorization
Recall that in Gaussian
Elimination, row operations are used to change the coefficient matrix to an upper
triangular matrix. The solution is then found by back substitution, starting from the
last equation in the reduced system. In Gauss-Jordan Reduction, row operations are
used to diagonalize the coefficient matrix, and the answers are read directly.
The goal of this section is to identify Gaussian elimination with LU factorization. The original matrix A
becomes the product of two or more special matrices that are actually triangular matrices. Namely, the factorization comes from elimination:
\( {\bf A} = {\bf L}\,{\bf U} , \) where L is lower triangular matrix and U is upper triangular matrix.
Such representation is called and LU-decomposition of LU-factorization. Computers
usually solve square systems of linear equations using the LU decomposition, and it is also a key step when inverting
a matrix, or computing the determinant of a matrix. The LU decomposition was introduced by a
Polish astronomer, mathematician, and geodesist Tadeusz Banachiewicz (1882--1954) in 1938.
For a single linear system \( {\bf A}\,{\bf x} = {\bf b} \) of n equations in n
unknowns, the methods LU-decomposition and Gauss-Jordan elimination differ in bookkeeping but otherwise involve the same number of flops. However,
LU-factorization has the following advantages:
- Gaussian elimination and Gauss--Jordan elimination both use the augmented matrix \( \left[ {\bf A} \, | \, {\bf b} \right] ,\)
so b must be known. In contrast, LU-decomposition uses only matrix A, so once that factorization is complete, it can be applied to any vector b.
- For large linear systems in which computer memory is at a premium, one can dispense with the storage of the 1's
and zeroes that appear on or below the main diagonal of U, since those entries are known. The space
that this opens up can then be used to store the entries of L.
Not every square matrix has an LU-factorization. However, if it is possible to reduce a square matrix A to row
echelon form by Gaussian elimination without performing any row interchanges, then A will have an LU-decomposition, though
it may not be unique.
LU-decomposition:
Step 1: rewrite the system of algebraic equations \( {\bf A} {\bf x} = {\bf b} \) as
\[
{\bf L}{\bf U} {\bf x} = {\bf b} .
\]
Step 2: Define a new
\( n\times 1 \) matrix
y (which is actually a vector)
by
\[
{\bf U} {\bf x} = {\bf y} .
\]
Step 3:
Rewrite the given equation as
\( {\bf L} {\bf y} = {\bf b} \) and solve this sytem for
y.
Step 4: Substitute y into the equation
\( {\bf U} {\bf x} = {\bf y} \) and solve for
x.
Procedure for constructing LU-decomposition:
Step 1: Reduce \( n \times n \) matrix A
to a row echelon form U by Gaussian elimination without row interchanges, keeping track of the multipliers
used to introduce the leading coefficients (usually 1's) and multipliers used to introduce the zeroes below
the leading coefficients.
Step 2: In each position along the main diagonal L, place the reciprocal of the multiplier
that introduced the leading 1 in that position of U.
Step 3:
In each position below the main diagonal of L, place the negative of the multiplier used to introduce the zero
in that position of U.
Step 4: For the decomposition \( {\bf A} = {\bf L} {\bf U} . \)
Recall the elementary operations on the rows of a matrix that are
equivalent to premultiplying by an elementary matrix E:
(1) multiplying row i by a nonzero scalar α , denoted by \( {\bf E}_i (\alpha ) ;\)
(2) adding β times row j to row i, denoted by \( {\bf E}_{ij} (\beta ) \) (here β is any
scalar), and
(3) interchanging rows i and j, denoted by \( {\bf E}_{ij} \) (here \( i \ne j \) ),
called elementary row operations of types 1,2 and 3, respectively.
Correspondingly, a square matrix E is called an elementary matrix if it can be obtained
from an identity matrix by performing a single elementary operation.
Theorem: Every elementary matrix is invertible, and the inverse is also an elementary matrix. ■
Example.
Illustrations for m = 4:
\[
{\bf E}_3 (\alpha ) = \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&\alpha &0 \\ 0&0&0&1 \end{bmatrix} , \qquad
{\bf E}_{42} (\beta ) = \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1 &0 \\ 0&\beta&0&1 \end{bmatrix} , \qquad
{\bf E}_{13} = \begin{bmatrix} 0 &0&1&0 \\ 0&1&0&0 \\ 1&0&0 &0 \\ 0&0&0&1 \end{bmatrix} .
\]
Correspondingly, we have their inverses:
\[
{\bf E}_3^{-1} (\alpha ) = \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&\alpha^{-1} &0 \\ 0&0&0&1 \end{bmatrix} , \qquad
{\bf E}_{42}^{-1} (\beta ) = \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1 &0 \\ 0&-\beta&0&1 \end{bmatrix} , \qquad
{\bf E}_{13}^{-1} = \begin{bmatrix} 0 &0&1&0 \\ 0&1&0&0 \\ 1&0&0 &0 \\ 0&0&0&1 \end{bmatrix} .
\]
Multiplying by an arbitrary matrix
\[
{\bf A} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} ,
\]
we obtain
\begin{align*}
{\bf E}_3 (\alpha )\,{\bf A} &= \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\
\alpha \,a_{31} & \alpha \,a_{32} & \alpha \,a_{33} & \alpha \,a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} , \quad
{\bf A} \, {\bf E}_3 (\alpha ) = \begin{bmatrix} a_{11} & a_{12} & \alpha \,a_{13} & a_{14} \\ a_{21} & a_{22} & \alpha \,a_{23} & a_{24} \\
a_{31} & a_{32} & \alpha \,a_{33} & a_{34} \\ a_{41} & a_{42} & \alpha \,a_{43} & a_{44} \end{bmatrix} ,
\\
{\bf E}_{42} (\beta ) \, {\bf A} &= \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\
\alpha \,a_{31} & \alpha \,a_{32} & \alpha \,a_{33} & \alpha \,a_{34} \\ a_{41} + \beta \,a_{21} & a_{42} + \beta \,a_{22} & a_{43} + \beta \,a_{23}& a_{44} + \beta \,a_{24} \end{bmatrix} , \quad
\\
{\bf A} \, {\bf E}_{42} (\beta ) &= \begin{bmatrix} a_{11} & a_{12} + \beta\, a_{14} & a_{13} & a_{14} \\ a_{21} & a_{22} + \beta \,a_{24}& a_{23} & a_{24} \\
a_{31} & a_{32} + \beta\, a_{34}& a_{33} & a_{34} \\ a_{41} & a_{42} + \beta \,a_{44}& a_{43} & a_{44} \end{bmatrix} ,
\\
{\bf E}_{13} \,{\bf A} &= \begin{bmatrix} a_{31} & a_{32} & a_{33} & a_{34} \\ a_{21} & a_{22} & a_{23} & a_{24} \\
a_{11} & a_{12} & a_{13} & a_{14} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} = {\bf A}\, {\bf E}_{13} .
\end{align*}
Example.
We find LU-factorization of
\[
{\bf A} = \begin{bmatrix} 2&6&2 \\ -3&-8&0 \\ 4&9&2 \end{bmatrix} .
\]
To achieve this, we reduce A to a row echelon form U using Gaussian elimination and then calculate L by inverting the product of elementary matrices.
| Reduction |
Row operation |
Elementary matrix |
Inverse matrix |
| \( \begin{bmatrix} 2&6&2 \\ -3&-8&0 \\ 4&9&2 \end{bmatrix} \) |
|
|
|
| Step 1: |
\( \frac{1}{2} \times \,\mbox{row 1} \) |
\( {\bf E}_1 = \begin{bmatrix} 1/2&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \) |
\( {\bf E}_1^{-1} = \begin{bmatrix} 2&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \) |
| \( \begin{bmatrix} 1&3&1 \\ -3&-8&0 \\ 4&9&2 \end{bmatrix} \) |
|
|
|
| Step 2 |
\( 3 \times \,\mbox{row 1} + \mbox{row 2}\) |
\( {\bf E}_2 = \begin{bmatrix} 1&0&0 \\ 3&1&0 \\ 0&0&1 \end{bmatrix} \) |
\( {\bf E}_2^{-1} = \begin{bmatrix} 1&0&0 \\ -3&1&0 \\ 0&0&1 \end{bmatrix} \) |
| \( \begin{bmatrix} 1&3&1 \\ 0&1&3 \\ 4&9&2 \end{bmatrix} \) |
|
|
|
| Step 3 |
\( -4 \times \,\mbox{row 1} + \mbox{row 3}\) |
\( {\bf E}_3 = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ -4&0&1 \end{bmatrix} \) |
\( {\bf E}_3^{-1} = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 4&0&1 \end{bmatrix} \) |
| \( \begin{bmatrix} 1&3&1 \\ 0&1&3 \\ 0&-3&-2 \end{bmatrix} \) |
|
|
|
| Step 4 |
\( 3 \times \,\mbox{row 2} + \mbox{row 3}\) |
\( {\bf E}_4 = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&3&1 \end{bmatrix} \) |
\( {\bf E}_4^{-1} = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&-3&1 \end{bmatrix} \) |
| \( \begin{bmatrix} 1&3&1 \\ 0&1&3 \\ 0&0&7 \end{bmatrix} \) |
|
|
|
| Step 5 |
\( \frac{1}{7} \times \,\mbox{row 3} \) |
\( {\bf E}_5 = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1/7 \end{bmatrix} \) |
\( {\bf E}_5^{-1} = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&7 \end{bmatrix} \) |
| \( \begin{bmatrix} 1&3&1 \\ 0&1&3 \\ 0&0&1 \end{bmatrix} = {\bf U}\) |
|
|
|
Now we find the lower triangular matrix:
\begin{align*}
{\bf L} &= {\bf E}_1^{-1} {\bf E}_2^{-1} {\bf E}_3^{-1} {\bf E}_4^{-1} {\bf E}_5^{-1}
\\
&= \begin{bmatrix} 2&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} 1&0&0 \\ -3&1&0 \\ 0&0&1 \end{bmatrix}
\begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 4&0&1 \end{bmatrix} \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&-3&1 \end{bmatrix} \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&7 \end{bmatrix}
\\
&= \begin{bmatrix} 2&0&0 \\ -3&1&0 \\ 4&-3&7 \end{bmatrix} ,
\end{align*}
so
\[
{\bf A} = \begin{bmatrix} 2&6&2 \\ -3&-8&0 \\ 4&9&2 \end{bmatrix} = \begin{bmatrix} 2&0&0 \\ -3&1&0 \\ 4&-3&7 \end{bmatrix}\, \begin{bmatrix} 1&3&1 \\ 0&1&3 \\ 0&0&1 \end{bmatrix} = {\bf L}\,{\bf U} .
\]
Example. Consider the \( 3\times 4 \) matrix
\[
{\bf A} = \begin{bmatrix} 1&0&2&3 \\ 2&-1&3&6 \\ 1&4&4&0 \end{bmatrix}
\]
and consider the elementary matrix
\[
{\bf E}_{31} (-1) = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ -1&0&1 \end{bmatrix} ,
\]
which results from adding
\( -1 \) times the first row of
\( {\bf I}_3 \) to the thrid row. The product
\( {\bf E}_{31} (-1)\, {\bf A} \) is
\[
{\bf E}_{31} (-1)\,\, {\bf A} = \begin{bmatrix} 1&0&2&3 \\ 2&-1&3&6 \\ 0&4&2&-3 \end{bmatrix} ,
\]
which is precisely the matrix that results when we add
\( -1 \) times the first row of
A to the third row. ■
PLU Factorization
So far, we tried to represent a square nonsingular matrix
A as a product of a lower-triangular matrix
L and an upper triangular matrix
U:
\( {\bf A} = {\bf L}\,{\bf U} .\)
When this is possible we say that
A has an LU-decomposition (or factorization). It turns out that
this factorization (when it exists) is not unique. If
L has 1's on it's diagonal, then it is called
a Doolittle factorization. If
U has 1's on its diagonal, then it is called a Crout factorization.
When
L is an unitary matrix, it is called a Cholesky decomposition. Moreover, Gaussian elimination in its pure form may be unstable.
While LU-decomposition is a useful computational tool, but this does not work for
every matrix. Consider even the simple example with matrix
\[
{\bf A} = \begin{bmatrix} 0&2 \\ 3 & 0 \end{bmatrix} .
\]
Another cause of instability in Gaussian elimination is when encountering relatively small pivots.
Gaussian elimination is guaranteed to succeed if row or column interchanges are used in order to
avoid zero pivots when using exact calculations. But, when computing the LU factorization
numerically, this is not necessarily true. When a calculation is undefined because of division by zero, the
same calculation will suffer numerical difficulties when there is division by a nonzero number that
is relatively small.
\[
{\bf A} = \begin{bmatrix} 10^{-22}&2 \\ 1 & 3 \end{bmatrix} .
\]
When computing the factors
L and
U, the process does not fail in this case because there is no
division by zero.
\[
{\bf L} = \begin{bmatrix} 1&0 \\ 10^{22} & 1 \end{bmatrix} , \qquad {\bf U} = \begin{bmatrix} 10^{-22}&2 \\ 0 & 3 - 2\cdot 10^{22} \end{bmatrix} .
\]
When these computations are performed in floating point arithmetic, the number
\( 3 - 2\cdot 10^{22} \)
is not represented exactly but will be rounded to the nearest floating point number which we will say
is
\( 2\cdot 10^{22} . \) This means that our matrices are now floating point matrices
L' and
U':
\[
{\bf L}' = \begin{bmatrix} 1&0 \\ 10^{22} & 1 \end{bmatrix} , \qquad {\bf U}' = \begin{bmatrix} 10^{-22}&2 \\ 0 & - 2\cdot 10^{22} \end{bmatrix} .
\]
When we compute
L'U', we get
\[
{\bf L}' {\bf U}' = \begin{bmatrix} 10^{-22}&2 \\ 1 & 0 \end{bmatrix} .
\]
The answer should be equal to
A, but obviously that is not the case. The 3 in position
(2,2) of matrix
A is now 0. Also, when trying to solve a system such as
\( {\bf A} \, {\bf x} = {\bf b} \)
using the LU factorization, the factors
L'U' would not give you a correct answer. The
LU factorization was a stable computation but not backward stable.
Recall that an \( n \times n \) permutation matrix P is a matrix with
precisely one entry whose value is "1" in each column and row, and all of whose other entries are "0." The rows of
P are a permutation of the rows of the identity matrix. Since not every matrix has LU decomposition,
we try to find a permulation matrix P such that PA has LU factorization:
\( {\bf P}\,{\bf A} = {\bf L}\,{\bf U} , \) where L and U
are again lower and upper triangular matrices, and P is a permutation matrix. In this case, we say that A has a PLU factorization.
It is also referred to as the LU factorization with Partial Pivoting (LUP) with row permutations only. An
LU factorization with full pivoting involves both row and column permutations, \( {\bf P}\,{\bf A}\, {\bf Q} = {\bf L}\,{\bf U} , \)
where L and U, and P are defined as before, and Q is a permutation matrix that reorders the columns of A.
For a permutation matrix P, the product PA is a new matrix whose rows consists
of the rows of A rearranged in the new order. Note that a product of permutation matrices is a permutation matrix.
Every permutation matrix is an orthogonal matrix: \( {\bf P}^{-1} = {\bf P}^{\mathrm T} . \)
Example. Let P be a permutation matrix that interchange rows 1 and 2 and
also interchange rows 3 and 4:
\[
{\bf P}\, {\bf A} = \begin{bmatrix} 0&1&0&0 \\ 1&0&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \end{bmatrix}
\begin{bmatrix} a_{1,1}&a_{1,2}&a_{1,3}&a_{1,4} \\ a_{2,1}&a_{2,2}&a_{2,3}&a_{2,4} \\ a_{3,1}&a_{3,2}&a_{3,3}&a_{3,4} \\ a_{4,1}&a_{4,2}&a_{4,3}&a_{4,4} \end{bmatrix} =
\begin{bmatrix} a_{2,1}&a_{2,2}&a_{2,3}&a_{2,4} \\ a_{1,1}&a_{1,2}&a_{1,3}&a_{1,4} \\ a_{4,1}&a_{4,2}&a_{4,3}&a_{4,4} \\ a_{3,1}&a_{3,2}&a_{3,3}&a_{3,4} \end{bmatrix} .
\]
However,
\[
{\bf A} {\bf P} = \begin{bmatrix} a_{1,1}&a_{1,2}&a_{1,3}&a_{1,4} \\ a_{2,1}&a_{2,2}&a_{2,3}&a_{2,4} \\ a_{3,1}&a_{3,2}&a_{3,3}&a_{3,4} \\ a_{4,1}&a_{4,2}&a_{4,3}&a_{4,4} \end{bmatrix}
\begin{bmatrix} 0&1&0&0 \\ 1&0&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \end{bmatrix} =
\begin{bmatrix} a_{1,2}&a_{1,1}&a_{1,4}&a_{1,3} \\ a_{2,2}&a_{2,1}&a_{2,4}&a_{2,3} \\ a_{3,2}&a_{3,1}&a_{3,4}&a_{3,3} \\ a_{4,2}&a_{4,1}&a_{4,4}&a_{4,3} \end{bmatrix} .
\]
Theorem: If A is a nonsingular matrix, then there exists a
permutation matrix P so that PA has an LU-factorization.
■
Pivoting for LU factorization is the process of systematically selecting pivots for Gaussian elimination during
the LU-decomposition of a matrix. The LU factorization is closely related to Gaussian
elimination, which is unstable in its pure form. To guarantee the elimination process goes to completion, we must
ensure that there is a nonzero pivot at every step of the elimination process. This is the reason we need pivoting
when computing LU decompositions. But we can do more with pivoting than just making sure Gaussian elimination
completes. We can reduce roundoff errors during computation and make our algorithm backward stable by implementing
the right pivoting strategy. Depending on the matrix A, some LU
decompositions can become numerically unstable if relatively
small pivots are used. Relatively small pivots cause instability because they operate very similar
to zeroes during Gaussian elimination. Through the process of pivoting, we can greatly reduce this
instability by ensuring that we use relatively large entries as our pivot elements. This prevents large
factors from appearing in the computed L and U, which reduces roundoff errors during computation.
The goal of partial pivoting is to use a permutation matrix to place the largest entry of the first
column of the matrix at the top of that first column. For an \( n \times n \)
matrix A, we scan n rows of the first column for the largest value. At step k
of the elimination, the pivot we choose is the largest of the n- (k+1)
subdiagonal entries of column k, which costs O(nk) operations for each step of the
elimination. So for an n-by-n matrix, there is a total of \( O(n^2 ) \)
comparisons. Once located, this entry is then moved into the pivot position
\( A_{k,k} \) on the diagonal of the matrix.
Example. Use PLU factorization to solve the linear system
\[
\begin{bmatrix} 2&4&2 \\ 4&-10&2 \\ 1&2&4 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} =
\begin{bmatrix} 5 \\ -8 \\ 13 \end{bmatrix} .
\]
We want to use a permutation matrix to place the largest entry of the first column
into the position
(1,1). For this matrix, this means we want 4 to be the first entry of the first column.
So we use the permutation matrix
\[
{\bf P}_1 = \begin{bmatrix} 0&1&0 \\ 1&0&0 \\ 0&0&1 \end{bmatrix} \qquad \Longrightarrow \qquad {\bf P}_1 {\bf A} =
\begin{bmatrix} 4&-10&2 \\ 2&4&2 \\ 1&2&4 \end{bmatrix} .
\]
Then we use the matrix
M to eliminate the bottom two entries of the first column:
\[
{\bf M}_1 = \begin{bmatrix} 1&0&0 \\ -2/4&1&0 \\ -1/4&0&1 \end{bmatrix} \qquad \Longrightarrow \qquad {\bf M}_1 {\bf P}_1 {\bf A} =
\begin{bmatrix} 4&-10&2 \\ 0&9&1 \\ 0&9/2&7/2 \end{bmatrix} .
\]
For latter matrix we don't need pivoting because the middle of the second row is the largest. So we just multiply by
\[
{\bf M}_2 = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&-1/2&1 \end{bmatrix} \qquad \Longrightarrow \qquad {\bf M}_2 {\bf M}_1 {\bf P}_1 {\bf A} =
\begin{bmatrix} 4&-10&2 \\ 0&9&1 \\ 0&0&3 \end{bmatrix} .
\]
Since the inverse of
\( {\bf M}_2 {\bf M}_1 \) is the required lower triangular matrix
\[
{\bf M}_2 {\bf M}_1 = \begin{bmatrix} 1&0&0 \\ -1/2&1&0 \\ 0&-1/2&1 \end{bmatrix} \qquad \Longrightarrow \qquad
{\bf L} = \left( {\bf M}_2 {\bf M}_1 \right)^{-1} =
\begin{bmatrix} 1&0&0 \\ 1/2&1&0 \\ 1/4&1/2&1 \end{bmatrix} ,
\]
we have
\[
{\bf A} = \begin{bmatrix} 2&4&2 \\ 4&-10&2 \\ 1&2&4 \end{bmatrix} , \quad {\bf L} = \begin{bmatrix} 1&0&0 \\ 1/2&1&0 \\ 1/4&1/2&1 \end{bmatrix} , \quad
{\bf U} = \begin{bmatrix} 4&-10&2 \\ 0&9&0 \\ 0&0&7/2 \end{bmatrix} , \quad {\bf P} = \begin{bmatrix} 0&1&0 \\ 1&0&0 \\ 0&0&1 \end{bmatrix} ,
\]
then
\[
{\bf L}{\bf U} = \begin{bmatrix} 4&-10&2 \\ 2&4&1 \\ 1&2&4 \end{bmatrix} , \quad {\bf P}{\bf A} = \begin{bmatrix} 4&-10&2 \\ 2&4&1 \\ 1&2&4 \end{bmatrix} .
\]
Thus, the solution becomes
\[
{\bf x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \\ 3 \end{bmatrix} .
\]
Algorithm for PLU-factorization: is based on the following formula for upper triangular matrix
\( {\bf U} = \left[ u_{i,j} \right] : \)
\[
u_{i,j} = a_{i,j} - \sum_{k=1}^{i-1} u_{k,j} l_{i.k} ,
\]
with similar formula for
\( {\bf L} = \left[ l_{i,j} \right] . \) To ensure that the algorithm is numerically stable when
\( u_{j,j} \ll 0, \)
a pivoting matrix
P is used to re-order
A so that the largest element of each
column of
A gets shifted to the diagonal of
A. The formula for elements of
L follows:
\[
l_{i,j} = \frac{1}{u_{j,j}} \left( a_{i,j} - \sum_{k=1}^{j-1} u_{k,j} l_{i,k} \right) .
\]
Step 1: If \( n=1 , \) return \( {\bf P} =1, \quad {\bf L} = 1, \quad {\bf U} = a_{1,2} . \)
Step 2: Find a non-zero element \( a_{i,1} \) in the first row of A.
(If not, then the system is not solvable.)
Step 3: Define a permutation matrix \( {\bf Q}_{n \times n} \)
such that
-
\( q_{i,1} = q_{1,i} =1 . \)
-
\( q_{j,j} =1 \) for \( j \ne 1, \ j\ne i . \)
- All the other elements of Q are 0. ■
Step 4: Let \( {\bf B} = {\bf Q} {\bf A} . \)
Note that \( b_{1,1} = a_{i,1} \ne 0. \)
Step 5: Write B as \( {\bf B} =
\begin{bmatrix} b_{1,1} & {\bf r}^{\mathrm T} \\ {\bf c} & {\bf C}_1 \end{bmatrix} . \)
Step 6: Define \( {\bf B}_1 = {\bf C}_1 - {\bf c} \cdot {\bf r}^{\mathrm T} / b_{1,1} .\)
Recursively compute \( {\bf B}_1 = {\bf P}_1 {\bf L}_1 {\bf U}_1 . \)
Step 7:
\[
{\bf P} = {\bf Q}^{\mathrm T} \begin{bmatrix} 1&0 \\ 0& {\bf P}_1 \end{bmatrix} , \qquad
{\bf L} = \begin{bmatrix} 1&0 \\ {\bf P}_1^{\mathrm T} {\bf c}/ b_{1,1} & {\bf L}_1 \\ \end{bmatrix} , \qquad
{\bf U} = \begin{bmatrix} b_{1,1}&{\bf r}^{\mathrm T} \\ 0& {\bf U}_1 \end{bmatrix} . \quad ■
\]
When employing the
complete pivoting strategy we scan for the largest value in the entire submatrix
\( {\bf A}_{k:n,k:n} , \) where
k is the number of the elimination, instead of
just the next subcolumn. This requires
\( O \left( (n-k)^2 \right) \) comparisons for
every step in the elimination to find the pivot. The total cost becomes
\( O \left( n^3 \right) \) comparisons for an
n-by-
n matrix. For an
\( n \times n \) matrix
A, the first step is to scan
n rows and
n columns for the largest value. Once located, this entry is then permuted into the
next diagonal pivot position of the matrix. So in the first step the entry is permuted into the
(1,1)
position of matrix
A. We interchange rows exactly as we did in partial pivoting, by multiplying
A on the left with a permutation matrix
P. Then to interchange columns, we multiply
A on the right by another permutation matrix
Q. The matrix product
PAQ interchanges rows and columns accordingly so that the largest entry in the matrix is in the
(1,1) position of
A. With complete pivoting, the general equation for
L
is the same as for partial pivoting, but the equation for
U is slightly different.
Complete pivoting is theoretically the most stable strategy
as it can be used even when a matrix is singular, but it is much slower than partial pivoting.
Example.
Consider the matrix A:
\[
{\bf A} = \begin{bmatrix} 2&3&4 \\ 4&7&5 \\ 4&9&5 \end{bmatrix} .
\]
In this case, we want to use two different permutation matrices to place the largest entry of the entire matrix
into the position
\( A_{1,1} .\) For the given matrix, this means we want 9 to be the
first entry of the first column. To achieve this we multiply A on the left by the permutation matrix
\( {\bf P}_1 \) and multiply on the right by the permutation matrix
\( {\bf Q}_1 .\)
\[
{\bf P}_1 = \begin{bmatrix} 0&0&1 \\ 0&1&0 \\ 1&0&0 \end{bmatrix} , \quad {\bf Q}_1 = \begin{bmatrix} 0&1&0 \\ 1&0&0 \\ 0&0&1 \end{bmatrix} , \quad
{\bf P}_1 {\bf A} {\bf Q}_1 = \begin{bmatrix} 9&4&5 \\ 7&4&5 \\ 3&2&4 \end{bmatrix} .
\]
Then in computing the LU factorization, the matrix
M is used to eliminate the bottom two
entries of the first column:
\[
{\bf M}_1 = \begin{bmatrix} 1&0&0 \\ -7/9&1&0 \\ -1/3&0&1 \end{bmatrix} \qquad \Longrightarrow \qquad {\bf M}_1 {\bf P}_1 {\bf A} {\bf Q}_1 =
\begin{bmatrix} 9&4&5 \\ 0&8/9&10/9 \\ 0&2/3&7/3 \end{bmatrix} .
\]
Then, the permutation matrices
P and
Q are used to move the largest entry of the submatrix
\( {\bf A}_{2:3;2:3} \)
into the position
\( A_{2,2} : \)
\[
{\bf P}_2 = \begin{bmatrix} 1&0&0 \\ 0&0&1 \\ 0&1&0 \end{bmatrix} = {\bf Q}_2 \qquad \Longrightarrow \qquad {\bf P}_2 {\bf M}_1 {\bf P}_1 {\bf A} {\bf Q}_1 {\bf Q}_2 =
\begin{bmatrix} 9&4&5 \\ 0&7/3&2/3 \\ 0&10/9&8/9 \end{bmatrix} .
\]
As we did before, we are going to use matrix multiplication to eliminate entries at the bottom
of the column 2:
\[
{\bf M}_2 = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&-10/21&1 \end{bmatrix} \qquad \Longrightarrow \qquad {\bf M}_2 {\bf P}_2 {\bf M}_1 {\bf P}_1 {\bf A} {\bf Q}_1 {\bf Q}_2 =
\begin{bmatrix} 9&4&5 \\ 0&7/3&2/3 \\ 0&0&4/7 \end{bmatrix} .
\]
This upper triangular matrix product is the
U matrix. The
L matrix comes from the inverse of
the product of
M and
P matrices:
\[
{\bf L} = \left( {\bf M}_2 {\bf P}_2 {\bf M}_1 {\bf P}_1 \right)^{-1} =
\begin{bmatrix} 1&0&0 \\ 1/3&1&0 \\ 7/9&10/21&1 \end{bmatrix} .
\]
To check, we can show that
\( {\bf P} {\bf A} {\bf Q} = {\bf L} {\bf U} , \) where
\( {\bf P} = {\bf P}_2 {\bf P}_1 \) and
\( {\bf Q} = {\bf Q}_1 {\bf Q}_2 . \) ■
Rook pivoting is a third alternative pivoting strategy. For this strategy, in the
kth step of the elimination, where \( 1 \le k \le n-1 \) for an
n-by-n matrix A, we scan the submarix \( {\bf A}_{k:n;k:n} \)
for values that are the largest in their respective row and column. Once we have found our potential pivots,
we are free to choose any that we please. This is because the identified potential pivots are large
enough so that there will be a very minimal difference in the end factors, no matter which pivot is
chosen. When a computer uses rook pivoting, it searches only for the first entry that is the largest
in its respective row and column. The computer chooses the first one it finds because even if there
are more, they all will be equally effective as pivots. This allows for some options in our decision
making with regards to the pivot we want to use.
Example.
Consider the matrix A:
\[
{\bf A} = \begin{bmatrix} 1&4&7 \\ 7&8&2 \\ 9&5&1 \end{bmatrix} .
\]
When using the partial pivoting technique, we would identify 8 as our first pivot element. When
using complete pivoting, we would use 9 as our first pivot element. When rook pivoting we identify
entries that are the largest in their respective rows and columns. So following this logic, we identify
8, 9, and 7 all as potential pivots. In this example we will choose 7 as the first pivot. Since we are
choosing 7 for our first pivot element, we multiply
A on the right by the permutation matrix
Q to move 7 into the position (1,1). Note that we will also multiply on the left of
A
by
P, but
P is simply the identity matrix so there will be no effect on
A.
\[
{\bf Q}_1 = \begin{bmatrix} 0&0&1 \\ 0&1&0 \\ 1&0&0 \end{bmatrix} \qquad\Longrightarrow \qquad {\bf P}_1 {\bf A} {\bf Q}_1 =
\begin{bmatrix} 7&4&1 \\ 2&8&7 \\ 1&5&9 \end{bmatrix} .
\]
Then we eliminate the entries in row 2 and 3 of column 1 via the matrix
\[
{\bf M}_1 = \begin{bmatrix} 1&0&0 \\ -2/7&1&0 \\ -1/7&0&1 \end{bmatrix} \qquad\Longrightarrow \qquad {\bf M}_1 {\bf P}_1 {\bf A} {\bf Q}_1 =
\begin{bmatrix} 7&4&1 \\ 0&48/7&47/7 \\ 0&30/7&62/7 \end{bmatrix} .
\]
If we were employing partial pivoting, our pivot would be 48/7 and if we were using complete
pivoting, our pivot would be 62/7. But using the rook pivoting strategy allows us to choose either
48/7 or 62/7 as our next pivot. In this situation, we do not need to permute the matrix
\( {\bf M}_1 {\bf P}_1 {\bf A}\,{\bf Q}_1 \) to
continue with our factorization because one of our potential pivots is already in pivot postion. To
keep things interesting, we will permute the matrix anyway and choose 62/7
to be our next pivot. To achieve this we wil multiply by the matrix
\( {\bf P}_2 \)
on the left and by the matrix
\( {\bf Q}_2 \) on the right.
\[
{\bf P}_2 = \begin{bmatrix} 1&0&0 \\ 0&0&1 \\ 0&1&0 \end{bmatrix} = {\bf Q}_2 \qquad\Longrightarrow \qquad {\bf P}_2 {\bf M}_1 {\bf P}_1 {\bf A} {\bf Q}_1 {\bf Q}_2 =
\begin{bmatrix} 7&1&4 \\ 0&62/7&30/7 \\ 0&47/7&48/7 \end{bmatrix} .
\]
At this point, we want to eliminate the last entry of the second column to complete the factorization. We achieve
this by matrix
\( {\bf M}_2 :\)
\[
{\bf M}_2 = \begin{bmatrix} 1&0&0 \\ 0&0&1 \\ 0&-47/62&1 \end{bmatrix} \qquad\Longrightarrow \qquad {\bf M}_2 {\bf P}_2 {\bf M}_1 {\bf P}_1 {\bf A} {\bf Q}_1 {\bf Q}_2 =
\begin{bmatrix} 7&1&4 \\ 0&62/7&30/7 \\ 0&0&7/2 \end{bmatrix} .
\]
After the elimination the matrix is now upper triangular which we recognize as the factor
U. The factor
L is equal to the matrix product
\( {\bf L} = \left( {\bf M}_2 {\bf P}_2 {\bf M}_1 {\bf P}_1 \right)^{-1} . \) You can use Sage to check that
PAQ = LU, where
\( {\bf P} = {\bf P}_2 {\bf P}_1 \) and
\( {\bf Q} = {\bf Q}_1 {\bf Q}_2 \)
\begin{align*}
{\bf P\,A\,Q} &= \begin{bmatrix} 1&0&0 \\ 0&0&1 \\ 0&1&0 \end{bmatrix} \begin{bmatrix} 1&4&7 \\ 7&8&2 \\ 9&5&1 \end{bmatrix} \begin{bmatrix} 0&1&0 \\ 0&0&1 \\ 1&0&0 \end{bmatrix} \\
&= \begin{bmatrix} 1&0&0 \\ 1/7&1&0 \\ 2/7&47/62&1 \end{bmatrix} \begin{bmatrix} 7&1&4 \\ 0&62/7&30/7 \\ 0&0&7/2 \end{bmatrix} = {\bf L\,U} .
\end{align*}
sage: nsp.is_finite()
False
Reflection
Suppose that we are given a line spanned over the vector
a in
\( \mathbb{R}^n , \) and we need to find a matrix
H
of reflection about the line through the origin in the plane. This matrix
H should fix every vector on line, and
should send any vector not on the line to its mirror image about the line. The subspace
\( {\bf a}^{\perp} \)
is called the hyperplane in
\( \mathbb{R}^n , \) orthogonal to
a. The
\( n \times n \)
orthogonal matrix
\[
{\bf H}_{\bf a} = {\bf I}_n - \frac{2}{{\bf a}^{\mathrm T} {\bf a}} \, {\bf a} \, {\bf a}^{\mathrm T}
= {\bf I}_n - \frac{2}{\| {\bf a} \|^2} \, {\bf a} \, {\bf a}^{\mathrm T}
\]
is called the Householder matrix or the Householder reflection about
a, named in honor of the American mathematician Alston Householder (1904--1993).
The complexity of the Householder algorithm is \( 2mn^2 - (2/3)\, n^3 \) flops
(arithmetic operations). The Householder matrix \( {\bf H}_{\bf a} \) is symmetric,
orthogonal, diagonalizable, and all its eigenvalues are 1's except one which is -1. Moreover, it is idempotent:
\( {\bf H}_{\bf a}^2 = {\bf I} . \) When \( {\bf H}_{\bf a} \) is applied to a vector x,
it reflects x through hyperplane \( \left\{ {\bf z} \, : \, {\bf a}^{\mathrm T} {\bf z} =0 \right\} . \)
Example.
Consider the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} . \) Then the
Householder reflection with respect to vector u is
\[
{\bf H}_{\bf u} = {\bf I} - \frac{2}{9} \, {\bf u} \,{\bf u}^{\mathrm T} = \frac{1}{9} \begin{bmatrix} 7&4&-4 \\ 4&1&8 \\ -4&8&1 \end{bmatrix} .
\]
The orthogonal symmetric matrix
\( {\bf H}_{\bf u} \) is indeed a reflection because its eigenvalues are -1,1,1,
and it is idempotent. ■
Theorem: If u and v are distinct vectors in
\( \mathbb{R}^n \) with the same norm, then the Householder reflection about the hyperplane
\( \left( {\bf u} - {\bf v} \right)^{\perp} \) maps u into v and conversely.
■
We check this theorem for two-dimensional vectors \( {\bf u} = \left[ u_1 , u_2 \right]^{\mathrm T} \)
and \( {\bf v} = \left[ v_1 , v_2 \right]^{\mathrm T} \) of the same norm. So given
\( \| {\bf v} \| = \| {\bf u} \| , \) we calculate
\[
\| {\bf u} - {\bf v} \|^2 = \| {\bf u} \|^2 + \| {\bf v} \|^2 - \langle {\bf u}, {\bf v} \rangle - \langle {\bf v} , {\bf u} \rangle =
2 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) .
\]
Then we apply the Householder reflection
\( {\bf H}_{{\bf u} - {\bf v}} \) to the vector
u:
\begin{align*}
{\bf H}_{{\bf u} - {\bf v}} {\bf u} &= {\bf u} - \frac{2}{\| {\bf u} - {\bf v} \|^2}
\begin{bmatrix} \left( u_1 - v_1 \right)^2 u_1 + \left( u_1 - v_1 \right) \left( u_2 - v_2 \right) u_2 \\
\left( u_1 - v_1 \right) \left( u_2 - v_2 \right) u_1 + \left( u_2 - v_2 \right)^2 u_2 \end{bmatrix} \\
&= \frac{1}{u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2} \begin{bmatrix} v_1 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) \\
v2 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) \end{bmatrix} = {\bf v} .
\end{align*}
Similarly,
\( {\bf H}_{{\bf u} - {\bf v}} {\bf v} = {\bf u} . \) ■
Example.
We find a Householder reflection that maps the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} \)
into a vector v that has zeroes as its second and third components. Since this vecor has to be of the same norm, we get
\( {\bf v} = \left[ 3, 0 , 0 \right]^{\mathrm T} . \) Since
\( {\bf a} = {\bf u} - {\bf v} = \left[ -2, -2 , 2 \right]^{\mathrm T} , \) the
Householder reflection \( {\bf H}_{{\bf a}} = \frac{1}{3} \begin{bmatrix} 1&-2&2 \\ -2&1&2 \\ 2&2&1 \end{bmatrix} \) maps the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} \)
into a vector v. Matrix \( {\bf H}_{{\bf a}} \) is idempotent (\( {\bf H}_{{\bf a}}^2 = {\bf I} \) ) because its eigenvalues are -1, 1, 1. ■
sage: nsp.is_finite()
False
We use the Householder reflection to obtain an alternative version of LU-decomposition. Consider the following m-by-n matrix:
\[
{\bf A} = \begin{bmatrix} a & {\bf v}^{\mathrm T} \\ {\bf u} & {\bf E} \end{bmatrix} ,
\]
where
u and
v are
m-1 and
n-1 vectors, respectively. Let σ be the
2-norm of the first column of
A. That is, let
\[
\sigma = \sqrt{a^2 + {\bf u}^{\mathrm T} {\bf u}} .
\]
Assume that σ is nonzero. Then the vector
u in the matrix A can be annihilated using a
Householder reflection given by
\[
{\bf P} = {\bf I} - \beta {\bf h}\, {\bf h}^{\mathrm T} ,
\]
where
\[
{\bf h} = \begin{bmatrix} 1 \\ {\bf z} \end{bmatrix} , \quad \beta = 1 + \frac{a}{\sigma_a} , \quad {\bf z} = \frac{\bf u}{\beta \sigma_a} , \quad \sigma_a = \mbox{sign}(a) \sigma .
\]
It is helpful in what follows to define the vectors
q and
p as
\[
{\bf q} = {\bf E}^{\mathrm T} {\bf z} \qquad\mbox{and} \qquad {\bf p} = \beta \left( {\bf v} + {\bf q} \right) .
\]
Then
\[
{\bf P}\,{\bf A} = \begin{bmatrix} \alpha & {\bf w}^{\mathrm T} \\ {\bf 0} & {\bf K} \end{bmatrix} ,
\]
where
\[
\alpha = - \sigma_a , \quad {\bf w}^{\mathrm T} = {\bf v}^{\mathrm T} - {\bf p}^{\mathrm T} , \quad {\bf K} = {\bf E} - {\bf z}\,{\bf p}^{\mathrm T} .
\]
The above formulas suggest the following version of Householder transformations that access the entries of the matrix in a row by row manner.
Algorithm (Row-oriented vertion of Householder transformations):
Step 1: Compute \( \sigma_a \) and β
\[
\sigma = \sqrt{a^2 + {\bf u}^{\mathrm T} {\bf u}} , \qquad \sigma_a = \mbox{sign}(a) \,\sigma , \qquad \beta = a + \frac{a}{\sigma_a} .
\]
Step 2: Compute the factor row \( \left( \alpha , {\bf w}^{\mathrm T} \right) : \)
\[
\alpha = - \sigma_a , \qquad {\bf z} = \frac{\bf u}{\beta \sigma_a} .
\]
Compute the appropriate linear combination of the rows of
A (except for the first column) by computing
\[
{\bf q}^{\mathrm T} = {\bf z}^{\mathrm T} {\bf E}, \qquad {\bf p}^{\mathrm T} = \beta \left( {\bf v}^{\mathrm T} + {\bf q}^{\mathrm T} \right) , \qquad
{\bf w}^{\mathrm T} = {\bf v}^{\mathrm T} - {\bf p}^{\mathrm T} .
\]
Step 3: Apply Gaussian elimination using the pivot row and column from step 2:
\[
\begin{bmatrix} 1 & {\bf p}^{\mathrm T} \\ {\bf z} & {\bf E} \end{bmatrix} \, \rightarrow \,
\begin{bmatrix} 1 & {\bf p}^{\mathrm T} \\ {\bf 0} & {\bf K} \end{bmatrix} ,
\]
where
\( {\bf K} = {\bf E} - {\bf z} \,{\bf p} ^{\mathrm T} . \) ■
This formulation of Householder transformations can be regarded as a special kind of Gauss elimination, where the
pivot row is computed from a linear combination of the rows of the matrix, rather than being taken directly from it.
The numerical stability of the process can be seen from the fact that \( |z_i | \le 1 \) and
\( |w_j | \le \beta \le 2 \) for every entry in z and w.
The Householder algorithm is the most widely used algorithm for QR factorization (for instance, qr in MATLAB) because
it is less sensitive to rounding error than Gram--Schmidt algorithm.
Givens rotation
In numerical linear algebra, a Givens rotation is a rotation in the plane spanned by two coordinates axes.
Givens rotations are named after James Wallace Givens, Jr. (1910--1993), who introduced them to numerical analysis
in the 1950s while he was working at Argonne National Laboratory. A Givens rotation is represented by a matrix of the form
\[
G(i,j,\theta ) = \begin{bmatrix} 1& \cdots & 0 &\cdots & 0 & \cdots & 0 \\
\vdots & \ddots & \vdots && \vdots && \vdots \\
0 & \cdots & c & \cdots & -s & \cdots & 0 \\
\vdots && \vdots & \ddots & \vdots & & \vdots \\
0 & \cdots & s & \cdots & c & \cdots & 0 \\
\vdots && \vdots && \vdots & \ddots & \vdots \\
0 & \cdots & 0 & \cdots & 0 & \cdots & 1
\end{bmatrix} ,
\]
where
\( c= \cos\theta \quad\mbox{and} \quad s= \sin \theta \) appear at the intersections
ith and
jth
rows and columns. The product
\( G(i,j, \theta ){\bf x} \) represents a counterclockwise
rotation of the vector
x in the
(i,j) plane of θ radians, hence the name
Givens rotation.
The main use of Givens rotations in numerical linear algebra is to introduce zeroes in vectors or matrices.
This effect can, for example, be employed for computing the QR decomposition of a matrix. One advantage over
Householder transformations is that they can easily be parallelised, and another is that often for very sparse matrices
they have a lower operation count.
When a Givens rotation matrix, \( G(i,j, \theta ) , \) multiplies another matrix, A,
from the left, \( G(i,j, \theta )\, {\bf A} , \) only rows i and j of A are affected.
Thus we restrict attention to the following counterclockwise problem. Given a and b, find
\( c = \cos\theta \quad \mbox{and} \quad s = \sin\theta \) such that
\[
\begin{bmatrix} c&-s \\ s&c \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} r \\ 0 \end{bmatrix} ,
\]
where
\( r = \sqrt{a^2 + b^2} \) is the length of the vector [
a,
b].
Explicit calculation of θ is rarely necessary or desirable. Instead we directly seek
c and
s.
An obvious solution would be
\[
c \,\leftarrow \,\frac{a}{r} , \qquad s \,\leftarrow \,-\frac{b}{r} .
\]
However, the computation for
r may overflow or underflow. An alternative formulation avoiding this problem is
implemented as the
hypot function in many programming languages.
Row Space and Column Space
If
A is an
\( m\times n \) matrix, then the subspace of
\( \mathbb{R}^n \)
spanned by the row vectors of
A is called the
row space of
A, and the subspace of
\( \mathbb{R}^m \)
spanned by the column vectors of
A is called the
column space of
A or the
range of the matrix. The row space of
A is the column space of the adjoint matrix
\( {\bf A}^{\ast} = \overline{\bf A}^{\mathrm T} = \overline{{\bf A}^{\mathrm T}} ,\)
which is a subspace of
\( \mathbb{R}^n .\)
Theorem: Elementary row operations do not change the row space of a matrix. ■
Theorem: The row space and the column space of a matrix have the same dimension. ■
Theorem: If a matrix R is in row echelon (Gaussian) form, then the row vectors with the leading coefficients (that are usually chosen as 1's)
form a basis for the row space of R, and the column vectors corresponding to the leading coefficients form a basis for the column space. ■
A Basis for the Range: Let \( L:\,\mathbb{R}^n\, \mapsto \, \mathbb{R}^m \)
is a linear transformation given by \( L({\bf x}) = {\bf A}\,{\bf x} , \) for some
\( m \times n \) matrix A. To find a basis for the range of L, perform the
following steps.
Step 1: Find B, the reduced row echelon form of A.
Step 2: Form the set of those columns of A whose corresponding columns in B have nonzero pivots.
The set of vectors in Step 2 is a basis for the range of L.
■
Example. Find a basis for the row space and for column space of the matrix
\[
{\bf A} = \left[ \begin{array}{cccccc} 1 &-3&4&-2&5&4 \\ 2 &-6&9 &-1&8&2 \\ 2&-6&9 &-1&9&7 \\ -1&3&-4&2&-5&-4 \end{array} \right] .
\]
Since elementary row operations do not change the row space of a matrix, we can find a basis for the row space of
A by finding a basis for the row space
of any row echelon form of
A. Reducing
A to Gaussian form, we obtain
\[
{\bf A} \, \sim \, {\bf R} = \left[ \begin{array}{cccccc} 1 &-3&4&-2&5&4 \\ 0 &0&1 &3&-2&-6 \\ 0&0&0 &0&1&5 \\ 0&0&0&0&0&0 \end{array} \right] .
\]
According to the above theorem, the nonzero row vectors of
R form a basis for the row space of
R and hence form a basis for the row space of
A. These basis vectors are
\begin{align*}
{\bf r}_1 &= \left[ 1, \ -3, \ 4,\ -2, \ 5, \ 4 \right] ,
\\
{\bf r}_2 &= \left[ 0, \ 0, \ 1,\ 3, \ -2, \ -6 \right] ,
\\
{\bf r}_3 &= \left[ 0, \ 0, \ 0,\ 0, \ 1, \ 5 \right]
\end{align*}
Keeping in mind that
A and
R can have different column spaces, we cannot find a basis for the column space of
A directly
from the column vectors of
R. However, we can determing them by identifying the corresponding column vectors of
A that form a basis for the column space.
Since the first, third, and fifth columns of
R contain the leading 1's of the row vectors, we claim that the vectors in these columns form the required basis:
\[
{\bf c}_1 = \left[ \begin{array}{c} 1 \\ 2 \\ 2 \\ -1 \end{array} \right] , \qquad {\bf c}_3 = \left[ \begin{array}{c} 4 \\ 9 \\ 9 \\ -4 \end{array} \right] , \qquad {\bf c}_5 = \left[ \begin{array}{c} 5 \\ 8 \\ 9 \\ -5 \end{array} \right] .
\]
Null Space or Kernel
If
A is an
\( m\times n \) matrix, then the solution space of the homogeneous system of algebraic equations
\( {\bf A}\,{\bf x} = {\bf 0} ,\) which is a subspace of
\( \mathbb{R}^n , \) is called the
null space or
kernel of matrix
A.
It is usually denoted by ker(
A). The null space of the adjoint matrix
\( {\bf A}^{\ast} = \overline{\bf A}^{\mathrm T} \) is
a subspace of
\( \mathbb{R}^m \) and is called the
cokernel of
A and denoted by coker(
A). ■
Theorem: Elementary row operations do not change the kernel and the row space of a matrix. ■
Theorem: Let \( L:\,V\, \mapsto \, U \) be a linear transformation.
The kernel of L is the subspace of V and the range of L is a subspace of U. ■
Theorem: If \( L:\,V\, \mapsto \, U \) is a linear transformation and V is
finite dimension, then
\[
\dim \left( \ker (L) \right) + \dim \left( \mbox{range}(L) \right) = \dim (V) .
\]
If
L is defined by an
m-by-
n matrix
A, which has the column space and row space to be of dimension
r, then the dimension of its kernel is
\( n-r \) and the dimension of its cokernel (which is left null space of
A or kernel of
\( {\bf A}^{\mathrm T} \) ) is
\( m-r .\) ■
Theorem: For a \( m\times n \) matrix, the kernel is the orthogonal complement of the row space in \( \mathbb{R}^n . \) ■
Theorem: For a \( m\times n \) matrix, the cokernel (the left null space) is the orthogonal complement of the column space in \( \mathbb{R}^m . \) ■
A Basis for the Kernel: If \( L:\,\mathbb{R}^n\, \mapsto \, \mathbb{R}^m \)
is a linear transformation given by \( L({\bf x}) = {\bf A}\,{\bf x} , \) for some
\( m \times n \) matrix A. To find a basis for ker(L), perform the following steps:
Step 1: Find B, the reduced row echelon form of A.
Step 2: Solve for oneparticular solution for each independent variable in the homogeneous system \( {\bf B}\,{\bf x} = {\bf 0} .\)
The ith such solution, \( {\bf v}_i , \) is found by setting the ith independent
variable equal to 1, and setting all other independent variables equal to 0.
The set \( \{ {\bf v}_1, \ {\bf v}_2 , \ \ldots , \ {\bf v}_k \} \) found in Step 2 is a basis for ker(L).
You may want to replace \( {\bf v}_i \) with \( c\,{\bf v}_i , \)
where \( c\ne 0 , \) to eliminate fractions. ■
Sage will compute a null space for us. Which is rather remarkable, as it is an infinite
set! Again, this is a powerful command, and there is lots of
associated theory, so we
will not understand everything about it right away, and it also has a radically different
name in Sage. But we will find it useful immediately. Lets reprise an example.
The relevant command to build the null space of a matrix is
.right_kernel(), where
again, we will rely exclusively on the “right” version. Also, to match our work in the
text, and make the results more recognizable, we will consistently us the keyword
option
basis=’pivot’
, which we will be able to explain once we have more theory. Note too, that this is a place where it is critical that
matrices are defined to use the rationals as their number system (QQ).
sage:I = matrix(QQ, [[ 1, 4, 0, -1, 0, 7, -9],
... [ 2, 8, -1, 3, 9, -13, 7],
... [ 0, 0, 2, -3, -4, 12, -8],
... [-1, -4, 2, 4, 8, -31, 37]])
sage: nsp = I.right_kernel(basis=’pivot’)
Vector space of degree 7 and dimension 4 over Rational Field
User basis matrix:
[-4 1 0 0 0 0 0]
[-2 0 -1 -2 1 0 0]
[-1 0 3 6 0 1 0]
[ 3 0 -5 -6 0 0 1]
As we said,
nsp
contains a lot of unfamiliar information. Ignore most of it for
now. But as a set, we can test membership in nsp:
sage: x = vector(QQ, [3, 0, -5, -6, 0, 0, 1])
sage: x in nsp
True
sage: y = vector(QQ, [-4, 1, -3, -2, 1, 1, 1])
sage: y in nsp
True
sage: z = vector(QQ, [1, 0, 0, 0, 0, 0, 2])
sage: z in nsp
False
We did a bad thing above, as Sage likes to use I
for the imaginary number
i (which is also denoted by
j) and we just clobbered that. We won’t do it again. See below how to fix this.
nsp is an infinite set. Since we know the null space is defined as solution to a system of
equations, and the work above shows it has at least two elements, we are not surprised
to discover that the set is infinite
sage: nsp.is_finite()
False
Note that in Sage, the kernel of a matrix
A is the “left kernel”, i.e. the space of vectors
z
such that
\( {\bf z}\,{\bf A} = {\bf 0} . \) This space is called cokernel of matrix A.
sage: A = Matrix([[1,2,3],[3,2,1],[1,1,1]])
sage: kernel(A)
Free module of degree 3 and rank 1 over Integer Ring
Echelon basis matrix:
[ 1 1 -4]
Example. Let \( L\,:\, \mathbb{R}^5 \mapsto \mathbb{R}^4 \) be given by
\( L[{\bf x}] = {\bf A}\,{\bf x} , \) where
\[
{\bf A} = \begin{bmatrix} 8&4&16&32&0 \\ 4&2&10&22&-4 \\ -2&-1&-5&-11&7 \\ 6&3&15&33&-7 \end{bmatrix} .
\]
To find the kernel of of the linear operator
L, we use Gauss-Jordan elimination
\[
{\bf A} \, \sim \, {\bf R} = \begin{bmatrix} 1& \frac{1}{2} & 0& -2&0 \\ 0&0&1&3&0 \\ 0&0&0&0&1 \\ 0&0&0&0&0 \end{bmatrix} .
\]
Since the pivots are in columns 1, 3, and 5, the corresponding variables
\( x_1 , \ x_3 , \ x_4 \) are leading avriables, and
\( x_2 , \ x_4 \) are free variables. Therefore, the system of algebraic equations
\( {\bf A}\,{\bf x} = {\bf 0} \) can be written as
\[
\begin{cases}
x_1 &= - \frac{1}{2}\, x_2 + 2\,x_4 , \\
x_3 &= - x_4 , \\
x_5 &= 0 . \end{cases}
\]
We construct two particular solutions, first by setting \( x_2 =1 \quad\mbox{and} \quad x_4 =0 \)
to obtain \( {\bf u}_1 = \left[ -1, 2, 0,0,0 \right]^{\mathrm T} , \) and then setting \( x_2 =0 \quad\mbox{and} \quad x_4 =1 ,\)
yielding \( {\bf u}_2 = \left[ 2, 0, -3, 1, 0 \right]^{\mathrm T} . \)
The set \( \left\{ {\bf u}_1 , {\bf u}_2 \right\} \) forms a basis for ker(L), and thus
\( \mbox{dim}(\mbox{ker}(L) = \mbox{dim}(\mbox{ker}({\bf A}) = 2, \) which equals the number of independent variables. The entire
subspace ker(L) consists of all linear combinations of the basis vectors.
■
Example. Consider 2-by-4 matrix of rank 2
\[
{\bf A} = \begin{bmatrix} 1&2&3&4 \\ 0&1&2&3 \end{bmatrix} .
\]
The vectors
\( {\bf u}_1 = \left[ 1,\ 2, \ 3, \ 4 \right] \) and
\( {\bf u}_2 = \left[ 0, \ 1,\ 2, \ 3 \right] \)
form the basis for the row space. To find the kernel of matrix
A, we need to solve the system of equations
\[
\begin{cases} x_1 + 2 x_2 + 3 x_3 + 4x_4 &=0, \\
x_2 + 2x_3 + 3x_4 &=0. \end{cases}
\]
Since
\( x_1 = x_3 + 2x_4 \) and
\( x_2 = -2x_3 -3 x_4 , \) we find the basis
of the null space (= kernel) of
A to be spanned on two vectors:
\[
{\bf u}_3 = \left[ 1, \ -2, \ 1, \ 0 \right]^{\mathrm T} , \qquad {\bf u}_4 = \left[ 2, \ -3, \ 0, \ 1 \right]^{\mathrm T} .
\]
These four vectors are a basis in
\( \mathbb{R}^4 . \) Any vector
\( {\bf x} = \left[ a, \ b, \ c,\ d \right]^{\mathrm T} \)
can be split into
\( {\bf x}_r \) in the row space and
\( {\bf x}_n \) in the kernel:
\begin{align*}
\begin{bmatrix} a \\ b \\ c \\ d \end{bmatrix} &= \frac{7\,a +4\,b +c -2\,d}{10} \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} +
\frac{-2\,a -b +d}{2} \begin{bmatrix} 0 \\ 1 \\ 2 \\ 3 \end{bmatrix}
\\
& \quad +
\frac{-a -2\,b + 7\, c -4\, d}{10} \begin{bmatrix} 1 \\ -2 \\ 1 \\ 0 \end{bmatrix} +
\frac{2\, a - b -4\,c +3\,d}{10} \begin{bmatrix} 2 \\ -3 \\ 0 \\ 1 \end{bmatrix} .
\end{align*}
This allows us to build projection matrices for the row space
\[
{\bf R} = \left[ {\bf u}_1 , \ {\bf u}_2 \right] \frac{1}{10} \begin{bmatrix} 7&4&1&-2 \\ -10&-5&0&5 \end{bmatrix} =
\frac{1}{10} \begin{bmatrix} 7&4&1&-2 \\ 4&3&2&1 \\ 1&2&3&4 \\ -2&1&4&7 \end{bmatrix}
\]
and for the null space (kernel)
\[
{\bf K} = \left[ {\bf u}_3 , \ {\bf u}_4 \right] \frac{1}{10} \begin{bmatrix} -1&-2&7&-4 \\ 2&-1&-4&3 \end{bmatrix} =
\frac{1}{10} \begin{bmatrix} 3&-4&-1&2 \\ -4&7&-2&-1 \\ -1&-2&7&-4 \\ 2&-1&-4&3 \end{bmatrix} .
\]
The eigenvalues of both matrices
R and
K are 1,1,0,0, so they are projection because
\( {\bf R}^2 = {\bf R} \)
and
\( {\bf K}^2 = {\bf K} . \) Moreover, these projection matrices are orthogonal because they are symmetric. These matrices are not defective; for instance,
the eigenvectors corresponding to double eigenvalue
\( \lambda_1 = 1 \) of matrix
K are
\( {\bf u}_1 = \left[ 2, \ -3, \ 0, \ 1 \right]^{\mathrm T} \) and
\( {\bf u}_2 = \left[ 1, \ -2, \ 1, \ 0 \right]^{\mathrm T} , \) while eigenvectors corresponding
to double eigenvalue
\( \lambda_2 = 0 \) are
\( {\bf u}_3 = \left[ 3, \ 2, \ 1, \ 0 \right]^{\mathrm T} \)
and
\( {\bf u}_4 = \left[ 2, \ 1, \ 0, \ -1 \right]^{\mathrm T} .\) Therefore, these two projection matrices
R and
K share the same minimal polynomial
\( \psi (\lambda ) = \lambda (\lambda -1) . \)
Multiplying A with its transpose, we get two symmetric square matrices
\[
{\bf A} \,{\bf A}^{\mathrm T} = \begin{bmatrix} 30 & 20 \\ 20 & 14 \end{bmatrix} \quad\mbox{with eigenvalues} \quad 22 \pm 4\sqrt{29} ,
\]
and
\[
{\bf A}^{\mathrm T} {\bf A} = \begin{bmatrix} 1&2&3&4 \\ 2&5&8&11 \\ 3&8&13&18 \\ 4&11&18&25 \end{bmatrix} \quad\mbox{with eigenvalues} \quad 22 \pm 4\sqrt{29} , \ 0, \ 0 .
\]
Matrices
A and
\( {\bf A}^{\mathrm T} {\bf A} \) have the same null space (= kernel).
Rank and Nullity
The common dimension of the row space and the column space of a matrix
A is called the
rank and is denoted by rank(
A);
the dimension of the kernel of
A is called the
nullity of
A and is denoted by nullity(
A).
Theorem: If A is a matrix with n columns, then rank(A) + nullity(A) = n. ■
Theorem: The rank of a matrix is the order of the largest nonzero determinant that can be obtained from the elements of the matrix. ■
Theorem: If A is a matrix with m rows, then rank(A) + nullity\( \left( {\bf A}^{\mathrm T} \right) =m. \) ■
Theorem: If A is an \( m \times n \) matrix, then
-
rank(A) = the number of leading variables or pivots in the general solution of \( {\bf A}\,{\bf x} = {\bf 0}. \)
-
rank(A) = the maximum number of linearly independent row vectors in A.
- nullity(A) = the number of parameters in the general solution of \( {\bf A}\,{\bf x} = {\bf 0}. \) ■
Theorem: If A is any matrix, then rank(A) = nullity(\( {\bf A}^{\mathrm T} ).\) ■
Theorem: Suppose that a linear system
\( {\bf A}\,{\bf x} = {\bf b} \) with m equations and n variables is consistent.
If the coefficient matrice A has the rank r, then the solution of the system contains \( n-r \) parameters. ■
Theorem: Every rank 1 matrix has the special form \( {\bf A} = {\bf u} \,{\bf v}^{\mathrm T} = \) column times row. ■
The columns are multipliers of
u. The rows are multipliers of
\( {\bf v}^{\mathrm T} .\)
The null space is the plane perpendicular to
v: (
\( {\bf A}{\bf x} = {\bf 0} \) means that
\( {\bf u}\left( {\bf v}^{\mathrm T} {\bf x} \right) = {\bf 0} \) and then
\( {\bf v}^{\mathrm T} {\bf x} = 0). \)
Example. Consider the system of linear algebraic equations
\[
\begin{split} x_1 + 3\,x_2 - 2\,x_3 &=-7 , \\
4\,x_1 + x_2 + 3\,x_3 &= 5, \\
2\,x_1 -5\,x_2 + 7\,x_3 &= 19. \end{split}
\]
Applicatying of Gauss-Jordan elimination procedure to the augmented matrix, we get
\[
\left( \begin{array}{ccc|c} 1 & 3 & -2 & -7 \\ 4&1&3&5 \\ 2&-5& 7 & 19 \end{array} \right) \qquad \Longrightarrow \qquad
\left( \begin{array}{ccc|c} 1 & 0 & 1 & 2 \\ 0&1&-1&-3 \\ 0&0&0&0 \end{array} \right) .
\]
Therefore, rank
\( ({\bf A} ) = \mbox{rank} \left( {\bf A} | {\bf b} \right) =2, \) and so the given system is consistent. With
\( n=3 , \) we see that the number of parameters in the solution is
\( 3-2 =1 . \) ■
Sage computes rank and nullity:
sage: M.rank()
sage: M.right_nullity()
Suppose that a matrix
M is partitioned into 2-by-2 blocks
\( {\bf M} = \begin{bmatrix} {\bf A} & {\bf B} \\ {\bf C} & {\bf D} \end{bmatrix} .\)
Then we immediately obtain the rank additivity formulas
\[
\mbox{rank}({\bf M} ) = \mbox{rank} ({\bf A} ) + \mbox{rank}\left( {\bf M} / {\bf A} \right) = \mbox{rank} ({\bf D} ) + \mbox{rank}\left( {\bf M} / {\bf D} \right) ,
\]
where Schur complements are
\[
\left( {\bf M} / {\bf A} \right) = {\bf D} - {\bf C}\,{\bf A}^{-1} {\bf B} \qquad \mbox{and} \qquad
\left( {\bf M} / {\bf D} \right) = {\bf A} - {\bf B}\,{\bf D}^{-1} {\bf C} .
\]
assuming that the indicated inverses exist.
Square Matrices
A very important class of matrices constitute so called square matrices that have the same number of rows as columns. In computer graphics, square matrices are used for transformations.
An n-by-n matrix is known as a square matrix of order n. Square matrices of the same order can be not only added, subtructed or multiplied by a constant, but also multiplied.
Theorem: If A is an \( n \times n \) matrix, then the following statements are equivalent.
-
A is invertible.
- \( {\bf A}\,{\bf x} = {\bf 0} \) has only the trivial solution.
-
The reduced row echelon form (upon application of Gauss--Jordan elimination) is the identity matrix.
- A has nullity/kernel 0. ■
- A has rank n.
- A is expressible as a product of elementary matrices.
- \( {\bf A}\,{\bf x} = {\bf b} \) is consistent for every \( n \times 1 \) matrix b.
- \( {\bf A}\,{\bf x} = {\bf b} \) has exactly one solution for every \( n \times 1 \) matrix b.
- \( \det ({\bf A} ) \ne 0 .\)
- \( \lambda =0 \) is not an eigenvalue of A.
- The row vectors of A span \( \mathbb{R}^n . \)
- The column vectors of A form a basis for \( \mathbb{R}^n . \)
Cramer's rule
While the following theorem is known as Cramer's rule; actually the Swiss mathematician Gabriel Cramer (1704--1752) is not the author of this statement.
Theorem: Let \( {\bf A}\,{\bf x} = {\bf b}\) be a system of \( n \)
equations in \( n \) variables. Let \( {\bf A}_i ,\) for
\( 1 \le i \le n ,\) be defined as the \( n \times n \) matrix
obtained by replacing the i-th column of A with b. Then, if \( \det {\bf A} \ne 0 ,\)
the entries of the unique solution x of \( {\bf A}\,{\bf x} = {\bf b}\) are given by
\[
x_1 = \frac{| {\bf A}_1 |}{| {\bf A} |} , \quad x_2 = \frac{| {\bf A}_2 |}{| {\bf A} |} , \quad \ldots , \quad x_n = \frac{| {\bf A}_n |}{| {\bf A} |} .
\]
We demonstrate how Sage can solve the system of algebraic equations using Cramer's rule.
sage: A=matrix(QQ,3,3,[[1,-4,1],[4,-1,2],[2,2,-3]]);A
[ 1 -4 1]
[ 4 -1 2]
[ 2 2 -3]
sage: b=vector([6,-1,-20])
sage: B=copy(A)
sage: C=copy(A)
sage: D=copy(A)
sage: B[:,0] = b
sage: C[:,1] = b
sage: D[:,2] = b
sage: x1=B.det()/A.det(); x1
-144/55
sage: x2=C.det()/A.det(); x2
-61/55
sage: x3=D.det()/A.det(); x3
46/11
Symmetric and self-adjoint matrices
As usual, we denote by \( {\bf A}^{\ast} \) the complex conjugate and transposed matrix to the square matrix A,
so \( {\bf A}^{\ast} = \overline{{\bf A}^{\mathrm T}} . \)
If a matrix A has real entries, then its adjoint \( {\bf A}^{\ast} \) is just transposed \( {\bf A}^{\mathrm T} . \)
Hermitian matrices are named after a French mathematician Charles Hermite (1822--1901), who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of always having real eigenvalues. Some
properities of self-adjoint matrices.
-
All eigenvalues of a self-adjoint (Hermitian) matrix are real. Eigenvectors corresponding to different eigenvalues are linearly independent.
- A self-adjoint matrix is not defective; this means that algebraic multiplicity of every eigenvalue is equal to its geometric multiplicity.
- The entries on the main diagonal (top left to bottom right) of any Hermitian matrix are necessarily real, because they have to be equal to their complex conjugate.
- Every self-adjoint matrix is a normal matrix.
- The sum of any two Hermitian matrices is Hermitian.
- The inverse of an invertible Hermitian matrix is Hermitian as well.
- The product of two Hermitian matrices A and B is Hermitian if and only if
\( {\bf A}{\bf B} = {\bf B}{\bf A} . \) Thus \( {\bf A}^n \)
is Hermitian if A is self-adjoint and n is an integer.
- For an arbitrary complex valued vector v the product \( \left\langle {\bf v}, {\bf A}\, {\bf v} \right\rangle = {\bf v}^{\ast} {\bf A}\, {\bf v} \) is real.
- The sum of a square matrix and its conjugate transpose \( {\bf A} + {\bf A}^{\ast} \)
is Hermitian.
- The determinant of a Hermitian matrix is real.
Recall that an \( n \times n \) matrix P is said to be orthogonal if \( {\bf P}^{\mathrm{T}} {\bf P} = {\bf P} {\bf P}^{\mathrm{T}} = {\bf I} , \)
the identity matrix; that is, if P has inverse \( {\bf P}^{\mathrm{T}} . \)
A nonsingular square complex matrix A is unitary if and only if \( {\bf A}^{\ast} = {\bf A}^{-1} . \)
Example. The matrix
\[
{\bf P} = \begin{pmatrix} 3/5 & 4/5 \\ -4/5 & 3/5 \end{pmatrix}
\]
is orthogonal. On the other hand, the matrix
\[
{\bf A} = \begin{pmatrix} \frac{1-{\bf j}}{\sqrt{3}} & 0 & \frac{\bf j}{\sqrt{3}} \\
\frac{-1+{\bf j}}{\sqrt{15}} & \frac{3}{\sqrt{15}} & \frac{2{\bf j}}{\sqrt{15}} \\
\frac{1-{\bf j}}{\sqrt{10}} & \frac{2}{\sqrt{10}} & \frac{-2{\bf j}}{\sqrt{10}} \end{pmatrix}
\]
is unitary. Here
j is a unit vector in positive vertical direction on the complex plane, so
\( {\bf j}^2 = -1 . \)
sage: P*u1
sage: P*u2
sage: P*u3
Theorem: A matrix is orthogonal if and only if, as vectors, its columns are pairwise orthogonal. ■
Theorem: An \( n \times n \) matrix is orthogonal if and only if its columns form an orthnormal basis of
\( \mathbb{R}^n . \) ■
A square matrix A is said to be orthogonally diagonalisable if there exists an orthogonal matrix P such that
\( {\bf P}^{\mathrm{T}} {\bf A} {\bf P} = {\bf \Lambda} , \) where Λ is a diagonal matrix (of eigenvalues).
If P in the above equation is an unitary complex matrix, then we call A unitary diagonalizable. ■
Theorem: An \( n \times n \) matrix A is orthogonally diagonalisable if and only if A is symmetric.
■
Theorem: An \( n \times n \) matrix A is unitary diagonalisable if and only if A is normal.
■
Example. We show that the following symmetric (but not self-adjoint) matrix is unitarity diagonalizable:
\[
{\bf A} = \begin{bmatrix} -4+5{\bf j} & 2+ 2{\bf j} & 1-2 {\bf j} \\ 2+ 2{\bf j} & -1+8{\bf j} & -2-2{\bf j} \\
4+4{\bf j} & -2-2{\bf j} & -4+5{\bf j}
\end{bmatrix} ,
\]
where
j is a unit vector in vertical direction on the complex plane
\( \mathbb{C} , \) so
\( {\bf j}^2 = -1 . \)
First, we check that matrix
A is normal:
Then we find its eigenvalues and eigenvectors
Out of these eigenvectors, we build the matrix
S, column by column:
Finally, we verify that
\( {\bf S}^{\ast} {\bf A} {\bf S} = {\bf \Lambda} , \) where
Λ is the
diagonal mutrix of eigenvalues.
Orthogonalization of a symmetric matrix: Let A be a symmetric real \( n\times n \) matrix.
Step 1: Find an ordered orthonormal basis B for \( \mathbb{R}^n ;\) you can use the standard basis for \( \mathbb{R}^n .\)
Step 2: Find all the eigenvalues \( \lambda_1 , \lambda_2 , \ldots , \lambda_s \) of A.
Step 3: Find basis for each eigenspace of A.
Step 4: Perform the Gram--Schmidt process on the basis for each eigenspace. Normalize to get an orthonormal basis C.
Step 4: Build the transition matrix S from C, which is an orthogonal matrix and \( {\bf \Lambda} = {\bf S}^{-1} {\bf A} {\bf S} . \)
Example. Consider a symmetric matrix
\[
{\bf A} = \frac{1}{7} \begin{bmatrix} 15&-21&-3&-5 \\
-21&35&-7&0 \\ -3&-7&23&15 \\ -5&0&15& 39 \end{bmatrix} .
\]
Its characteristic polynomial
\( \chi (\lambda ) = \det \left( \lambda {\bf I} - {\bf A} \right) \)
has three distinct roots
\( \lambda = 0, 2, 7 \) (double), as Sage confirms:
sage: A =
sage: A.eigenvalues()
sage: A.fcp()
Solving appropriate homogeneous equations, we determine eigenvectors:
\begin{align*}
E_{0} &= \left\{ \left[ 3, 2, 1, 0 \right] \right\} , \\
E_{2} &= \left\{ \left[ 1, 0, -3, 2 \right] \right\} , \\
E_7 &= \left\{ \left[ -2,3,0,1 \right] , \quad \left[ 3,-5,1,0 \right] \right\} .
\end{align*}
Since eigenspaces for corresponding to eigenvalues
\( \lambda =0 \quad\mbox{and}\quad \lambda =2 \) are one dimensional,
we just divide the corresponding eigenvectors by their norms. This yields orthonormal basis:
\begin{align*}
E_{0} &= \left\{ \frac{1}{\sqrt{14}} \left[ 3, 2, 1, 0 \right] \right\} , \\
E_{2} &= \left\{ \frac{1}{\sqrt{14}} \left[ 1, 0, -3, 2 \right] \right\} . \\
\end{align*}
Performing Gram--Schmidt orthogonalizing procedure, we get
\[
E_7 = \left\{ \frac{1}{\sqrt{14}} \left[ -2,3,0,1 \right] , \quad \frac{1}{\sqrt{14}} \left[ 0,-1, 2, 3 \right] \right\} .
\]
This allows us to construct the transition matrix and the diagonal matrix of eigenvalues:
\[
{\bf S} = \frac{1}{\sqrt{14}} \begin{bmatrix} 3&1&-2&0 \\ 2&0&3&-1 \\ 1&-3&0&2 \\ 0&2&1&3 \end{bmatrix} , \quad {\bf \Lambda} = \begin{bmatrix} 0&0&0&0 \\ 0&2&0&0 \\ 0&0&7&0 \\ 0&0&0&7 \end{bmatrix} .
\]
Cholesky decomposition
Every symmetric, positive definite matrix
A can be decomposed into a product of a unique lower triangular matrix
L and its transpose:
\[
{\bf A} = {\bf L} \, {\bf L}^{\ast} ,
\]
where
\( {\bf L}^{\ast} = \overline{\bf A}^{\mathrm T} \) denotes the conjugate transpose of
L.
The matrix
L is called the Cholesky factor of
A, and can be interpreted as a
generalized square root of
A, as described in Cholesky decomposition or Cholesky factorization.
It was discovered by a French military officer and mathematician André-Louis Cholesky (1875--1918) for real matrices. When it is applicable, the Cholesky decomposition
is roughly twice as efficient as the LU decomposition for solving systems of linear equations
If the matrix A is Hermitian and positive semi-definite, then it still has a decomposition of the form \( {\bf A} = {\bf L}{\bf L}^{\ast} \)
if the diagonal entries of L are allowed to be zero.
When A has real entries, L has real entries as well and the factorization may
be written \( {\bf A} = {\bf L}{\bf L}^{\mathrm T} . \)
The Cholesky decomposition is unique when A is positive definite; there is only one lower
triangular matrix L with strictly positive diagonal entries such that \( {\bf A} = {\bf L}{\bf L}^{\mathrm T} . \)
However, the decomposition need not be unique when A is positive semidefinite.
A closely related variant of the classical Cholesky decomposition is the LDL decomposition,
\[
{\bf A} = {\bf L} \, {\bf \Lambda}\,{\bf L}^{\ast} ,
\]
where
L is a lower unit triangular (unitriangular) matrix and
\( \Lambda \) is a diagonal matrix.
The LDL variant, if efficiently implemented, requires the same space and computational complexity to construct
and use but avoids extracting square roots. Some indefinite matrices for which no Cholesky decomposition exists have
an LDL decomposition with negative entries in \( \Lambda . \) For these reasons, the
LDL decomposition may be preferred.
Example.
Here is the Cholesky decomposition of a symmetric real matrix:
\[
\begin{bmatrix} 4&12&-16 \\ 12&37&-43 \\ -16&-43&93
\end{bmatrix} = \begin{bmatrix} 2&0&0 \\ 6&1&0 \\ -8&5&3 \end{bmatrix} \begin{bmatrix} 2&6&-8 \\ 0&1&5 \\ 0&0&3 \end{bmatrix} .
\]
And here is its
\( {\bf L}{\bf \Lambda}{\bf L}^{\mathrm T} \) decomposition:
\[
\begin{bmatrix} 4&12&-16 \\ 12&37&-43 \\ -16&-43&93
\end{bmatrix} = \begin{bmatrix} 1&0&0 \\ 3&1&0 \\ -4&5&1 \end{bmatrix} \begin{bmatrix} 4&0&0 \\ 0&1&0 \\ 0&0&9 \end{bmatrix}
\begin{bmatrix} 1&3&-4 \\ 0&1&5 \\ 0&0&1 \end{bmatrix} .
\]
The Cholesky decomposition is mainly used for the numerical solution of linear equations
\( {\bf A}{\bf x} = {\bf b} . \)
■
The Cholesky algorithm, used to calculate the decomposition matrix L, is a modified version of Gaussian elimination.
The Cholesky–Banachiewicz and Cholesky–Crout algorithms
are based on rewriting the equation \( {\bf A} = {\bf L}{\bf L}^{\ast} \) as
\[
{\bf A} = {\bf L} {\bf L}^{\mathrm T} = \begin{bmatrix} L_{11} & 0&0 \\ L_{21}&L_{22} &0 \\ L_{31} & L_{32} & L_{33}\end{bmatrix}
\begin{bmatrix} L_{11}& L_{21}& L_{31} \\ 0&L_{22} & L_{32} \\ 0&0&L_{33} \end{bmatrix} =
\begin{bmatrix} L_{11}^2 &L_{21} L_{11}&L_{31} L_{11} \\ L_{21} L_{11} &L_{21}^2 L_{22}^2 & L_{31} L_{21} +L_{32} L_{22} \\ L_{31} L_{11} & L_{31} L_{21} +L_{32} L_{22} & L_{31}^2 + L_{32}^2 + L_{33}^2 \end{bmatrix} ,
\]
which leads to
\begin{align*}
L_{j,j} &= \sqrt{A_{j,j} - \sum_{k=1}^{j-1} L_{j,k} L_{j,k}^{\ast}} ,
\\
L_{i,j} &= \frac{1}{L_{j,j}} \left( A_{i,j} - \sum_{k=1}^{j-1} L_{i,k} L_{j,k}^{\ast} \right) , \quad i>j.
\end{align*}
So we can compute the
(i, j) entry if we know the entries to the left and above. The computation is usually arranged in either of the following orders
-
The Cholesky–Banachiewicz algorithm starts from the upper left corner of the matrix L and proceeds to calculate the matrix row by row.
- The Cholesky–Crout algorithm starts from the upper left corner of the matrix L and proceeds to calculate the matrix column by column.
Example. Consider the positive definite matrix
\[
{\bf A} = \begin{bmatrix} 2&1&1 \\ 1&2&1 \\ 1&1&2 \end{bmatrix} .
\]
Using the Cholesky–Banachiewicz algorithm, we construct the lower triangular matrix
L:
\[
L_{1,1} = \sqrt{2}, \quad L_{2,1} = L_{3.1} = \frac{1}{\sqrt{2}} , \quad L_{2,2} = \sqrt{\frac{3}{2}}, \quad L_{3,2} = \frac{1}{\sqrt{6}} , \quad L_{3,3} = \frac{2}{\sqrt{3}} .
\]
We verify with Sage that
\( {\bf L} \,{\bf L}^{\mathrm T} = {\bf A} : \)
sage: A =
sage: A.eigenvalues()
sage: A.fcp()
Projection Operators
A projection is a linear transformation P (or matrix P corresponding to this transformation
in an appropriate basis) from a vector space to itself
such that \( P^2 = P. \) That is, whenever P is applied twice to any vector, it
gives the same result as if it were applied once (idempotent). In what follows, we ignore the trivial cases of the
identity transformation (matrix) and zero transformation; therefore, we consider only projections of a finite
dimensional vector space into its nonzero subspace. The spectrum (all eigenvalues) of a projection matrix consists
of zeroes and ones because its resolvent is
\[
\left( \lambda {\bf I} - {\bf P} \right)^{-1} = \frac{1}{\lambda} \,{\bf I} + \frac{1}{\lambda (\lambda -1)} \, {\bf P} .
\]
Any nontrivial projection
\( P^2 = P \) on a vector space of dimension
n is represented by a
diagonalizable matrix having minimal polynomial
\( \psi (\lambda ) = \lambda^2 - \lambda = \lambda \left( \lambda -1 \right) , \)
which is splitted into product of distinct linear factors.
For subspaces U and W of a vector space V, the sum of U and W, written
\( U + W , \) is simply the set of all vectors in V which are obtained by adding together a vector in U and a vector in W.
A sum of two subspaces \( U + W \) is said to be a direct sum if \( U \cap W = \left\{ {\bf 0} \right\} . \)
The direct sum of two subspaces is denoted as \( U \oplus W . \)
Theorem: The sum of two subspaces U and W is direct if and only if every vector z in the sum can be written uniquely (that is, in one way only) as \( {\bf z} = {\bf u} + {\bf w} , \)
where \( {\bf u} \in U \) and \( {\bf w} \in W . \)
■
The orthogonal complement of a subset S of a vector space V with inner product \( \langle {\bf x} , {\bf y} \rangle \) is
\[
S^{\perp} = \{ {\bf v} \in V \, : \quad \langle {\bf v} , {\bf s} \rangle =0 \ \mbox{ for all } {\bf s} \in S \}
\]
Subspaces
V and
U are orthogonal if every
v in
V is orthogonal to every
u in
U.
On the other hand,
V and
U are ``orthogonal complements'' if
U contains
all vectors perpendicular to
V
(and vice versa). Inside
\( \mathbb{R}^n , \) the dimensions of
V and
U add to
n.
When P projects onto one subspace, \( {\bf I} - {\bf P} \) projects onto the perpendicular subspace.
Theorem: For any subset S of a vector space V with inner product,
\( S^{\perp} \) is a subspace of V.
■
Theorem: For any subspace S of a finite-dimensional inner product space V,
then \( V= S \oplus S^{\perp} . \)
■
Theorem: A projection is orthogonal if and only if it is self-adjoint.
■
Suppose that a finite dimensional vector space V can be written as a direct sum of two subspaces U
and W, so \( V = U\oplus W . \) This means that each vector v from
V there is a unique \( {\bf u} \in U \) and a unique \( {\bf w} \in W \)
such that \( {\bf v} = {\bf u}+{\bf w} . \) This allows one to define two functions
\( P_U \, : \, V\mapsto U \) and \( P_W \, : \, V\mapsto W \)
as follows: for each \( {\bf v} \in V \) , if \( {\bf v} = {\bf u}+{\bf w} \)
where \( {\bf u} \in U \) and \( {\bf w} \in W , \) then let
\( P_U ({\bf v}) = {\bf u} \) and \( P_W ({\bf v}) = {\bf w} . \)
The mapping \( P_U \) is called the projection of V onto U, parallel to
W. The mapping \( P_W \) is called the projection of V onto W,
parallel to U. Then the subspaces U and W are the range and kernel of
\( P_U \) and \( P_W ,\) respectively.
When the vector space V has an inner product and is complete (is a Hilbert space) the concept of orthogonality
can be used. An orthogonal projection is a projection for which the range U and the null space
W are orthogonal subspaces. Thus, for every x and y in V
\[
\left\langle {\bf x} , {\bf P} {\bf y} \right\rangle = \left\langle {\bf P} {\bf x} , {\bf P} {\bf y} \right\rangle = \left\langle {\bf P} {\bf x} , {\bf y} \right\rangle = \left\langle {\bf x} , {\bf P}^{\ast} {\bf y} \right\rangle .
\]
Thus, there exists a basis in which
P
(more precisely, the corresponding orthogonal projection matrix
P) has the form
\[
{\bf P} = {\bf I}_r \oplus {\bf 0}_{n-r} ,
\]
where
r is the rank of
P. Here
\( {\bf I}_r \) is the identity
matrix of size
r, and
\( {\bf 0}_{n-r} \) is the zero matrix of size
n-r. ■
The term oblique projections is sometimes used to refer to non-orthogonal projections.
Example.
A simple example of a non-orthogonal (oblique) projection is
\[
{\bf P} = \begin{bmatrix} 0&0 \\ 1&1 \end{bmatrix} \qquad \Longrightarrow \qquad {\bf P}^2 = {\bf P} .
\]
The eigenvalues of lower triangular matrix P are \( \lambda_1 =1 \ \mbox{ and } \ \lambda_2 =0, \)
with corresponding eigenvectors \( {\bf u}_1 = \left[ 0,\ 1 \right]^{\mathrm T} \) and \( {\bf u}_2 = \left[ -1,\ 1 \right]^{\mathrm T} .\)
The range of matrix P is spanned on the vector \( {\bf u}_1 \) and the kernel is spanned on the eigenvector \( {\bf u}_2 . \) Since these two eigenvectors are not orthogonal, \( \langle {\bf u}_1 , {\bf u}_2 \rangle = 1, \)
the projection matrix P is oblique. On the other hand, the matrix
\[
{\bf P} = \begin{bmatrix} 1&0&0 \\ 0&0&0 \\ 0&0&1 \end{bmatrix}
\]
defines an orthogonal projection. ■
If the vector space is complex and equipped with an inner product, then there is an orthonormal basis in which an
arbitrary non-orthogonal projection matrix P is
\[
{\bf P} = \begin{bmatrix} 1& \sigma_1 \\ 0&0 \end{bmatrix} \oplus \cdots \oplus \begin{bmatrix} 1& \sigma_k \\ 0&0 \end{bmatrix} \oplus {\bf I}_m \oplus {\bf 0}_s ,
\]
where
\( \sigma_1 \ge \sigma_2 \ge \ldots \ge \sigma_k >0 . \) The integers
k,
s,
m,
and the real numbers
\( \sigma_i \) are uniquely determined. Note that
2k+s+m=n. The factor
\( {\bf I}_m \oplus {\bf 0}_s \) corresponds to the maximal
invariant subspace on which
P acts as an orthogonal projection (so that
P itself
is orthogonal if and only if
k = 0) and the
\( \sigma_i \) -blocks correspond to
the oblique components. ■
An orthogonal projection is a bounded operator. This is because for every v in the vector space
we have, by Cauchy--Bunyakovsky--Schwarz inequality:
\[
\| {\bf P} \,{\bf v}\|^2 = \left\langle {\bf P}\,{\bf v} , {\bf P}\,{\bf v} \right\rangle = \left\langle {\bf P}\,{\bf v} , {\bf v} \right\rangle \le \| {\bf P}\,{\bf v} \| \, \| {\bf v} \| .
\]
Thus,
\( \| {\bf P} \,{\bf v}\| \le \| {\bf v} \| . \) ■
All eigenvalues of an orthogonal projection are either 0 or 1, and the corresponding matrix is a singular one
unless it either maps the whole vector space onto itself to be the identity matrix or maps the vector space into
zero vector to be zero matrix; we do not consider these trivial cases. ■
Let us start with a simple case when the orthogonal projection is onto a line. If u is a unit vector on the
line, then the projection is given by the outer product:
\[
{\bf P}_{\bf u} = {\bf u}\,{\bf u}^{\mathrm T} .
\]
If
u is complex-valued, the transpose
\( {\bf u}^{\mathrm T} \) in the
above equation is replaced by an adjoint
\( {\bf u}^{\ast} .\) If
u is
not of unit length, then
\[
{\bf P}_{\bf u} = \frac{{\bf u}\,{\bf u}^{\mathrm T}}{\| {\bf u} \|^2} .
\]
This operator leaves
u invariant, and it annihilates all vectors orthogonal to
u,
proving that it is indeed the orthogonal projection onto the line containing
u.
A simple way to see this is to consider an arbitrary vector
x as the sum of a component on the line
(i.e. the projected vector we seek) and another perpendicular to it,
\( {\bf x} = {\bf x}_{\|} + {\bf x}_{\perp} , \)
where
\( {\bf x}_{\|} = \mbox{proj}_{\bf u} ({\bf x}) \) is the projection on the line spanned by
u.
Applying projection, we get
\[
{\bf P}_{\bf u} {\bf x} = {\bf u}\,{\bf u}^{\mathrm T} {\bf x}_{\|} + {\bf u}\,{\bf u}^{\mathrm T} {\bf x}_{\perp} =
{\bf u} \left( \mbox{sign} \left( {\bf u}^{\mathrm T} \, {\bf x}_{\|} \right) \left\| {\bf x}_{\|} \right\|\right) + {\bf u} \cdot 0 = {\bf x}_{\|}
\]
by the properties of the dot product of parallel and perpendicular vectors. The projection matrix
\( {\bf P}_{\bf u} \)
in
n-dimensional space has eigenvalue
\( \lambda_1 =0 \) of algebraic and geometrical multiplicity
n-1 with eigenspace
\( {\bf u}^{\perp} \) and another simple eigenvalue
\( \lambda_2 =1 \)
with eigenspace spanned on the vector
u.
Example.
Project \( {\bf x} = \left[ 1, \ 1, \ 1 \right]^{\mathrm T} \) onto \( {\bf a} = \left[ 1, \ 2, \ 3 \right]^{\mathrm T} . \)
First, we calculate \( {\bf x} \cdot {\bf a} = 1+2+3 =6 \) and \( \| {\bf a} \| = {\bf a} \cdot {\bf a} = 1+4+9 =14 . \)
Then we find the orthogonal projection matrix:
\[
{\bf P}_{\bf a} = \frac{{\bf a} \, {\bf a}^{\mathrm T}}{{\bf a}^{\mathrm T} {\bf a}} = \frac{{\bf a} \otimes {\bf a}}{{\bf a}^{\mathrm T} {\bf a}} =
\frac{1}{14} \, \begin{bmatrix} 1&2&3 \\ 2&4&6 \\ 3&6&9 \end{bmatrix} .
\]
This matrix projects any vector
x onto
a. We check
\( {\bf x}_{\|} = {\bf P} \,{\bf x} \)
for the particular
\( {\bf x} = \left[ 1, \ 1, \ 1 \right]^{\mathrm T} : \)
\[
{\bf x}_{\|} = {\bf P}_{\bf a} {\bf x} = \frac{1}{14} \, \begin{bmatrix} 1&2&3 \\ 2&4&6 \\ 3&6&9 \end{bmatrix} \, \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix} =
\frac{3}{7} \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} .
\]
If the vector
a is doubled, the matrix
P stays the same. It still projects onto the same line. If the matrix is squared,
\( {\bf P}_{\bf a}^2 = {\bf P}_{\bf a} . \) So projecting a second time doesn't change anything.
The diagonal entries of
\( {\bf P}_{\bf a} \) add up to 1. This matrix has eigenvalues 1, 0, 0.
The error vector between x and \( \mbox{proj}_{\bf a} ({\bf x}) = {\bf x}_{\|} \) is
\( {\bf x}_{\perp} = {\bf x} - {\bf x}_{\|} = \frac{1}{7} \left[ 4, \ 1,\ -2 \right]^{\mathrm T} .\)
These vectors \( {\bf x}_{\perp} \) and \( {\bf x}_{\|} \) will add to x.
From the geometrical point of view,
\[
{\bf x}_{\|} = \frac{{\bf a}^{\mathrm T} {\bf x}}{{\bf a}^{\mathrm T} {\bf a}} \,{\bf a} = {\bf P}_{\bf a} {\bf x} \quad \Longrightarrow \quad
\left\| {\bf x}_{\|} \right\| = \| {\bf x} \| \,\cos \theta .
\]
This allows us to find the cosine of the angle θ between these two vectors
x and
a:
\[
\cos\theta = \frac{\| {\bf x}_{\|} \|}{\| {\bf x} \|} = \frac{\sqrt{2}}{\sqrt{21}} \approx 0.3086 .
\]
We check
\( {\bf x}_{\perp} \perp {\bf a} . \)
Finally, we verify that both projection matrices, \( {\bf P}_{\bf a} \) and
\( {\bf P}^{\perp} = {\bf I} - {\bf P}_{\bf a} \) satisfy the property that the length squared of
ith column always equals to the ithe diagonal entry \( p_{i,i} \) . For instance,
\[
{\bf P}^{\perp} = \frac{1}{14} \begin{bmatrix} 13 & -2 & -3 \\ -2&10&-6 \\ -3&-6&5 \end{bmatrix} \qquad \Longrightarrow \qquad
p_{2,2} = \frac{10}{14} = \frac{4}{14^2} + \frac{100}{14^2} + \frac{36}{14^2} .
\]
The eigenvalues of the orthogonal projection
\( {\bf P}^{\perp} \) are 1, 1, 0.
Example.
Suppose that \( V= \mathbb{R}^3 \) with the standard inner product and suppose that S
is spanned on the vector \( {\bf u} = [\, 1, 2, 3 \,]^{\mathrm{T}} . \) Then \( S^{\perp} \)
is the set of all vectors v such that \( {\bf v} \perp {\bf s} \) for all
\( {\bf s} \in S . \) Now, any member of S is of the form \( \alpha {\bf u} , \)
where α is a real constant. We have \( \langle {\bf v} , \alpha {\bf u} \rangle = \alpha \langle {\bf v} , {\bf u} \rangle , \)
so \( {\bf v} = [ x, y, z ]^{\mathrm{T}} \) is in \( S^{\perp} \) precisely when,
for all α , \( \alpha \langle {\bf v} , {\bf u} \rangle =0 , \) which means
\( \langle {\bf v} , {\bf u} \rangle =0 . \) Therefore,
\[
S^{\perp} = \left\{ \begin{pmatrix} x \\ y \\ z \end{pmatrix} \ \vert \ x+ 2y + 3z =0 \right\} .
\]
That is,
S is the line through the origin in the direction of
u and
\( S^{\perp} \)
is the plane through the origin perpendicular to this line; that is, with normal vector
u.
To find the basis for
\( S^{\perp} , \) we solve the equation
\( x+2y+3z=0 \) to obtain
\( x= -2y-3z . \) So we have two-dimensional plane:
\[
S^{\perp} = \left\{ \begin{pmatrix} -2y -3z \\ y \\ z \end{pmatrix} = y \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix} + z \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix} \right\} .
\]
Therefore,
\( S^{\perp} \) is spanned on two vectors
\[
{\bf u}_1 = \left[ -2, 1, 0 \right]^{\mathrm T} \quad \mbox{and} \quad {\bf u}_2 = \left[ -3, 0, 1 \right]^{\mathrm T} .
\]
To build a projection matrix on
\( S^{\perp} , \) we make a 3-by-2 matrix of these vectors
\[
{\bf B} = \begin{bmatrix} -2&-3 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} , \quad \mbox{with} \quad {\bf B}^{\mathrm T} = \begin{bmatrix} -2&1&0 \\ -3 & 0 & 1 \end{bmatrix} .
\]
Then the projection matrix becomes
\[
{\bf P} = {\bf B} \left( {\bf B}^{\mathrm T} {\bf B} \right)^{-1} {\bf B}^{\mathrm T} = \frac{1}{14}
\begin{bmatrix} 13&-2&-3 \\ -2 & 10& -6 \\ -3 & -6&5 \end{bmatrix} .
\]
Its eigenvalues are 1,1,0, and
\( {\bf P}^2 = {\bf P} , \) so it is indeed a projection.
■
Theorem: Suppose that A is an \( m\times n \) real matrix.
Then the orthogonal complement of the column space (= range of the matrix A) in \( \mathbb{R}^m \) is the kernel of the transpose matrix, that is,
\( \mbox{Range}({\bf A})^{\perp} = \mbox{cokernel}({\bf A}) = \mbox{kernel} \left( {\bf A}^{\mathrm T} \right) , \) and the orthogonal complement of the null space (= kernel of the matrix A)
in \( \mathbb{R}^n \) is the
row space of the matrix, namely, \( \mbox{kernel}({\bf A})^{\perp} = \mbox{Row}({\bf A}) . \)
■
Theorem: If A is an \( m\times n \) matrix of rank n, then
\( {\bf A}^{\mathrm T} {\bf A} \) is invertible and symmetric.
■
A matrix is full row rank when each of the rows of the matrix are linearly independent and full column rank when
each of the columns of the matrix are linearly independent. For a square matrix these two concepts are equivalent
and we say the matrix is full rank if all rows and columns are linearly independent. A square matrix is full rank if
and only if its determinant is nonzero. The above theorem is referred to a full column rank matrix.
Theorem: A linear transformation T is a projection if and only if it is an idempotent, that is,
\( T^2 = T . \)
■
Theorem: Suppose that A is an \( m\times n \) real matrix
of rank n (full column rank). Then the matrix \( {\bf P} = {\bf A} \left( {\bf A}^{\mathrm T} {\bf A} \right)^{-1} {\bf A}^{\mathrm T} \)
represents the orthogonal projection of \( \mathbb{R}^m \) onto the range
of A.
■
Note that if
A is not a full column rank matrix, then
\( {\bf A}^{\mathrm T} {\bf A} \) is not invertible. Thus, we get
another criterion for consistency of the linear algebraic equation
\( {\bf A} {\bf x} = {\bf b} : \)
\[
{\bf P} {\bf b} = {\bf b} ,
\]
where
P is the projection operator on the column space of an
\( m\times n \) real matrix. ■
Example.
Consider the linear system \( {\bf A} {\bf x} = {\bf b} , \) where
\[
{\bf A} = \begin{bmatrix} -1&1&3&-6&8&-2 \\ -3&5&3&1&4&8 \\ 1&-3&3&-13&12&-12 \\ 0&2&-6&19&-20&14 \\ 5&13&-21&3&11&6
\end{bmatrix}, \quad {\bf b} = \begin{bmatrix} 0\\ 1\\ 2\\ 3\\ 4
\end{bmatrix} .
\]
Application of Gauss-Jordan elimination procedure yields
\[
{\bf R} = \begin{bmatrix} 8&0&0&-74&87&58 \\ 0&16&0&-46&71&-18 \\ 0&0&24&-99&231/2 & -65 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \end{bmatrix} .
\]
Since pivots are in the first three columns, the range (or column space) of the matrix
A is spanned
on the first three columns. Therefore, we build a full column rank matrix:
\[
{\bf B} = \begin{bmatrix} -1&1&3 \\ -3&5&3 \\ 1&-3&3 \\ 0&2&-6 \\ 5&13&-21 \end{bmatrix} .
\]
Then we define the orthogonal projection operator on range of the matrix
A:
\[
{\bf P} = {\bf B} \left( {\bf B}^{\mathrm T} {\bf B} \right)^{-1} {\bf B}^{\mathrm T} = \frac{1}{17}
\begin{bmatrix} 3&5&1&-4&0 \\ 5&14&-4&-1&0 \\ 1&-4&6&-7&0 \\ -4&-1&-7&11&0 \\ 0&0&0&0&1 \end{bmatrix} .
\]
Application of the projection matrix
P to the vector
b, we get
\[
{\bf P} {\bf b} = \frac{1}{17} \left[ -5, 3, -13, 18, 68 \right]^{\mathrm T} \ne {\bf b} .
\]
Therefore, the given system of equations
\( {\bf A} {\bf x} = {\bf b} , \) is inconsistent.
Now we check that the symmetric matrix P is a projector. First, we verify that it is idempotent:
Then we check its eigenvalues:
Since they are
\( \lambda = 1,1,1,0,0 , \) we conclude that
P is indeed the projector.
sage: P*u1
sage: P*u2
sage: P*u3
Now we use another approach: we find the basis for cokernel. To determine it, we transpose the given matrix and apply Gauss-Jordan elimination:
\[
{\bf A}^{\mathrm T} = \begin{bmatrix} -1&-3&1&0&5 \\ 1&5&-3&2&13 \\ 3&3&3&-6&21 \\ -6&1&-13&12&-12 \\ 8&4&12&-20&11
\\ -2&8&-12&14&6
\end{bmatrix} \quad \Longrightarrow \quad {\bf R} = \begin{bmatrix} 1&0&2&-3&0 \\ 0&1&-1&1&0 \\ 0&0&0&0&1 \\ 0&0&0&0&0
\\ 0&0&0&0&0 \\ 0&0&0&0&0
\end{bmatrix} .
\]
We check with Sage:
sage: P*u1
sage: P*u2
sage: P*u3
Since its pivots are in the first, second, and last columns, we conclude that variables
\( y_1 , \ y_2, \ \mbox{and } \quad y_5 \) are
leading (or specific) variables, and
\( y_3 ,\ y_4 \) are free variables. We set free variables to be in turn 1 and 0 to obtain the two systems of equations
■
Oblique projections are defined by their range and null space. A formula for the matrix representing the projection
with a given range and null space can be found as follows. Let the vectors
\( {\bf u}_1 , \ldots {\bf u}_n \)
form a basis for the range of the projection, and assemble these vectors in the
m-by-
n matrix
A.
The range and the null space are complementary spaces, so the null space has dimension
m - n. It follows
that the orthogonal complement of the null space has dimension
n. Let
\( {\bf v}_1 , \ldots {\bf v}_n \) form a basis for the orthogonal complement of the
null space of the projection, and assemble these vectors in the matrix
B. Then the projection is
defined by
\[
{\bf P} = {\bf A} \left( {\bf B}^{\mathrm T} {\bf A} \right)^{-1} {\bf B}^{\mathrm T} .
\]
This expression generalizes the formula for orthogonal projections given above.
Gramm-Schmidt
In many applications, problems could be significantly simplified by choosing an appropriate basis in which vectors are orthogonal to one another.
The Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space
\( \mathbb{R}^n \) equipped with the standard inner product. The Gram–Schmidt process takes a finite, linearly independent set
\( S = \{ {\bf u}_1 , \ldots , {\bf u}_k \} \) for \( k \le n \)
and generates an orthogonal set \( S' = \{ {\bf v}_1 , \ldots , {\bf v}_k \} \) that spans the same k-dimensional subspace of
\( \mathbb{R}^n \) as S.
The method is named after a Danish actuary Jørgen Pedersen Gram (1850-1916) and a German mathematician Erhard Schmidt (1875-1959) but it appeared earlier in the work of Laplace and Cauchy.
The complexity of the Gram--Schmidt algorithm is \( 2mn^2 \) flops (floating point arithmetic operations).
Before presenting the Gram--Schmidt process, we recall the projection of the vector v on u:
\[
\mbox{proj}_{\bf u} ({\bf v}) = \frac{\langle {\bf v} , {\bf u} \rangle}{\langle {\bf u} , {\bf u} \rangle}\,{\bf u} = \frac{\langle {\bf v} , {\bf u} \rangle}{\| {\bf u} \|^2} \,{\bf u} ,
\]
where \( \langle {\bf v} , {\bf u} \rangle \) denotes the inner product of the vectors v and u.
This operator projects the vector v orthogonally onto the line spanned by vector u.
Gram--Schmidt process converts a basis
\( S = \{ {\bf u}_1 , \ldots , {\bf u}_k \} \) into an orthogonal basis \( S' = \{ {\bf v}_1 , \ldots , {\bf v}_k \} \) by performing the following steps:
\begin{align*}
{\bf v}_1 &= {\bf u}_1 ,
\\
{\bf v}_2 &= {\bf u}_2 - \frac{\langle {\bf v}_1 , {\bf u}_2 \rangle}{\| {\bf v}_1 \|^2} \, {\bf v}_1 = {\bf u}_2 - \mbox{proj}_{{\bf v}_1} ({\bf u}_2 ,
\\
{\bf v}_3 &= {\bf u}_3 - \frac{\langle {\bf v}_1 , {\bf u}_3 \rangle}{\| {\bf v}_1 \|^2} \, {\bf v}_1 - \frac{\langle {\bf v}_2 , {\bf u}_3 \rangle}{\| {\bf v}_2 \|^2} \, {\bf v}_2 = {\bf u}_3 - \mbox{proj}_{{\bf v}_1} ({\bf u}_3 ) - \mbox{proj}_{{\bf v}_2} ({\bf u}_3 ) ,
\\
\vdots & \quad \vdots
\\
{\bf v}_k &= {\bf u}_k - \sum_{j=1}^{k-1} \mbox{proj}_{{\bf v}_j} ({\bf u}_k) .
\end{align*}
To convert the orthogonal basis into an orthonormal basis
\( \{ {\bf q}_1 = {\bf v}_1 / \| {\bf v}_1 \| , \ldots , {\bf q}_k = {\bf v}_k / \| {\bf v}_k \| , \)
normalize the orthogonal basis vectors.
Example.
Assume that the vector space \( \mathbb{R}^3 \) has the Euclidean inner product. Apply the Gram-Schmidt process to transform the basis vectors
\[
{\bf u}_1 = \left[ 2, 1, 1 \right]^{\mathrm T} , \quad {\bf u}_2 = \left[ 1, 2, 1 \right]^{\mathrm T} , \quad {\bf u}_3 = \left[ 1, 1, 2 \right]^{\mathrm T}
\]
into an orthogonal basis \( \{ {\bf v}_1 , {\bf v}_2 , {\bf v}_3 \} , \) and then normalize the orthogonal basis vectors to obtain an orthonormal basis
\( \{ {\bf q}_1 , {\bf q}_2 , {\bf q}_3 \} . \)
Solution.
Step 1: \( {\bf v}_1 = {\bf u}_1 = \left[ 2, 1, 1 \right]^{\mathrm T} , \) with
\( \| {\bf v}_1 \| = \| \left[ 2, 1, 1 \right] \| = \sqrt{6} . \)
Step 2: Vector \( {\bf v}_2 = {\bf u}_2 - \frac{\langle {\bf v}_1 , {\bf u}_2 \rangle}{\| {\bf v}_1 \|^2} \, {\bf v}_1 = {\bf u}_2 - \frac{5}{6}\,{\bf u}_1 =
\frac{1}{6} \left[ -4, 7, 1 \right]^{\mathrm T} . \) We can drop factor 1/6 and consider vector \( {\bf v}_2 = \left[ -4, 7, 1 \right]^{\mathrm T} . \)
Step 3: \( {\bf v}_3 = {\bf u}_3 - \frac{\langle {\bf v}_1 , {\bf u}_3 \rangle}{\| {\bf v}_1 \|^2} \, {\bf v}_1 -
\frac{\langle {\bf v}_2 , {\bf u}_3 \rangle}{\| {\bf v}_2 \|^2} \, {\bf v}_2 = \frac{4}{11} \left[ -1, -1, 3 \right]^{\mathrm T} . \)
We can drop factor 4/11 and set \( {\bf v}_3 = \left[ -1, -1, 3 \right]^{\mathrm T} . \)
Step 4: Normalization: \( {\bf q}_1 = \frac{{\bf v}_1}{ \| {\bf v}_1 \|} = \frac{1}{\sqrt{6}} \left[ 2, 1, 1 \right]^{\mathrm T} , \)
\( {\bf q}_2 = \frac{{\bf v}_2}{ \| {\bf v}_2 \|} = \frac{1}{\sqrt{66}} \left[ -4, 7, 1 \right]^{\mathrm T} , \) and
\( {\bf q}_3 = \frac{{\bf v}_3}{ \| {\bf v}_3 \|} = \frac{1}{\sqrt{11}} \left[ -1, -1, 3 \right]^{\mathrm T} . \)
■
Example. Let \( L\,:\, \mathbb{R}^3 \, \mapsto \, \mathbb{R}^3 \) be the
orthogonal projection onto the plane \( W: \, 4x-y +8z =0 . \) Then
\( {\bf n} = \left[ 4, -1, 8 \right]^{\mathrm T} \) be the normal vector to the plane W.
For every vector z spanned on n, \( {\bf z} \in W^{\perp} . \)
Hence, \( L({\bf z}) = {\bf 0}, \) since ker(L) = \( W^{\perp} . \)
Now every vector in the plane W is mapped to itself by L. In fact, W equals the eigenspace
\( E_1 \) corresponding to the double eigenvalue \( \lambda_1 =1 . \)
Thus, finding a basis for W will give us a basis for \( E_1 . \) Let
\( {\bf u}_1 = \left[ 1, 4, 0 \right]^{\mathrm T} \) and
\( {\bf u}_2 = \left[ 2, 0, 1 \right]^{\mathrm T} \)
be two linearly independent vectors in W. They are not orthogonal, so we use Gram--Schmidt procedure to obtain
two orthogonal vectors in W:
\( {\bf v}_1 = \left[ 1, 4, 0 \right]^{\mathrm T} \) and
\( {\bf v}_2 = \left[ 32, -8, -17 \right]^{\mathrm T} \) that form a basis in W.
The projection operator/matrix onto W should have one double (not defective) eigenvalue
\( \lambda_1 =1 \) with eigenspace spanned on \( {\bf v}_1 \) and
\( {\bf v}_2 \) and one simple eigenvalue \( \lambda_2 =0 \) with
eigenspace spanned on the normal vector n. Since these three vectors form a basis for
\( \mathbb{R}^3 , \) we build a transition matrix from these eigenvectors:
\[
{\bf S} = \begin{bmatrix} 1&32&4 \\ 4&-8&-1 \\ 0&-17&8 \end{bmatrix} \quad \mbox{with} \quad
{\bf S}^{-1} = \frac{1}{1377} \begin{bmatrix} 81&324&0 \\ 32&-8&-17 \\ 324&-17& 136 \end{bmatrix} .
\]
Let
\( {\bf \Lambda} = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&0 \end{bmatrix} \) be the
diagonal matrix of eigenvalues of the projection operator
L, then its orthogonal projection matrix becomes
\[
{\bf P} = {\bf S} \, {\bf \Lambda} \, {\bf S}^{-1} = \frac{1}{81} \begin{bmatrix} 65&4&-32 \\ 4&80&8 \\ -32&8&17 \end{bmatrix} .
\]
We ask Sage to prove that
P is a projection matrix, which requires verification that it is idempotent and has eigenvalues 1,1,0:
Finally, we build the orthogonal reflection through the plane
W. We have all ingredients to find this matrix: the transition matrix S and its inverse.
The only difference reflection has compaired to projection on
W is that a vector
v orthogonal to the plane
will be mapped into its opposite but not into
0. Therefore, the orthogonal reflection matrix will have eigenvalues
1,1, and -1, and the diagonal matrix of eigenvalues will be
\( {\bf \Lambda} = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&-1 \end{bmatrix} . \)
This allows us to find the reflection matrix:
\[
{\bf Q} = {\bf S} \, {\bf \Lambda} \, {\bf S}^{-1} = \frac{1}{81} \begin{bmatrix} 49&8&-64 \\ 8&79&16 \\ -64&16&-47 \end{bmatrix} .
\]
Now we ask Sage to verify that
\( {\bf Q}^2 = {\bf I} , \) the identity matrix and that
\( {\bf Q}{\bf n} = -{\bf n} \) while
\( {\bf P}{\bf n} = {\bf 0} . \)
QR-decomposition
Suppose that
A is an
\( m \times n \) matrix with linearly independent
columns (full column rank), and
Q is the matrix that results by applying the Gram--Schmidt process
to the column vectors of
A. Then
A can be factored as
\[
{\bf A} = {\bf Q} \, {\bf R} = \left[ {\bf q}_1 \ {\bf q}_2 \ \cdots \ {\bf q}_n \right]
\begin{bmatrix} R_{1,1} & R_{1,2} & \cdots & R_{1,n} \\ 0& R_{2,2} & \cdots & R_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots & R_{n,n} \end{bmatrix} ,
\]
where
Q is an
\( m \times n \) matrix with orthonormal column vectors
(
\( \| {\bf q}_i \| =1, \quad \mbox{and} \quad {\bf q}^{\mathrm T}_i {\bf q}_j =0 \)
if
\( i \ne j \) ), and
R is an
\( n \times n \) invertible upper triangular matrix. This factorization is unique
if we require that the diagonal elements of
R be positive. If
\( R_{i,i} <0 , \)
we can switch the signs of
\( R_{i,i} , \ldots , R_{i,n} , \) and the vector
\( {\bf q}_{i} \)
to make the diagonal term
\( R_{i,i} \) positive.
In the above definition, \( {\bf Q}^{\mathrm T} {\bf Q} = {\bf I} ; \) If A is a square matrix,
then Q is orthogonal: \( {\bf Q}^{\mathrm T} {\bf Q} = {\bf Q} {\bf Q}^{\mathrm T} = {\bf I} . \)
If instead A is a complex square matrix, then there is a decomposition
\( {\bf Q}\, {\bf R} = {\bf A} , \) where Q is a unitary matrix
(so \( {\bf Q}^{\ast} {\bf Q} = {\bf I} \) ).
There are several methods for actually computing the QR decomposition, such as by means of the Gram--Schmidt process (
\( 2mn^2 \) flops, sensitive to rounding errors),
Householder transformations (\( 2mn^2 - (2/3) n^3 \) flops), or Givens rotations. Each has a number of advantages and disadvantages.
Example.
There is an example of QR decomposition:
\begin{align*}
{\bf A} &= \begin{bmatrix} -1&-1&1 \\ 1&3&3 \\ -1&-1&5 \\ 1&3&7 \end{bmatrix}
= \frac{1}{2} \begin{bmatrix} -1&1&-1 \\ 1&1&-1 \\ -1&1&1 \\ 1&1&1 \end{bmatrix}
\begin{bmatrix} 2&-4&2 \\ 0&2&8 \\ 0&0&4 \end{bmatrix}
\\
&= \left[ {\bf q}_1 \ {\bf q}_2 \ {\bf q}_3 \right] \begin{bmatrix} R_{1,1}&R_{1,2}&R_{1,3} \\ 0&R_{2,2}&R_{2,3} \\ 0&0&R_{3,3} \end{bmatrix} = {\bf Q}\, {\bf R} ,
\end{align*}
where column vectors
\( {\bf q}_1 , {\bf q}_2 , {\bf q}_3 \) are identified from the above
equation. ■
Recall that a matrix is full row rank when each of the rows of the matrix are linearly independent and full column rank
when each of the columns of the matrix are linearly independent.
Using QR decomposition for a full column rank matrix A, we can express its pseudo-inverse through matrices Q and R:
\begin{align*}
{\bf A}^{\dagger} &= \left( {\bf A}^{\mathrm T} {\bf A} \right)^{-1} {\bf A}^{\mathrm T} = \left( \left( {\bf Q}\,{\bf R} \right)^{\mathrm T} {\bf Q}\,{\bf R} \right)^{-1} \left( {\bf Q}\,{\bf R} \right)^{\mathrm T}
\\
&= \left( {\bf R}^{\mathrm T} {\bf Q}^{\mathrm T} {\bf Q} {\bf R} \right)^{-1} {\bf R}^{\mathrm T} {\bf Q}^{\mathrm T}
\\
&= \left( {\bf R}^{\mathrm T} {\bf R} \right)^{-1} {\bf R}^{\mathrm T} {\bf Q}^{\mathrm T} = {\bf R}^{-1} \left( {\bf R}^{\mathrm T} \right)^{-1} {\bf R}^{\mathrm T} {\bf Q}^{\mathrm T}
\\
&= {\bf R}^{-1} {\bf Q}^{\mathrm T} .
\end{align*}
For a square nonsingular A this is the inverse: \( {\bf A}^{-1} = \left( {\bf Q}\,{\bf R} \right)^{-1} = {\bf R}^{-1} {\bf Q}^{\mathrm T} . \)
Let us emphasize the main property of QR decomposition: Q
has the same range as A.
Spectral decomposition
One feature of Sage is that we can easily extend its capabilities by defining new
commands. Here will create a function that checks if an augmented matrix represents
a consistent system of equations. The syntax is just a bit complicated.
lambda
is the word that indicates we are making a new function, the input is temporarily
named A (think A ugmented), and the
name of the function is consistent. Everything
following the colon will be evaluated and reported back as the output.
sage: consistent = lambda A: not(A.ncols()-1 in A.pivots())
Execute this block above. There will not be any output, but now the
consistent
function will be defined and available. Now give it a try (after making sure to have
run the code above that defines
aug). Note that the output of
consistent() will be either
True
or
False.
sage: consistent(aug)
False
The consistent()
command works by simply checking to see if the last column
of
A is not
in the list of pivots. We can now test many different augmented matrices,
such as perhaps changing the vector of constants while keeping the
coefficient matrix fixed. Again, make sure you execute the code above
that defines coeff and const.
sage: consistent(coeff.augment(const))
False
sage: w = vector(QQ, [3,1,2])
sage: consistent(coeff.augment(w))
True
sage: u = vector(QQ, [1,3,1])
sage: consistent(coeff.augment(u))
False
Why do some vectors of constants lead to a consistent system with this
coefficient matrix, while others do not ? This is a fundamental question, which we will come to
understand in several different ways.
Least Square Approximation
The scientific custom of taking multiple observations of the same quantity and then selecting a single estimate
that best represents it has its origin the early part of the 16th century. At the beginning of the 19th century, two
of the foremost mathematicians of the time, the German C.F. Gauss (1777--1855) and the Frenchman A.M. Legendre (1752--1833),
proposed, idependently of each other, an optimality criterion that bears the same relation to the average.
The context for Legendre's proposal of the least squares was that of geodesy. At that time, France's scientists had
decided to adopt a new measurement system and proposed to use a unit length to be a meter, which would be equal
1/40,000,000 of the circumference of the earth. This necessitated an accurate determinantion of the said circumference
that, in turn, depended on the exact shape of the earth.
The credibility of the method of least squares were greatly enhanced by the Ceres incident. On January 1, 1801 the
Italian astronomer Giuseppe Piazzi sighted a heavently body that he strongly suspected to be a new planet. He announced
his discovery and named it Ceres. Unfortunately, 6 weeks later, before enough observations had been taken to make
possible accurate determinantion of its orbit, so as to ascertain that it was indeed a planet, Ceres disappared
behind the sun and was not expected to reemerge for nearly a year. Interest in this possibly new planet was widespread,
and the young Gauss proposed that an area of the sky be searched that was quite different from those suggested by
other astronomers; he turned out to be right! He became a celebrity upon his discovery, which includes two mathematical methods:
the row echelon reduction and the least square method.
In science and business, we often need to predict the relationship between two given variables. In many cases, we
begin by performing an appropriate experiments or statistical analyisis to obtain the necessary data. However, even
if a simple law governs the behavior of the variables, this law may not be easy to find because of errors introduced
in measuring or sampling. In practice, therefore, we are often content with a functional equation that provides a
close approximation. There are know three general techniques for finding functions which are closest to a given curve:
- linear regression using linear polynomials (matching straight lines);
- general linear regression (polynomials, etc.), and
- transformations to linear regression (for matching exponential or logarithmic functions).
Historically, besides to curve fitting, the least square technique is proved to be very useful in
statistical modeling of noisy data, and in geodetic modeling. We discuss three standard ways to solve teh least
square problem: the normal equations, the QR factorization, and the singular value decomposition.
Consider a typical application of least squares in curve fitting. Suppose that we are given a set of points
\( (x_i , y_i ) \) for
\( i = 0, 1, 2, \ldots , n, \) for which we may not be able (or may not want) to find a
function that passes through all points, but rather, we may want to find a function of a particular form that
passes as closely as possible to the points. For example,
suppose we’re given a collection of data points
(x,y):
\[
(1,1) , \quad (2,2), \quad (3,2)
\]
and we want to find the closest line
\( y = mx+b \) to that collection. If the line
went through all three points, we’d have:
\[
\begin{split}
m+b &=1 , \\
2m+b &=2, \\
3m+b &= 2, \end{split}
\]
which is equivalent to the vector equation:
\[
\begin{bmatrix} 1&1 \\ 1&2 \\ 1&3 \end{bmatrix} \begin{bmatrix} b \\ m \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 2 \end{bmatrix}
\qquad\mbox{or, in vector form:} \qquad {\bf A} \, {\bf x} = {\bf b} .
\]
In our example the line does not go through all three points, so this equation is not solvable.
Now we formulate the least square problem. Suppose that we have a set (usually linearly indepndent, but not necessarily)
of vectors \( \{ {\bf a}_1 , {\bf a}_2 , \ldots , {\bf a}_n \} \) and a given vector b.
We seek coefficients \( x_1 , x_2 , \ldots , x_n \) that produce a minimal error
\[
\left\| {\bf b} - \sum_{i=1}^n x_i \,{\bf a}_i \right\| .
\]
with respect to the Euclidean inner product on
\( \mathbb{R}^n . \) As long as we are interested only in linear combinations of a finite set
\( \{ {\bf a}_1 , {\bf a}_2 , \ldots , {\bf a}_n \} ,\) it is possible to transform the problem into one involving finite columns of numbers.
In this case, define a matrix
A with columns given by the linearly independent column vectors
\( {\bf a}_i , \)
and a vector
x whose entries are the unknown coefficients
xi. Then matrix
A has dimensions
m by
n, meaning that
\( {\bf a}_i \)
are vectors of length
m. The problem then can be reformulated by choosing
x that minimizing
\( \| {\bf A} {\bf x} - {\bf b} \|_2 \) because
\( {\bf A} {\bf x} = {\bf b} \) is an inconsistent linear system
of
m equations in
n unknowns. We call such a vector,
if it exists, a
least squares solution \( {\bf A} \hat{\bf x} = {\bf b} , \) and call
\( {\bf b} - {\bf A} \hat{\bf x} \) the least squares error vector.
If column vectors \( \{ {\bf a}_1 , {\bf a}_2 , \ldots , {\bf a}_n \} \) are linearly independent
(which will be assumed),
matrix A becomes full column rank. The vector \( \hat{\bf x} = x_1 {\bf a}_1 + x_2 {\bf a}_2 + \cdots + x_n {\bf a}_n \)
that is closest to a given vector b is its orthogonal projection onto the subspace spanned by the a's.
The hat over \( \hat{\bf x} \) indicates the best choice (in the sense that it minimizes
\( \| {\bf A} {\bf x} - {\bf b} \|_2 \) ) that gives the closest vector in the column space.
Therefore, to solve the least square problem is equivalent to find the orthogonal projection matrix P
on the column space such that \( {\bf P} {\bf b} = {\bf A}\,\hat{\bf x} . \)
The vector \( \hat{\bf x} \) is a solution to the least squares problem when
the error vector \( {\bf e} = {\bf b} - {\bf A} \hat{\bf x} \)
is perpendicular to the subspace. Therefore, this error vector makes right angle with all the vectors
\( \{ {\bf a}_1 , {\bf a}_2 , \ldots , {\bf a}_n \} . \) That gives the n equations
we need to find \( \hat{\bf x} : \)
\[
\begin{array}{c}
{\bf a}^{\mathrm T}_1 \left( {\bf b} - {\bf A} \hat{\bf x} \right) =0 \\
\vdots \quad \vdots \\
{\bf a}^{\mathrm T}_n \left( {\bf b} - {\bf A} \hat{\bf x} \right) =0
\end{array} \qquad \mbox{or} \qquad
\begin{bmatrix}
--- \, {\bf a}^{\mathrm T}_1 \, --- \\
\vdots \\
--- \, {\bf a}^{\mathrm T}_n \, ---
\end{bmatrix} \begin{bmatrix}
\quad \\
{\bf b} - {\bf A} \hat{\bf x} \\
\quad
\end{bmatrix} = \begin{bmatrix}
0 \\ \vdots \\ 0
\end{bmatrix} .
\]
The matrix in the right equation is
\( {\bf A}^{\mathrm T} . \) The
n equations are exactly
\[
{\bf A}^{\mathrm T} {\bf A} \, \hat{\bf x} = {\bf A}^{\mathrm T} \, {\bf b} .
\]
This equation is called the
normal equation.
Theorem: If W is a finite-dimensional subspace of an inner product vector space
V, and if b is a vector in V, then \( \mbox{proj}_W ({\bf b}) \)
is the best approximation to b from W in the sense that
\[
\| {\bf b} - \mbox{proj}_W {\bf b} \| < \| {\bf b} - {\bf w} \|
\]
for every vector
w in
W that is different from
\( \mbox{proj}_W ({\bf b}) . \) ■
To solve the normal equation, we need one more definition: for an arbitrary \( m \times n \) matrix A,
its pseudoinverse is defined as an \( n \times m \) matrix, denoted by
\( {\bf A}^{\dagger} , \) that satisfies all four criteria:
- \( {\bf A}\,{\bf A}^{\dagger} \,{\bf A} = {\bf A}; \)
- \( {\bf A}^{\dagger} {\bf A} \,{\bf A}^{\dagger} = {\bf A}^{\dagger} ; \)
- \( \left( {\bf A} \,{\bf A}^{\dagger} \right)^{\ast} = {\bf A} \,{\bf A}^{\dagger} \)
(so \( {\bf P} = {\bf A} \,{\bf A}^{\dagger} \) is self-adjoint m-by-m matrix) ;
- \( \left( {\bf A}^{\dagger} {\bf A} \right)^{\ast} = {\bf A}^{\dagger} {\bf A} \)
(so \( {\bf Q} = {\bf A}^{\dagger}{\bf A} \) is self-adjoint n-by-n matrix). ■
A pseudoinverse exists for arbitrary matrix A, but when the latter has full rank,
\( {\bf A}^{\dagger} \) can be expressed as a simple algebraic formula.
In particular, when A has linearly independent columns (and thus matrix \( {\bf A}^{\ast} \,{\bf A} \)
is invertible), \( {\bf A}^{\dagger} \) can be computed as:
\[
{\bf A}^{\dagger} = \left( {\bf A}^{\ast} {\bf A} \right)^{-1} {\bf A}^{\ast} .
\]
This particular pseudoinverse constitutes a left inverse, since, in this case,
\( {\bf A}^{\dagger} {\bf A} = {\bf I}_n . \)
When
A has linearly independent rows (matrix
\( {\bf A}\,{\bf A}^{\ast} \)
is invertible),
\( {\bf A}^{\dagger} \) can be computed as:
\[
{\bf A}^{\dagger} = {\bf A}^{\ast} \left( {\bf A}^{\ast} {\bf A} \right)^{-1} .
\]
This is a right inverse, as
\( {\bf A} {\bf A}^{\dagger} = {\bf I}_m . \) ■
The symmestric matrix \( {\bf A}^{\ast} {\bf A} \) is n by n. It is
invertible if the a's (column vectors) are independent. For a full column rank m-by-n real matrix A, the solution of least squares problem
becomes \( \hat{\bf x} = \left( {\bf A}^{\mathrm T} {\bf A} \right)^{-1} {\bf A}^{\mathrm T} \, {\bf b} . \)
The projection m-by-m matrix on the subspace of columns of A (range of m-by-n matrix A) is
\[
{\bf P} = {\bf A} \,\left( {\bf A}^{\mathrm T} {\bf A} \right)^{-1} {\bf A}^{\mathrm T} = {\bf A} \,{\bf A}^{\dagger} .
\]
Then
\[
{\bf A} \hat{\bf x} = {\bf A} \left( {\bf A}^{\mathrm T} {\bf A} \right)^{-1} {\bf A}^{\mathrm T} \, {\bf b} .
\]
So to solve the least square problem
\( {\bf A} {\bf x} = {\bf b} , \) which is inconsistent,
one can find the nearest solution
\( {\bf A} \hat{\bf x} = {\bf P}\,{\bf b} . \) ■
Theorem: Let A be an \( m \times n \) matrix and
\( {\bf A}^{\dagger} \) be its pseudoinverse n-by-m matrix.
- \( {\bf P} = {\bf A}\,{\bf A}^{\dagger} \) and \( {\bf Q} = {\bf A}^{\dagger} {\bf A} \)
are orthogonal projection operators (so they are idempotent \( {\bf P}^2 = {\bf P} , \quad {\bf Q}^2 = {\bf Q} \)
and self-adjoint \( {\bf P} = {\bf P}^{\ast} , \quad {\bf Q} = {\bf Q}^{\ast} \) );
- P is the orthogonal projector onto the range of A (which equals the
orthogonal complement of the kernel of \( {\bf A}^{\ast} \) );
- Q is the orthogonal projector onto the range of \( {\bf A}^{\ast} \) (which equals the
orthogonal complement of the kernel of A);
- \( \left( {\bf I} - {\bf P} \right) \) is the orthogonal projector onto the kernel of
\( {\bf A}^{\ast} ; \)
- \( \left( {\bf I} - {\bf Q} \right) \) is the orthogonal projector onto the kernel of
A;
- ker ( \( {\bf A}^{\dagger} \) ) = ker ( \( {\bf A}^{\ast} \) );
- Range ( \( {\bf A}^{\dagger} \) ) = Range ( \( {\bf A}^{\ast} \) ). ■
Now we derive the normal equation using another approach: calculus.
To find the best approximation, we look for the x where the gradient of
\( \| {\bf A} {\bf x} = {\bf b} \|_2^2 = \left( {\bf A} {\bf x} = {\bf b} \right)^{\mathrm T} \left( {\bf A} {\bf x} = {\bf b} \right) \)
vanishes. So we want
\begin{align*}
0 &= \lim_{\epsilon \mapsto 0} \frac{\left( {\bf A} ({\bf x} + \epsilon ) - {\bf b} \right)^{\mathrm T} \left( {\bf A} ({\bf x} + \epsilon ) - {\bf b} \right) - \left( {\bf A} {\bf x} - {\bf b} \right)^{\mathrm T} \left( {\bf A} {\bf x} - {\bf b} \right)}{\| \epsilon \|_2}
\\
&= \lim_{\epsilon \mapsto 0} \frac{2\epsilon^{\mathrm T} \left( {\bf A}^{\mathrm T} {\bf A} {\bf x} - {\bf A}^{\mathrm T} {\bf b} \right) + \epsilon^{\mathrm T} {\bf A}^{\mathrm T} {\bf A} \epsilon}{\| \epsilon \|_2} .
\end{align*}
The second term
\[
\frac{\left\vert \epsilon^{\mathrm T} {\bf A}^{\mathrm T} {\bf A} \epsilon \right\vert}{\| \epsilon \|_2} \le \frac{\| {\bf A} \|_2^2 \| \epsilon \|_2^2}{\| \epsilon \|_2} = \| {\bf A} \|_2^2 \| \epsilon \|_2 \, \mapsto \, 0
\]
approaches 0 as ε goes to 0, so the factor
\( {\bf A}^{\mathrm T} {\bf A} {\bf x} - {\bf A}^{\mathrm T} {\bf b} \)
in the first term must also be zero, or
\( {\bf A}^{\mathrm T} {\bf A} {\bf x} = {\bf A}^{\mathrm T} {\bf b} . \)
This is a system of
n linear equations in
n unknowns, the normal equation. ■
Why is \( \hat{\bf x} = \left( {\bf A}^{\mathrm T} {\bf A} \right)^{-1} {\bf A}^{\mathrm T} \, {\bf b} \)
the minimizer of \( \| {\bf A} {\bf x} - {\bf b} \|_2^2 ? \) We can note that the
Hessian \( {\bf A}^{\mathrm T} {\bf A} \) is positive definite, which means that the function is strictly
convex and any critical point is a global minimum.
Example. Let us find the least squares solution to the linear system
\[
\begin{split}
x_1 - x_2 &= 4 , \\
x_1 -2 x_2 &= 1, \\
-x_1 + 2x_2 &= 3 .
\end{split}
\]
It will be convenient to express the system in the matrix form
\( {\bf A} {\bf x} = {\bf b} , \) where
\[
{\bf A} = \begin{bmatrix} 1&-1 \\ 1&-2 \\-1&2 \end{bmatrix} , \qquad {\bf b} = \begin{bmatrix} 4\\ 1 \\ 3 \end{bmatrix} .
\]
It follows that
\begin{align*}
{\bf A}^{\mathrm T} {\bf A} &= \begin{bmatrix} 1&1&-1 \\ -1&-2&2 \end{bmatrix} \begin{bmatrix} 1&-1 \\ 1&-2 \\-1&2 \end{bmatrix} =
\begin{bmatrix} 3 & -5 \\ -5 & 9 \end{bmatrix} ,
\\
{\bf A} {\bf A}^{\mathrm T} &= \begin{bmatrix} 2&3&-3 \\ 3&5&-5 \\ -3&-5&5 \end{bmatrix} ,
\\
{\bf A}^{\mathrm T} {\bf b} &= \begin{bmatrix} 1&1&-1 \\ -1&-2&2 \end{bmatrix} \begin{bmatrix} 4\\ 1 \\ 3 \end{bmatrix} = \begin{bmatrix} 2 \\ 0 \end{bmatrix} ,
\end{align*}
so the normal system
\( {\bf A}^{\mathrm T} {\bf A} \, {\bf x} = {\bf A}^{\mathrm T} {\bf b} \) becomes
\[
\begin{bmatrix} 3 & -5 \\ -5 & 9 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 2 \\ 0 \end{bmatrix} .
\]
Solving this system yields a unique least squares solution, namely,
\[
x_1 = 9, \quad x_2 = 5.
\]
The least squares error vector is
\[
{\bf b} - {\bf A} {\bf x} = \begin{bmatrix} 4 \\ 1 \\ 3 \end{bmatrix} - \begin{bmatrix} 1&-1 \\ 1&-2 \\-1&2 \end{bmatrix}
\begin{bmatrix} 2 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \\ 2 \end{bmatrix}
\]
and the least squares error is
\( \left\| {\bf b} - {\bf A} {\bf x} \right\| = 2\sqrt{2} \approx 2.82843 . \)
The pseudoinverse is the following 2 by 3 matrix:
\[
{\bf A}^{\dagger} = \left( {\bf A}^{\mathrm T} {\bf A} \right)^{-1} {\bf A}^{\mathrm T} = \frac{1}{2} \begin{bmatrix} 4&-1&1 \\ 2&-1&1 \end{bmatrix} ,
\]
and the projectors on the range of
A and on the range of
\( {\bf A}^{\mathrm T} \) (which is the orthogonal complement of the kernel of
A) are
\[
{\bf P} = {\bf A} {\bf A}^{\dagger} = \frac{1}{2} \begin{bmatrix} 2&0&0 \\ 0&1&-1 \\ 0&-1&1 \end{bmatrix} \quad\mbox{and} \quad
{\bf Q} = {\bf A}^{\dagger} {\bf A} = \begin{bmatrix} 1&0 \\ 0& 1 \end{bmatrix} ,
\]
respectively.
Example.
Find the least square solutions, the least squares error vector, and the least squares error of the linear system
\[
\begin{split}
3x_1 + 2x_2 + x_3 &= 2 , \\
-x_1 + x_2 + 4x_3 &= -2, \\
x_1 + 4x_2 + 9 x_3 &= 1 .
\end{split}
\]
The matrix form of the system is
\( {\bf A} {\bf x} = {\bf b} , \) where
\[
{\bf A} = \begin{bmatrix} 3&2&1 \\ -1&1&4 \\ 1&4&9 \end{bmatrix} \qquad\mbox{and} \qquad {\bf b} = \begin{bmatrix} 2 \\ -2 \\ 1 \end{bmatrix} .
\]
Since the matrix
A is singular and the rank of the augmented matrix
\( \left[ {\bf A} \, | \, {\bf b} \right] \)
is 3, the given system of algebraic equations is inconsistent. It follows that
\[
{\bf A}^{\mathrm T} {\bf A} = \begin{bmatrix} 11&9&8 \\ 9&21&42 \\ 8&42&98 \end{bmatrix} \qquad\mbox{and} \qquad {\bf A}^{\mathrm T} {\bf b} = \begin{bmatrix} 9 \\ 6 \\ 3 \end{bmatrix} ,
\]
so the augmented matrix for the normal system
\( {\bf A}^{\mathrm T} {\bf A} {\bf x} = {\bf A}^{\mathrm T} {\bf b} \) is
\[
\left[
\begin{array}{ccc|c} 11&9&8&9 \\ 9&21&42&6 \\ 8&42&98&3
\end{array} \right] .
\]
The reduced row echelon form of this matrix is
\[
\left[
\begin{array}{ccc|c} 1&0&- \frac{7}{5}&\frac{9}{10} \\ 0&1&\frac{13}{5}&-\frac{1}{10} \\ 0&0&0&0
\end{array} \right]
\]
from which it follows that there are infinitely many least square solutions, and they are given by the parametric eqwuations
\[
\begin{split}
x_1 &= \frac{7}{5}\, t + \frac{9}{10} \\
x_2 &= - \frac{13}{5}\, t - \frac{1}{10} , \\
x_3 &= t . \end{split}
\]
As a check, let us verify that all least squares solutions produce the same least squares error vector and the same least squares error.
To see this so, we first compute
\[
{\bf b} - {\bf A} \hat{\bf x} = \begin{bmatrix} 2 \\ -2 \\ 1 \end{bmatrix} - \begin{bmatrix} 3&2&1 \\ -1&1&4 \\ 1&4&9 \end{bmatrix}
\begin{bmatrix} \frac{7}{5}\, t + \frac{9}{10} \\ - \frac{13}{5}\, t - \frac{1}{10} \\ t \end{bmatrix} = \frac{1}{2} \begin{bmatrix} -1 \\ -2 \\ 1 \end{bmatrix} .
\]
Since
\( {\bf b} - {\bf A} \hat{\bf x} \) does not depend on
t, all least squares solutions produce
the same error vector, namely,
\( \| {\bf b} - {\bf A} \hat{\bf x} \| = \sqrt{\frac{3}{2}} .\)
■
SVD factorization
One of the most fruitful ideas in the theory of matrices is that of matrix decomposition or canonical form. The theoretical
utility of matrix decompositions has long been appreciated. Of many useful decompositions, the singular value decomposition---that is,
the factorization of a
m-by-
n matrix
A into the product
\( {\bf U}\, {\bf \Sigma} \,{\bf V}^{\ast} \)
of a unitary (or orthogonal)
\( m \times m \) matrix
U, a
\( m \times n \) 'diagonal' matrix
\( {\bf \Sigma} \) and another unitary
\( n \times n \) matrix
\( {\bf V}^{\ast} \) ---has assumed a special role. There are several reasons. In the first place,
the fact that the decomposition is achieved by unitary matrices makes it an ideal vehicle for discussing the geometry
of
n-space. Second, it is stable; small pertubations in
A corresponds to small pertubabtions in
\( {\bf \Sigma} .\)
Third, the diagonality of
\( {\bf \Sigma} \) makes it easy to operate and solve equations.
It is an intriguing observation that most of the classical matrix decompositions predated the widespread use of
matrices. In 1873, the Italian mathematician Eugenio Beltrami (1835--1899) published a first paper on SVD, which was
followed by the work of Camille Jordan in 1874, whom we can consider as a codiscover. Later James Joseph Sylvester (1814--1897),
Edhard Schmidt (1876--1959), and Hermann Weyl (1885--1955) were responsible for establishing the existence of the
singular value decomposition (SVD) and developing its theory. The term ``singular value'' seems to have come from the literature on integral equations.
The British-born mathematician Harry Bateman (1882--1946) used it in a research paper published in 1908.
Let
A be an arbitrary real-valued
\( m \times n \) matrix. Then
- \( {\bf A}^T {\bf A} \) and \( {\bf A} \, {\bf A}^T \) are
both symmetric positive semidefinite matrices of dimensions \( n \times n \) and \( m \times m ,\) respectively.
- The equality \( {\bf A} = {\bf U}\,{\bf S}\, {\bf V}^T \) is called the singular value decomposition (or SVD) of
A, where V is orthogonal \( n \times n \) matrix, U
is orthogonal \( m \times m \) matrix, and \( {\bf S} = {\bf U}^T\,{\bf A}\, {\bf V} \)
is diagonal with \( {\bf S} = \mbox{diag}( \sigma_1 , \sigma_2 , \ldots , \sigma_p ) , \) where
\( p = \min (m,n) \) and the nonnegative numbers \( \sigma_1 \ge \sigma_2 \ge \cdots \ge\sigma_p ) \ge 0 \) are
singular values of A.
- If r is rank of A, then A has exactly r positive singular values
\( \sigma_1 \ge \sigma_2 \ge \cdots \ge\sigma_r ) > 0 \) with \( \sigma_{r+1} = \sigma_{r+2} = \cdots = \sigma_p =0 . \)
Example. Consider the matrix
\[
{\bf A} = \begin{bmatrix} 1&-1 \\ 1&-2 \\-1&2 \end{bmatrix}
\]
that we met previously. Two symmetric matrices
\[
{\bf A}^T {\bf A} = \begin{bmatrix} 3&-5 \\ -5&9 \end{bmatrix} \quad \mbox{and} \quad
{\bf A} \, {\bf A}^T = \begin{bmatrix} 2&3&-3 \\ 3&5&-5 \\ -3&-5&5 \end{bmatrix} ,
\]
which is a singular one, share the same eigenvalues
\( \lambda_{1} = 6+ \sqrt{34} \approx 11.831, \quad \lambda_2 = 6 -\sqrt{34} \approx 0.169048, \)
having corresponding eigenvectors:
\[
{\bf u}_1 = \begin{bmatrix} 3- \sqrt{34} \\ 5 \end{bmatrix} , \quad {\bf u}_2 = \begin{bmatrix} 3+ \sqrt{34} \\ 5 \end{bmatrix} ,
\]
and, including
\( \lambda_{3} = 0 , \)
\[
{\bf v}_1 = \begin{bmatrix} 4- \sqrt{34} \\ -3 \\ 3 \end{bmatrix} , \quad {\bf v}_2 = \begin{bmatrix} 4+ \sqrt{34} \\ -3 \\ 3 \end{bmatrix} ,
\quad {\bf v}_3 = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} .
\]
Since these two matrices are symmetric, the corresponding eigenvectors are orthogonal. We can normalize these vectors
by dividing by
\( \| {\bf u}_1 \|_2 = \sqrt{68 - 6 \sqrt{34}} \approx 5.74581, \) \( \| {\bf u}_2 \|_2 = \sqrt{68 + 6 \sqrt{34}} \approx 10.1482 \)
and
\( \| {\bf v}_1 \|_2 = 2\sqrt{17 - 2 \sqrt{34}} \approx 4.62086, \)
\( \| {\bf v}_2 \|_2 = 2\sqrt{17 + 2 \sqrt{34}} \approx 10.7974 , \)
\( \| {\bf v}_3 \|_2 = \sqrt{2} \approx 1.41421 . \) Taking square roots of their
positive eigenvalues, we obtain singular values for matrix
A:
\[
\sigma_1 = \sqrt{6+ \sqrt{34}} \approx 3.43962 , \quad \sigma_2 = \sqrt{6- \sqrt{34}} \approx 0.411155 .
\]
Then we build two orthogonal matrices:
\[
{\bf U} = \left[ {\bf u}_1 , \ {\bf u}_2 \right] = \begin{bmatrix} \frac{3- \sqrt{34}}{\sqrt{68 -6\sqrt{34}}} & \frac{3+\sqrt{34}}{\sqrt{68 +6\sqrt{34}}} \\
\frac{5}{\sqrt{68 -6\sqrt{34}}} & \frac{5}{\sqrt{68 +6\sqrt{34}}} \end{bmatrix}
\]
and
\[
{\bf v} = \left[ {\bf v}_1 , \ {\bf v}_2 , \ {\bf v}_3 \right] = \begin{bmatrix} \frac{4- \sqrt{34}}{2\sqrt{17 -2\sqrt{34}}} & -\frac{3}{2\sqrt{17 +2\sqrt{34}}} & 0 \\
-\frac{3}{2\sqrt{17 -2\sqrt{34}}} & -\frac{3}{2\sqrt{17 +2\sqrt{34}}} & \frac{1}{\sqrt{2}} \\
\frac{3}{2\sqrt{17 -2\sqrt{34}}} & \frac{3}{2\sqrt{17 +2\sqrt{34}}} & \frac{1}{\sqrt{2}} \end{bmatrix} ,
\]
and the 'diagonal' matrix
\[
{\bf \Sigma} = \begin{bmatrix} \sigma_1 &0&0 \\ 0&\sigma_2 & 0 \end{bmatrix} .
\]
Example.
Example.
To view this, type show(P+Q+R).
Numerical Methods
The condition number of an invertible matrix
A is defined to be
\[
\kappa ({\bf A}) = \| {\bf A} \| \, \| {\bf A}^{-1} \| .
\]
This quantity is always bigger than (or equal to) 1.
We must use the same norm twice on the right-hand side of the above equation. Sometimes the
notation is adjusted to make it clear which norm is being used, for example if we use the infinity
norm we might write
\[
\kappa_{\infty} ({\bf A}) = \| {\bf A} \|_{\infty} \, \| {\bf A}^{-1} \|_{\infty} .
\]
Inequalities
Regarding
Applications
- into \(N\)
subintervals,
- the approximation given by the Riemann sum approximation.
sage: f1(x) = x^2
sage: f2(x) = 5-x^2
sage: f = Piecewise([[(0,1),f1],[(1,2),f2]])
sage: f.trapezoid(4)
Piecewise defined function with 4 parts, [[(0, 1/2), 1/2*x],
[(1/2, 1), 9/2*x - 2], [(1, 3/2), 1/2*x + 2],
[(3/2, 2), -7/2*x + 8]]
sage: f.riemann_sum_integral_approximation(6,mode="right")
19/6
sage: f.integral()
Piecewise defined function with 2 parts,
[[(0, 1), x |--> 1/3*x^3], [(1, 2), x |--> -1/3*x^3 + 5*x - 13/3]]
sage: f.integral(definite=True)
3