Preface
This section of the tutorial gives an introduction to complex numbers. The emphasis is made on applications of Mathematica to handle basic operations with complex numbers but not to describe deep theory, which can be found in other resourses.
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Glossary
Complex numbers
Complex numbers were introduced by the Italian famous gambler and mathematician Gerolamo Cardano (1501--1576) in 1545 while he found the explicit formula for all three roots of a cube equation. Many mathematicians contributed to the full development of complex numbers. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli (baptized on 20 January 1526; died 1572). The notations 1 and i for unit vectors in the horizontal positive direction and the vertical positive direction, respectively, were introduced by Leonhard Euler (1707--1783) who visualized complex numbers as points with rectangular coordinates, but did not give a satisfactory foundation for complex number theory. He also suggested to drop the unit vector 1 in presenting vectors on the plane. It was Carl Friedrich Gauss (1777--1855) who introduced the term complex number. Cauchy, a French contemporary of Gauss, extended the concept of complex numbers to the notion of complex functions. University of Rhode Island professor Orlando Merino (born in 1954) has written an essay on history of discovery of complex numbers.
Complex numbers can be identified with three sets: points on the plane, denoted by ℝ², set of all (free) vectors on the plane, and the set of all ordered pairs of real numbers z = (x,y), where the first coordinate is denoted as ℜz = x (or Rez) and called for historical reasons real part of complex number z, and the second coordinate is denoted as ℑz = y (or Imz) and called the imaginary part of complex number z. A geometric plot of complex numbers as points z = x + jy using the x-axis as the real axis and y-axis as the imaginary axis is referred to as an Argand diagram. Such plots are named after Jean-Robert Argand (1768–1822) who introduced it in 1806, although they were first described by Norwegian–Danish land surveyor and mathematician Caspar Wessel (1745–1818).
The set of complex numbers ℂ is one of the above three sets equipped with arithmetic operations (addition, subtraction, multiplication, and division) that satisfy usual axioms of real numbers. While addition and subtraction are inherited from vector algebra, multiplication and division satisfy specific rules based on the identity j² = -1.
For a long time it was thought that complex numbers were just toys invented and played with only by mathematicians. After all, no single quantity in the real world can be measured by an imaginary number, a number that lives only in the imagination of mathematicians. However, in 1926, Erwin Schrödinger (1887--1961) discovered that in the language of the world of the subatomic particles, complex numbers were the indispensable alphabet. Although no single measurable physical quantity corresponds to a complex number, a pair of physical quantities can be represented very naturally by a complex number. For instance, a wave, which always consists of an amplitude and a phase, begs a representation by a complex number.
Mathematica has three different characters to represent the imaginary unit: I and two others are also used in Wolfram language when entered into worksheet with commands \[ImaginaryI] or \[ImaginaryJ], provide outputs 𝕚 or 𝕛, respectively.
Since there is no universal notation for a unit vector in the vertical direction on the complex plane, Mathematica uses two of them: i and j. Euler suggested to use i (\( {\bf i}^2 =-1 \) ) , so mathematicians follow him; however, in engineering and computer science it is common to use j (\( {\bf j}^2 =-1 \) ) .
i -- a unit imaginary vector in Mathematics, denoted by \[ImaginaryI] in Wolfram language and is displayed as 𝕚.
j -- a unit imaginary vector in Engineering and Computer Science, denoted by \[ImaginaryJ] in Wolfram language and is displayed as 𝕛.
Complex -- convert a pair of reals to a complex number
Re -- real part of a complex number
Im -- imaginary part of a complex number
ReIm -- gives the list {Re[z], Im[z]}
Abs -- absolute value
Arg -- argument (phase angle in radians)
Conjugate -- complex conjugate
ComplexExpand -- expand symbolic expressions into real and imaginary parts
ExpToTrig, TrigToExp -- convert between complex exponentials and trigonometric functions
The "Cartesian" plane ℝ² is a plane whose points are labelled with ordered pairs: {x, y} of real numbers x and y, whereas the coordinates of the complex plane ℂ are complex number of the form (x + I y). The Wolfram Language provides easy connections between the coordinates of the two planes.
Complex allows only one input, you may want to extend it by introducing a special one:
Convert to polar form:
We can find all roots of a number using the following code:
Function[x, Function[y, ( Abs[y] ^ (1/x) *
( Cos[((Arg[y] + 360° * Range[0, x - 1]) / x)] +
I*Sin[((Arg[y] + 360° * Range[0, x - 1]) / x)]))
] ]
For instance, suppose we want to find all four roots of (-4)^(1/4) :
The following animation, developed by Wolfram Research, shows all n-th roots of unity \( \left( 1 \right)^{1/n} = \sqrt[n]{1} \) for different positive integer values of n: \( n=1,2,\ldots , 14 . \)
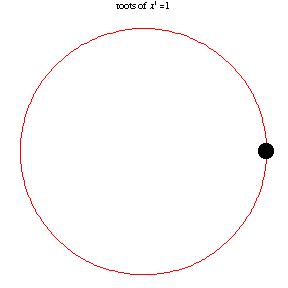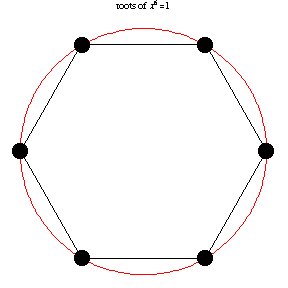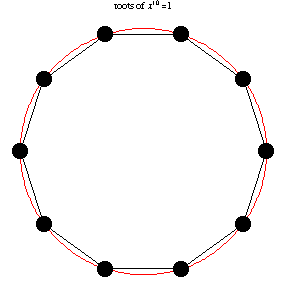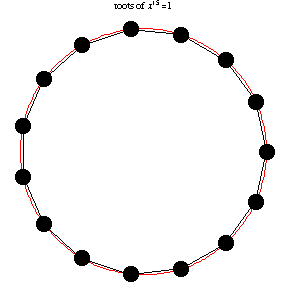 We present the following code to find and plot all roots on complex plane:
We present the following code to find and plot all roots on complex plane:
Module[{nSol, list}, nSol = NSolve[equation, variable];
list = {Re[x], Im[x]} /. nSol;
Return[ListPlot[list, PlotStyle -> PointSize[0.03], opts]];]

CPlot[Table[\[Omega]^k , { k, 0, n-1}]]];
ShowNRoots[9]
ParametricPlot3D[{r*Cos[theta], r*Sin[theta], r^(1/n) * Cos[theta/n]},
{r, 0, 2}, {theta, 0, 2*n*Pi},
PlotPoints -> {resolution, resolution*n},
Boxed -> False, Axes ->False, AspectRatio -> 1, ViewPoint -> {-3, -3, 0}]

ParametricPlot3D[{r*Cos[theta], r*Sin[theta], theta},
{r, 0, 2}, {theta, 0, 2*n*Pi},
PlotPoints -> {resolution, resolution*n},
Boxed -> False, Axes ->False, AspectRatio -> 1/2, ViewPoint -> {-3, -2, 3}]

Module[{r}, r = Map[{Re[#], Im[#]} &, z];
ListPlot[r, PlotStyle -> PointSize[0.1], AspectRatio ->1,
PlotRange -> {{-1.1, 1.1}, {-1.1, 1.1}},
PlotRegion -> {{0.05, 0.95}, {0.05, 0.95}}]]
CPlot[{1, omega, omega^2}]

To plot lists of complex number you may want to implement the following definition
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)