es

Linear Systems

Linear algebra is the study of linear sets of equations and their transformation properties. Linear algebra is central to almost all areas of mathematics.

A linear equation in the variables x₁, x₂, … , xn is an equation of the form

\[ a_1 x_1 + a_2 x_2 + \cdots + a_n x_n = b , \]
where b and the coefficients 𝑎1, 𝑎2, … , 𝑎n are given real or complex numbers. It is always assumed that not all coefficients are equal to zero. The subscript n can be any positive integer.

Observe that a linear equation does not involve products or roots of variable or any nonlinear function of these variables. All variables occur only to the first power and do not appear as their products.

Example 1: The following equations are linear:
\[ \begin{split} 2\,x - 3\, y &=1, \\ \cos (\pi )\,x + 5\,y &= 2, \end{split} \qquad\quad \begin{split} \sin (\pi )\,x^2 - \sqrt{\pi}\,y &= 8, \\ 7\,x - 2\,y &= 1. \end{split} \]

The following are not linear equations:
\[ \begin{split} 2\,x^2 - 3\, y &=1, \\ \cos (x) + x\,y &= 2, \end{split} \qquad\quad \begin{split} 4\,x - \sqrt{y} &= 8, \\ (x - 2y )^2 &= 1. \end{split} \]

End of Example 1
A system of linear equations (or, more briefly, a linear system) is a collection of one or more linear equations involving the same variables---say x₁, x₂, … , xn. The variables are called unknowns. Sometimes, a system of linear equations is called a set of simultaneous equations; such terminology emphasizes that a solution is an assignment of values to each of the unknowns.

Let us start with a system of two linear equations with two unknowns, such as

\[ \begin{cases} 2x + 3y &= 7, \\ 3x-5y &= 1 . \end{cases} \]
To solve this system, one would take a combination of the two equations and eliminate one of the variables. We can multiply the first equation by 3 and subtract two times the first, giving us
\[ 3 \left( 2x + 3y \right) - 2 \left( 3x--5y \right) = 3\cdot 7 - 2\cdot 1 = 19 , \]
which simplifies to
\[ 19y = 19 , \]
yielding the equivalent system
\[ \begin{cases} 2x + 3y &= 7, \\ \phantom{2x +}19y &= 19 . \end{cases} \]
Now we can solve the latter for y giving y = 1. Substituting this value into the first equation, we obtain
\[ \begin{cases} 2x &= 4, \\ \phantom{2x +}y &= 1 . \end{cases} \]
So the solution of the given system is x = 2 and y = 1. Let us calculate how many arithmetic operations were needed to obtain this answer. Equation 19 y = 19 obtained with 7 arithmetic operations (6 multiplications and 1 subtraction). Division is required to get y = 1. Then we substitute this value for y into the first equation (with 1 multiplication). Finally division by 2 gives us the value of x. So totally, we made 10 arithmetic operations (called flops).

However, we can save 3 multiplications on expense of 1 division if we multiply the first row by 3/2 (a computer does not afraid of using rational numbers). This yields 8 flops (arithmetic operations) to solve the given linear system.

Do you know another option to solve this system of linear equations? Most likely you were taught that substitution will work. Indeed, expressing x from the first equation (with 3 arithmetic operations: 1 subtraction and 2 divisions), we obtain

\[ x = \frac{7}{2} - \frac{3}{2}\,y . \]
Next we substitute this expression into the second equation (it requires 2 multiplications)
\[ 3 \cdot \left(\frac{7}{2} - \frac{3}{2}\,y \right) - 5\, y = 1 \qquad \iff \qquad \frac{21}{2} - \frac{9}{2}\, y - 5\, y = 1 . \]
Two arithmetic operations are required for simplification and one division provides the answer for y. Substituting back into expression for x and performing 2 arithmetic operation, we finally obtain the solution. Therefore, substitution procedure requires 9 arithmetic operations.

Another option to find the solution is to plot each equation and determine the intersection (if any). Python helps

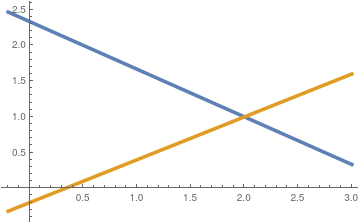
Since every linear equation in two unknowns x and y

\[ a\,x + b\,y = c , \]
where 𝑎 b and c are given constants, defines a straight line on the plane, we can visualize a system of linear equations
\[ \begin{cases} a_1 x + b_1 y &= c_1 , \\ a_2 x + b_2 y &= c_2 , \end{cases} \]
by plotting these two lines. Besides a unique solution as in the previous example, two lines can be parallel (no solution) or coincide (infinite many solutions). The following two equations illustrate these two situations.
\[ \begin{cases} 3\, x -2\, y &= 1 , \\ 3\, x -2\, y &= 2 , \end{cases} \qquad \begin{cases} 3\, x -2\, y &= 1 , \\ 6\, x -4\, y &= 2 . \end{cases} \]

No solution
      
Infinite many solutions

A linear equation in the variables x₁, x₂, … , xn is an equation of the form

\[ a_1 x_1 + a_2 x_2 + \cdots + a_n x_n = b , \]
where b and the coefficients 𝑎1, 𝑎2, … , 𝑎n are given real or complex numbers. It is always assumed that not all coefficients are equal to zero. The subscript n can be any positive integer.

Observe that a linear equation does not involve products or roots of variable or any nonlinear function of these variables. All variables occur only to the first power and do not appear as their products.

Example 2: Let us solve the linear system
\[ \begin{split} x + 3\,y &= 4, \\ 3\,x + 9\, y &= 12 . \end{split} \]
We can eliminate x from the second equation by adding −3 times the first equation to the second equation. This yields the simplified system
\[ \begin{split} x + 3\,y &= 4, \\ \phantom{x + 9y}0 &= 0 . \end{split} \]
The second equation does not impose any restrictions on x and y and hence can be omitted. Thus, the solutions of the given system are those values of x and y that satisfy the single equation
\[ x + 3\,y = 4 \qquad \Longrightarrow \qquad x = 4 - 3\,y . \]
End of Example 2

In general, we claim that a linear system of two equations with two unknowns either has a unique solution, or no solution, or infinitely many solutions.

Now we turn our attention to three linear equations in three unknowns:

\[ \begin{split} a_1 x + b_1 y + c_1 z &= d_1 , \\ a_2 x + b_2 y + c_2 z &= d_2 , \\ a_3 x + b_3 y + c_3 z &= d_3 , \end{split} \]

in which the graphs of the equations are planes. The solutions of the given system, if any, correspond to the points where all three planes intersect. So we plot eight possible cases.

We plot one plane using the equation
\[ a\,x + b\,y + c\,z = a\,x_0 + b\,y_0 + c\, z_0 , \]
that passes through the point (x0, y0, z0) and having normal vector (𝑎, b, c).

The following figure shows the case when all three places coicide; then we have infinite many solutions.

Next figure shows that there is no solution when two coincident planes parallel to the third; no common intersection.

This graph shows the case of no solution because three parallel planes have no common intersection.
     
No solution

Next figure shows that there is no solution when two parallel planes crosses the third; no common intersection.

Example 3: Consider the linear system of equations:
\[ \begin{split} \phantom{10\,y +}z &= 0, \\ 10\,y -z &= 10 , \\ -10\,y -z &= 10 . \end{split} \]

Next figure shows that there is no solution. If we substitute z = 0 (from the first equation) into two other equations, we see that they have no common intersection.

Example 4: Consider the linear system of equations:
\[ \begin{split} 2*x+3\,y -z &= 0, \\ -3*x+2\,y -z &= 1 , \\ 4*x -10\,y -z &= 2 . \end{split} \]

Next figure shows that there is a unique solution. You will learn shortly how Python can detect this conclusion in a blank of eye.

Example 5: Consider the linear system of equations:
\[ \begin{split} \phantom{10\,y +}z &= 0, \\ 10\,y -z &= 0 , \\ -10\,y -z &= 0 . \end{split} \]

Next figure shows that there are infinitely many solutions. If we substitute z = 0 (from the first equation) into two other equations, we see that they are equivalent.

Example 6: Consider the linear system of equations:
\[ \begin{split} \phantom{10\,y +}z &= 0, \\ 10\,y -z &= 0 , \\ 5\,y -z/2 &= 0 . \end{split} \]

We will develop a systematic way to do this for any number of equations with arbitrary number of unknowns (often denoted as x1, x2, x3, …) through the use of matrices and vectors.

A system of linear equations in the variables x1, x2, x3, …, xn is a finite set of m linear equations of the form
\begin{equation} \label{EqLinear.1} \begin{split} a_{1,1} x_1 + a_{1,2} x_2 + a_{1,3} x_3 + \cdots + a_{1,n} x_n &= b_1 , \\ a_{2,1} x_1 + a_{2,2} x_2 + a_{2,3} x_3 + \cdots + a_{2,n} x_n &= b_2 , \\ \vdots \qquad\qquad \vdots & \vdots \\ a_{m,1} x_1 + a_{m,2} x_2 + a_{m,3} x_3 + \cdots + a_{m,n} x_n &= b_m . \end{split} \end{equation}
A solution to the system of equations above is an ordered n-tuple of numbers s1, s2, s3, …, sn that is a solution to each of the equations in the system. The set of all possible solutions is called the solution set of the system \eqref{EqLinear.1}.
The double subscripting on the coefficients 𝑎i,j of the given coefficients gives their location in the system---the first subscript indicates the equation in which the coefficient occurs, and the second indicates which unknown it multiplies. Foe example, 𝑎2,3 is the second equation and multiplies x3.
A system of linear equations (1) is called consistent if it has at least one solution, and it said to be inconsistent if it has no solution.

A special and important class of systems of linear equations that always have at least one solution is the class of homogeneous equations. These are systems where every bi = 0,    i = 1, 2, … , m. One solution to such a system will always be when each variable is 0. This means for a system of two or three variables, the graph of each equation in a homogeneous system passes through the origin.

A system of linear equations (1) is called homogeneous (with accent on "ge") if all terms in right side of Eq.(1) are zeroes, bi = 0,    i = 1, 2, … , m. A system (1) is known as inhomogeneous or nonhomogeneous if at least one entry bi ≠ 0.

 

Matrix Notation

The essential information of a linear system of m equations in n unknowns can be recorded compactly in a standard rectangular array called a matrix.
For a given linear system (1), the matrix A = (𝑎ij), whose (i, j) entry is the coefficient 𝑎ij of the system (1) is called the coefficient matrix:
\[ {\bf A} =\left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right] \quad \mbox{or} \quad {\bf A} =\left( \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) . \]
A matrix A whose elements are the coefficients 𝑎ij of a set of simultaneous linear equations (1) to which the column-vector b of right-hand side constant terms of Eq.(1) is appended, is called the augmented matrix. We denote the augmented matrix as
\[ \left( {\bf A}\,\vert\,{\bf b} \right) = \left( \begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_m \end{array} \right) , \qquad {\bf b} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix} . \]
When write an augmented matrix, we will usually drop the vertical line separating the coefficient matrix from the input vector b.

Maxime Bôcher.
The first known use of augmented matrices appeared between 200 B.C. and 100 B.C. in a Chinese manuscript entitled Nine Chapters of Mathematical Art. In this work, the coefficients were arranged in columns rather than in rows, as today in the majority of engineering, mathematical, and physical printings. However, the systems were successfully solved by performing operations on the columns. The actual use of the term augmented matrix appears to have been introduced by the American mathematician Maxime Bôcher (1867--1918) in his book Introduction to Higher Algebra, published in 1907. In addition to being an outstanding research mathematician and an expert in Latin, chemistry, philosophy, zoology, geography, meteorology, art, and music, Maxime Bôcher was an excellent expositor of mathematics whose elementary textbooks were greatly appreciated students and are still in demand today.

Example 7: Let us consider the linear system
\[ \begin{split} 2\,x + 3\,y + 4\, z &= 5, \\ 3\,x - 7\,y + 3\,z &= 2, \\ 4\,x + 5\,y - 8\,z &= 3. \end{split} \]
The coefficient matrix and the right side vector are
\[ {\bf A} = \begin{bmatrix} 2 & \phantom{-}3 & \phantom{-}4 \\ 3 & -7 & \phantom{-}3 \\ 4 & \phantom{-}5 & -8 \end{bmatrix} , \qquad {\bf b} = \begin{pmatrix} 5 \\ 2 \\ 3 \end{pmatrix} . \]
With this in hand, we build the corresponding augmented matrix:
\[ \left( {\bf A}\,|\,{\bf b} \right) = \left( \begin{array}{ccc|c} 2 & \phantom{-}3 & \phantom{-}4 & 5 \\ 3 & -7 & \phantom{-}3 & 2 \\ 4 & \phantom{-}5 & -8 & 3 \end{array} \right) \]

 

  1. Which of the following are linear equations? If an equation is not a linear equation, tell why.
    \[ {\bf (a)} \quad 6\,x + x\,y + 3\, z = 2; \qquad {\bf (b)} \quad 5\,a -\pi + 3\,b =0; \]
    \[ {\bf (c)} \quad \cos \left( \frac{\pi}{2} \right) x^2 -\sin (\pi )\, x\,y + 2\, z = 6; \qquad {\bf (d)} \quad \sqrt{x} -3\,y -z =1. \]
  2. Solve each system of equations.
    \[ {\bf (a)} \quad \begin{cases} 2\,x + 3\,y &= 2, \\ -4\,x-y &= 1; \end{cases} \qquad {\bf (b)} \quad \begin{cases} 2\,x + 4\,y &= -4, \\ 3\,x+ 5\,y &= 1; \end{cases} \]
  3. Find the point of intersection of the lines x −4y = −2 and 3x + 2y = 8.
  4. Solve systems of equations:
    \[ {\bf (a)} \quad \begin{split} \phantom{x} - 3\,y +4\,z&= \phantom{-}28, \\ 2\,x-8\,y + 6\,z &= -42 , \\ -5\,x +5\,y -2\,z &= \phantom{-}56; \end{split} \qquad {\bf (b)} \quad \begin{split} 2\,x - 2\,y + z&= 145, \\ 3\,x -y + 10\,z &= 203, \\ x+ 2\,y + 6\,z &= \phantom{1}58; \end{split} \]
    \[ {\bf (c)} \quad \begin{split} 2\,x - 2\,y + z &= 75, \\ \phantom{x+} 2y + 6\,z &= 30 , \\ x + 2y +2z &= 0; \end{split} \qquad {\bf (d)} \quad \begin{split} 4\,x + 5\,y -z &= 310, \\ 2x+ 3\,y + 2z &= 0, \\ 8x+ 5\,y + 4z &= 186 . \end{split} \]
  5. In the study of heat transfer, it is important to determine the steady-state temperature distribution of a thin plate when the temperature around the boundary is known (usually from an experiment or other measurement). Let us consider the plate shown in Figure below representing a cross section of a metal beam, with negligible heat flow in the direction perpendicular to the plate. Let t₁, t₂, t₃, t₄ denote the temperatures at the four interior nodes of the mesh in Figure. The temperature at a particular node is approximately equal to the average of the four nearest nodes---to the left, above, to the right, and below.

    Write a system of four equations whose solution gives estimates for the temperatures t₁, t₂, t₃, t₄.

    Temperature distribution
  6. Cubic spline interpolation provides a polynomial approximation that has smaller error than some other interpolating polynomials such as Lagrange polynomial and Newton polynomial. Suppose you need to interpolate a function f on some interval [x₁, x₂] given its values at end points f₁ = f(x₁) and f₂ = f(x₂). If you know the values of derivatives at these end points g₁ = f'(x₁) and g₂ = f'(x₂), find a system of linear equations for coefficients of cubic polynomial p(x) = 𝑎 x³ + b x² + c x + d so that this polynomial matches the values of f at end points f₁, f₂ and the values of its derivatives at end points g₁, g₂.

    Write a system of four equations for four unknowns 𝑎, b, c, and d.

  7. Suppose you are given a parabola y = 𝑎 x² + b x + c that passes through the points (x₁, y₁), (x₂, y₂), and (x₃, y₃). Determine an augmented matrix for the corresponding system of linear equations in unknowns 𝑎, b, and c.
  8. Suppose that you want to find values for 𝑎, b, and c such that the parabola y = 𝑎 x² + b x + c passes through the points (1, 2), (2, 5), and (−2, 3). Find (but do not solve) a system of linear equations whose solutions provide values for 𝑎, b, and c.
  9. In each part of the problem, find a linear system in the unknowns x₁, x₂, x₃, …, that corresponds to the given augmented matrix.
    \[ {\bf (a)} \quad \left( \begin{array}{cccc|c} -1& 3 & 2 & -7 & 8 \\ \phantom{-}2 & 1 & 0 & -8 & 7 \\ \phantom{-}6 & 8 & 3 & \phantom{-}2 & 5 \end{array} \right) , \qquad {\bf (b)} \quad \left( \begin{array}{cccc|c} \phantom{-}3& -2 & 7 & -1 & 6 \\ \phantom{-}4 & -1 & 9 & -5 & 8 \\ -1 & \phantom{-}6 & 4 & \phantom{-}9 & 2 \end{array} \right) , \]
    \[ {\bf (c)} \quad \left( \begin{array}{cccc|c} -2& 7 & -6 & \phantom{-}2 & 7 \\ \phantom{-}5 & 2 & \phantom{-}9 & -2 & 1 \\ -4 & 4 & \phantom{-}7 & \phantom{-}5 & 3 \\ \phantom{-}2 & 4 & -5 & -1 & 2 \end{array} \right) , \qquad {\bf (d)} \quad \left( \begin{array}{cccc|c} \phantom{-}8& -3 & 5 & -6 & 1 \\ \phantom{-}2 & -7 & 5 & -4 & 2 \\ -1 & \phantom{-}4 & 2 & \phantom{-}9 & 4 \\ \phantom{-}4 & \phantom{-}7 & 9 & -2 & 3 \end{array} \right) . \]
  10. In each part of the problem, find the augmented matrix for the linear system.
    \[ {\bf (a)} \quad \begin{cases} \phantom{-}3\,x_2 &= \phantom{-}6, \\ -4\,x_2 &= -8 , \\ \phantom{-}5\, x_2 &= 10; \end{cases} \qquad {\bf (b)} \quad \begin{cases} 2\,x_1 + 7\,x_2 + x_3 &= -4, \\ 9\,x_2 + 2\,x_3 &= \phantom{-}1; \end{cases} \]
    \[ {\bf (c)} \quad \begin{cases} \phantom{-}7\,x_1 - 3\,x_2 + 3\,x_3 &= -1, \\ -4\,x_1 + 6\,x_2 - 2\,x_3 &= -2 , \\ \phantom{-}5\,x_1 + 3\, x_2 - 7\,x_3 &= \phantom{-}1; \end{cases} \qquad {\bf (d)} \quad \begin{cases} \phantom{-}x_1 - 5\,x_2 + 2\,x_3 &= -3, \\ \phantom{-}3\,x_1 - 4\,x_2 + 5\,x_3 &= \phantom{-}3, \\ -4\,x_1 - 6\,x_2 + 9\,x_3 &= -5, \end{cases} \]

  1. Higham, Nicholas, Gaussian Elimination, Manchester Institute for Mathematical Sciences, School of Mathematics, The University of Manchester, 2011.
  2. Lay, D.C., Lay, S.R., McDonald, J.J., Linear Algebra and its Applications, Pearson.