Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Introduction to Linear Algebra with Mathematica
Glossary
1D Heat Equation; Diruchlet BC
We consider the initial boundary value problem for the heat equation subject to the Dirichlet boundary conditions on half line:
\begin{align} \label{eqHeat.1}
u_t &= \alpha u_{xx} - \gamma\, u + f(x,t) , & x > 0, \quad 0 < t < \infty , \\ \label{eqHeat.2}
u(0,t) &= g(t) , & 0< t < \infty , \\ \label{eqHeat.3}
u(x,0) &= u_0(x) , & x> 0 ,
\end{align}
where subscripts indicate partial derivatives. For example, \( \displaystyle \quad u_t = \frac{\partial u}{\partial t} . \quad \)
The heat equation contains (phisical) real parameters, so α > 0 and γ ≥ 0.
All functions in the heat equation \eqref{eqHeat.1}, boundary condition \eqref{eqHeat.2}, and the initial condition \eqref{eqHeat.3} are assumed to be in the Hilbert space ℌ². Also all derivatives (ut, uxx) are assumed to be continuous in the open domain 0 < x < ∞, 0 < t < ∞
To solve the given initial boundary value problem, we use sine Fourier transformation. So we multiply the differential equation \eqref{eqHeat.1} and the initial condition \eqref{eqHeat.3} by sine (kx) and integrate with respect to x from 0 to ∞. This results in the equation
\[
\frac{{\text d} u^s}{{\text d}t} = \alpha \int_0^{\infty} \frac{\partial^2 u}{\partial x^2} \,\sin (kx) \,{\text d}x - \gamma \,u^s (k,t) + f^s (k,t) ,
\]
and the initial condition
\begin{equation} \label{eqHeat.4}
u^{s} (k, +0) = u^s_0 (k) = \int_0^{\infty} u_0 (x)\,\sin (kx)\, {\text d} x
\end{equation}
for the sine Fourier transform of the unknown function
\[
u^{s} (k, t) = ℱ^s_{x \to k} \left[ u(x,t) \right] = \int_0^{\infty} u(x,t)\,\sin (kx)\,{\text d} x .
\]
The sine Fourier transforms of the given function in Eq. \eqref{eqHeat.1} is
\[
f^{s} (k, t) = ℱ^s_{x \to k} \left[ f(x,t) \right] = \int_0^{\infty} f(x,t)\,\sin (kx)\,{\text d} x .
\]
Since the differential equation contains second derivative under integration, we integrate by parts twice and obtain
\begin{align*}
\int_0^{\infty} \frac{\partial^2 u}{\partial x^2} \,\sin (kx)\,{\text d}x &=
\left. \frac{\partial u}{\partial x}\,\sin (kx) \right\vert_{x=0}^{x\to +\infty} - \int_0^{\infty} \frac{\partial u}{\partial x} \,k\, \cos (kx)\,{\text d}x
\\
&= -u(x,t)\,k\,\cos (kx) \Large\vert_{x=0}^{x\to +\infty} - \int_0^{\infty} u(x,t)\, k^2 \sin (kx)\,{\text d}x
\\
&= k\, u(+0,t) - k^2 u^s (k,t) .
\end{align*}
This leads to the the ordinary differential equation for the sine Fourier transform of the unknown function:
\begin{equation} \label{eqHeat.5}
\frac{{\text d} u^s}{{\text d}t} = - \left( \alpha\,k^2 + \gamma \right) u^s (k,t) + k\alpha\, g (t) + f^s (k, t) .
\end{equation}
We ask Mathematica to solve the initial value problem \eqref{eqHeat.5}, \eqref{eqHeat.4}.
DSolve[{u'[t] + (a*k^2 + gamma)*u[t] == F[t], u[0] == u0}, u[t], t]
{{u[t] ->
E^(-gamma t -
a k^2 t) (u0 +
Inactive[Integrate][
E^(gamma K[1] + a k^2 K[1]) F[K[1]], {K[1], 0, t}])}}
\[
u^s (k, t) = e^{- (\alpha k^2 + \gamma )t} \left[ u_0^s (k) + \int_0^t e^{ (\alpha k^2 + \gamma ) \tau} \left( k\alpha\, g (\tau ) + f^s (k, \tau ) \right) {\text d} \tau \right] .
\]
Application of the inverse sine Fourier transform to the latter gives the required solution
\[
u(x,t) = \frac{2}{\pi} \int_0^{\infty} u^s (k, t)\,\sin (kx)\,{\text d} k = I_{u0} + I_g + I_f ,
\]
where
\begin{align*}
I_{u0} &= \frac{2}{\pi} \int_0^{\infty} \sin (kx)\,e^{- (\alpha k^2 + \gamma )t} \,{\text d} k \,\int_0^{\infty} {\text d}\xi u_0 (\xi )\,\sin (k\xi ) ,
\\
&= \frac{1}{2\sqrt{\pi\alpha t}}\, e^{-\gamma t} \,\int_0^{+\infty} {\text d}\xi u_0 (\xi ) \left[ e^{- (x-\xi )^2 /(4\alpha t)} - e^{- (x+\xi )^2 /(4\alpha t)} \right]
\\
I_{g} &= \frac{2}{\pi} \int_0^{\infty} \sin (kx)\,{\text d} k \,k\alpha \, \int_0^t e^{-\gamma (t- \tau )} \,e^{- \alpha k^2 (t-\tau )} \,g(\tau ) \,{\text d} \tau
\\
&= \frac{x}{2\sqrt{\pi\alpha} } \,\int_0^{t} e^{-\gamma (t- \tau )} \, e^{-x^2 /(4\alpha (t-\tau ))} \left( t- \tau \right)^{-3/2} g(\tau )\,{\text d}\tau ,
\\
I_{f} &= \frac{2}{\pi} \int_0^{+\infty} \sin (kx)\,e^{- (\alpha k^2 + \gamma )(t- \tau )} \,{\text d} k \,\int_0^t f^s (k, \tau )\,{\text d}\tau
\\
&= \frac{2}{\pi} \int_0^{\infty} \sin (kx)\,e^{- (\alpha k^2 + \gamma )(t- \tau )} \,{\text d} k \,\int_0^t {\text d}\tau \int_0^{\infty} f(\xi , \tau )\,\sin (k\xi )\,{\text d}\xi
\\
&= \frac{1}{2\sqrt{\pi\alpha}} \int_0^{\infty} f(\xi, \tau ) \,{\text d}\xi \int_0^t {\text d}\tau \left[ e^{(x-\xi )^2 /(4\alpha (t-\tau ))} - e^{(x+\xi )^2 /(4\alpha (t-\tau ))} \right] e^{-\gamma (t-\tau )} .
\end{align*}
Integrate[Sin[k*x]*Sin[k*xi]*Exp[-a*k^2], {k, 0, Infinity}]
ConditionalExpression[((E^(-((x - xi)^2/(4 a))) -
E^(-((x + xi)^2/(4 a)))) Sqrt[\[Pi]])/(4 Sqrt[a]), Re[a] > 0]
Integrate[Exp[-a*k^2]*k*Sin[k*x], {k, 0, Infinity}]
ConditionalExpression[(E^(-(x^2/(4 a))) Sqrt[\[Pi]] x)/(4 a^(3/2)),
Re[a] > 0]
Integrate[Exp[-a*k^2]*Sin[k*x]*Sin[k*xi], {k, 0, Infinity}]
ConditionalExpression[((E^(-((x - xi)^2/(4 a))) -
E^(-((x + xi)^2/(4 a)))) Sqrt[\[Pi]])/(4 Sqrt[a]), Re[a] > 0]
We integrate by parts each integral:
\begin{align*}
I_{u0} &= \frac{2}{\pi} \int_0^{\infty} \sin (kx)\,e^{- (\alpha k^2 + \gamma )t} \,{\text d} k \,\int_0^{\infty} {\text d}\xi u_0 (\xi )\,\frac{\text d}{{\text d}\xi} \left( -\frac{\cos (k\xi )}{k} \right)
\\
&= \frac{2}{\pi} \int_0^{\infty} \sin (kx)\,e^{- (\alpha k^2 + \gamma )t} \,{\text d} k \left[ -\left. u_0 (\xi )\, \frac{\cos (k\xi )}{k} \right\vert_{\xi =0}^{+\infty} + \int_0^{+\infty} \frac{\cos (k\xi )}{k} \, \frac{{\text d} u_0 }{{\text d}\xi}\,{\text d}\xi \right]
\\
&= \frac{2}{\pi}\, u_0 (+0) \,\int_0^{\infty} \frac{\sin (kx)}{k}\,e^{- (\alpha k^2 + \gamma )t} \,{\text d} k + \frac{2}{\pi} \int_0^{\infty} \sin (kx)\,e^{- (\alpha k^2 + \gamma )t} \,{\text d} k \,\int_0^{+\infty} \frac{\cos (k\xi )}{k} \, \frac{{\text d} u_0 }{{\text d}\xi}\,{\text d}\xi
\\
&= u_0 (+0)\,e^{-\gamma t}\,\mbox{erf} \left( \frac{x}{2\sqrt{\alpha t}} \right) + \frac{1}{2} \, \int_0^{+\infty} {\text d}\xi \left[ \mbox{erf} \left( \frac{x - \xi}{2\sqrt{\alpha t}} \right) + \mbox{erf} \left( \frac{x + \xi}{2\sqrt{\alpha t}} \right) \right] \frac{{\text d} u_0 }{{\text d}\xi} ,
\end{align*}
Integrate[Sin[k*x]*Exp[-a*k^2]/k, {k, 0, Infinity}]
ConditionalExpression[1/2 \[Pi] Erf[x/(2 Sqrt[a])], Re[a] > 0]
Integrate[Sin[k*x]*Cos[k*xi]*Exp[-a*k^2]/k, {k, 0, Infinity}]
ConditionalExpression[
1/4 \[Pi] (Erf[(x - xi)/(2 Sqrt[a])] + Erf[(x + xi)/(2 Sqrt[a])]),
Re[a] > 0]
where
\[
\mbox{erf} (t) = \frac{2}{\sqrt{\pi}}\,\int_0^t e^{-\eta^2} \,{\text d}\eta
\]
is the error function. Since x²/t has no limit as x,t approach zero, the integral Iu0(x, t) has not limit value at the origin unless uNext we make a substitution in integral Ig
\[
\tau = t - \frac{x^2}{4\alpha T} \qquad \Longrightarrow \qquad {\text d}\tau =\frac{x^2}{4\alpha T^2} \,{\text d}T .
\]
This yields
\begin{align*}
I_{g} (x, t) &= \frac{x}{2\sqrt{\pi\alpha} } \,\int_0^{t} e^{-\gamma (t- \tau )} \, e^{-x^2 /(4\alpha (t-\tau ))} \left( t- \tau \right)^{-3/2} g(\tau )\,{\text d}\tau
\\
&= \frac{x}{2\sqrt{\pi\alpha}} \,\int_{x^2/(4\alpha t)}^{+\infty} e^{-\gamma x^2 /(4\alpha T)} \, e^{-T} \left( \frac{4 \alpha T}{x^2} \right)^{3/2} \,\frac{x^2}{4\alpha T^2} \,g \left( t - \frac{x^2}{4\alpha T} \right) {\text d}T
\\
&= \frac{1}{\sqrt{\pi}} \, \int_{x^2/(4\alpha t)}^{+\infty} e^{-\gamma x^2 /(4\alpha T)} \, e^{-T} \, g \left( t - \frac{x^2}{4\alpha T} \right) \frac{{\text d}T}{\sqrt{T}} .
\end{align*}
Upon adding and subtructing g(t), we transfer the integral to the following form:
\[
I_g (x,t) = \frac{g(t)}{\sqrt{\pi}} \, \int_{x^2/(4\alpha t)}^{+\infty} e^{-\gamma x^2 /(4\alpha T)} \, e^{-T} \,\frac{{\text d}T}{\sqrt{T}} + \frac{1}{\sqrt{\pi}} \, \int_{x^2/(4\alpha t)}^{+\infty} e^{-\gamma x^2 /(4\alpha T)} \, e^{-T} \left[ g \left( t - \frac{x^2}{4\alpha T} \right) - g(t) \right] \frac{{\text d}T}{\sqrt{T}} .
\]
Using Mathematica, we simplify tis expression
Integrate[
Exp[-gamma*x^2 /(4*a*t)]*Exp[-T]/Sqrt[T], {T, x^2 /(4*a*t),
Infinity}]/Sqrt[Pi]
E^(-((gamma x^2)/(4 a t))) Erfc[1/2 Sqrt[x^2/(a t)]]
\[
I_g (x,t) = g(t)\, e^{- \gamma \,x^2 /(4\alpha t)} \,\mbox{erf}\left( \frac{x}{2\sqrt{\alpha t}} \right) + \frac{1}{\sqrt{\pi}} \, \int_{x^2/(4\alpha t)}^{+\infty} e^{-\gamma x^2 /(4\alpha T)} \, e^{-T} \left[ g \left( t - \frac{x^2}{4\alpha T} \right) - g(t) \right] \frac{{\text d}T}{\sqrt{T}} .
\]
In integrals Iu0 and If we make substitution span class="math">\( \displaystyle \quad \xi \pm x = X\.\sqrt{4\alpha t} ; \quad \) this yields
\begin{align*}
I_{u0} (x,t) &= \frac{1}{2\sqrt{\pi\alpha t}}\, e^{-\gamma t} \,\int_0^{+\infty} {\text d}\xi \,u_0 (\xi ) \left[ e^{- (x-\xi )^2 /(4\alpha t)} - e^{- (x+\xi )^2 /(4\alpha t)} \right]
\\
&= e^{-\gamma t} \,\int_{-x/\sqrt{4\alpha t}}^{+\infty} \, e^{-X} \, u_0 \left( x + X\,\sqrt{4\alpha t} \right) {\text d}X - e^{-\gamma t} \,\int_{x/\sqrt{4\alpha t}}^{+\infty} \, e^{-X} \, u_0 \left( -x + X\,\sqrt{4\alpha t} \right) {\text d}X ;
\end{align*}
and
\begin{align*}
I_{f} (x,t) &=
\frac{1}{2\sqrt{\pi\alpha}} \int_0^{\infty} f(\xi, \tau ) \,{\text d}\xi \int_{-x/\sqrt{4\alpha t}}^t {\text d}\tau \left[ e^{(x-\xi )^2 /(4\alpha (t-\tau ))} - e^{(x+\xi )^2 /(4\alpha (t-\tau ))} \right] e^{-\gamma (t-\tau )} .
\\
&= \int_0^t {\text d}\tau \,e^{-\gamma (t-\tau )} \left[ \int_{-x/\sqrt{4\alpha t}}^{\infty} {\text d}X \, f \left( x + X\,\sqrt{4\alpha t} \right) e^{-X} -
\int_{x/\sqrt{4\alpha t}}^{\infty} {\text d}X \, f \left( -x + X\,\sqrt{4\alpha t} \right) e^{-X} e^{-X} \right] .
\end{align*}
Numerical Experiment
We calculate upon evaluation integrals with pecewise input constant functions. Let us start with u₀.
\[
u_0 (x) = \begin{cases}
1 , & \quad\mbox{if} \quad 0 \le x \le 1 , \\
0, & \quad \mbox{otherwise} .
\end{cases}
\]
Integrate[
Exp[-(x - xi)^2 /4/t] - Exp[-(x + xi)^2 /4/t], {xi, 0, 1}]/(2*
Sqrt[Pi*t])
1/2 (-Erf[(-1 + x)/(2 Sqrt[t])] + 2 Erf[x/(2 Sqrt[t])] -
Erf[(1 + x)/(2 Sqrt[t])])
\[
I_0 (x,t) = \mbox{erf} \left( \frac{x}{2\sqrt{t}} \right) - \frac{1}{2}\,\mbox{erf} \left( \frac{x-1}{2\sqrt{t}} \right) - \frac{1}{2}\,\mbox{erf} \left( \frac{1+x}{2 \sqrt{t}} \right) ,
\]
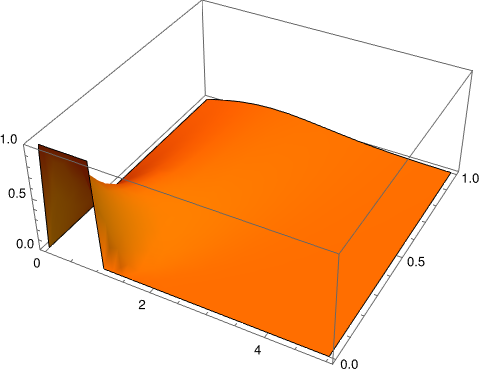
wjere erf is the error function. We plot the function
Plot3D[1/
2 (-Erf[(-1 + x)/(2 Sqrt[t])] + 2 Erf[x/(2 Sqrt[t])] -
Erf[(1 + x)/(2 Sqrt[t])]), {x, 0, 5}, {t, 0, 1},
PlotStyle -> Orange, Mesh -> None, PlotRange -> {0, 1}]
As it is seen from the graph, the corresponding integral I0(x, t) is unbounded at x = 0. To check the problem, we consider another initial function that vanishes at the origin:
\[
u_0 (x) = \begin{cases}
1 , & \quad\mbox{if} \quad 0.5 \le x \le 1.5 , \\
0, & \quad \mbox{otherwise} .
\end{cases}
\]
Integrate[
Exp[-(x - xi)^2 /4/t] - Exp[-(x + xi)^2 /4/t], {xi, 0, 1}]/(2*
Sqrt[Pi*t])
1/2 (-Erf[(-3 + 2 x)/(4 Sqrt[t])] + Erf[(-1 + 2 x)/(4 Sqrt[t])] +
Erf[(1 + 2 x)/(4 Sqrt[t])] - Erf[(3 + 2 x)/(4 Sqrt[t])])
\[
I_0 (x,t) = \frac{1}{2}\,\mbox{erf} \left( \frac{2x-1}{4\sqrt{t}} \right) - \frac{1}{2}\,\mbox{erf} \left( \frac{2x-3}{4\sqrt{t}} \right) +
\frac{1}{2}\,\mbox{erf} \left( \frac{2x+1}{4\sqrt{t}} \right)
- \frac{1}{2}\,\mbox{erf} \left( \frac{2x+3}{4 \sqrt{t}} \right) ,
\]
wjere erf is the error function. We plot the function
Plot3D[1/
2 (-Erf[(-3 + 2 x)/(4 Sqrt[t])] + Erf[(-1 + 2 x)/(4 Sqrt[t])] +
Erf[(1 + 2 x)/(4 Sqrt[t])] - Erf[(3 + 2 x)/(4 Sqrt[t])]),
{x, 0, 5}, {t, 0, 1},
PlotStyle -> Orange, Mesh -> None, PlotRange -> {0, 1}]
Now we consider function ug, where g is again fiecewise constant.
(x/2/Sqrt[Pi])*
Integrate[
Exp[-(t - tau)]*Exp[-x^2/4/(t - tau)]/(t - tau)^(3/2), {tau, 0,
Max[1, t]}]
1/(2 Sqrt[x^2])E^-Sqrt[
x^2] x (-Erfc[-((-2 t + Sqrt[x^2])/(2 Sqrt[t]))] +
Erfc[(2 t - Sqrt[x^2] - 2 Max[1, t])/(2 Sqrt[t - Max[1, t]])] +
E^(2 Sqrt[
x^2]) (Erfc[(2 t + Sqrt[x^2])/(2 Sqrt[t])] -
Erfc[(2 t + Sqrt[x^2] - 2 Max[1, t])/(2 Sqrt[t - Max[1, t]])])
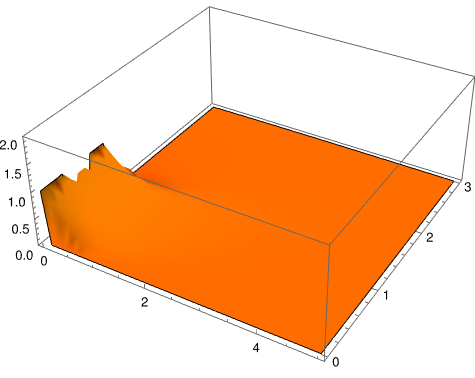
Since this expression is cumbersome, we use numerical integration. Note that the integrand has a weak singularity as 1/√X as X → 0.
Plot3D[(x/2/Sqrt[Pi])*
NIntegrate[
Exp[-(t - tau)]*Exp[-x^2/4/(t - tau)]/(t - tau)^(3/2), {tau, 0,
Min[1, t]}], {x, 0, 5}, {t, 0, 3}, PlotStyle -> Purple,
Mesh -> None, PlotRange -> {0, 2}]
\[
f (x,t) = \begin{cases}
f(t) , & \quad \mbox{if} \quad 0 \le x \le 1 , \\
0 , & \quad \mbox{otherwise}.
\end{cases}
\]
We substitute the intermedian integral (with α = 1 for simplicity)
(1/2/Sqrt[Pi])*
Integrate[
Exp[(x - xi)^2 /4/(t - tau)] - Exp[(x + xi)^2 /4/(t - tau)] , {xi,
0, 1}]
-1/2 Sqrt[
t - tau] (Erfi[(-1 + x)/(2 Sqrt[t - tau])] -
2 Erfi[x/(2 Sqrt[t - tau])] + Erfi[(1 + x)/(2 Sqrt[t - tau])])
into the general formula,
\[
I_f (x, t) = \int_0^t f(\tau )\,{\text d}\tau \left\{ \frac{1}{\sqrt{t - \tau}} \left[ \mbox{erf} \left( \frac{x}{2\sqrt{t - \tau}} \right) - \frac{1}{2} \,\mbox{erf} \left( \frac{x-1}{2\sqrt{t - \tau}} \right) - \frac{1}{2} \,\mbox{erf} \left( \frac{x+1}{2\sqrt{t - \tau}} \right) \right]
\right\} .
\tag{f.1}
\]
For numerical integration, we intrduce ε = 0.1 amd integrate with respect to τ from 0 to t − ε because the integrand approach 0 exponentially near τ = t; so
\[
I_f (x, t) = \int_0^{t-\epsilon} f(\tau )\,{\text d}\tau \left\{ \frac{1}{\sqrt{t - \tau}} \left[ \mbox{erf} \left( \frac{x}{2\sqrt{t - \tau}} \right) - \frac{1}{2} \,\mbox{erf} \left( \frac{x-1}{2\sqrt{t - \tau}} \right) - \frac{1}{2} \,\mbox{erf} \left( \frac{x+1}{2\sqrt{t - \tau}} \right) \right]
\right\} .
\tag{f.2}
\]
Upon choosing f(t) = χ[0, 2] (t), we obtain
Plot3D[ NIntegrate[ -(1/2) Sqrt[
t - tau] (Erfi[(-1 + x)/(2 Sqrt[t - tau])] -
2 Erfi[x/(2 Sqrt[t - tau])] +
Erfi[(1 + x)/(2 Sqrt[t - tau])]), {tau, 0, Min[2, t - 0.1]}], {x,
0, 5}, {t, 0.1, 3}, PlotStyle -> Brown, Mesh -> None,
PlotRange -> {0, 1}]
Boundary operator
- Boyd, J.P. and Flyer, N., Compatibility conditions for time-dependent partial differential equations and the rate of convergence of Chebyshev and Fourier spectral methods, Computer Methods in Applied Mechanics and Engineering, 1999, Volume 175, Issues 3–4, Pages 281--309. https://doi.org/10.1016/S0045-7825(98)00358-2
- Chatziafratis, A., Boundary behaviour of the solution of the heat equation on the half line via the Fokas unified transform method, 2024, https://doi.org/10.48550/arXiv.2401.08331
- Chatziafratis, A., Fokas, A., Aifantis, E.C., Variations of heat equation on the half-line via the Fokas method, 2024, First published: 08 September 2024 https://doi.org/10.1002/mma.10303
- Chatziafratis, A., Mantzavinos, D., Boundary behavior for the heat equation on the half-line, 2022, https://doi.org/10.1002/mma.8245
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Basic Concepts
Return to the Part 2 Fourier Series
Return to the Part 3 Integral Transformations
Return to the Part 4 Parabolic PDEs
Return to the Part 5 Hyperbolic PDEs
Return to the Part 6 Elliptic PDEs
Return to the Part 6P Potential Theory
Return to the Part 7 Numerical Methods