The main advantage of the Laplace transform method compared to other methods is its simplicity of handling constant coefficient differential equations with intermittent input functions.
This section demonstrates application of the Laplace transform to such differential equations.
We demonstrate advantages of the Laplace transform in solving differential equations with discontinuous inputs. Although the variation of parameters method still works in this case, its practical implementation becomes cumbersome. In contrast, you will see that the Laplace transform handles intermittent input functions almost naturally. A user is recommended to go through examples.
In electrical and mechanical applications, it is common to consider systems that are subject to discontinuous or piecewise continuous forcing functions. For instance, a circuit might be subjected to an applied DC voltage that is held constant at 12 volts for some time and then shut off (i.e., reduced to zero for all subsequent time). Or, one might come home and start using a vacuum cleaner that consumes an alternating voltage source for a certain period of time and then shuts it off, or starts using another electrical device like a coffee maker. Almost all engineering problems lead to piecewise continuous forcing functions, as ON/OFF or stop/start is a major design consideration. Music synthesizers and modeling violins and pianos are clear examples of this stop, start, and change nature in manipulating sound waves.
Abruptly changing input functions are simply seen everywhere in our world. The vast field of impact theory has applications including the optimization of processing materials, impact testing, and visualizing the dynamics of granular media. Impact theory has vast applications in the automotive, military, and medical industries, including studies of the biomechanics of the human body, particularly the hip and knee joints. Other medical applications include studies of neural oscillations (brainwaves) in the spatial distribution and cellular-synaptic generation of hippocampal sharp waves. In traditional aerodynamics, the propagation of shock waves in any media is invariably associated with instantaneous increases in pressure and temperature behind the shock wave. Aircraft landing, road traffic accidents, and the analysis of car outputs on bumping roads also necessarily rely on studying these functions.
A function f (t ), defined on a semi-infinite interval [0, ∞), is called piecewise continuous or intermittent if this interval can be broken into a finite number of subintervals
\[
[0, \infty ) = [0, b_1) \cup (a_2 , b_2 ) \cup \cdots \cup (a_m, \infty ) ,
\]
so that the function
f (
t ) is continuous on each of them and has finite limit values at the endpoints. A piecewise continuous function can be defined as
\begin{equation} \label{EqInput.3}
f(t) = \begin{cases}
f_1 (t) , & \ 0 < t < b_1 ,
\\
f_2 (t) , & \ a_2 < t < b_2 ,
\\
\vdots
\\
f_m (t) , & a_m < t < \infty ,
\end{cases}
\end{equation}
where each function
f k (
t ),
k = 1, 2, … ,
m , is continuous on the interval (𝑎
k ,
b k ) and has finite limit values at 𝑎
k and
b k . Since we are going to apply the Laplace transformation to these intermittent functions, we require that the function
f m (
t ) grows no faster than the exponential function at infinity in order to define its Laplace transform:
\begin{equation} \label{EqInput.1}
f^L (\lambda ) = \left( {\cal L} \,f \right) (\lambda ) = \int_0^{\infty} f(t)\,e^{-\lambda t} \,{\text d} t .
\end{equation}
We usually do not specify the values of the piecewise continuous functions at the points of discontinuity (if any) because they do not effect the value of Laplace's integral \eqref{EqInput.1}. However, the inverse Laplace transformation always defines the value of the function at the point of discontinuity to be the mean value of its left and right limit values. Therefore, all used intermittent functions are assumed to posses this mean value property at the points of discontinuity.
The Laplace transformation exists for many functions of a positive real variable (usually associated with time) including discontinuous functions.
Of course, the Laplace transform does not exist for arbitrary functions, but only for those that belong to special classes. Previously, we identified that the Laplace transform exists for functions with finite jumps and that grow no faster than an exponential function at infinity. The algorithm for finding a Laplace transform of an intermittent function consists
of two steps:
Rewrite the given piecewise continuous function through shifted Heaviside functions.
Use the shift rule \( {\cal L} \left[ H(t-a)\, f(t-a) \right] = e^{a\lambda}\, {\cal L} \left[ f(t) \right] , \quad a > 0. \)
Differential Equations with Discontinuous Forcing Functions
Our main objective is to solve linear differential equations with
intermittent forcing functions
\begin{equation} \label{EqInput.6}
L \left[ \,\texttt{D}\,\right] y (t) = f(t) , \qquad L \left[ \,\texttt{D}\,\right] = a_n \texttt{D}^n + a_{n-1} \texttt{D}^{n-1} + \cdots + a_1 \texttt{D} + a_0 \texttt{I} , \quad \texttt{D} = \frac{\text d}{{\text d}t} ,
\end{equation}
where
f (
t ) is a piecewise continuous function \eqref{EqInput.3}. Application of the Laplace transformation for solving differential equations of the form \eqref{EqInput.6} was shown in the previous section, and the procedure remains the same, independently of whether the forcing function
f (
t ) is continuous or intermittent. Since the forcing function may contain one or more discontinuities, the solution of the corresponding initial value problem does not possess the required number of continuous derivatives. This means that we must adjust our definition of solution to this case.
Theorem 1:
Suppose that 𝑎 ≠ 0,
b , and
c are constants, and
f (
t ) is a piecewise continuous function on [0, ∞), with finite jump discontinuities at
t 1 ,
t 2 , …,
t n , where
\[
0 < t_1 < t_2 < \cdots < t_n .
\]
Let
y 0 and
y 1 be arbitrary real numbers. Then there is a unique function
y (
t ) defined on [0, ∞) with the following properties:
We illustrate the Laplace transform technique in the numerous examples. To demonstrate the influence of the forcing function, some examples contain several versions of the initial value problem.
Example 1: First order differential equation: RL- and RC-circuits
Example 1:
Let us consider a RC-circuit.
We recall that the
voltage v across a
capacitor is related to the
electric charge q by
v =
Sq , where
S = 1/
C is the
elastance , the inverse of
capacitance . The terms elastance and elastivity were coined by
Oliver Heaviside in 1886. Since the current is
i = d
q /d
t , an integration gives
\[
v = \frac{1}{C}\,q = Sq = S \int_0^t i(t)\,{\text d}t + S q(0) .
\]
In most cases, the initial charge is zero.
Resistance is the capacity of materials to impede the flow of current or, more specifically, the flow of electric charge. The circuit element used to model this behavior is the resistor . Most materials exhibit a measurable resistance to current. The amount of resistance depends on the material. Metals such as copper and aluminum have small values of resistance, making them good choices for wiring used to conduct electric current. In fact, when represented in a circuit diagram, copper or aluminum wiring isn't usually modeled as a resistor: the resistance of the wire is so small compared to the resistance of other elements in the circuit that we can neglect the wiring resistance to simplify the diagram.
For purposes of current analysis, we must reference the current in the resistor to the terminal voltage. We can do so in two ways: either in the direction of the voltage drop across the resistor or in the direction of the voltage rise across the resistor. If we choose the former, the relationship between the voltage and current is
\[
v = i\,R.
\]
A resistor–capacitor circuit (RC circuit ) is an electric circuit composed of resistors and capacitors . It may be driven by a voltage or current source and these will produce different responses. When a voltage source is applied to an RC circuit, the capacitor, C charges up through the resistance, R . In a RC circuit, a capacitor is connected in series with a resistor of resistance R and a source of voltage v (t ), the voltage equation is
\[
R\,i + \frac{1}{C} \int_0^t i(t)\,{\text d}t = v(t) \qquad \Longrightarrow \qquad R\,\frac{{\text d}q}{{\text d}t} + S\, q = f(t) .
\]
If we denote by y (t ) the charge in the circuit, then this function satisfies (with appropriate scaling factors of capacitance and resistor) the first order inhomogeneous equation
\[
\dot{y} + 4\,y(t) = f( t), \qquad y(0) = 1,
\tag{1.1}
\]
where the input function steadily ramps up, then keeps constant and suddenly is removed:
\[
f(t) = \begin{cases}
t, & \ \mbox{ when } \ 0 < t < 1,
\\
1 , & \ \mbox{ when } \ 1 < t < 3,
\\
0, & \ \mbox{ for }\ t> 3 .
\end{cases}
\tag{1.2}
\]
Since the Laplace transform of the input function
f (
t ) is
\[
f^L (\lambda ) = \int_0^1 t\,e^{-\lambda t}{\text d}t + \int_1^3 e^{-\lambda t}{\text d}t = \frac{1}{\lambda^2} - \frac{1}{\lambda^2}\, e^{-\lambda} - \frac{1}{\lambda}\, e^{-3\lambda} ,
\]
it is reasonable to apply the Laplace transformation to the given IVP (1.1). This yields
Simplify[Integrate[t*Exp[-s*t], {t, 0, 1}] + Integrate[Exp[-s*t], {t, 1, 3}]]
-(-1 + E^-s + E^(-3 s) s)/s^2
\[
y^L = \frac{1}{\lambda +4} + \frac{1}{\lambda +4}\, f^L (\lambda ) = \frac{1}{\lambda +4} + \frac{1}{\lambda +4}\left[ \frac{1}{\lambda^2} - \frac{1}{\lambda^2}\, e^{-\lambda} - \frac{1}{\lambda}\, e^{-3\lambda} \right] .
\tag{1.3}
\]
In order to determine the explicit formula for
y (
t ), we apply the inverse Laplace transform to every term in Eq.(1.3).
\begin{align*}
y_h (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda +4} \right] = e^{-4t} H(t) ,
\\
y_1 (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda +4}\, \frac{1}{\lambda^2} \right] = \frac{1}{16} \left[ 4t -1 + e^{-4t} \right] H(t) ,
\\
y_2 (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda +4}\,\frac{-1}{\lambda^2}\, e^{-\lambda} \right] = g_2 (t-1) ,
\\
y_3 (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda +4}\,\,\frac{-1}{\lambda}\, e^{-3\lambda} \right] = g_3 (t-3) ,
\end{align*}
where
\begin{align*}
g_2 (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda +4}\,\frac{-1}{\lambda^2} \right] = \frac{-1}{16} \left[ 4t -1 + e^{-4t} \right] H(t) ,
\\
g_3 (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda +4}\,\,\frac{-1}{\lambda} \right] = \frac{-1}{4} \left[ 1 - e^{-4t} \right] H(t) .
\end{align*}
We ask
Mathematica for help:
InverseLaplaceTransform[1/(s + 4)/s^2, s, t]
-(1/16) + E^(-4 t)/16 + t/4
InverseLaplaceTransform[1/(s + 4)/s, s, t]
1/4 - E^(-4 t)/4
We plot the the solution (in blue) along with the input function f (t ) in black.
yh[t_] = Exp[-4*t]
Plot of the solution (in blue), and the input function f (t ) in black.
Mathematica code
We plot the derivative of the solution (in purple). As it is seen from the graph, the derivative has a finite jump of discontinuity, but the solution is a continuous function.
yh[t_] = Exp[-4*t]
Plot of the derivative of the solution (in purple).
Mathematica code
⁎ ✱ ✲ ✳ ✺ ✻ ✼
✽ ❋ ===========================================
Now we consider a RL-circuit.
We plot the RL-circuit:
coil = ParametricPlot[{0.8*Cos[9*t] + 2.6*t, 0.8*Sin[9*t]}, {t, -0.35,
4.88}, PlotStyle -> Thickness[0.01]];
RL-circuit.
Mathematica code
This leads to the similar first order differential equation
\[
\dot{y} + 4\,y(t) = f( t), \qquad y(0) = 1,
\tag{1.4}
\]
where the input function steadily ramps up, then keeps constant and finally suddenly is removed:
\[
f(t) = \begin{cases}
0, & \ \mbox{ when } \ 0 < t < 1,
\\
t-1, & \ \mbox{ when } \ 1 < t < 2,
\\
1 , & \ \mbox{ when } \ 2 < t < 3,
\\
4-t , & \ \mbox{ when } \ 3 < t < 4,
\\
0, & \ \mbox{ for }\ t> 4 .
\end{cases}
\tag{1.5}
\]
Here
y (
t ) denotes the current in the circuit. In order to apply the Laplace transformation to the given initial value problem (1.4), we rewrite the input function(1.5) in appropriate form that is ready to apply the shift rule:
\[
f(t) = \left( t-1 \right) \left[ H(t-1) - H(t-2) \right] + H(t-2) - H(t-3) + \left( 4-t \right) \left[ H(t-3) - H(t-4) \right] .
\]
Using some simplifications, we get
\[
f(t) = \left( t-1 \right) H(t-1) - \left( t-2 \right) H(t-2) - \left( t-3 \right) H(t-3) + \left( t-4 \right) H(t-4) .
\]
Its Laplace transform is
\[
f^L (\lambda ) = \frac{1}{\lambda^2} \left[ e^{-\lambda} - e^{-2\lambda} - e^{-3\lambda} + e^{-3\lambda} \right] .
\]
Then application of the Laplace transformation to the IVP (1.4) yields
\[
y^L (\lambda ) = \frac{1}{\lambda +4} + \frac{1}{\lambda +4} \, f^L = \frac{1}{\lambda +4} + \frac{1}{\lambda^2 (\lambda +4)}\left[ e^{-\lambda} - e^{-2\lambda} - e^{-3\lambda} + e^{-3\lambda} \right] .
\]
Since the inverse Laplace transform of two main terms is
\[
{\cal L}^{-1} \left[ \frac{1}{\lambda +4} \right] = e^{-4t} H(t)
\]
and
\[
g(t) = {\cal L}^{-1} \left[ \frac{1}{\lambda^2 (\lambda +4)} \right] = \frac{1}{16} \left[ 4t -1 + e^{-4t} \right] H(t) ,
\]
InverseLaplaceTransform[(1)/(s + 4)/s^2, s, t]
-(1/16) + E^(-4 t)/16 + t/4
we find the required solution of the given IVP (1.4) to be
\[
y(t) = e^{-4t} H(t) + g(t-1) - g(t-2) - g(t-3) + g(t-4) .
\]
■
Example 2: Mixing problem with valved input
Example 2:
Consider a large reservoir containing 2000 liters (L for short) of water that has two holes. One hole has a valve and it is used for incoming mixer and the liquid is leaving through another hole. At time
t = 0, the valve is open, delivering 5 L/min of a brine solution containing 0.4 kg of salt per liter. At
t = 30 min, the valve is switched into another position, delivering 5 L/min of brine at a concentration 0.2 kg/L. Initially, 20 kg of salt are dissolved in 2000 L of water in the tank. The exit valve, which empties the reservoir at 5 L/min, maintains the contents of the tank at constant volume. Assuming the solution is kept well stirred, determine the amount of salt in the reservoir at all times
t > 0.
circle = Graphics[{Thick, Circle[{0, 0}, 0.5, {1.89, 4.39}]}];
Mixing tank with valve open in one side.
Mathematica code
Let x (t ) be the amount of salt (in kilograms) in the reservoir at time t . Then the ratio x (t )/2000 is the concentration in kilograms per liter. The salt content is depleted at the rate (5 L/min) × (x (t )/2000 kg/L) = x (t )/500 kg/min through the exit valve. Simultaneously, it is enriched through another valve at the rate f (t ) given by
\[
f(t) = \begin{cases}
0.4\mbox{ kg/L } \times 5\mbox{ L/min } = 2.0\mbox{ kg/min}, & \ 0 < t < 30,
\\
0.2\mbox{ kg/L } \times 5\mbox{ L/min } = 1.0\mbox{ kg/min}, & \ t > 30 .
\end{cases}
\]
Hence,
x (
t ) changes at a rate
\[
\frac{{\text d}x(t)}{{\text d}t} = f(t) - \frac{x(t)}{500} , \qquad x(0) = 20.
\tag{2.1}
\]
To solve the initial value problem (2.1) using the techniques of
Part II , we would have to break up the time interval [0, ∞) into two subintervals [0, 30) and (30, ∞). On these subintervals, the nonhomogeneous term
f (
t ) is constant, and the separation of variables is called to determine the solution at each subinterval. One arbitrary constant could be determined from the initial condition on the interval [0, 30). Its solution then would be used to identify another arbitrary constant for the solution on subinterval (30, ∞).
Of course, this example is used to illustrate a new approach using Laplace transformation. The latter offers several advantages over the previous techniques.
First, we rewrite the input function f (t ) as
\[
f(t) = 2 \left[ H(t) - H(t-30) \right] + H(t-30) = 2\, H(t) - H(t-30) .
\]
Then its Laplace transform becomes
\[
f^L (\lambda ) = {\cal L} \left[ f(t) \right) = \int_0^{\infty} f(t)\,e^{-\lambda t} {\text d}t = \frac{1}{\lambda} \left( 2 - e^{-30\lambda} \right) .
\]
We multiply both sides of Eq.(2.1) by
e −λt and integrate with respect to
t from 0 to ∞. This leads to the algebraic equation for
x L , the Laplace transform of
x (
t ):
\[
\lambda \, x^L -20 = f^L - \frac{x^L}{500} \qquad \Longrightarrow \qquad x^L (\lambda ) = \frac{20}{\lambda +1/500} + \frac{1}{\lambda +1/500} \cdot f^L .
\]
So we see that the Laplace transform
y L is the sum of two terms:
\[
x^L (\lambda ) = x_h^L (\lambda ) + x_p^L (\lambda ) , \qquad \mbox{with} \qquad x_h^L = \frac{20}{\lambda +1/500} , \quad x_p^L = \frac{1}{\lambda +1/500} \cdot f^L .
\]
The inverse Laplace transform of the former is
\[
x_h (t) = {\cal L}^{-1} \left[ x_h^L (\lambda ) \right] = {\cal L}^{-1} \left[ \frac{20}{\lambda +1/500} \right] = 20\, e^{-t/500} H(t) ,
\]
which is the solution of the homogeneous equation with the given initial condition:
\[
\dot{x} + x(t)/500 = 0, \qquad x(0) = 20.
\]
For determination of
\[
x_p (t) = {\cal L}^{-1} \left[ x_p^L (\lambda ) \right] = {\cal L}^{-1} \left[ \frac{1}{\lambda +1/500} \cdot f^L \right]
\]
we have two options and we demonstrate both of them. First, we use the convolution rule:
\[
x_p (t) = g(t) \ast f(t) = \int_0^t e^{-(t-\tau )/500} f(\tau )\,{\text d}\tau ,
\]
where
\[
g(t) = {\cal L}^{-1} \left[ \frac{1}{\lambda +1/500} \right] = e^{-t/500} H(t)
\]
is the Green function for the given differential equation (2.1). Then
\[
y_p (t) = 2 \int_0^t e^{-(t-\tau )/500} \,{\text d}\tau - H(t-30) \int_{30}^t e^{-(t-\tau )/500} \,{\text d}\tau = 500 \left( 1 - e^{-t/500} \right) H(t) - 500 \left( 1 - e^{(30-t)/500} \right) H(t-30) .
\]
Integrate[Exp[-(t - s)/500], {s, 0, t}]
500 - 500 E^(-t/500)
Integrate[Exp[-(t - s)/500], {s, 30, t}]
500 - 500 E^(3/50 - t/500)
Now we demonstrate another approach that is based on using the explicit formula for
f L :
\[
y_p (t) = {\cal L}^{-1} \left[ \frac{1}{\lambda +1/500} \cdot \frac{1}{\lambda} \left( 2 - e^{-30\lambda} \right) \right] .
\]
According the shift rule, we have
\[
y_p (t) = 2\,p(t) - p(t-30) \qquad \mbox{where} \quad p(t) = {\cal L}^{-1} \left[ \frac{1}{\lambda +1/500} \cdot \frac{1}{\lambda} \right] = 500 \left( 1 - e^{-t/500} \right) H(t) .
\]
Although we can find the explicit expression for function
p (
t ) with the aid of the residue theorem, we prefer to delegate this job to
Mathematica :
InverseLaplaceTransform[1/(s + 1/500)/s, s, t]
500 - 500 E^(-t/500)
■
Example 3: Vibration of a string-mass system by a strike
Example 3:
A mass attached to a string is released with the initial velocity below the equilibrium position for the mass-spring system and begins to vibrate. After π seconds the mass is struck by a hammer exerting an impulse on the mass. The system is governed by the symbolic initial value problem
\[
\ddot{y} + 4\,y(t) = \delta( t - \pi ), \qquad y(0) = -1, \quad \dot{y}(0) = 1.
\tag{3.1}
\]
Here
y (
t ) denotes the displacement from the equilibrium position at time
t = 0. Applying the Laplace transform, we convert the given IVP (2.1) into the algebraic equation:
\[
\lambda^2 y^L -\dot{y}(0) - \lambda\,y(0) + 4\,y^L = e^{-\pi\lambda} .
\]
Substituting the given initial values, we obtain
\[
y^L (\lambda ) = {\cal L} \left[ y(t) \right] = \int_0^{\infty} y(t)\,e^{-\lambda t} {\text d} t = \frac{1-\lambda}{\lambda^2 + 4} + \frac{1}{\lambda^2 + 4}\, e^{-\pi\lambda} .
\tag{3.2}
\]
Taking the inverse Laplace transform, we get the required solution as the sum of two functions:
\[
y(t) - y_h (t) + y_p (t)
\tag{3.3}
\]
where
\[
y_h (t) = {\cal L}^{-1} \left[ \frac{1-\lambda}{\lambda^2 + 4} \right] = \left[ \frac{1}{2}\, \sin (2t) - \cos (2t) \right] H(t)
\tag{3.4}
\]
is the solution of the homogeneous equation subject to the given initial conditions.
InverseLaplaceTransform[(1 - s)/(s^2 + 4), s, t]
1/2 (-2 Cos[2 t] + Sin[2 t])
Another function,
\[
y_p (t) = {\cal L}^{-1} \left[ \frac{1}{\lambda^2 + 4} \, e^{-\pi\lambda} \right] = g(t-\pi )
\tag{3.5}
\]
is the solution of the inhomogeneous equation subject to the homogeneous initial conditions:
\[
\ddot{y} + 4\,y(t) = \delta( t - \pi ), \qquad y(0) = 0, \quad \dot{y}(0) = 0.
\]
Here
g (
t ) is the Green function for the given differential equation
\[
g(t) = {\cal L}^{-1} \left[ \frac{1}{\lambda^2 + 4} \right] = \frac{1}{2}\, sin (2t)\, H(t) ,
\tag{3.6}
\]
where
H (
t ) is the Heaviside function. So the solution is
\[
y(t) = \left[ \frac{1}{2}\, \sin (2t) - \cos (2t) \right] H(t) + \frac{1}{2}\, sin (2t - 2\pi )\, H(t-\pi )
\tag{3.7}
\]
We plot the the solution (in blue) along with the solution of the inhomogeneous equation y p (t ) in black.
yh[t_] = Sin[2*t]/2 - Cos[2*t];
Plot of the solution (in blue), and y p (t ) in black.
Mathematica code
■
Example 4: Second order differential equation with periodic input
Example 4:
We consider a problem similar to the previous example, but now its forcing function is partially periodic:
\[
\ddot{y} + 4\,y(t) = f( t), \qquad y(0) = -1, \quad \dot{y}(0) = 1,
\tag{4.1}
\]
where
\[
f(t) = \begin{cases}
t, & \ \mbox{ when } \ 0 < t < 1,
\\
\cos \pi (t-1) , & \ \mbox{ when } \ 1 < t < 3,
\\
0, & \ \mbox{ for }\ t> 3 .
\end{cases}
\tag{4.2}
\]
Application of the Laplace transformation yields
\[
\lambda^2 y^L - \dot{y}(0) - \lambda \,y(0) = f^L (\lambda ) ,
\]
where
\[
f^L (\lambda ) = \int_0^{\infty} f(t)\,e^{-\lambda t} {\text d}t = \frac{1}{\lambda^2} + \left[ \frac{\lambda}{\pi^2 + \lambda^2} - \frac{1+ \lambda}{\lambda^2} \right] e^{-\lambda} - \frac{1}{\pi^2 + \lambda^2}\, e^{-3\lambda} .
\tag{4.3}
\]
Integrate[t*Exp[-s*t], {t, 0, 1}] +
Integrate[Cos[Pi*(t - 1)]*Exp[-s*t], {t, 1, 3}]
(E^(-3 s) (-1 + E^(2 s)) s)/(\[Pi]^2 + s^2) + (1 - E^-s (1 + s))/s^2
Solving the algebraic equation for
y L , we obtain
\[
y^L (\lambda ) = {\cal L} \left[ y(t) \right] = \int_0^{\infty} y(t)\,e^{-\lambda t} {\text d} t = \frac{1-\lambda}{\lambda^2 + 4} + \frac{1}{\lambda^2 + 4}\, f^L (\lambda ) .
\tag{4.4}
\]
Taking the inverse Laplace transform, we find the explicit formula for the solution:
\[
y(t) = \left[ \frac{1}{2}\, \sin (2t) - \cos (2t) \right] H(t) + \frac{1}{2}\, \sin (2t) \ast f(t) .
\]
However, explicit evaluation of the convolution in the formula above is not easy. Hence, we use the straightforward approach based on the inverse Laplace transform
\[
y_p (t) = \frac{1}{2}\, \sin (2t) \ast f(t) = {\cal L}^{-1} \left[ \frac{1}{\lambda^2 + 4} \left[ \frac{1}{\lambda^2} + \left( \frac{\lambda}{\pi^2 + \lambda^2} - \frac{1+ \lambda}{\lambda^2} \right) e^{-\lambda} - \frac{1}{\pi^2 + \lambda^2}\, e^{-3\lambda} \right] \right]
\]
We represent this function as the sum of three components:
\[
y_p (t) = g_1 (t) + g_2 (t-1) + g_3 (t-3) ,
\]
where
\begin{align*}
g_1 (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda^2} \,\frac{1}{\lambda^2 + 4} \right] = \left[ \frac{t}{4} - \frac{1}{8}\,\sin 2t \right] H(t) ,
\\
g_2 (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda^2 + 4} \left( \frac{\lambda}{\pi^2 + \lambda^2} - \frac{1+ \lambda}{\lambda^2} \right) \right] = \frac{8 -2\pi +8t -2\pi^2 t + 2\pi^2 \cos 2t -8\,\sin (\pi t) - 4\,\sin 2t + \pi^2 \sin 2t}{8 \left( \pi^2 -4 \right)} \, H(t) ,
\\
g_3 (t) &= {\cal L}^{-1} \left[ \frac{1}{\lambda^2 + 4}\,\frac{1}{\lambda^2 + \pi^2} \right] = \left[ \frac{\pi\,\sin 2t -2\,\sin \pi t}{2\pi \left( \pi^2 -4 \right)} \right] H(t) .
\end{align*}
InverseLaplaceTransform[1/(s^2 + 4)/s^2, s, t]
t/4 - 1/8 Sin[2 t]
InverseLaplaceTransform[
1/(s^2 + 4)*(s/(s^2 + Pi^2) - (1 + s)/s^2), s, t]
(8 - 2 \[Pi]^2 + 8 t - 2 \[Pi]^2 t + 2 \[Pi]^2 Cos[2 t] -
8 Cos[\[Pi] t] - 4 Sin[2 t] + \[Pi]^2 Sin[2 t])/(8 (-4 + \[Pi]^2))
InverseLaplaceTransform[1/(s^2 + 4)/(s^2 + Pi^2), s, t]
(\[Pi] Sin[2 t] - 2 Sin[\[Pi] t])/(2 \[Pi] (-4 + \[Pi]^2))
We plot the the solution (in blue) along with the input function f (t ) in black.
g1[t_] = ( t/4 - 1/8 Sin[2 t])*HeavisideTheta[t];
Plot of the solution (in blue), and f (t ) in black.
Mathematica code
Finally, we plot the first derivative of the solution in blue (it is continuous) along with the second derivative in purple (it is discontinuous at t = 3).
dy[t_] = D[y[t], t];
Plot of the first derivative (in blue), and the second derivative in purple.
Mathematica code
■
Example 5: The case of simple real roots.
Example 5:
\[
y'' + y' - 2\, y = \sin t \left[ H(t-\pi ) - H(t-2\pi ) \right] , \qquad y(0) =1, \quad y'(0) =-1.
\tag{5.1}
\]
Before application of the
Laplace transformation , we rearrange the input function so it will have a suitable form for the shift rule:
\[
f(t) = \sin t \left[ H(t-\pi ) - H(t-2\pi ) \right] = - \sin (t-\pi )\,H(t-\pi ) - \sin (t-2\pi )\,H(t-2\pi )
\tag{5.2}
\]
because sin(
t -π) = -sin(
t ). Now application of the Laplace transform yields
\[
\lambda^2 y^L - y'(0) - \lambda\,y(0) + \lambda\,y^L - y(0) -2\,y^L = f^L (\lambda ) = - \frac{1}{\lambda^2 +1} \left( e^{-\pi\lambda} + e^{-2\pi\lambda} \right) .
\]
From the relation above, we determine the explicit formula for the Laplace transform
y L of the unknown function
y (
t ):
\[
y^L (\lambda ) = \int_0^{\infty} y(t)\, e^{-\lambda\, t}\,{\text d}t = - \frac{1}{\lambda^2 +1}\,\frac{1}{\lambda^2 + \lambda -2} \left( e^{-\pi\lambda} + e^{-2\pi\lambda} \right) + \frac{\lambda}{\lambda^2 + \lambda -2} .
\tag{5.3}
\]
Since the characteristic polynomial has two simple real roots
\( \lambda^2 + \lambda -2 = (\lambda -1)(\lambda +2) , \) we find the inverse Laplace transform of the second term:
\[
y_h (t) = {\cal L}^{-1} \left[ \frac{\lambda}{\lambda^2 + \lambda -2} \right] = \mbox{Res}_{\lambda = 1} \,\frac{\lambda\,e^{\lambda\, t}}{\lambda^2 + \lambda -2} + \mbox{Res}_{\lambda = -2} \,\frac{\lambda\,e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} .
\]
Calculations show that
\begin{align*}
\mbox{Res}_{\lambda = 1} \,\frac{\lambda\,e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} &= \lim_{\lambda\to 1} \,\frac{\lambda\,e^{\lambda\, t}}{(\lambda +2)} = \frac{1}{3}\, e^t , \\
\mbox{Res}_{\lambda = -2} \,\frac{\lambda\,e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} &= \lim_{\lambda\to -2} \,\frac{\lambda\,e^{\lambda\, t}}{(\lambda -1)} = \frac{2}{3}\, e^{-2t} .
\end{align*}
Hence,
\[
y_h (t) = {\cal L}^{-1} \left[ \frac{\lambda}{\lambda^2 + \lambda -2} \right] = \frac{1}{3} \left[ e^t + 2\,e^{-2t} \right] H(t) .
\]
To find the other terms in the solution, we need to introduce an auxiliary function:
\[
g (t) = {\cal L}^{-1} \left[ \frac{1}{\lambda^2 +1}\,\frac{1}{\lambda^2 + \lambda -2} \right] .
\]
The corresponding formula for
g (
t ) is comprised from the following residues:
\begin{align*}
\mbox{Res}_{\lambda = {\bf j}} \,\frac{1}{\lambda^2 +1}\,\frac{e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} &= \lim_{\lambda\to {\bf j}} \,\frac{1}{2\lambda} \,\frac{e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} = \frac{1}{2{\bf j}} \,\frac{e^{{\bf j}\, t}}{({\bf j} -1)({\bf j} +2)} ,
\\
\mbox{Res}_{\lambda = 1} \,\frac{1}{\lambda^2 +1}\,\frac{e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} &= \lim_{\lambda\to 1} \,\frac{1}{\lambda^2 +1}\,\frac{e^{\lambda\, t}}{(\lambda +2)} = \frac{1}{6}\, e^t ,
\\
\mbox{Res}_{\lambda = -2} \,,\frac{1}{\lambda^2 +1}\,\frac{\lambda\,e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} &= \lim_{\lambda\to -2} \,\frac{1}{\lambda^2 +1}\,\frac{e^{\lambda\, t}}{(\lambda -1)} = - \frac{1}{15}\, e^{-2t} .
\end{align*}
Since
\[
\frac{1}{{\bf j}} \,\frac{1}{{\bf j} -1} \,\frac{1}{{\bf j} +2} = - \frac{1}{1 + 3{\bf j}} = - \frac{1 - 3{\bf j}}{1^2 + 3^2} = \frac{1}{10} \left( -1 + 3{\bf j} \right) ,
\]
we add all residues and obtain
\[
g(t) = 2\,\Re\,\mbox{Res}_{\lambda = {\bf j}} \,\frac{1}{\lambda^2 +1}\,\frac{e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} + \mbox{Res}_{\lambda = 1} \,\frac{1}{\lambda^2 +1}\,\frac{e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} + \mbox{Res}_{\lambda = -2} \,,\frac{1}{\lambda^2 +1}\,\frac{\lambda\,e^{\lambda\, t}}{(\lambda -1)(\lambda +2)} ,
\]
which gives
\[
g(t) = \frac{1}{10} \left( -\cos t + 3\,\sin t \right) H(t) + \left( \frac{1}{6}\, e^t - \frac{1}{15}\, e^{-2t} \right) H(t) .
\tag{5.4}
\]
Then the required solution is the sum:
\[
y(t) = y_h (t) -g(t-\pi ) - g(t-2\pi ) .
\tag{4.5}
\]
We check our answer with
Mathematica
InverseLaplaceTransform[s/(s^2 + s - 2), s, t]
1/3 E^(-2 t) (2 + E^(3 t))
InverseLaplaceTransform[1/(s^2 + s - 2)/(s^2 + 1), s, t]
-(1/15) E^(-2 t) + E^t/6 + 1/10 (-Cos[t] - 3 Sin[t])
We plot the solution (in blue) along with the input function f (t ) in black.
g[t_] = ( -(1/15) E^(-2 t) + E^t/6 + 1/10 (-Cos[t] - 3 Sin[t]))*
HeavisideTheta[t];
Plot of the solution (in blue), and f (t ) in black.
Mathematica code
As you see from the graph, the input function
f (
t ) makes almost no influence on the solution because the initial conditions dominate. If we take the initial conditions to be homogeneous, then the solution to the IVP
\[
y'' + y' - 2\, y = \sin t \left[ H(t-\pi ) - H(t-2\pi ) \right] , \qquad y(0) =0, \quad y'(0) =0,
\]
becomes
\[
y_p (t) = -g(t-\pi ) - g(t-2\pi ) .
\]
We plot the particular solution y p (t ) (in blue) along with the input function f (t ) in black.
g[t_] = ( -(1/15) E^(-2 t) + E^t/6 + 1/10 (-Cos[t] - 3 Sin[t]))*
HeavisideTheta[t];
Plot of the particular solution y p (t ) in blue, and f (t ) in black.
Mathematica code
⁎ ✱ ✲ ✳ ✺ ✻ ✼
✽ ❋ ==========================================
Now we consider a similar initial value problem
\[
y'' + 3\,y' + 2\, y = \sin t \left[ H(t-\pi ) - H(t-2\pi ) \right] , \qquad y(0) =1, \quad y'(0) =-1.
\tag{5.6}
\]
Applying the Laplace transformation to the given IVP, we obtain the algebraic equation for
y L , the Laplace transform of the unknown solution
y (
t )
\[
\left( \lambda^2 + 3\lambda + 2 \right) y^L = \lambda +2 + f^L .
\]
Its solution is
\[
y^L (\lambda ) = \frac{\lambda +2}{\lambda^2 + 3\lambda + 2} - \frac{1}{\lambda^2 + 3\lambda + 2}\cdot \frac{1}{\lambda^2 +1} \left( e^{-\pi\lambda} + e^{-2\pi\lambda} \right) + \frac{\lambda}{\lambda^2 + \lambda -2} .
\]
Next, we find two inverse Laplace transforms:
\[
y_h (t) = {\cal L}^{-1} \left[ \frac{\lambda +2}{\lambda^2 + 3\lambda + 2} \right] = e^{-t} H(t) ,
\]
and
\[
g (t) = {\cal L}^{-1} \left[ \frac{1}{\lambda^2 + 3\lambda + 2}\cdot \frac{1}{\lambda^2 +1} \right] = \left[ \frac{1}{6}\, e^t - \frac{1}{15}\,e^{-2t} -\frac{1}{10} \left( \cos t + 3\,\sin t \right) \right] H(t) .
\]
InverseLaplaceTransform[(s + 2)/(s^2 + 3*s + 2), s, t]
E^-t
InverseLaplaceTransform[1/(s^2 + 3*s + 2)/(s^2 + 1), s, t]
-(1/5) E^(-2 t) + E^-t/2 + 1/10 (-3 Cos[t] + Sin[t])
Then the solution of the IVP (4.6) can be expressed through these two functions:
\[
y(t) = e^{-t} H(t) - g(t-\pi ) - g(t- 2\pi ) .
\tag{5.7}
\]
We plot the solution y (t ) to the IVP (5.6) (in blue) along with the input function f (t ) in black.
g[t_] = ( -(1/5) E^(-2 t) + E^-t/2 + 1/10 (-3 Cos[t] + Sin[t]))*
HeavisideTheta[t];
Plot of the solution (5.7) in blue, and f (t ) in black.
Mathematica code
■
Example 6: LC-circuit with intermittent input
Example 6:
We plot the LC-circuit:
cc = Graphics[{Thickness[0.01], Blue,
Line[{{6, 3.5}, {6, 5.5}}]}];
LC-circuit.
Mathematica code
\[
\frac{{\text d}^2 y}{{\text d}t^2} +4\,y = \begin{cases}
4t , & \ 0 < t < 1, \\ 0, & \ \mbox{ otherwise}
, \end{cases} \qquad y(0) =1, \quad y'(0) =-1.
\tag{6.1}
\]
Since the input function can be written as
\[
4t \left[ H(t) - H(t-1) \right] = 4t\,H(t) - 4\left( t-1+1 \right) H(t-1) = 4t\,H(t) - 4\left( t-1 \right) H(t-1) - 4\,H(t-1) ,
\]
we apply the Laplace transform
LaplaceTransform[{y''[t] + 4*y[t] ==
4*t*UnitStep[t] - 4*t*UnitStep[t - 1], y[0] == 1,
y'[0] == -1}, t, pp]
{4 LaplaceTransform[y[t], t, pp] +
pp^2 LaplaceTransform[y[t], t, pp] - pp y[0] -
Derivative[1][y][0] == -4 E^-pp (1/pp^2 + 1/pp) + 4/pp^2, (
y[0] == 1)/pp, (Derivative[1][y][0] == -1)/pp}
So we get the Laplace transform of the unknown solution to be
\[
\left( \lambda^2 +4 \right) y^L = -1 + \lambda + \frac{4}{\lambda^2} - \frac{4}{\lambda^2}\,e^{-\lambda} - \frac{4}{\lambda} \,e^{-\lambda} ,
\]
or
\[
y^L = \frac{\lambda -1}{\lambda^2 +4} + \frac{4}{\lambda^2 \left( \lambda^2 + 4 \right)} - \frac{4}{\lambda^2\left( \lambda^2 + 4 \right)}\,e^{-\lambda} - \frac{4}{\lambda\left( \lambda^2 + 4 \right)} \,e^{-\lambda} .
\]
What is left is to apply the inverse Laplace transform to every term in the right-hand side. Actually, we need to find the values of only three terms:
\[
y_h (t) = {\cal L}^{-1} \left[ \frac{\lambda -1}{\lambda^2 +4} \right] = \left( \cos 2t -\frac{1}{2}\,\sin 2t \right) H(t) ,
\]
\[
g_1 (t) = {\cal L}^{-1} \left[ \frac{4}{\lambda\left( \lambda^2 + 4 \right)} \right] = \left( 1 - \cos 2t \right) H(t) ,
\]
and
\[
g_2 (t) = {\cal L}^{-1} \left[ \frac{4}{\lambda^2 \left( \lambda^2 + 4 \right)} \right] = \left( t - \frac{1}{2}\,\sin 2t \right) H(t) .
\]
InverseLaplaceTransform[(s - 1)/(s^2 + 4), s, t]
1/2 (2 Cos[2 t] - Sin[2 t])
InverseLaplaceTransform[(4)/(s^2 + 4)/s, s, t]
4 (1/4 - 1/4 Cos[2 t])
InverseLaplaceTransform[(4)/(s^2 + 4)/s^2, s, t]
4 (t/4 - 1/8 Sin[2 t])
This allows us to determine the solution explicitly:
\[
y(t) = y_h (t) + g_2 (t) - g_2 (t-1) - g_1 (t-1) .
\tag{6.2}
\]
We plot the solution y (t ) to the IVP (6.1) (in blue) along with the input function f (t ) in black.
yh[t_] = 1/2 (2 Cos[2 t] - Sin[2 t])*HeavisideTheta[t];
Plot of the solution (6.2) in blue, and f (t ) in black.
Mathematica code
We plot the second derivative of the solution y (t ) to the IVP (6.1) (in blue) along with the input function f (t ) in black.
Plot[{Piecewise[{{t, 0 < t < 1}}] - 4*y[t],
Piecewise[{{t, 0 < t < 1}}]}, {t, 0, 3},
PlotStyle -> {{Thickness[0.015], Blue}, {Thickness[0.01], Black}},
PlotRange -> {-5, 2}, AspectRatio -> 1]
Plot of the second derivative of the solution (8.2) in blue, and f (t ) in black.
Mathematica code
■
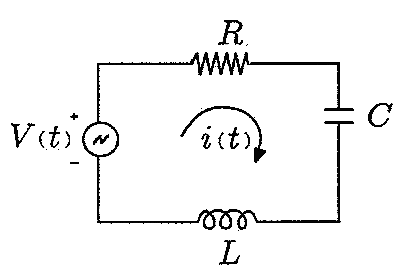
Example 7: RLC electric circuit
Example 7: resistor , an inductor ,
and a capacitor
are connected in series with a voltage supply, the circuit
obtained is called a series RLC circuit.
The differential equation governing the charge
q (
t ) on the capacitor in the RLC circuit is
\[
L\,\ddot{q} + R\,\dot{q} + \frac{1}{C}\,q (t) = \dot{E}(t), \qquad \ddot{q} = \frac{{\text d}^2 q}{{\text d}t^2} , \quad \dot{q} = \frac{{\text d}q}{{\text d}t} = i(t) .
\tag{7.1}
\]
This differential equation is supplemented with the initial conditions:
\[
q(0) = q_0 , \qquad \dot{q}(0) = i(0) = i_0 .
\tag{7.2}
\]
We assume that the derivative of the electromotive force is the rectangular pulse of magnitude one (for simplicity):
\[
\dot{E}(t) = H(t-2) - H(t-5) = W(t; 2,5) .
\]
Application of the Laplace transformation to the differential equation (7.1) yields
\[
\left( L \lambda^2 + R\lambda + 1/C \right) q^L = L\,i(0) + \left( L\lambda + R \right) q(0) + e^L (\lambda ) ,
\]
where
\[
q^L = {\cal L} \left[ q(t) \right] = \int_0^{\infty} e^{-\lambda t} q(t) \,{\text d}t, \qquad e^L = \int_0^{\infty} e^{-\lambda t} \dot{E}(t) \,{\text d}t = \frac{1}{\lambda} \left( e^{-2\lambda} - e^{-5\lambda} \right) .
\]
Then the Laplace transform of
q (
t ) is the sum of two terms
\[
q^L = {\cal L} \left[ q(t) \right] = \frac{L\,i(0) + \left( L\lambda + R \right) q(0) }{L \lambda^2 + R\lambda + S} + \frac{1}{L \lambda^2 + R\lambda + S} \cdot \frac{1}{\lambda} \left( e^{-2\lambda} - e^{-5\lambda} \right) ,
\]
where
S = 1/
C is the elastance.
The inverse Laplace transform of the first term is the solution of the homogeneous differential equation subject to the given initial conditions
\[
L\,\ddot{q} + R\,\dot{q} + \frac{1}{C}\,q (t) = 0, \qquad q(0) = q_0 , \quad \dot{q}(0) = i(0) = i_0 .
\tag{7.3}
\]
We denote its solution as
\[
q_h (t) = {\cal L}^{-1} \left[ \frac{L\,i(0) + \left( L\lambda + R \right) q(0) }{L \lambda^2 + R\lambda + S} \right]
\tag{7.4}
\]
On the other hand, the inverse Laplace transform of the second term is the particular solution of the inhomogeneous equation
\[
L\,\ddot{q} + R\,\dot{q} + \frac{1}{C}\,q (t) = E(t), \qquad q(0) =0, \quad \dot{q} (0) = 0.
\tag{7.5}
\]
Its solution is
\[
y_p (t) = {\cal L}^{-1} \left[ \frac{1}{L \lambda^2 + R\lambda + S} \cdot \frac{1}{\lambda} \left( e^{-2\lambda} - e^{-5\lambda} \right) \right] = p(t-2) - p(t-5) ,
\tag{7.6}
\]
where
\[
p(t) = {\cal L}^{-1} \left[ \frac{1}{L \lambda^2 + R\lambda + S} \cdot \frac{1}{\lambda} \right] H(t) .
\tag{7.7}
\]
We find the explicit expressions for solutions (7.4) and (7.7) under the following conditions:
\[
L = 5\,\mbox{H}, \quad R = 20\,\Omega , \quad C= 0.005\,\mbox{F} \quad\mbox{or} \quad S = 1/C = 200\,\mbox{S}, \qquad q(0) = 1\,\mbox{C}, \quad i(0) = -1\,\mbox{A}.
\]
Then these functions become
\[
y_h (t) = {\cal L}^{-1} \left[ \frac{15+5\lambda}{5 \lambda^2 + 20\lambda + 200} \right] = {\cal L}^{-1} \left[ \frac{3+\lambda}{\lambda^2 + 4\lambda + 400} \right] = e^{-2t} \left( \cos 6t + \frac{1}{6}\,\sin 6t \right) H(t) ;
\]
and
\[
p(t) = {\cal L}^{-1} \left[ \frac{1}{5 \lambda^2 + 20\lambda + 200}\cdot \frac{1}{\lambda} \right] = \left[ \frac{3}{40} - \frac{3}{40}\,e^{-2t} \cos 6t + \frac{17}{120}\,e^{-2t} \sin 6t \right] H(t) .
\]
InverseLaplaceTransform[(15 + 5*s)/(5*s^2 + 20*s + 200)/s, s, t];
1/120 E^(-2 t) (9 E^(2 t) - 9 Cos[6 t] + 17 Sin[6 t])
We plot the particular solution (7.6) (in blue) along with the input function in black.
p[t_] = 1/120 E^(-2 t) (9 E^(2 t) - 9 Cos[6 t] + 17 Sin[6 t])*
HeavisideTheta[t];
Plot of the particular solution (7.6) in blue, and the input function in black.
Mathematica code
■
Example 8: The case of double real roots.
Example 8:
\[
y'' -6\,y' + 9\, y = H(t-1) - H(t-3), \qquad y(0) =1, \quad y'(0) =-1.
\tag{8.1}
\]
Application of the Laplace transform yields
\[
\left( \lambda^2 -6\lambda + 9 \right) y^L = f^L + \lambda -7 ,
\]
where
\[
f^L (\lambda ) = {\cal L} \left[ H(t-1) - H(t-3) \right] = \frac{1}{\lambda} \left( e^{-\lambda} - e^{-3\lambda} \right)
\]
is the Laplace transform of the input function. Solving for the Laplace transform of the unknown function, we obtain
\[
y^L (\lambda ) = \frac{1}{\lambda \left( \lambda^2 -6\, \lambda + 9 \right)} \left( e^{-\lambda} - e^{-3\lambda} \right) + \frac{\lambda -7}{\lambda^2 -6\, \lambda + 9} .
\]
The inverse Laplace transform of the last term is
\[
y_h = {\cal L}^{-1} \left[ \frac{\lambda -7}{(\lambda -3)^2} \right] =
\lim_{\lambda \to 3} \,\frac{\text d}{{\text d}\lambda}\,\left( \lambda -7 \right) e^{\lambda\, t} .
\]
This function,
\[
y_h = \left[ -4t + 1 \right] e^{3t}\,H(t)
\]
is a the solution of the homogeneous differential equation
\( y'' -6\, y' +9\,y =0 \) and satisfies the given initial conditions:
y (0) = 1,
y' (0) = -1.
To find the solution
\[
y_p (t) = {\cal L}^{-1} \left[ \frac{1}{(\lambda -3)^2}\,f^L \right] = {\cal L}^{-1} \left[ \frac{1}{(\lambda -3)^2}\,\frac{1}{\lambda} \left( e^{-\lambda} - e^{-3\lambda} \right) \right]
\]
of the nonhomogeneous equation
\( y'' -6\, y' + 9\, y = H(t-1) - H(t-3), \) we need to determine first the function
\[
g(t) = {\cal L}^{-1} \left[ \frac{1}{\lambda \left( \lambda -3 \right)^2} \right] .
\]
Then the solution of the nonhomogeneous equation that satisfies the homogeneous initial conditions will be expressed through this function:
\[
y_p (t) = g(t-1) - g(t-3) .
\]
So the required solution will be sum of
y p and
y h :
\[
y(t) = y_p (t) + y_h = g(t-1) - g(t-3) + y_h .
\]
Using the residue theorem, we get
\[
g(t) = \mbox{Res}_{\lambda =0} \frac{e^{\lambda t}}{\lambda \left( \lambda -3 \right)^2} + \mbox{Res}_{\lambda =3} \frac{e^{\lambda t}}{\lambda \left( \lambda -3 \right)^2} .
\]
We calculate separately each of the above residues
\begin{align*}
\mbox{Res}_{\lambda =0} \frac{e^{\lambda t}}{\lambda \left( \lambda -3 \right)^2} &= \lim_{\lambda \to 0} \, \frac{e^{\lambda t}}{\left( \lambda -3 \right)^2} = \frac{1}{9} ,
\\
\mbox{Res}_{\lambda =3} \frac{e^{\lambda t}}{\lambda \left( \lambda -3 \right)^2} &= \lim_{\lambda \to 3} \,\frac{\text d}{{\text d}\lambda} \,\frac{e^{\lambda t}}{ \lambda} = \frac{t}{3}\,e^{3t} -\frac{1}{9}\,e^{3t} .
\end{align*}
This allows us to determine
g (
t ) to be
\[
g(t) = \left[ \frac{1}{9} + \left( \frac{t}{3} -\frac{1}{9} \right) e^{3t} \right] H(t) .
\tag{8.2}
\]
Note that the function
g (
t ) satisfies the homogeneous initial conditions:
g (0) = 0 and
g '(0) = 0.
We check our calculations with Mathematica :
InverseLaplaceTransform[(s - 7)/(s^2 - 6*s + 9), s, t]
-E^(3 t) (-1 + 4 t)
InverseLaplaceTransform[(1)/(s^2 - 6*s + 9)/s, s, t]
1/9 (1 - E^(3 t) + 3 E^(3 t) t)
⁎ ✱ ✲ ✳ ✺ ✻ ✼
✽ ❋ =================================
Now we consider a similar problem
\[
y'' +6\,y' + 9\, y = H(t-1) - H(t-3), \qquad y(0) =1, \quad y'(0) =-1.
\tag{8.3}
\]
Application of the Laplace transform yields
\[
\left( \lambda^2 +6\lambda + 9 \right) y^L = f^L + \lambda +5 ,
\]
■
Example 9: The case of complex roots.
Example 9:
\[
y'' -4\,y' + 5\,y = \cos t\,H(t-\pi ), \qquad y(0) =1, \quad y'(0) =-1.
\tag{9.1}
\]
Representing the input function in the shift form
\[
\cos t\,H(t-\pi ) = -\cos \left( t - \pi \right) H \left( t - \pi \right) ,
\]
we apply the Laplace transform
\[
\lambda^2 y^L - y'(0) - \lambda\,y(0) - 4\,y^L + 4\,y(0) + 5\,y^L = f^L (\lambda ) = - \frac{\lambda}{\lambda^2 +1}\, e^{-\pi\lambda} .
\]
This allows us to find the explicit formula for the Laplace transform of the unknown function
\[
y^L (\lambda ) = \frac{1}{\lambda^2 - 4\,\lambda + 5} \,f^L (\lambda ) + \frac{\lambda -5}{\lambda^2 - 4\,\lambda + 5} .
\tag{9.2}
\]
So we represent it as the sum
\[
y^L (\lambda ) = y^L (\lambda ) + y_h (\lambda ) ,
\]
where
\[
y^L_p (\lambda ) =\frac{f^L}{\lambda^2 - 4\,\lambda + 5} = -\frac{1}{\lambda^2 - 4\,\lambda + 5} \,\frac{\lambda}{\lambda^2 +1}\, e^{-\pi\lambda} , \qquad y_h (\lambda ) = \frac{\lambda -5}{\lambda^2 - 4\,\lambda + 5} .
\]
Since the characteristic polynomial λ² - 4 λ + 5 has two complex conjugate roots λ = 2 ±
j , with
j ² = -1, we have
\[
y_h = 2\,\Re\,\mbox{Res}_{\lambda = 2 +{\bf j}} \,\frac{\lambda -5}{\lambda^2 - 4\,\lambda + 5}\, e^{\lambda\,t} = 2\,\Re\,\lim_{\lambda\to 2+{\bf j}}\frac{\lambda -5}{2\lambda -4 }\, e^{\lambda\,t} = 2\,\Re\,\frac{{\bf j}-3}{2{\bf j}}\, e^{2t} e^{{\bf j}t}
\]
So
\[
y_h = \left( \cos t - 3\,\sin t \right) e^{2t} \,H(t) .
\]
This function satisfies the given initial conditions:
y h (0) = 1 and
y' h (0) = -1. Another function
y p (
t ) is a shifted version of another function:
\[
y_p = -g\left( t - \pi \right) ,
\]
where
\[
g(t) = {\cal L}^{-1} \left[ \frac{1}{\lambda^2 - 4\,\lambda + 5} \,\frac{\lambda}{\lambda^2 +1} \right] = 2\,\Re\, \left( \mbox{Res}_{\lambda = {\bf j}} + \mbox{Res}_{\lambda = {2+\bf j}} \right) \frac{1}{\lambda^2 - 4\,\lambda + 5} \,\frac{\lambda}{\lambda^2 +1} \,e^{\lambda t} .
\]
We evaluate each residue separately
\begin{align*}
\mbox{Res}_{\lambda = {\bf j}} \, \frac{1}{\lambda^2 - 4\,\lambda + 5} \,\frac{\lambda}{\lambda^2 +1} \,e^{\lambda t} &= \lim_{\lambda\to {\bf j}} \, \frac{1}{\lambda^2 - 4\,\lambda + 5} \,\frac{\lambda}{2\lambda} \,e^{\lambda t} = \frac{1}{2}\,\frac{1}{8} \left( 1 + {\bf j} \right) e^{{\bf j}t} ,
\\
\mbox{Res}_{\lambda = {2+\bf j}} \, \frac{1}{\lambda^2 - 4\,\lambda + 5} \,\frac{\lambda}{\lambda^2 +1} \,e^{\lambda t} &= \lim_{\lambda\to 2+{\bf j}} \,\frac{1}{2\lambda -4}\,\frac{\lambda}{\lambda^2 +1} \,e^{\lambda t} = - \frac{1}{16} \left( 1 + 3 {\bf j} \right) e^{2t} e^{{\bf j}t} .
\end{align*}
Taking the real part, we obtain
\[
g(t) = \frac{1}{8} \left[ \left( \cos t - \sin t \right) + \left( -\cos t + 3\, \sin t \right) e^{2t} \right] H(t) .
\]
Then
\[
y(t) = y_p (t) + y_h (t) = -g(t-\pi ) + y_h (t) .
\]
⁎ ✱ ✲ ✳ ✺ ✻ ✼
✽ ❋ =================================
Now we consider a similar problem
\[
y'' +4\,y' + 5\,y = \cos t\,H(t-\pi ), \qquad y(0) =1, \quad y'(0) =-1.
\tag{9.3}
\]
■
Mathematica solves differential equations
We demonstrate usefulness of
Mathematica in the following example devoted to solve the initial value problem
\[
\ddot{y} + 5\,\dot{y} + 6\,y = H(t-2), \qquad y(0) = 1, \quad \dot{y}(0) = -1.
\]
Example 10: Mathematica helps to utilize the Laplace transformation.
Example 10:
LaplaceTransform[
Out[15]= 6 LaplaceTransform[y[t], t, lambda] +
% /. {y[0] -> -1, y'[0] -> 5}
Out[16]= -5 + lambda + 6 LaplaceTransform[y[t], t, lambda] +
So the Laplace transform of the unknown function is
\[
y^L (\lambda ) = \frac{\lambda +5}{\lambda^2 + 5\lambda +6} + \frac{1}{\lambda^2 + 5\lambda +6}\,\frac{1}{\lambda} \, e^{-2\lambda} .
\tag{10.1}
\]
InverseLaplaceTransform[%, lambda, t]
Out[18]= {{y[t] -> -(1/6)
E^(-3 t) (18 -
Plot[HeavisideTheta[t - 2], {t, 0, 6}] (* plot the unit function with discontinuities *)
L[t_, y_] := y''[t] - 5 y'[t] + 6 y[t] + HeavisideTheta[t - 1]
Out[15]= E^-s/s + 6 LaplaceTransform[y[t], t, s] +
% /. {y[0] -> -1, y'[0] -> 5}
Out[16]= -5 + E^-s/s + s + 6 LaplaceTransform[y[t], t, s] +
Solve[%, LaplaceTransform[y[t], t, s]]
Out[17]= {{LaplaceTransform[y[t], t, s] -> -((
InverseLaplaceTransform[%, s, t]
Out[18]= {{y[t] -> -(1/(
6 E^6))(-6 E^(6 + 2 t) (-8 + 7 E^t) -
Since the inverse Laplace transforms of ratios in Eq.(9.1) are
\begin{align*}
y_h (t) &= {\cal L}^{-1} \left[ \frac{\lambda +5}{\lambda^2 + 5\lambda +6} \right] = \left( 3\, e^{-2t} - 2\,e^{-3t} \right) H(t) ,
\\
g(t) &= {\cal L}^{-1} \left[ \frac{1}{\left( \lambda^2 + 5\lambda +6 \right) \lambda} \right] = \frac{1}{6} \left( 1 - 3\,e^{-2t} + 2\, e^{-3t} \right) H(t) ,
\end{align*}
InverseLaplaceTransform[(s+5)/(s^2 + 5*s + 6), s, t]
E^(-3 t) (-2 + 3 E^t)
InverseLaplaceTransform[(1)/(s^2 + 5*s + 6)/s, s, t]
1/6 E^(-3 t) (-1 + E^t)^2 (2 + E^t)
we get the solution
\[
y(t) = y_h (t) + g(t-2) .
\tag{9.2}
\]
v[t_] = y[t] /. %
We plot the solution y (t ) to the given initial value problem (in blue) along with the input function H (t−2 ) in black.
g[t_] = (1/6 E^(-3 t) (-1 + E^t)^2 (2 + E^t))*HeavisideTheta[t];
Plot of the solution (9.2) in blue, and H (t−2 ) in black.
Mathematica code
■