Numerical Methods and Applications
This tutorial contains many Mathematica scripts. You, as the user, are free to use all codes for your needs, and have the right to distribute this tutorial and refer to this tutorial as long as this tutorial is accredited appropriately. Any comments and/or contributions for this tutorial are welcome; you can send your remarks to <Vladimir_Dobrushkin@brown.edu>
Return to computing page for the second course APMA0330
Return to Mathematica tutorial page for the first course
Return to Mathematica tutorial page for the second course
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Contents
Part III Numerical Methods and Applications
a) Euler methods
b) Polynomial approximations
c) Runge-Kutta methods
d) Multistep methods
4) Numerov's method
Applications
3.0. Introduction
It would be very nice if discrete models provide calculated solutions to differential (ordinary and partial) equations exactly, but of course they do not. In fact in general they could not, even in principle, since the solution depends on an infinite amount of initial data. Instead, the best we can hope for is that the errors introduced by discretization will be small when those initial data are resonably well-behaved.
In this chapter, we discuss some simple numerical method applicable to first order ordinary differential equations in normal form subject to the prescribed initial condition:
We always assume that the slope function \( f(x,y) \) is smooth enough so that the given initial value problem has a unique solutions and the slope function is differentiable so that all formulas make sense. Since it is an introductory, we do not discuss discretization errors in great detail---it is subject of another course. A user should be aware that the magnitude of global errors may depend on the behavior of local errors in ways that ordinary analysis of discretization and rounding errors cannot predict. The most part of this chapter is devoted to some finite difference methods that proved their robastness and usefullness, and can guide a user how numerical methods work. Also, presented codes have limited applications because we mostly deal with uniform truncation meshes/grids that practically are not efficient. We do not discuss adaptive Runge--Kutta--Fehlberg algorithms of high order that are used now in most applications, as well as spline methods. Instead, we present some series approximations as an introduction to application of recurrences in practical life.
The finite diference approximations have a more complecated "physics" than the equations they are designed to simulate. In general, finite recurrences usually have more propertities than their continuous anologous counterparts. However, this arony is no paradox for finite differences are used not because the numbers they generate have simple properties, but because those numbers are simple to compute.
3.1. Numerical Solution using DSolve and NDSolve
A complete analysis of a differential equation is almost impossible without utilizing computers and corresponding graphical presentations. We are not going to pursue a complete analysis of numerical methods, which usually requires:
an understanding of computational tools;
an understanding of the problem to be solved;
construction of an algorithm which will solve the given mathematical problem.
In this chapter, we concentrate our attention on presenting some simple numerical algorithms for finding solutions of the initial value problems for the first order differential equations in the normal form:
assuming that the given problem has a unique solution.
A general approach to find numerically solutions of the initial value problems and then plot them using Mathematica's capability is as follows:
Plot[y[x] /. a, {x,0,3}]
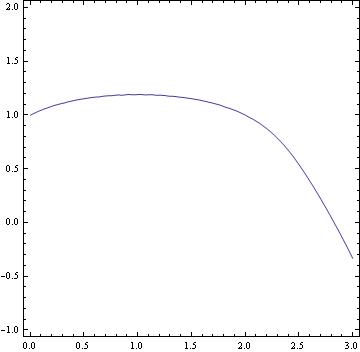
The above script was used to solve (and then plot) the non-linear differential equstion \( y' = (1-x)/(1+y^5) \) subject to the initial condition \( y(0) =1.\) To see a numerical value at, say x=3.0, we type:
ContourPlot[psi[x, y] == 0, {x, 0, 2}, {y, -1, 3}, ContourLabels->True, ColorFunction->Hue]

Example 1.3.1:
?FresnelS
FresnelS[z] gives the Fresnel integral S(z). >>
This indicates that y(6.5) approximately equal to 0.639918. We can improve accuracy by choosing the option PrecisionGoal
There are two main approaches to find a numerical value for the solution to the initial value problem y' = f(x,y), y( x0 )= y0 when its solution can be obtained using either DSolve (for analytical solution, if it is possible) or NDSolve (for numerical solution) command. The first one is based on definition of the slope function f(x,y) as an expression. The second one (which is recommended) is to define the slope as a function. To see how it works, let us consider an example.
Example 1.3.2: Consider the slope function f(x,y) = 1/(3*x - 2*y + 1). Then we find a numerical value treating f(x,y) as an expression.
Now we use the function DSolve to find explicit solution:
Solve::ifun: Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. >>
We present two other options to find a numerical value of a solution to the initial value problem using NDSolve.
y[x] /. sol /. x -> 3
3.2. Euler's Methods
I. Euler Method
In 1768, Leonhard Euler (St. Petersburg, Russia) introduced a numerical method that is now called the Euler method or the tangent line method for solving numerically the initial value problem:
\[ y' = f(x,y), \qquad y(x_0 ) = y_0 , \]
where f(x,y) is the given slope (rate) functions, and \( (x_0 , y_0 ) \) is a prescribed point on the plane. Euler's method or rule is a very basic algorithm that could be used to generate a
numerical solution to a first order initial value problem. The solution that it produces will be returned
to the user in the form of a list of points. The user can then do whatever one likes with this output, such
as create a graph, or utilize the point estimates for other purposes.
y_{n+1} = y_n + (x_{n+1} - x_n ) f( x_n , y_n ) \qquad \mbox{or} \qquad y_{n+1} = y_n + h f_n , \end{equation}
where the following notations are used: \( h=x_{n+1} - x_n \) , \( f_n = f( x_n , y_n ) \) , and \( y_n \) denotes the approximate value of the actual solution \( y=\phi (x) \) at the point \( x_n \) (\( n=1,2,\ldots \) ).
There are several ways to implement the Euler numerical method for solving initial value problems. We demonstrate its implementation in a series of codes. To start, define the initial point and then the slope function:
Clear[x0,y0,x,y,f]
{x0, y0} = {0, 1}
f[x_, y_] = x^2 + y^2 (* slope function f(x,y) = x^2 + y^2 was chosen for concreteness *)
Next, define the step size:
Plot with some options: Another way is to make a loop. Clear[y] Explanation. First of all, it is always important to clear all previous
assignment to all the variables that we are going to use, so we have: Clear[y] The basic structure of the loop is: First, we start with output of our program, which is, perhaps, the most important
part of our program design. You'll notice that in the program
description, we are told that the "solution that it
produces will be returned to the user in the form of a list of
points. The user can then do whatever one likes with this output, such
as create a graph, or utilize the point estimates for other purposes. Next, we must decide upon the information that must be passed to the
program for it to be able to achieve this. In programming jargon,
these values are often referred to as parameters. So what parameters
would an Euler program need to know in order to start solving the
problem numerically? Quite a few should come to mind: The slope function f(x, y) To code these parameters into the program, we need to decide on actual
variable names for each of them. Let's choose variable names as
follows: f, for the slope function f(x, y) There are many ways to achieve this goal. However, it is natural to
have the new subroutine that looks similar to build-in Mathematica's commands. So we want our program might look something like this: In order to use Euler's method to generate a numerical solution to an
initial value problem of the form: We have to decide upon what interval, starting at the initial point x0, we
desire to find the solution. We chop this interval into small subdivisions of length h, called step size. Then, using the initial condition \( (x_0,y_0) \) as our
starting point, we generate the rest of the solution by using the
iterative formulas: to find the coordinates of the points in our numerical solution. The algorithm is
terminated when the right end of the
desired interval has been reached. If you would like a built-in Euler’s method, unluckily there is none. However, we can define it
ourself. Simply copy the following command line by line: Now we have our euler function: euler[f(x,y), {x,x0,x1},{y,y0},steps]
or
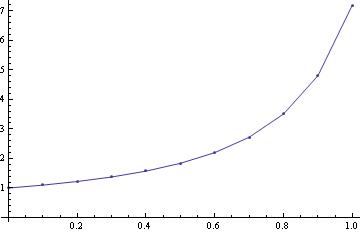
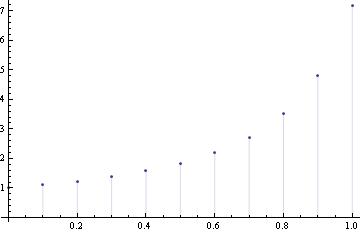
y[0]=1; f[x_,y_]=x^2 +y^2 ;
Do[y[n + 1] = y[n] + h f[1+.01 n, y[n]], {n, 0, 99}]
y[10]
Do[some expression with n, {n, starting number, end number}]
or with option increment, denoted by k:
Do[some expression with n, {n, starting number, end number, k}]
The function of this Do loop is to repeat the expression, with n taking values from “starting
number” to “ending number,” and therefore repeat the expression (1+ (ending number) - (starting
number)) many times. For our example, we want to iterate 10 steps, so n will go from 0, 1, 2, ...,
until 9, which is 10 steps in total. There is just one technical issue: we must have n as an
integer. Therefore we let y[n] denote the actual value of y(x) when x=n*h. This way everything is an
integer, and we have our nice do loop.
Finally put y[10] , which is actualy y(2), then shift+return, and we have our nice answer.
The initial x-value, x0
The initial y-value, y0
The final x-value,
The number of subdivisions to be used when chopping the solution
interval into individual jumps or the step size.
x0, for the initial x-value, x0
y0, for the initial y-value, y0
xn, for the final x-value
Steps, for the number of subdivisions
h, for step size
Block[{ xold = x0, yold = y0, sollist = {{x0, y0}}, h },
h = N[(xn - x0) /Steps]; (* or n = (xn - x0) /Steps//N; *)
Do[ xnew = xold + h;
ynew = yold + h * (f /. {x -> xold, y -> yold});
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew,
{Steps}
];
Return[sollist]
]
Then this script will solve the differential equation y’=f(x,y), subject to the initial condition y(x0)=y0, and generate all values
between x0 and x1. The number of steps for the Euler’s method is specified with steps.
To solve the same problem as above, we simply need to input:
Another example:
1.72102}, {0.6, 1.94312}, {0.7, 2.19743}, {0.8, 2.48718}, {0.9, 2.8159}, {1., 3.18748}}
We can plot the output as follows

Or we can plot it as
1.72102}, {0.6, 1.94312}, {0.7, 2.19743}, {0.8, 2.48718}, {0.9,
2.8159}, {1., 3.18748}}

The following code, which uses a slightly different programming
paradigm, implements Euler's method for a system of differential equations:
Module[{t, Y, h = (b - a)/Steps//N, i},
t[0] = a; Y[0] = Y0;
Do[
t[i] = a + i h;
Y[i] = Y[i - 1] + h F[t[i - 1], Y[i - 1]],
{i, 1, n}
];
Table[{t[i], Y[i]}, {i, 0, n}]
]
And the usage message is:
euler::usage = "euler[F, t0, Y0, b, n] gives the numerical solution
to {Y' == F[t, Y], Y[t0] == Y0} over the interval\n
[t0, b] by the n-step Euler's method. The result
is in the form of a table of {t, Y} pairs."
Note that this function uses an exact increment h rather than converting
it explicitly to numeric form using N. Of course you can readily hange
that or accomplish the corresponding thing by giving an approximate
number for one of the endpoints.
Next we plot the points by joining them with a curve:

Another way without writing a subroutine:
x0 = 0;
y0 = 1;
xend = 1.1;
steps = 5;
h = (xend - x0)/steps // N;
x = x0;
y = y0;
eulerlist = {{x, y}};
For[i = 1, i <= steps, y = f[x, y]*h + y;
x = x + h;
eulerlist = Append[eulerlist, {x, y}]; i++]
Print[eulerlist]
The results can also be visualized by connecting the points:
s = NDSolve[{u'[t] == f[x, u[t]], u[0] == 1}, u[t], {t, 0, 1.1}];
b = Plot[Evaluate[u[x] /. s], {x, 0, 1.1}, PlotStyle -> RGBColor[1, 0, 0]];
Show[a,b]

Next, we demonstrate application of Function command:
Module[{h = (t1 - t0)/n // N, tt, yy},
tt[0] = t0; yy[0] = y0;
tt[k_ /; 0 < k < n] := tt[k] = tt[k - 1] + h;
yy[k_ /; 0 < k < n] :=
yy[k] = yy[k - 1] + h f[tt[k - 1], yy[k - 1]];
Table[{tt[k], yy[k]}, {k, 0, n - 1}]
];
Plot[Interpolation[ty][t], {t, 1, 2}]

Here is another steamline of the Euler method (based on Mathematica function).
f[x_, y_] := y^2 - 3*x^2
x[1] = 0; y[1] = 1;
h = 0.1;
Do[ { x[i+1] = x[i]+h,
y[i+1] = y[i] +h*f[x[i],y[i]] } , {i,1,20} ]
Now we can plot our results, making sure we only refer to values of x and y that we have defined: Now we are going to repeat the problem, but using Mathematica lists format instead. The idea is still the same---we set a new x value, compute the corresponding y value, and save the two quantities in two lists. In particular, in a list we are simply storing values; In previously presented code, we were actually storing rules, which are more complicated to store and evaluate. We start out with just one value in each list (the initial conditions). Then we use the Append command to add our next pair of values to the list.
pairs = Table[{x[i], y[i]}, {i, 1, 11}]
ListPlot[pairs, Joined -> True]
x = {0.0 };
y = {2.0 };
h = 0.1;
Do [ { x = Append[x,x[[i]]+h],
y = Append[y,y[[i]]+h*f[x[[i]],y[[i]] ] ],
} , {i,1,20} ]
Now we can plot our results:
pairs = Table[ {x[[i]], y[[i]] }, {i,1,21} ]
ListPlot [ pairs, Joined -> True ]
h = 0.1
K = IntegerPart[1.2/h] (* if the value at x=1.2 is needed *)
y[0] = 1 (* initial condition *)
Euler method:
y[K]
Euler's method is first-order accurate, so that errors occur one order
higher starting at powers of \( h^2 . \)
Euler's method is implemented in NDSolve as ExplicitEuler:
Method -> "ExplicitEuler", "StartingStepSize" -> 1/10]
Euler's method is first-order accurate, so that errors occur one order
higher starting at powers of \( h^2 . \)
Euler's method is implemented in NDSolve as ExplicitEuler:
Method -> "ExplicitEuler", "StartingStepSize" -> 1/10]
II. Backward Euler Method
Backward Euler formula:
where h is the step size. Consider the following initial value problem:
Here is the Mathematica code that solve this problem:
h = 0.1; (* step size *)
t[0] = 0.; (* starting vaue of the independent value *)
M = Round[0.5/h]; (* number of points to reach the final destination, in our case it is 0.5 *)
toler = h; (* define the tolerance *)
Do[
t[n + 1] = t[n] + h;
eqn = (z == y[n] + h (z^3 - 3 t[n + 1]) );
ans = z /. NSolve[eqn, z, Reals];
indlist = {};
toler = h;
While[ Length[indlist] == 0,
toler = toler*2.;
indlist = Flatten[Position[Map[(Abs[y[n] - #] < toler) &, ans], True]];
];
ind = indlist[[1]];
y[n + 1] = ans[[ind]];
, {n, 0, M}]
Then we plot solution:
y[M]
t[M]

NSolve has to spend time to compute all roots to the equation (which can be computationally expensive). FindRoot does a pretty fast search looking for only a single root, so it is quick for complex equations.
If you care about all possible roots, or if you have no clue where the roots of the equation may be, FindRoot is a terrible choice. If you only care about a single root and have a rough idea of where it might be, though, FindRoot will find it quickly.
III.Trapezoid Rule
The concept of the Trapezoidal Rule in numerical methods is similar to the trapezoidal rule of Riemann sums. The Trapezoid Rule is generally more accurate than the above Euler approximations, and it calculates approximations by taking the sum of the function of the current and next term and multiplying it by half the value of h. Therefore the Mathematica syntax will be as follows:
IV.Heun's Formula / Improved Euler Method
The Improved Euler’s method, also known as the Heun formula or the average slope method, gives a more accurate approximation than the trapezoid rule and gives an explicit formula for computing y(n+1) in terms of the values of x. The basic idea is to correct
some error of the original Euler's method. The syntax of the Improved Euler’s method is similar to that of the trapezoid rule, but the y value of the function in terms of y(n+1) consists of the sum of the y value and the product of h and the function in terms of x(n) and y(n).
Improved Euler formula or the
average slope method or it is commonly referred to as the Heun method
(although discovered by C. Runge):
Clear[y]
f[x_, y_] := x^2 + y^2
y[0] = 1;
h:=0.1;
Do[k1 = h f[h n, y[n]];
k2 = h f[h (n + 1), y[n] + k1];
y[n + 1] = y[n] + .5 (k1 + k2),
{n, 0, 9}]
y[10]
The main difference here is that instead of using y[n+1]=y[n]+h*f(x[n],y[n]), we use
Block[{ xold = x0,
yold = y0,
sollist = {{x0, y0}}, h
},
h = N[(xn - x0) / steps];
Do[ xnew = xold + h;
k1 = h * (f /. {x -> xold, y -> yold});
k2 = h * (f /. {x -> xold + h, y -> yold + k1});
ynew = yold + .5 * (k1 + k2);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew,
{steps}
];
Return[sollist]
]
Instead of calculating intermediate values k1 and k2 , one can define ynew directly:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
ynew =
yold + (h/2)*((fold) + f /. {x -> xold + h, y -> yold + h*fold});
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
The function heun is basically used in the same way as the function euler. Then to solve the
above problem, do the following:
Then read the answer off the table.
Another option:
h = 0.1
K = IntegerPart[1.2/h] (* if the value at x=1.2 needed *)
y[0] = 1 (* initial condition *)
Then implement Heun's rule:
y[n] + (h/2)*f[n*h, y[n]] + (h/2)*
f[h*(n + 1), y[n] + h*f[n*h, y[n]]], {n, 0, K}]
y[K]
Example 1.3.1:
Solve the IVP: \( y'= 1/(3x-2y+1), y(0)=0 \)First, we find its solution using Mathematica's command DSolve:
DSolve[{y'[x] == f[x, y[x]], y[0] == 0}, y[x], x]
To evaluate the exact solution at x=1.0, we type
y[x] /. a /. x -> 1.0
Then we use Heun's numerical method with step size h=0.1:
Do[k1 = h f[n*h, y[n]]; k2 = h f[h*(n + 1), y[n] + k1];
y[n + 1] = y[n] + 0.5*(k1 + k2), {n, 0, 9}]
y[10]
Now we demonstrate the use of while command:
i = 1
h=0.1;
Array[x, Nsteps];
Array[y, Nsteps];
While[i < Nsteps+1, x[i] = x[i - 1] + h; i++];
k=1
While[k < Nsteps,
y[k] = y[k - 1] + (h/2)*
Function[{u, v}, f[u, v] + f[u + h, v + h*f[u, v]]][x[k - 1], y[k - 1]];
k++];
Array[y, Nsteps] (* to see all Nsteps values *)
y[Nsteps] (* to see the last value *)
Make a computational experiment: in the improved Euler algorithm, using the corrector value as the next prediction, and
only after the second iteration use the trapezoid rule.
The ``improved'' predictor-corrector algorithm:
k_1 &= f(x_k , y_k ) ,
\\
k_2 &= f(x_{k+1} , y_k + h\,k_1 ) ,
\\
k_3 &= y_k + \frac{h}{2} \left( k_1 + k_2 \right) ,
\\
y_{k+1} &= y_k + \frac{h}{2} \left( k_1 + k_3 \right) ,
\end{align*} \]
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps];
Do[xnew = xold + h;
k1 = f[xold, yold];
k2 = f[xold + h, yold + k1*h];
k3 = yold + .5*(k1 + k2)*h;
ynew = yold + .5*(k1 + f[xnew, k3])*h;
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
Then we apply this code to numerically solve the initial value problem \( y' = (1+x)\,\sqrt{y} , \quad y(0) =1 \) with step size h=0.1:
heunit[f, {x, 0, 2}, {y, 1}, 20]
V. Modified Euler Method / Midpoint Method
The Modified Euler’s method is also called the midpoint approximation. This method reevaluates the slope throughout the approximation. Instead of taking approximations with slopes provided in the function, this method attempts to calculate more accurate approximations by calculating slopes halfway through the line segment. The syntax of the Modified Euler’s method involves the sum of the current y term and the product of h with the function in terms of the sum of the current x and half of h (which defines the x value) and the sum of the current y and the product of the h value and the function in terms of the current x and y values (which defines the y value).
The midpoint method can be shown to have a local error of 2, so it is second-order accurate.
The midpoint method is implemented in NDSolve as "ExplicitMidpoint":
Modified Euler formula or explicit midpoint rule or midpoint Euler algorithm:
Another option:
h = 0.1
K = IntegerPart[1.2/h] (* if the value at x=1.2 needed *)
y[0] = 1 (* initial condition *)
Then implement modified Euler method/ midpoint rule:
y[K]
Let’s take all of the approximations and the exact values to compare the accuracy of the approximation methods:
| x values | Exact | Euler | Backwards Euler | Trapezoid | Improved Euler | Modified Euler |
| 0.1 | 1.049370088 | 1.050000000 | 1.057930422 | 1.0493676 | 1.049390244 | 1.049382716 |
| 0.2 | 1.097463112 | 1.098780488 | 1.118582822 | 1.0974587 | 1.097594738 | 1.097488615 |
| 0.3 | 1.144258727 | 1.146316720 | 1.182399701 | 1.1442530 | 1.144322927 | 1.144297185 |
| 0.4 | 1.189743990 | 1.192590526 | 1.249960866 | 1.1897374 | 1.189831648 | 1.189795330 |
| 0.5 | 1.233913263 | 1.237590400 | 1.322052861 | 1.2339064 | 1.234025039 | 1.233977276 |
| 0.6 | 1.276767932 | 1.281311430 | 1.399792164 | 1.2767613 | 1.276904264 | 1.276844291 |
| 0.7 | 1.318315972 | 1.323755068 | 1.484864962 | 1.3183102 | 1.318477088 | 1.318404257 |
| 0.8 | 1.358571394 | 1.364928769 | 1.580059507 | 1.3585670 | 1.358757326 | 1.358671110 |
| 0.9 | 1.397553600 | 1.404845524 | 1.690720431 | 1.3975511 | 1.397764204 | 1.397664201 |
| 1.0 | 1.435286691 | 1.443523310 | 1.830688225 | 1.4352865 | 1.435521666 | 1.435407596 |
| Accuracy | N/A | 99.4261% | 72.4513% | 99.9999% | 99.9836% | 99.9916% |
Notice how each improved approximation approaches the exact value, which results in the modified Euler’s method being the most accurate method of approximating the value of the differential equation y’=1/(2*x-3*y+5). Note that the modified Euler’s method isn’t always the most accurate approximation method, as the improved Euler’s method can be more accurate than the modified Euler’s method depending on the differential equation in question.
1.3.3. Polynomial Approximations
II. Polynomial Approximations
Since the first order Taylor series approximation is identical with Euler’s method,
we start with the second order one. Now let us
take example where y’=1/(2x-3y+5), y(0)=1 and let us try to find out y(1).
Approximations using Taylor series expansions is a much easier task to perform using Mathematica because there are many iterations of the same calculations performed in order to achieve the desired answer.
Approximations with using Taylor series expansions in the first-order is actually the Euler algorithm: yn+1=yn+hf(xn,yn)=yn+h/(1-2xn+yn), n=0,1,2,…
They are similar in that they both take in the current term and add the approximate deviation to the next term in order to yield the value of the next term. If you look at the Mathematica file, the approximation of the sequence is the last y term of the sequence, which in this case is y10=1.443523310.
For each step in the sequence, the expansion requires 3 addition, 1 subtraction, 3 multiplication, and 1 division operations. Since there are 8 steps to this sequence, in order to obtain the desired approximation, the code performs 80 operations, which would be hectic work to do by hand.
II. Second Order Polynomial Approximation
The second order Taylor approximation is just adding the second order differential deviation to the next term in the same equation used for the first order Taylor expansion. The approximation is y10=1.435290196. This algorithm requires at least 22 operations per step, which means that the entire sequence requires 220 steps. However, this is not significant since Mathematica does all the work.
f2[x_,y_] = D[f[x,y],x] + D[f[x,y],y] f[x,y]
f3[x_,y_] = D[f2[x,y],x] + D[f2[x,y],y] f[x,y]
euler2[{x_,y_}] ={x+h,y+h*f[x,y]+(h^2/2)*f2[x,y]}
Expand[euler2[{x,y}]]
e2t=NestList[euler2,{x0,y0},10]
Since the first order Taylor series approximation is identical with Euler’s method,
we start with the second order one. Now let us
take example where y’=1/(2x-3y+5), y(0)=1 and let us try to find out y(1).
h:=0.1;
f1[x_, y_] := 1 / (2 x - 3 y + 5)
fx[x_, y_] := D[f1[a, b], a] /. {a -> x, b -> y}
fy[x_, y_] := D[f1[a, b], b] /. {a -> x, b -> y}
f2[x_, y_] := fx[x, y] + fy[x, y] * f1[x, y]
y[0] = 1;
Do[y[n + 1] = y[n] + h * f1[h n, y[n]] + 1 / 2 * h^2 * f2[h n, y[n]], {n, 0, 9}]
y[10]
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[stepsize];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
\[Phi]2 = fold + (h/2)*((D[f, x] /. {x -> xold, y -> yold}) + (D[f, y] /. {x -> xold,
y -> yold})*(f /. {x -> xold, y -> yold}));
ynew = yold + h*\[Phi]2;
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {(xn - x0)/stepsize}];
Return[sollist]]
0.324428}, {0.5, 0.385342}, {0.6, 0.440086}, {0.7, 0.489518}, {0.8,
0.53438}, {0.9, 0.575305}, {1., 0.612825}}
Using Mathematica command NDSolve, we check the obtained value:
Another example.
f1[x_,y_]=D[f[x,y],x]+f[x,y]*D[f[x,y],y]
y[1] = 1; h =0.1;
a = 0; b = 1; n = Floor[(b-a)/h];
Do[x[i] = 0.0 + (i-1)*h, {i,1,n+1}]
Do[{k1=f1[x[i],y[i]],
y[i+1] = y[i] + h*f[x[i],y[i]] +h*h/2*k1}, {i,1,n}]
Do[Print[x[i], " ", y[i]],{i,1,n+1}]
III. Third Order Polynomial Approximation
The third order Taylor approximation is adding a third order differential deviation to the equation for the 2nd order expansion. The approximation for this is y10=1.435283295.
Here is the syntax for the third order Taylor approximation (which takes too long to execute):
f1[x_, y_] := 1 / (2 x - 3 y + 5)
fx[x_, y_] := D[f1[a, b], a] /. {a -> x, b -> y}
fy[x_, y_] := D[f1[a, b], b] /. {a -> x, b -> y}
f2[x_, y_] := fx[x, y] + fy[x, y] * f1[x, y]
fxx[x_, y_] := D[fx[a, b], a] /. {a -> x, b -> y}
fxy[x_, y_] := D[fx[a, b], b] /. {a -> x, b -> y}
fyy[x_, y_] := D[fy[a, b], b] /. {a -> x, b -> y}
f3[x_, y_] := fxx[x, y] + 2 * fxy[x, y] * f1[x, y] +
fyy[x, y] * (f1[x, y])^2 + fx[x, y] * fy[x, y] + (fy[x, y])^2 * f1[x, y]
y[0] = 1;
Do[y[n + 1] = y[n] + h * f1[h n, y[n]] +
1 / 2 * h^2 * f2[h n, y[n]] + 1 / 6 * h^3 * f3[h n, y[n]], {n, 0, 9}]
y[10]
The total number of numerical operations here is 420. It is obvious at this point why using mathematical programs such as Mathematica is a desired approach for such problems.
taylor3[f_, {x_, x0_, xn_}, {y_, y0_}, stepsize_] :=
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[stepsize];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
\[Phi]2 =
fold + (h/
2)*((D[f, x] /. {x -> xold,
y -> yold}) + (D[f, y] /. {x -> xold,
y -> yold})*(f /. {x -> xold, y -> yold}));
\[Alpha] = (D[f, {x, 2}] /. {x -> xold, y -> yold}) +
2*(D[f, x, y] /. {x -> xold, y -> yold})*(f /. {x -> xold,
y -> yold}) + (D[f, {y, 2}] /. {x -> xold,
y -> yold})*(f /. {x -> xold, y -> yold})^2 + (D[f,
x] /. {x -> xold, y -> yold})*(D[f, y] /. {x -> xold,
y -> yold}) + (D[f, y] /. {x -> xold,
y -> yold})^2*(f /. {x -> xold, y -> yold});
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {(xn - x0)/stepsize}];
Return[sollist]]
0.324853}, {0.5, 0.385962}, {0.6, 0.440895}, {0.7, 0.4905}, {0.8,
0.535517}, {0.9, 0.576577}, {1., 0.614216}}
Another example:
f1[x_,y_]=D[f[x,y],x]+f[x,y]*D[f[x,y],y]
f2[x_,y_]=D[f[x,y],x,x]+2*f[x,y]*D[f[x,y],x,y] + D[f[x,y],y,y]*f[x,y]*f[x,y] + D[f[x,y],x]*D[f[x,y],y] +f[x,y]*(D[f[x,y],y])^2
y[1] = 1; h =0.1;
a = 0; b = 1; n = Floor[(b-a)/h];
Do[x[i] = 0.0 + (i-1)*h, {i,1,n+1}]
Do[{k1=f1[x[i],y[i]],
k2=f2[x[i],y[i]],
y[i+1] = y[i] + h*f[x[i],y[i]] +h*h/2*k1 + k2/6*h^3}, {i,1,n}]
Do[Print[x[i], " ", y[i]],{i,1,n+1}]
IV. Regular Plotting vs Log-Plotting
Plotting the absolute value of the errors for Taylor approximations, such as the ones from the previous example, is fairly easy to do in normal plotting.
The normal plotting procedure involves taking all of the information regarding the Taylor approximations and putting them into one file, then calculate the exact solution, then find the difference between each approximation and the exact solution, and plotting the solution.
Looking at the code, the syntax is pretty much self-explanatory. The only part that may confuse students is the syntax for the plot command. The plot command need not be in the same syntax as the file has it. If you wish to, you can alter the syntax to form a curve instead of dots.
Log-plotting is not much different than plotting normally. In other programs such as Mathematica, there are a couple of fixes to make, but in Maple only one line of code is required, as seen in the file. Make sure that before you use the logplot command to open the plots package.
1.3.4. Runge-Kutta Methods
Both previously discussed rules (improved Euler and modified Euler) are particular cases of the family of numerical methods known as the Runge-Kutta methods.
The idea of Runge--Kutta methods is to take successive (weighted) Euler steps to approximate a Taylor series. In this way function evaluations (and not derivatives) are used. For example, consider the one-step formulation of the midpoint method.
Extending the approach in (1), repeated function evaluation can be used to obtain higher-order methods. Denote the Runge--Kutta method for the approximate solution to an initial value problem at \( t_{n+1} = t_n +h \) by
where \( s \) is the number of stages.
It is generally assumed that the row-sum conditions hold:
c_i = \sum_{j=1}^s a_{i,j} , \qquad i=1,2,\ldots , s.
\]
These conditions effectively determine the points in time at which the function is sampled and are a particularly useful device in the derivation of high-order Runge--Kutta methods.
The coefficients of the method are free parameters that are chosen to satisfy a Taylor series expansion through some order in the time step \( h . \) In practice other conditions such as stability can also constrain the coefficients.
Explicit Runge--Kutta methods are a special case where the matrix A is strictly lower triangular:
a_{i,j} =0, \qquad j\ge i, \quad j=1,2,\ldots , s .
\]
It has become customary to denote the method coefficients \( {\bf c} = [c_i ]^T ,\ {\bf b} = [b_i]^T \) , and \( {\bf A} = [a_{i,j}] \) using a Butcher table, which has the following form for explicit Runge--Kutta methods.
The row-sum conditions can be visualized as summing across the rows of the table.
Notice that a consequence of explicitness is \( c_1 =0 ,\) so that the function is
sampled at the beginning of the current integration step.
Example.The Butcher table for the explicit midpoint method is given by:
See
http://reference.wolfram.com/language/tutorial/NDSolveExplicitRungeKutta.html
The Euler’s method is sometimes called the first order Runge-Kutta Method, and the Heun’s
method the second order one. In this section, we consider a family of Runge-Kutta methods. To make our exposition uniform, we choose the step size h=0.1, and test each algorithm on the following initial value problem:
Correspondingly, we define the slope function f[x_,y_]=x*x-y*y;
I. Second Order Runge-Kutta Approximations
Second Order Optimal Runge-Kutta Approximation when the step size is specified: \begin{equation} \label{E35.opt} y_{n+1} =y_n + \frac{h}{4}\,f(x_n , y_n ) + \frac{3h}{4} \,f\left( x_n + \frac{2h}{3} , y_n + \frac{2h}{3} \,f(x_n , y_n ) \right) , \quad n=0,1,2,\ldots . \end{equation}
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, x, y, n, steps,xnew, ynew,xthird,fn,k1},
steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
xthird = xold + 2*h/3;
fn = f [x -> xold, yold];
k1 = f[xthird, yold + fn*2*h/3];
ynew = yold + h*fn/4 + 3*h*k1/4;
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
RK2op[f, {1, 2}, 1, 0.1]
The same algorithm when the number of steps is specified:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, x, y, n, h,
xthird, fn, ynew, xnew, k1}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
xthird = xold + 2*h/3;
fn = f[xold, yold];
k1 = f[xthird, yold + fn*2*h/3];
ynew = yold + h*fn/4 + 3*h*k1/4;
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
RK2ops[f, {1, 2}, 1, 10]
2.07271}, {1.5, 2.44234}, {1.6, 2.86129}, {1.7, 3.33472}, {1.8,
3.86837}, {1.9, 4.46855}, {2., 5.14224}}
If only one final value is needed, then Return command should be replaced with
Second Order Ralson Approximation:
\begin{equation*} %\label{E35.ralson} y_{n+1} =y_n + \frac{h}{3}\,f(x_n , y_n ) + \frac{2h}{3} \,f\left( x_n + \frac{3h}{4} , y_n + \frac{3h}{4} \,f(x_n , y_n ) \right) , \quad n=0,1,2,\ldots . \end{equation*}Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, x, y, n, h, xnew,
ynew, xthird, k1, fn}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
xthird = xold + 3*h/4;
fn = f[xold, yold];
k1 = f[xthird, yold + fn*3*h/4];
ynew = yold + h*fn/3 + 2*h*k1/3;
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
Ralson2s[f, {1, 2}, 1, 10]
The same algorithm with fixed step size (which is denoted by h) is specified:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, x, y, n, steps,
xnew, ynew, xthird, k1, fn}, steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
xthird = xold + 3*h/4;
fn = f[xold, yold];
k1 = f[xthird, yold + fn*3*h/4];
ynew = yold + h*fn/3 + 2*h*k1/3;
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
Ralson2[f, {1, 2}, 1, 0.1]
Implicit Runge-Kutta of order 2:
\begin{equation} \label{E36.implicit} y_{n+1} = y_n + \frac{h}{2}\left( k_1 + k_2 \right) , \end{equation} where \begin{align*} k_1 &= f\left( x_n + \frac{\sqrt{3} -1}{2\sqrt{3}}\,h , \ y_n + \frac{h}{4}\,k_1 + \frac{\sqrt{3} -2}{4\sqrt{3}}\,hk_2\right) , \\ k_2 &= f\left( x_n + \frac{\sqrt{3} +1}{2\sqrt{3}}\,h , \ y_n + \frac{\sqrt{3} +2}{4\sqrt{3}}\,hk_1 + \frac{h}{4}\,k_2\right) , \end{align*}
First we present code when the step size (h) is given:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, steps},
steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
sol = FindRoot[{f1 ==
1/(3*(xold + (Sqrt[3] - 1)/(2*Sqrt[3])*h) -
2*(yold + h/4*f1 + (Sqrt[3] - 2)/(4*Sqrt[3])*h*f2) + 1),
f2 == 1/(3*(xold + (Sqrt[3] + 1)/(2*Sqrt[3])*h) -
2*(yold + h/4*f2 + (Sqrt[3] + 2)/(4*Sqrt[3])*h*f1) +
1)}, {{f1, fold}, {f2, fold}}];
ynew = yold + (h/2)*(sol[[1, 2]] + sol[[2, 2]]);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
Then the same algorithm when the number of steps is specified:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
sol = FindRoot[{f1 ==
1/(3*(xold + (Sqrt[3] - 1)/(2*Sqrt[3])*h) -
2*(yold + h/4*f1 + (Sqrt[3] - 2)/(4*Sqrt[3])*h*f2) + 1),
f2 == 1/(3*(xold + (Sqrt[3] + 1)/(2*Sqrt[3])*h) -
2*(yold + h/4*f2 + (Sqrt[3] + 2)/(4*Sqrt[3])*h*f1) +
1)}, {{f1, fold}, {f2, fold}}];
ynew = yold + (h/2)*(sol[[1, 2]] + sol[[2, 2]]);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
0.324916}, {0.5, 0.386028}, {0.6, 0.440961}, {0.7, 0.490565}, {0.8,
0.53558}, {0.9, 0.576638}, {1., 0.614275}}
Using Mathematica command NDSolve, we check the obtained value:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, steps},
steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
sol = FindRoot[{f1 ==
1/(3*(xold + (Sqrt[3] - 1)/(2*Sqrt[3])*h) -
2*(yold + h/4*f1 + (Sqrt[3] - 2)/(4*Sqrt[3])*h*f2) + 1),
f2 == 1/(3*(xold + (Sqrt[3] + 1)/(2*Sqrt[3])*h) -
2*(yold + h/4*f2 + (Sqrt[3] + 2)/(4*Sqrt[3])*h*f1) +
1)}, {{f1, fold}, {f2, fold}}];
ynew = yold + (h/2)*(sol[[1, 2]] + sol[[2, 2]]);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
II. Third Order Runge-Kutta Approximation
We start with the following third order algorithm credited to Kutta:
\begin{equation} \label{E35.9} y_{n+1} = y_n + \frac{h}{6}\, ( k_1 + 4 k_2 + k_3 ), \end{equation} where \[ \begin{array}{l} k_1 = f( x_n , y_n ) , \\ k_2 = f( x_n + h/2 , y_n + k_1 h/2 ) , \\ k_3 = f( x_n +h , y_n + 2h k_2 - h k_1 ) . \end{array} \]Block[{xold = x0, yold = y0, xhalf, xnew, ynew, sollist = {{x0, y0}},
x, y, h}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
xhalf = xold + h/2;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xhalf, y -> yold + k1*h/2};
k3 = f /. {x -> xnew, y -> yold + k2*h*2 - h*k1};
ynew = yold + (h/6)*(k1 + 4*k2 + k3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
1.14076}, {1.5, 1.21277}, {1.6, 1.29588}, {1.7, 1.38818}, {1.8,
1.48777}, {1.9, 1.59285}, {2., 1.70178}}
If you want to see only the last value (or any other particular value) use its modification:
Block[{xold = x0, yold = y0, xnew, xhalf, ynew, sollist = {{x0, y0}},
x, y, n, steps}, steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
xhalf = xold + h/2;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xhalf, y -> yold + k1*h/2};
k3 = f /. {x -> xnew, y -> yold + k2*h*2 - h*k1};
ynew = yold + (h/6)*(k1 + 4*k2 + k3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
III. The Nystrom Algorithm
The Nystrom algorithm:
\begin{equation} \label{E35.nystrom} y_{n+1} =y_n + \frac{h}{8}\,(2k_1 + 3k_2 + 3k_3 ), \qquad n=0,1,2,\ldots , \end{equation} where \[ k_1 = f(x_n , y_n ), \ k_2 = f\left( x_n + \frac{2h}{3} , y_n + \frac{2h}{3}\,k_1 \right) , \ k_3 = f\left( x_n + \frac{2h}{3} , y_n + \frac{2h}{3}\,k_2 \right) ; \]Block[{xold = x0, yold = y0, xnew, xthird, ynew,
sollist = {{x0, y0}}, x, y, n, h}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
xthird = xold + 2*h/3;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xthird, y -> yold + k1*h*2/3};
k3 = f /. {x -> xthird, y -> yold + k2*h*2/3};
ynew = yold + (h/8)*(2*k1 + 3*k2 + 3*k3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
Block[{xold = x0, yold = y0, xnew, xthird, ynew, k1,k2,k3,
sollist = {{x0, y0}}, x, y, n, steps}, steps = N[(xn - x0)/h];
Do[xnew = xold + h;
xthird = xold + 2*h/3;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xthird, y -> yold + k1*h*2/3};
k3 = f /. {x -> xthird, y -> yold + k2*h*2/3};
ynew = yold + (h/8)*(2*k1 + 3*k2 + 3*k3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
Example.
0.324968}, {0.5, 0.386087}, {0.6, 0.441026}, {0.7, 0.490635}, {0.8,
0.535654}, {0.9, 0.576716}, {1., 0.614356}}
IV. The Nearly Optimal Algorithm
The nearly optimal algorithm (used in MATLAB ode23)
\begin{equation} \label{E35.optimal} y_{n+1} =y_n + \frac{h}{9} \,(2k_1 + 3k_2 + 4k_3 ), \qquad n=0,1,2,\ldots , \end{equation} in which the stages are computed according to \[ k_1 = f(x_n , y_n ), \quad k_2 = f \left( x_n + \frac{h}{2} , y_n + \frac{h}{2}\,k_1 \right) , \quad k_3 = f \left( x_n + \frac{3h}{4} , y_n + \frac{3h}{4}\,k_2 \right) ; \]Block[{xold = x0, yold = y0, xnew, xhalf, ynew, k1, k2, k3,
sollist = {{x0, y0}}, x, y, n, h}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
xhalf = xold + h/2;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xhalf, y -> yold + k1*h/2};
k3 = f /. {x -> xold + 3*h/4, y -> yold + k2*h*3/4};
ynew = yold + (h/9)*(2*k1 + 3*k2 + 4*k3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
The same algorithm when the step size is specified:
Block[{xold = x0, yold = y0, xnew, xhalf, ynew, k1, k2, k3,
sollist = {{x0, y0}}, x, y, n, steps}, steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
xhalf = xold + h/2;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xhalf, y -> yold + k1*h/2};
k3 = f /. {x -> xold + 3*h/4, y -> yold + k2*h*3/4};
ynew = yold + (h/9)*(2*k1 + 3*k2 + 4*k3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
V. The Heun Algorithm
Heun's algorithm:
\begin{equation} \label{E35.heun} y_{n+1} =y_n + \frac{h}{4} \,(k_1 + 3k_3 ), \qquad n=0,1,2,\ldots , \end{equation} where \[ k_1 = f(x_n , y_n ), \ k_2 = f\left( x_n + \frac{h}{3} , y_n + \frac{h}{3}\,k_1 \right) , \ k_3 = f\left( x_n + \frac{2h}{3} , y_n + \frac{2h}{3}\,k_2 \right) . \]Block[{xold = x0, yold = y0, xnew, xhalf, ynew, k1, k2, k3,
sollist = {{x0, y0}}, x, y, n, h}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
xthird = xold + h/3;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xthird, y -> yold + k1*h/3};
k3 = f /. {x -> xold + 2*h/3, y -> yold + k2*h*2/3};
ynew = yold + (h/4)*(k1 + 3*k3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
Block[{xold = x0, yold = y0, xnew, xhalf, ynew, k1, k2, k3,
sollist = {{x0, y0}}, x, y, n, steps}, steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
xthird = xold + h/3;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xthird, y -> yold + k1*h/3};
k3 = f /. {x -> xold + 2*h/3, y -> yold + k2*h*2/3};
ynew = yold + (h/4)*(k1 + 3*k3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
0.324932}, {0.5, 0.386046}, {0.6, 0.440981}, {0.7, 0.490586}, {0.8,
0.535602}, {0.9, 0.576662}, {1., 0.6143}}
0.324932}, {0.5, 0.386046}, {0.6, 0.440981}, {0.7, 0.490586}, {0.8,
0.535602}, {0.9, 0.576662}, {1., 0.6143}}
VI. Bogacki and Shampine Approximation
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
f2 = f /. {x -> xold + h/2, y -> yold + fold*h/2};
f3 = f /. {x -> xold + 3*h/4, y -> yold + f2*3*h/4};
ynew = yold + (h/9)*(2*fold + 3*f2 + 4*f3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[stepsize];
Do[xnew = xold + h;
fold = f /. {x -> xold, y -> yold};
f2 = f /. {x -> xold + h/2, y -> yold + fold*h/2};
f3 = f /. {x -> xold + 3*h/4, y -> yold + f2*3*h/4};
ynew = yold + (h/9)*(2*fold + 3*f2 + 4*f3);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {(xn - x0)/stepsize}];
Return[sollist]]
0.324963}, {0.5, 0.386082}, {0.6, 0.441021}, {0.7, 0.490629}, {0.8,
0.535647}, {0.9, 0.576709}, {1., 0.614349}}
VII. Fourth Order Runge-Kutta Approximation
Let us introduce the classical fourth order Runge-Kutta algorithm:
\begin{equation} \label{E35.10} y_{n+1} = y_n + \frac{h}{6}\, ( k_1 + 2 k_2 + 2 k_3 + k_4 ), \end{equation} where \[ \begin{array}{l} k_1 = f_n = f(x_n , y_n ), \\ k_2 = f\left( x_n + \frac{h}{2}, y_n + \frac{h}{2} k_1 \right) , \\ k_3 =f\left( x_n + \frac{h}{2}, y_n + \frac{h}{2} k_2 \right) , \\ k_4 = f( x_n + h, y_n + h k_3 ). \end{array} \]We revisit our example, and solve it in the following way:
f[x_, y_] := x^2 - y^2 (* this function is chosen as an example *)
y[0] = 1;
Do[k1 = h f[h n, y[n]];
k2 = h f[h (n + .5), y[n] + k1 / 2];
k3 = h f[h (n + .5), y[n] + k2 / 2];
k4 = h f[h (n + 1), y[n] + k3];
y[n + 1] = y[n] + 1 / 6 * (k1 + 2 k2 + 2 k3 + k4),
{n, 0, 9}]
y[10]
Other codes of classical Runge-Kutta method (the first one is when the step size h is specified, and another one when the number of steps is given):
RK4[f_, {x0_, xn_}, y0_, h_] :=
Block[{xold = x0, yold = y0, xhalf, xnew, ynew, k1, k2, k3, k4,
sollist = {{x0, y0}}, x, y, n, steps}, steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
xhalf = xold + h/2;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xhalf, y -> yold + k1*h/2};
k3 = f /. {x -> xhalf, y -> yold + k2*h/2};
k4 = f /. {x -> xnew, y -> yold + k3*h};
ynew = yold + (h/6)*(k1 + 2*k2 + 2*k3 + k4);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Another version when the number of steps is specified.
Block[{xold = x0, yold = y0, xhalf, xnew, ynew, k1, k2, k3, k4,
sollist = {{x0, y0}}, x, y, n, h}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
xhalf = xold + h/2;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xhalf, y -> yold + k1*h/2};
k3 = f /. {x -> xhalf, y -> yold + k2*h/2};
k4 = f /. {x -> xnew, y -> yold + k3*h};
ynew = yold + (h/6)*(k1 + 2*k2 + 2*k3 + k4);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
RK4s[f[x, y], {0, 1}, 0, 10] (* 10 is the number of steps *)
RK4[f[x, y], {0, 1}, 0, 0.1] (* h=0.1 is the step size *)
Here is a slightly different version of the above code:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
k1 = N[f[xold, yold]];
k2 = N[f[xold + h/2, yold + h*k1/2]];
k3 = N[f[xold + h/2, yold + k2*h/2]];
k4 = N[f[xold + h, yold + k3*h]];
ynew = N[yold + h*(k1 + 2*k2 + 2*k3 + k4)/6];
sollist = Append[sollist, {xnew, ynew}];
xold = xnew; yold = ynew, {steps}];
Return[sollist]]
RK4s[f[x, y], {1, 2}, 1, 10]
y[1] = 1; h =0.1;
a = 0; b = 2; n = Floor[(b-a)/h];
Do[x[i] = 0.0 + (i-1)*h, {i,1,n+1}]
Do[{k1 = f[x[i],y[i]],
k2 = f[x[i]+h/2, y[i]+h*k1/2],
k3 = f[x[i]+h/2, y[i]+h*k2/2],
k4 = f[x[i]+h, y[i]+h*k3],
k = (k1+2*k2+2*k3+k4)/6;
y[i+1] = y[i] + k*h}, {i,1,n}]
Do[Print[x[i], " ", y[i]],{i,1,n+1}]
Kutta's algorithm of order four:
Block[{xold = x0, yold = y0, xnew, ynew, k1, k2, k3, k4,
sollist = {{x0, y0}}, x, y, n, h}, h = N[(xn - x0)/steps];
Do[xnew = xold + h;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xold + h/3, y -> yold + k1*h/3};
k3 = f /. {x -> xold + 2*h/3, y -> yold - h*k1/3 + k2*h};
k4 = f /. {x -> xnew, y -> yold + h*(k1 - k2 + k3)};
ynew = yold + (h/8)*(k1 + 3*k2 + 3*k3 + k4);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew; yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
kutta4s[f[x, y], {1, 2}, 1, 10]
Here is a slightly different version of Kutta's algorithm:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps];
Do[xnew = xold + h;
k1 = N[f[xold, yold]];
k2 = N[f[xold + h/3, yold + h*k1/3]];
k3 = N[f[xold + h*2/3, yold - h*k1/3 + k2*h]];
k4 = N[f[xold + h, yold + k3*h - k2*h + h*k1]];
ynew = N[yold + h*(k1 + 3*k2 + 3*k3 + k4)/8];
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
Block[{xold = x0, yold = y0, xnew, ynew, k1, k2, k3, k4,
sollist = {{x0, y0}}, x, y, n, steps}, steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xold + h/3, y -> yold + k1*h/3};
k3 = f /. {x -> xold + 2*h/3, y -> yold - h*k1/3 + k2*h};
k4 = f /. {x -> xnew, y -> yold + h*(k1 - k2 + k3)};
ynew = yold + (h/8)*(k1 + 3*k2 + 3*k3 + k4);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
kutta4[f[x, y], {1, 2}, 1, 0.1]
Now we apply the same code with modified last line
0.32492}, {0.5, 0.386033}, {0.6, 0.440966}, {0.7, 0.49057}, {0.8,
0.535585}, {0.9, 0.576644}, {1., 0.614281}}
Another version:
y[1] = 1; h =0.1;
a = 0; b = 2; n = Floor[(b-a)/h];
Do[x[i] = 0.0 + (i-1)*h, {i,1,n+1}]
Do[{k1 = f[x[i],y[i]],
k2 = f[x[i]+h/3, y[i]+h*k1/3],
k3 = f[x[i]+h*2/3, y[i]+h*k2-h*k1/3],
k4 = f[x[i]+h, y[i]+h*k3+h*k1-h*k2],
k = (k1+3*k2+3*k3+k4)/8;
y[i+1] = y[i] + k*h}, {i,1,n}]
Do[Print[x[i], " ", y[i]],{i,1,n+1}]
Gill's method:
\begin{equation} \label{E35.12}
y_{n+1} = y_n + \frac{h}{6} \left[ k_1 + 2 \left( 1 - \frac{1}{\sqrt{2}}
\right) k_2 + 2 \left( 1 + \frac{1}{\sqrt{2}} \right) k_3 + k_4 \right] ,
\end{equation}
where
\[
\begin{array}{l}
k_1 = f(x_n , y_n ),
\\
k_2 = f\left( x_n + \frac{h}{2}\, , y_n + \frac{h}{2}\, k_1 \right) ,
\\
k_3 =f\left( x_n + \frac{h}{2}\, , y_n - \left( \frac{1}{2} - \frac{1}{\sqrt{2}}
\right) h k_1 + \left( 1 - \frac{1}{\sqrt{2}} \right) h k_2 \right) ,
\\
k_4 = f( x_n + h, y_n - \frac{1}{\sqrt{2}} h k_2 + \left( 1 +
\frac{1}{\sqrt{2}} \right) h k_3 ).
\end{array}
\]
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, x, y, steps,
r2, xnew, ynew, xhalf, k1, k2, k3, k4},
steps = Round[(xn - x0)/h];
Do[xnew = xold + h;
xhalf = xold + h/2; r2 = 1/Sqrt[2];
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xhalf, y -> yold + k1*h/2};
k3 = f /. {x -> xhalf, y -> yold - h*k1*(1/2 - r2) + k2*h*(1 - r2)};
k4 = f /. {x -> xnew, y -> yold - r2*h*k2 + h*k3*(1 + r2)};
ynew = yold + (h/6)*(k1 + 2*(1 - r2)*k2 + 2*(1 + r2)*k3 + k4);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
gill4[f[x, y], {1, 2}, 1, 0.1]
Another version:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, x, y, h, r2, xnew, ynew, xhalf, k1, k2, k3, k4},
h = N[(xn - x0)/steps];
Do[xnew = xold + h; xhalf = xold + h/2;
r2 = 1/Sqrt[2]; k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xhalf, y -> yold + k1*h/2};
k3 = f /. {x -> xhalf, y -> yold - h*k1*(1/2 - r2) + k2*h*(1 - r2)};
k4 = f /. {x -> xnew, y -> yold - r2*h*k2 + h*k3*(1 + r2)};
ynew = yold + (h/6)*(k1 + 2*(1 - r2)*k2 + 2*(1 + r2)*k3 + k4);
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist[[steps + 1]]]]
Then we exercute the code:
gill4s[f[x, y], {1, 2}, 1, 10]
k1 = N[f[xold, yold]];
k2 = N[f[xold + h/2, yold + h*k1/2]];
k3 = N[ f[xold + h/2, yold - h*k1*(1/2 - 1/Sqrt[2]) + k2*h*(1 - 1/Sqrt[2])]];
k4 = N[f[xold + h, yold - k2*h/Sqrt[2] + h*k3*(1 + 1/Sqrt[2])]];
ynew = N[yold + h*(k1 + 2*(1 - 1/Sqrt[2])*k2 + 2*(1 + 1/Sqrt[2])*k3 + k4)/6];
sollist = Flatten[Append[sollist, {xnew, ynew}]];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
Another version:
y[1] = 1; h =0.1;
a = 0; b = 2; n = Floor[(b-a)/h];
Do[x[i] = 0.0 + (i-1)*h, {i,1,n+1}]
f[x_,y_] = 1/y^3 - 2*x^2;
ap = N[1+1/Sqrt[2]];
am = N[1-1/Sqrt[2]];
amm = N[1/2-1/Sqrt[2]];
Do[{k1 = N[f[x[i],y[i]]],
k2 = N[f[x[i]+h/2, y[i]+h*k1/2]],
k3 = N[f[x[i]+h/2, y[i]+h*k2*am-h*k1*amm]],
k4 = N[f[x[i]+h, y[i]-h*k2/Sqrt[2]+h*k3*ap]],
k = N[(k1+2*k2*am+2*k3*ap+k4)/6];
y[i+1] = y[i] + k*h}, {i,1,n}]
Do[Print[x[i], " ", y[i]],{i,1,n+1}]
Fifth order Butcher's method:
\begin{equation} \label{E36.butcher}
y_{k+1} = y_k + \frac{h}{90} \left( 7k_1 + 32 k_3 + 12 k_4 + 32 k_5 +
7 k_6 \right) , \qquad k=0,1,\ldots ,
\end{equation}
where
\[
\begin{align*}
k_1 &= f(x_k , y_k ), \qquad &k_2 = f \left( x_k + h/4 , y_k + hk_1
/4 \right) ,
\\
k_3 &= f \left( x_k + h/4 , y_k + k_1 h/8 + k_2
h/8 \right), \qquad &k_4 = f \left( x_k + h/2 , y_k - k_2 h/2 + k_3
h \right) ,
\\
k_5 &= f \left( x_k + 3h/4 , y_k + 3k_1 h/16 +9 k_4
h/16 \right) , \qquad &k_6 = f \left( x_k + h , y_k - 3k_1 h/7 + 2k_2 h/7 +
12k_3 h/7 -12k_4 h/7 + 8k_5 h/7 \right) .
\end{align*}
\]
y[1] = 1; h =0.1;
a = 0; b = 2; n = Floor[(b-a)/h];
Do[x[i] = 0.0 + (i-1)*h, {i,1,n+1}]
f[x_,y_] = 1/y^3 - 2*x^2;
Do[{k1 = N[f[x[i],y[i]]],
k2 = N[f[x[i]+h/4, y[i]+h*k1/4]],
k3 = N[f[x[i]+h/4, y[i]+h*k1/8+h*k2/8]],
k4 = N[f[x[i]+h/2, y[i]+h*k3-k2*h/2]],
k5 = N[f[x[i]+h*3/4, y[i]+3*h*k1/16+9*h*k4/16]],
k6 = N[f[x[i]+h, y[i]-3*h*k1/7+2*h*k2/7 +12*k3*h/7-12*h*k4/7 +8*k5*h/7]],
k = N[(7*k1+32*k3+12*k4+32*k5 +7*k6)/90];
y[i+1] = y[i] + k*h}, {i,1,n}]
Do[Print[x[i], " ", y[i]],{i,1,n+1}]
Another version of Butcher's method:
Block[{xold = x0, yold = y0, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps];
Do[xnew = xold + h;
(* Print["h= ", h, " xold= ", xold, " yold= ", yold]; *)
k1 = N[f[xold, yold]];
k2 = N[f[xold + h/4, yold + h*k1/4]];
k3 = N[f[xold + h/4, yold + h*k1/8 + k2*h/8]];
k4 = N[f[xold + h/2, yold - k2*h/2 + k3*h]];
k5 = N[f[xold + 3*h/4, yold + 3*k1*h/16 + 9*k4*h/16]];
k6 = N[
f[xnew, yold + 2*k2*h/7 - 3*k1*h/7 + 12*k3*h/7 - 12*k4*h/7 +
8*k5*h/7]];
ynew = N[yold + h*(7*k1 + 32*k3 + 12*k4 + 32*k5 + 7*k6)/90];
sollist = Append[sollist, {xnew, ynew}];
xold = xnew;
yold = ynew, {steps}];
Return[sollist]]
Now we present an example of use this algorimth. Let \( f(x,y) = 1 -x +4y .\) Application of RK5 to solve numerically the initial value problem
Now, let’s compare the exact value and the values determined by the polynomial approximations and the Runge-Kutta method.
| x values | Exact | First Order Polynomial | Second Order Polynomial | Third Order Polynomial | Runge-Kutta Method |
| 0.1 | 1.049370088 | 1.050000000 | 1.049375000 | 1.049369792 | 1.049370096 |
| 0.2 | 1.097463112 | 1.098780488 | 1.097472078 | 1.097462488 | 1.097463129 |
| 0.3 | 1.144258727 | 1.146316720 | 1.144270767 | 1.144257750 | 1.144258752 |
| 0.4 | 1.189743990 | 1.192590526 | 1.189758039 | 1.189742647 | 1.189744023 |
| 0.5 | 1.233913263 | 1.237590400 | 1.233928208 | 1.233911548 | 1.233913304 |
| 0.6 | 1.276767932 | 1.281311430 | 1.276782652 | 1.276765849 | 1.276767980 |
| 0.7 | 1.318315972 | 1.323755068 | 1.318329371 | 1.318313532 | 1.318316028 |
| 0.8 | 1.358571394 | 1.364928769 | 1.358582430 | 1.358568614 | 1.358571457 |
| 0.9 | 1.397553600 | 1.404845524 | 1.397561307 | 1.397550500 | 1.397553670 |
| 1.0 | 1.435286691 | 1.443523310 | 1.435290196 | 1.435283295 | 1.435286767 |
| Accuracy | N/A | 99.4261% | 99.99975% | 99.99976% | 99.99999% |
You will notice that compared to the Euler methods, these methods of approximation are much more accurate because they contains much more iterations of calculations than the Euler methods, which increases the accuracy of the resulting y-value for each of the above methods.
V. Method Comparison
Sometimes you may be interested to find out what methods are being used in NDSolve.
Here you can see the coefficients of the default 2(1) embedded pair.
{{{1}, {1/2, 1/2}}, {1/2, 1/2, 0}, {1, 1}, {-(1/2), 2/3, -(1/6)}}
You also may want to compare some of the different methods to see how
they perform for a specific problem.
Implicit Runge--Kutta methods have a number of desirable properties.
The Gauss--Legendre methods, for example, are self-adjoint, meaning
that they provide the same solution when integrating forward or
backward in time.
http://reference.wolfram.com/language/tutorial/NDSolveImplicitRungeKutta.html
A generic framework for implicit Runge--Kutta methods has been implemented. The focus so far is on methods with interesting geometric properties and currently covers the following schemes:
"ImplicitRungeKuttaGaussCoefficients"
"ImplicitRungeKuttaLobattoIIIACoefficients"
"ImplicitRungeKuttaLobattoIIIBCoefficients"
"ImplicitRungeKuttaLobattoIIICCoefficients"
"ImplicitRungeKuttaRadauIACoefficients"
"ImplicitRungeKuttaRadauIIACoefficients"
The derivation of the method coefficients can be carried out to arbitrary order and arbitrary precision.
3.5. Multistep Methods
Predictor-corrector of order 2:
Block[{xold = x0, yold = y0, ynew = y1, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps]; sollist = Append[sollist, {x0 + h, y1}];
Do[xnew = xold + h;
xnew2 = xold + h*2;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xnew, y -> ynew};
abnew = ynew + (3*h/2)*k2 - h*k1/2;
k3 = f /. {x -> xnew2, y -> abnew};
bm = ynew + h*k2/2 + h*k3/2;
sollist = Append[sollist, {xnew2, bm}];
xold = xnew;
yold = ynew; ynew = bm, {steps}];
Return[sollist[[steps + 1]]]]
To apply yjis method, use the following commands:
ABM2[f[x, y], {x, 0, 1.0}, {y, 1, Exp[0.1*0.1]}, 10]
If you want to see the whole table of values:
Block[{xold = x0, yold = y0, ynew = y1, sollist = {{x0, y0}}, h},
h = N[(xn - x0)/steps]; sollist = Append[sollist, {x0 + h, y1}];
Do[xnew = xold + h;
xnew2 = xold + h*2;
k1 = f /. {x -> xold, y -> yold};
k2 = f /. {x -> xnew, y -> ynew};
abnew = ynew + (3*h/2)*k2 - h*k1/2;
k3 = f /. {x -> xnew2, y -> abnew};
bm = ynew + h*k2/2 + h*k3/2;
sollist = Append[sollist, {xnew2, bm}];
xold = xnew;
yold = ynew; ynew = bm, {steps}];
Return[sollist]]
Example.
ABM2[f[x, y], {x, 0, 1.0}, {y, 1, Exp[0.1*0.1]}, 10]
Predictor-corrector method of order 2:
Nsteps = 20; (* number of steps *)
h=0.1; (* step size *)
f[u_, v_] := (* define the slope function *)
Array[x, Nsteps]; Array[y, Nsteps];
i=1;
While[i < Nsteps + 1, x[i] = x[i - 1] + h; i++]; (* Generate uniform grid of points *)
y[1]= (* the value at the first mesh point must be specified *)
k=1;
While[k < Nsteps + 1,
predictor =
y[k] + 3*h/2*f[x[k], y[k]] - h*f[x[k - 1], y[k - 1]]/2 ;
y[k + 1] = y[k] + h*f[x[k], y[k]]/2 + h*f[x[k + 1], predictor]/2;
k++];
y[20]
or using Function command
predictor =
y[k] + 3*h*Function[{u, v}, f[u, v]][x[k], y[k]]/2 -
h*Function[{u, v}, f[u, v]][x[k - 1], y[k - 1]]/2;
y[k + 1] =
y[k] + h*Function[{u, v}, f[u, v]][x[k], y[k]]/2 +
h*Function[{u, v}, f[u, v]][x[k + 1], predictor]/2;
k++];
Predictor-corrector of order 3:
Preprocessing includes:
Nsteps = number of steps
h = step size
f[u_,v_] = slope function
Initial values:
x[0] =
y[0] =
Generate first values using a single-step numerical method or actual solution:
y[1] =
y[2] =
Arrays of independent and dependent variables corresponding to uniform grid:
Array[x, Nsteps]; Array[y, Nsteps];
i=1;
While[i < Nsteps + 1, x[i] = x[i - 1] + h; i++];
While[k < Nsteps + 1,
predictor =
y[k] + 23*h*Function[{u, v}, f[u, v]][x[k], y[k]]/12 -
4*h*Function[{u, v}, f[u, v]][x[k - 1], y[k - 1]]/3 + 5*h*Function[{u, v}, f[u, v]][x[k - 2], y[k - 2]]/12;
y[k + 1] =
y[k] + 2*h*Function[{u, v}, f[u, v]][x[k], y[k]]/3 +
5*h*Function[{u, v}, f[u, v]][x[k + 1], predictor]/12 - h*Function[{u, v}, f[u, v]][x[k - 1], y[k - 1]]/12;
k++];
Variable coefficient recurence, corresponding to explicit Adams' method of the second order where the first value is determined from the actual solution (however, it can be found using any single-step method, say obtained by classical Runge-Kutta algorithm) can be solved numerically:
a[1] = Exp[h*h] (* this value was determined analytically *)
a[1] == 1 + (8*h*h + 5*h^4 + 2*h^6)/12}, a, {n, 1, 30}] (* or using Runge-Kutta-4 *)
RecurrenceTable[{a[n + 1] ==
a[n] + 3*h*h*n*a[n] - h*h*(n - 1)*a[n - 1], a[0] == 1, ]
1.3.6. Accuracy
Sometimes you may be interested to find out what methods are being used in NDSolve.
Here you can see the coefficients of the default 2(1) embedded pair.
{{{1}, {1/2, 1/2}}, {1/2, 1/2, 0}, {1, 1}, {-(1/2), 2/3, -(1/6)}}
You also may want to compare some of the different methods to see how they perform for a specific problem.
Implicit Runge--Kutta methods have a number of desirable properties.
The Gauss--Legendre methods, for example, are self-adjoint, meaning that they provide the same solution when integrating forward or backward in time.
http://reference.wolfram.com/language/tutorial/NDSolveImplicitRungeKutta.html
A generic framework for implicit Runge--Kutta methods has been implemented. The focus so far is on methods with interesting geometric properties and currently covers the following schemes:
"ImplicitRungeKuttaGaussCoefficients"
"ImplicitRungeKuttaLobattoIIIACoefficients"
"ImplicitRungeKuttaLobattoIIIBCoefficients"
"ImplicitRungeKuttaLobattoIIICCoefficients"
"ImplicitRungeKuttaRadauIACoefficients"
"ImplicitRungeKuttaRadauIIACoefficients"
The derivation of the method coefficients can be carried out to arbitrary order and arbitrary precision.
1.3.7. Numerov Method
1.3.8. Applications
Example
A 500 liter container initially contains 10 kg of salt. A brine mixture of 100 gramms
of salt per liter is entering the container at 6 liter per minute. The well-mixed contents
are being discharged from the tank at the rate of 6 liters per minute. Express the amount
of salt in the container as a function of time.
Salt is coming at the rate: 6*(0.1)=0.6 kg/min
d yin /dt =0.6 ; d yout/dt = 6x/500
dx/dt = 0.6 -6x/500 ; x(0)=10
Suppose that the rate of discharge is reduced to 5 liters per minute.
SolRule[t_] = Apart[x[t] /. First[%]]
10 (500 + t)^5))(3125000000000000 + 187500000000000 t +
937500000000 t^2 + 2500000000 t^3 + 3750000 t^4 + 3000 t^5 +
t^6)}}
Out[2]= 50 + t/10 - 1250000000000000/(500 + t)^5
To check the answer:
Together[SolRule'[t] == Together[6/10 - 5*SolRule[t]/(500 + t)]]
SolRule[0]
Out[4]= True
Out[5]= 10
I. Case Sensitivity