For a plot, it is necessary to define the independent variable that you are graphing with respect to. The independent and dependent variables can be defined either before using the plot function or within the plot function itself and must be matrices/vectors of equal sizes.

A typical code for a simple plot function in matlab is plot(ind_var, dep_var) , where ind_var and dep_var are vectors of the independent and dependent variables correspondingly. For instance, the command

We give examples of codes to display two graphs in two different figures.

Let the independent variable be x and the range be interval [0 , 2π] and we want to plot the function \( y = 2\,\sin 3x - 2\,\cos x . \)

The Octave command sequence is

x=linspace(0, 2*pi); % define and calculate a row vector of an independent variable x
y1 = 2*sin(3*x)-2*cos(x); % defining and calculating y1 as 2sin3x - 2cosx
y2 = sin(x) - cos(3*x)/3; % defining and calculating y2 as sinx - (cos3x)/3
figure       % opens new figure
plot(x,y1) % plots the first graph of x-y1
figure     % opens second new figure
plot(x,y2) % plots the second graph of x-y2

x = linspace(0, 2*pi);    % defining and calculating a row vector of an independent variable x
y1 = 2*sin(3*x)-2*cos(x); % defining and calculating y1 as as 2sin3x - 2cosx
y2 = sin(x) - cos(3*x)/3; % defining and calculating y2 as sinx - (cos3x)/3
figure          % opens new figure
plot(x,y1,x,y2) % plots graphs of y1(x) and y2(x)

x = linspace(0, 2*pi);  
y = 2*sin(3*x)-2*cos(x); 
title('Default view')
xlabel('#1')
figure
plot(x, y)
axis tight
title('axis tight')
xlabel('#2')
figure
plot(x, y)
axis equal
title('axis equal')
xlabel('#3')
figure
plot(x, y)
axis equal, axis tight
title('axis equal, axis tight')
xlabel('#4')

function plotting
  x=linspace(0, 2*pi);        % compute an argument
  y=2*sin(3*x)-2*cos(x);      % compute a function of argument x
  p1('Default view','#1',x,y) % plotting of the 1st graph
  p1('axis tight','#2',x,y)   % plotting of the 2nd graph
  axis tight                  % set axis to tight (graph #2)
  p1('axis equal','#3',x,y)   % plotting the 3rd graph
  axis equal                  % set axis to be equal (graph #3)
  p1('axis equal, axis tight','#4',x,y) % plotting the 4th graph
  axis equal, axis tight      % set axis to be equal and tight (graph #4)
function p1(a,b,x,y)  % plotting function
  figure              % new figure
  plot(x,y)           % plotting graph
  title(a)            % plotting a title
  xlabel(b)           % plotting a label for abscissa

% PLOT(X,Y) plots vector Y versus vector X.
% Various line types, plot symbols and colors may be obtained with plot(X,Y,S)
% where S is a character string made from one element from any or all the following 3 columns:
%
%            b     blue          .     point              -     solid
%            g     green         o     circle             :     dotted
%            r     red           x     x-mark             -.    dashdot
%            c     cyan          +     plus               --    dashed
%            m     magenta       *     star             (none)  no line
%            y     yellow        s     square
%            k     black         d     diamond
%            w     white         v     triangle (down)
%                                ^     triangle (up)
%                                <     triangle (left)
%                                >     triangle (right)
%                                p     pentagram
%                                h     hexagram
% plot(tn, yn, 'bx') plots blue x-mark at each data point but does not draw any line.

I. Displaying multiple plots

We give examples of codes to display two graphs in two different figures

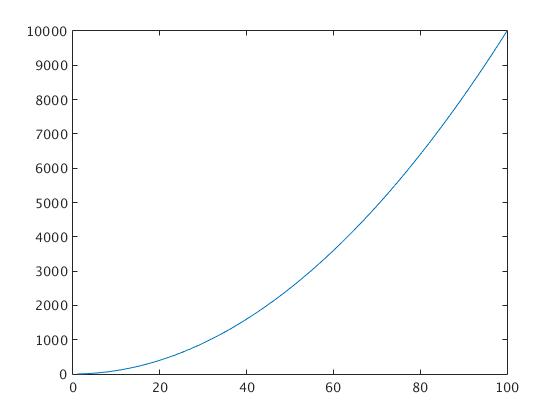
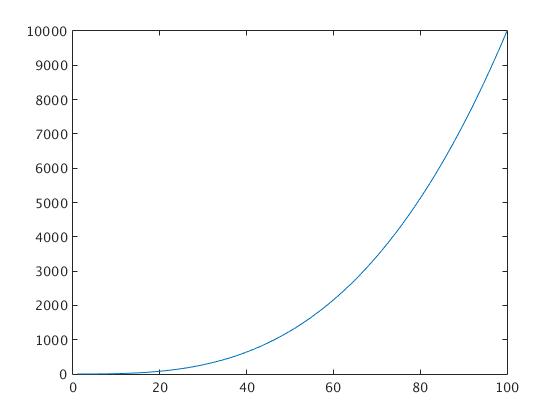
x=1:100; % making an array of x from 1 to 100
y1=x.^2; % defining and calculating y1 as x.^2 . NOTE: .^ opertator is used for element wise array manupulation
y2=(x.^3)/100; % defining and calculating y2 as (x.^3)/100
figure % opens new figure
plot(x,y1) % plots the first graph of x-y1
figure     % opens second new figure
plot(x,y2) % plots the second graph of x-y2

There is a special subroutine multigraf.m that allows one to place up to six Matlab figures on one page. THis will give you a window into which you can insert several figures produced by dfield.

Next we give examples of codes to display multiple plots on the same figure

x=1:100; % making an array of x from 1 to 100
y1=x.^2; % defining and calculating y1 as x.^2 . NOTE: .^ opertator is used for element wise array manupulation
y2=(x.^3)/100; % defining and calculating y2 as (x.^3)/100
figure     % opens new figure
plot(x,y1) % plots the first graph of x-y1
hold on
plot(x,y2) % plots the second graph of x-y2         

The code for a simple plot function in matlab is plot(independent variable, dependent variable). The independent and dependent variables can be defined either before using the plot function or within the plot function itself and must be matrices of equal sizes. Therefore,

plot([1, 2, 3, 4], [1, 2, 3, 4])

x = [1, 2, 3, 4];
y = [1, 2, 3, 4];
plot(x, y)

x = linspace(0, 2*pi);
plot(x, 2*sin(3*x)-2*cos(x))

In the above script, the independent variable is x with a range from 0 to 2π. The linspace function produces a row vector of 100 evenly spaced points between 0 and 2π. To plot multiple graphs in different windows, use the figure command between plot functions. For multiple plots in the same window, use the hold on command between plot functions or use commas between sets of independent and dependent variables within the plot function.

t1 = linspace(0, pi);
t2 = linspace(pi, 2*pi);
plot(cos(t1), sin(t1), 'k', cos(t2), sin(t2), '--k', 'LineWidth', 2)

The axis command can be used to restrict the horizontal and/or vertical range as shown in the following example.

x = linspace(-0.5, 0.5);
plot(x, exp(10*x), 'k', 'LineWidth', 2)
xlabel('x');
ylabel('exp(10*x)');

plot(x, exp(10*x), 'k', 'LineWidth', 2)
xlabel('x');
ylabel('exp(10*x)')
axis([-0.5, 0.5, 0, 10]);

The simplest way to plot a downward sine function is to translate the entire function by ±π along the x-axis.

x = -5:0.1:5;
              plot(x, sin(x + pi))

Plotting data in Matlab is simple. For example, to plot two functions
sin x and cos x on the interval 0<x<10, type in:

 t = 0:.1:10; 
 x=cos(t); y=sin(2*t);
 plot(t,x,t,y)

matlab lets you edit and annotate a graph directly from the window. For example, you can go to Tools> Edit Plot, then double-click the plot. A menu should open up that will allow you to add x and y axis labels, change the range of the x-y axes; add a title to the plot, and so on.

You can change axis label fonts, the line thickness and color, the background, and so on – usually by double-clicking what you want to change and then using the pop-up editor. You can export figures in many different formats from the File> Save As menu – and you can also print your plot directly. Play with the figure for yourself to see what you can do. Here are some basic commands and their functions:

>> xlabel     % input your horizontal axis (abscissa) title here
>> ylabel     % input your vertical axis (ordinate) title here
>> title        % input your title here
>> legent    % "my first curve title", "my second curve title" , and so on
>> grid on  % turns grid lines on
>> figure    % opens the plot in a new figure
>> axis off  % to turn of the axis
>> axis on   to turn axis back (they are on by default)

All stylistic features of graphs can be edited in the graph itself by clicking on the insert tab on the graph window:

To plot multiple lines on the same plot you can use

 clear all
     for i=1:101 t(i) = 2*pi*(i-1)/100; end
     x = cos(t);
  plot(t,x)

 hold on
 y = sin(2*t);
 plot(x,y)     

 clear all
        for i=1:101 t(i) = 2*pi*(i-1)/100; end          
            x(1,:) = cos(t);
            x(2,:) = sin(2*t);
            x(3,:) = sin(3*t);
        plot(t,x)

Here, x is a matrix. The notation x(1,:) fills the first row of x,
x(2,:) fills the second, and so on. The colon : ensures that the
number of columns is equal to the number of terms in the vector x. If
you prefer, you could accomplish the same calculation in a loop:

 for i=1:length(x) y(1,i) = sin(x(i)); y(2,i) = sin(2*x(i)); y(3,i) = sin(3*x(i)); end
 plot(x,y)

Notice that when you make a new plot, it always wipes out the old
one. If you want to create a new plot without over-writing old ones, you can use

 figure
 plot(x,y)

The ‘figure’ command will open a new window and will assign a new
number to it (in this case, figure 2). If you want to go back and
re-plot an earlier figure you can use

 figure(1)
 plot(x,y)

If you like, you can display multiple plots in the same figure, by
typing

 newaxes = axes;
 plot(x,y)

 yetmoreaxes = axes;
 plot(x,y)

 axes(newaxes);
 plot(x,y)

Doing parametric plots is easy. For example, try

 for i=1:101 t(i) = 2*pi*(i-1)/100; end
 x = sin(t); y = cos(t);
 plot(x,y)

 for i=1:101
		    theta(i) = -pi + 2*pi*(i-1)/100;
		    rho(i) = 2*sin(5*theta(i));
	end
	figure
		    polar(theta,rho)

you get
.... five.jpg

 for i =1:51 x(i) = (i-1)/50; y(i)=x(i); end
		    z = transpose(sin(2*pi*y))*sin(2*pi*x);
	figure
		    contourf(x,y,z)

The first two lines of this sequence should be familiar: they create row vectors of equally spaced points.
The third needs some explanation – this operation constructs a matrix z, whose rows and columns satisfy
z(i,j) = sin(2*pi*y(i)) * sin(2*pi*x(j)) for each value of x(i) and y(j).
If you like, you can change the number of contour levels

>>contourf(x,y,z,15)
.... contour15.jpg
You can also plot this data as a 3D surface using

>> surface(x,y,z)
... survace.jpg

The result will look a bit strange, but you can click on the ‘rotation 3D’ button (the little box with a
circular arrow around it ) near the top of the figure window, and then rotate the view in the figure with
your mouse to make it look more sensible.
.... surface2.jpg