Complex numbers were introduced by the Italian famous gambler and mathematician Gerolamo Cardano (1501--1576) in
1545 while he found the explicit formula for all three roots of a cube equation. Many mathematicians contributed to
the full development of complex numbers. The rules for addition, subtraction, multiplication, and division of complex
numbers were developed by the Italian mathematician Rafael Bombelli (baptised on 20 January 1526; died 1572).
The notations 1 and i for unit vectors in horizontal positive direction and
vertical pozitive direction, respectively, were introduced by Leonhard Euler (1707--1783) who visualized complex numbers
as points with rectangular coordinates, but did not give a satisfactory foundation for complex numbers theory. He also
suggested to drop the unit vector 1 in presenting vectors on the plane. It was Carl Friedrich Gauss (1777--1855) who introduced the term complex number. The more or less full history of discovery of complex numbers
can be found on the web:
Hiistory
There is no universal notation for a unit vector in a positive vertical direction on the complex plane ℂ.
Complex numbers, whose set is denoted by ℂ, have the form
\( z = x+{\bf i}y, \) or \( z = x+{\bf j}y, \)
where i, also denoted as j, is the imaginary unit
vector on the complex plane ℂ, in a positive vertical direction; so
j² = -1. matlab utelizes both standard notations
for such unit vector on complex plane: 1i and 1j. The real and imaginary parts of z are denoted as Re(z) or ℜz and Im(z) or ℑz, respectively. Unless redefined otherwise, matlab variables i as well as j denote
the imaginary unit. To introduce a complex number with real part x and
imaginary part y, one can just write x+i*y or x+1j*y; as an alternative, one can
use the command complex: complex(x,y).
Another way to define complex numbers:
matlab can handle complex numbers. Try the following
So we get the real part, the imaginary part, and the complex conjugate
\( \overline{z} = x-{\bf j}y , \)
which is also denoted in physics as
\( \overline{z} = z^{\dagger} . \) We can also get
for free its argument (angle in polar form) and the magnitude (length):
The trigonometric representations of a complex number
z is due to the Euler formula:
\[
z = \rho \,e^{{\bf j}\theta} = \rho \left( \cos\theta + {\bf j} \sin\theta \right) ,
\]
where
\( \rho = \sqrt{x^2 + y^2} \) is the modulus of the complex number (it can be obtained
by setting abs(z)) while
\( \theta \) is its argument, that is the angle between the
x axis and the straight line issuing from the origin and passing from the
point of coordinate (x, y) in the complex plane
\( \theta \) can be found by typing
angle: angle(z).
The graphical polar representation of one or more complex numbers
compass can be obtained through the command compass(z), where z is either
a single complex number or a vector whose components are complex
numbers. For instance, by typing
You can even do nasty things like
If you have not already done so, use
matlab to calculate
>> sin(pi)
ans =
1.2246e-16
The answer, of course, should be zero, but matlab returns a small, but
finite, number. This is because matlab stores floating point numbers
as sequences of binary digits with a finite length. Obviously, it is
impossible to store the exact value of "pi" in this way.
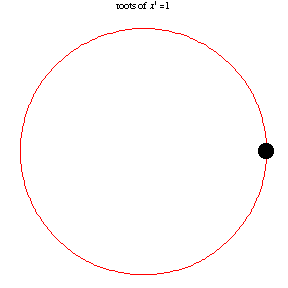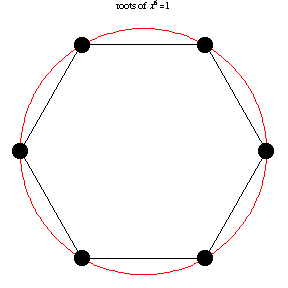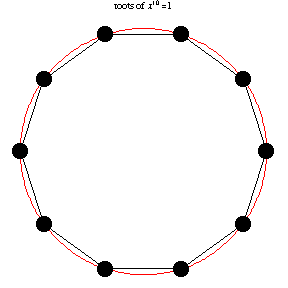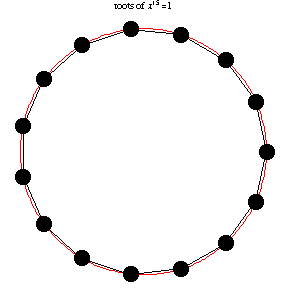
The following animation, developed by Wolfram Research, shows all
n-th roots of unity
\( \left( 1 \right)^{1/n} = \sqrt[n]{1} \) for different positive integer values of
n:
\( n=1,2,\ldots , 14 . \)