Mathematical models utilized to describe population growth evolved, undergoing several modifications after Malthus’ model (1798).
One of the most important and well known models was proposed by the Belgium sociologist P. F. Verhulst (1838).
In this model, it is assumed that all populations are prone to suffer natural inhibitions in their growths, with a tendency to reach a steady limit value as time increases. Another important proposal was developed by Montroll (1971),
which consists of a general model, that translates the asymptotic growth of a variable taking into account the position of the inflection point of the curve.
Growth or decay is a common occurrence in many systems ranging from biology to economics. Since mathematical language is more concise and less ambiguous than any natural language, the biological models were revised leading to the proposal of a variety of growth curves and the theoretical frameworks that lay behind them. Due to environmental trends and fluctuation, probably no biologist believes that one equation would suit all growth processes. This situation is completely different from those that we observe in physics, where usually only one law is used. For instance, modeling of the fall of a body in a vacuum requires only one of Newton's laws.
In many systems, growth patterns are ultimately subjected to some form of limitation.
In practice, we usually observe a set of measured values Yt,
at some time sequence { t }, called a time series. Modeling these observations means finding a curve P(t) that is closed to the time series. For example, to model a US population growth, we deal with an equally spaced time series, based on the census, conducted every ten years.
In this section, we discuss some simple models that are expressed solely in terms of differential equations of the first order that ignore random fluctuations in the population. Such models are referred to as deterministic and they are written as
\[
\frac{{\text d}P}{{\text d}t} = r(t,P) ,
\]
where
P(
t) is the size of population at time
t and
r is the rate of change.
A number of curve models have been developed to describe and predict such behaviors. For example, Kiviste (1988) described 75 of them in a two-volume monograph. See also the comprehensive work by Boris Zeide. There are two basic trends in population models: either autonomous differential equations or separable equations:
\[
\frac{{\text d}P}{{\text d}t} = r(P) \qquad\mbox{or} \qquad \frac{{\text d}P}{{\text d}t} = \zeta (t)\,f(P) .
\]
In many practical cases, these two approaches lead to the same population curve. Also, with different parametrizations, the same model may be written in distinct (equivalent) ways. Mathematical models to describe growth phenomena can be useful in many fields of interest including biology, ecology, medicine, or economics.
Another important example gives a tumor growth, and, in particular, cancer growth. Although cancer as well as many other tumor diseases are uncontrolled cell proliferation, developing their models may contribute to our more insightful description of changing phenomena.
Malthus and Doomsday models of population growth
With developing mathematical methods, biologists started in the late 18th century to use these techniques in population modeling in order to understand the dynamics of growing and shrinking populations of living organisms.
Thomas Malthus (1766--1834) was one of the first to note that populations grow with a geometric pattern (dP/dt = r P) while contemplating the fate of humankind. The Malthus model leads to exponential (unbounded) growth, which is clearly not viable in the long-term run:
\[
\frac{{\text d}P}{{\text d}t} = r\,P \qquad \Longrightarrow \qquad P(t) = P(0)\, e^{r\,t} .
\]
In 1960, H. von Foerster, P.M. Mora, and L.W.Amiot proposed a Doomsday model:
\[
\frac{{\text d}N}{{\text d}t} = r\, N^{1+1/k} ,
\]
DSolve[{n'[t] == r*(n[t])^(1 + 1/k), n[0] == a}, n[t], t]
which has the solution
\[
N(t) = \frac{k^k}{\left( N(0)^{-k} k - r\,t \right)^k} .
\]
From the formula above, a very disturbing conclusion follows: there is a finite time
t =
N-k k/r at which the population size becomes infinite. Therefore, the doomsday model gives more striking prediction of future catastrophe than even Malthus could come up with.
Von Foerster and his colleagues present many examples of accepted models of physical systems with singularities: pressure as a function of velocity approaching the speed of sound, current approaching breakdown voltage in gaseous conduction, index of refraction in optical absorption bands, and magnetic susceptibility at Curie temperature in ferromagnetism. It is reasonable to expect a singular behavior of a social structure subjected to extreme overpopulation. Nevertheless, the doomsday model provides a remarkably good fit of practical examples for certain time intervals.
Example:
In 1798, the English clergyman, professor, and political economist Thomas R. Malthus published anonymously a pamphlet entitled
An Essay on the Principle of Population as It Affects the Future Improvement of Society, with Remarks on the Speculations of Mr. Godwin, M. Condorcet, and Other Writers.
This pamphlet was meant to counter some of the rosier utopian views of that time on the perfectibility of human society. Malthus' counter argument was that population growth would eventually produce widespread poverty or worse. His model was
\[
\frac{{\text d}P}{{\text d}t} = r\,P(t) ,
\]
where
r is the per capita rate of increase –that is, how quickly the population grows per individual already in the population. If we assume no movement of individuals into or out of the population,
r can be assumed to be a constant because it is just a difference of birth and death rates. Of course, this is a very simple model that has the explicit solution:
\[
P(t) = P \left( t_0 \right) e^{r \left( t - t_0 \right)} .
\]
■
Another fundamental growth mode is one subjected to limitations that affect growth rates, making growth slow down over time and asymptotically strive towards a maximum value. Growth may actually continue interminably but the rate of growth approaches zero as time tends to infinity. This is well-known in many biological systems where an organism may grow quickly in its juvenile stage but then growth slows down as it reaches maturity.
Bounded growth curves can be used to model renewable energy sources since some kind of upper limit must exist even for renewable energy.
Rather in the growth process itself,
the limiting factor lies in the form of the increasing monetary, energy, or resource costs required for continued expansion. The upper limit may be high, or virtually non-existent, but the steps in development become more and more challenging to take, thus slowing the growth process. In the biological sciences, this is often seen as proportionality between growth rate and actual size or age.
Logistic model of population growth
The best example of exponential growth is seen in bacteria. Bacteria are
prokaryotes that reproduce by prokaryotic fission. This division takes about an hour for many bacterial species. If we use
E. coli bacteria, we could start with just one bacterium and have enough bacteria to cover the Earth with a 30-cm layer in just 36 hours.
Usually, we never observe such exponential growth in long time run because of limitation of resources. Therefore, the Malthus model can be used only for relatively short period of time.
■
One of the most basic and milestone models of population growth was the logistic model of population growth formulated by Pierre François Verhulst in 1838. (We don't know why Verhulst called this equation logistic, but this name is universally accepted.) An outstanding exposition of its history is given by
G. Evelyn Hutchinson (1903--1991) in his book, published in 1978.
The logistic model (\( \dot{P} = r\,P \left( 1 - P/K \right) \) ) takes the shape of a sigmoid curve and describes the growth of a population. He observed that if species are not preyed upon, its population is expected to saturate. Its solution is
\[
P(t) = \frac{K}{1 + \left( \frac{K}{P(t_0)} -1 \right) e^{-r(t- t_0 )}} , \qquad \mbox{subject to} \quad P\left( t_0 \right) < K .
\]
Here
t is the number of days since the starting day,
t0. The population size can also be written as
\[
P(t) = \frac{K}{1 + e^{b - r(t- t_0 )}} ,
\]
where
b is the fitting coefficient:
\[
b = \ln \left( \frac{K}{P(t_0)} -1 \right) .
\]
The logistic model can be also written in the form:
\[
\frac{{\text d}P}{{\text d}t} = \zeta (t)\,P(t), \qquad \zeta (t) = \frac{r \left( K- P(0) \right)}{P(0)\,e^{rt} + K - P(0)} , \quad t\ge 0.
\]
The relative growth rate (1/
P(d
P/d
t) declines linearly (no maximum) with increasing population size and reaches its zero minimum at
P =
K, the carrying capacity. The population at the inflection point (where growth rate is maximum)
\[
t_{inf} = \frac{1}{r}\, \ln \left( 1 - \frac{P}{K} \right)
\]
is exactly half the carrying capacity.
Example:
Using the actual data of US population given in the following table, we model it by the logistic equation with the
intrinsic growth rate r = 0.03 and the
carrying capacity N = 10000:
\[
\dot{P}(t) = r\,P \left( 1 - \frac{P}{K} \right) .
\]
| U.S. Population and logistic population growth |
|
Year(t)
|
Actual Population
|
Value of P(t)
|
Year(t)
|
Actual Population
|
Value of P(t)
|
|
|
(in millions)
|
|
|
(in millions)
|
|
|
1800 (0)
|
5.308
|
5.30
|
1900 (100)
|
72.212
|
79.61
|
| 1810 (10) |
7.239
|
7.11
|
1910 (110)
|
92.228
|
98.33
|
| 1820 (20) |
9.638
|
9.52
|
1920 (120)
|
106.021
|
119.08
|
| 1830 (30) |
12.866
|
12.71
|
1930 (130)
|
122.775
|
141.14
|
| 1840 (40) |
17.069
|
16.90
|
1940 (140)
|
132.164
|
163.59
|
| 1850 (50) |
23.192
|
22.38
|
1950 (150)
|
150.697
|
185.45
|
| 1860 (60) |
31.443
|
29.44
|
1960 (160)
|
179.323
|
205.82
|
| 1870 (70) |
38.558
|
38.42
|
1970 (170)
|
203,392
|
224.05
|
| 1880 (80) |
50.189
|
49.63
|
1980 (180)
|
226.545
|
239.78
|
| 1890 (90) |
62.979
|
63.33
|
1990 (190)
|
248.709
|
252.94
|
Using
Mathematica, we input the data:
census =
{{1790, 3.929}, {1800, 5.308}, {1810, 7.239}, {1820, 9.638}, {1830, 12.866},{1840, 17.069}, {1850, 23.192}, {1860, 31.443}, {1870, 38.558}, {1880, 50.189}, {1890, 62.979}, {1900, 72.212}, {1910, 92.228}, {1920, 106.021}, {1930, 122.775}, {1940, 132.164}, {1950, 150.697}, {1960, 179.323}, {1970, 203.392}, {1980, 226.545}, {1990, 248.709}};
Now we introduce the final time
tf = 1990;
and plot the data
censusgraph = ListPlot[census, AxesLabel->{"Year", "Population"}, AxesOrigin->{1790, 0}, PlotRange->{{1790, tf+5},{0, 300}}, PlotStyle-> {Black, PointSize[0.02]}]
First, we solve the logistic equation with the Bernoulli method by representing its solution as the product
P =
u v, where
u is a solution of the separable equation
\[
\dot{u} = r\,u \qquad \Longrightarrow \qquad u(t) = e^{rt} .
\]
Note that we need one solution of the above equation, but not the general solution. Then we substitute the product into the logistic equation:
\[
\dot{u} \,v + u\,\dot{v} = r\,u\,v - \frac{r}{K}\, u^2 v^2 .
\]
Since
u satisfies the homogeneous differential equation, terms containing multiple
v cancel out and we get
\[
u\,\dot{v} = - \frac{r}{K}\, u^2 v^2 \qquad \Longrightarrow \qquad \frac{{\text d} v}{v^2} = - \frac{r}{K}\, u\,{\text d}t = - \frac{r}{K}\, e^{rt}\,{\text d}t .
\]
Integration yields
\[
\frac{1}{v} = \frac{1}{K}\, e^{rt} + C ,
\]
where
C is a constant of integration. Multiplying these functions, we obtain the general solution of the logistic equation
\[
P(t) = u(t)\,v(t) = \frac{e^{rt}}{\frac{1}{K}\, e^{rt} + C} = \frac{K\,e^{rt}}{e^{rt} + C\,K} .
\]
To satisfy the initial condition, we have to choose
C accordingly:
\[
P(0) = \frac{K}{1 + C\,K}
\]
Solve[P == K/(1 + K*c), c]
{{c -> (K - P)/(K P)}}
DSolve[{P'[t] == r*P[t]*(1 - P[t]/K), P[0] == P0}, P[t], t]
{{P[t] -> (E^(r t) K P0)/(K - P0 + E^(r t) P0)}}
\[
P(t) = \frac{K\,P(0)\,e^{rt}}{P(0)\,e^{rt} + K- P(0)} = \frac{K\,P(0)}{P(0) + \left( K - P(0) \right) e^{-rt}} , \qquad K > P(0).
\]
This explicit formula contains three parameters:
P(0),
r, and
K. We use the census data at three years, by setting:
\[
P(0) = p0 = 5.308, \qquad P(-10) = 3.929 = \frac{K\,p0}{p0 + \left( K- p0 \right) z^{-1}} , \qquad P(10) = 7.239 = \frac{K\,p0}{p0 + \left( K- p0 \right) z} ,
\]
where
\( z = e^{-10r} . \) Multiplying the numerical values
P(-10) and
P(10) by corresponding denominators, we get
\[
P(-10) \left[ p0 + \left( K - p0 \right) z^{-1} \right] = K\,p0 \qquad\Longrightarrow \qquad \frac{1}{z} = \frac{1}{K - p0} \left[ \frac{K\,p0}{P(-10)} - p0 \right]
\]
and
\[
P(10) \left[ p0 + \left( K - p0 \right) z \right] = K\,p0 \qquad\Longrightarrow \qquad z = \frac{1}{K - p0} \left[ \frac{K\,p0}{P(10)} - p0 \right] .
\]
Now we eliminate
z from these two equations to obtain a single quadratic equation to determine the numerical value of
K:
\[
p0^2 \left[ \frac{K}{P(-10)} - 1 \right] \left[ \frac{K}{P(10)} - 1 \right] = \left( K- p0 \right)^2 .
\]
One of its solution is trivial:
K = 0, another one is
\[
K = \left( \frac{1}{P(-10)} + \frac{1}{P(10)} - \frac{2}{p0} \right)
\left[ \frac{1}{P(-10)\,P(10)} - \frac{1}{p0^2} \right]^{-1} .
\]
If one of these multiples is negative, then there does not exist a logistic curve that goes through three sequential points, as it is our case. Therefore, we need to modify the values of two points
P(-10) ≈ 4.175 and
P(10) ≈ 7.3 so that logistic curve will be close to actual data.
We solve this equation with Mathematica:
p0 = 5.308;
NSolve[p0^2 *(K/3.929 - 1)*(K/7.239 - 1) == (K - p0)^2, K]
{{K -> 0. + 0. I}, {K -> 6.65765}}
To find the value of
r, we apply the logarithm to the equation
\[
e^{10r} = \frac{p0}{K-p0} \left[ \frac{K}{P(-10)} -1 \right] = \frac{5.308}{6.65765 - 5.308} \left[ \frac{6.65765}{3,929} -1 \right] \approx
\]
K = 6.65765;
r = (1/10)*Log[p0/(K - p0)*(K/3.929 - 1)]
0.100479
Now we plot the logistic function along with census data.
 Logistic model and the actual US population.
Logistic model and the actual US population.
|
census = {{1790, 3.929}, {1800, 5.308}, {1810, 7.239}, {1820,
9.638}, {1830, 12.866}, {1840, 17.069}, {1850, 23.192}, {1860,
31.443}, {1870, 38.558}, {1880, 50.189}, {1890, 62.979}, {1900,
72.212}, {1910, 92.228}, {1920, 106.021}, {1930, 122.775}, {1940,
132.164}, {1950, 150.697}, {1960, 179.323}, {1970,
203.392}, {1980, 226.545}, {1990, 248.709}};
censusgraph =
ListPlot[census, AxesLabel -> {"Year", "Population"},
AxesOrigin -> {1790, 0}, PlotRange -> {{1790, 1995}, {0, 300}},
PlotStyle -> {Black, PointSize[0.02]}];
r = 0.03; y0 = 5.308;
lineplot =
Plot[0.159/(0.00053 + 0.02947 Exp[-0.03*(t - 1790)]), {t, 1790,
1950}];
Show[censusgraph, lineplot]
|
r=0.100479; K= 6.65765; p0=5.308;
P[t_] = K*p0/(p0 +(K-p0)*Exp[-r*(t-1800)])
logistic = Plot[P[t], {t,1800,1950}];
Show[logistic,censusgraph]
p0 = Graphics[{PointSize[Large], Pink, Point[{0, 5.3}]}];
p1 = Graphics[{PointSize[Large], Pink, Point[{10, 7.24}]}];
p2 = Graphics[{PointSize[Large], Pink, Point[{20, 9.64}]}];
p3 = Graphics[{PointSize[Large], Pink, Point[{30, 12.68}]}];
p4 = Graphics[{PointSize[Large], Pink, Point[{40, 17.06}]}];
p5 = Graphics[{PointSize[Large], Pink, Point[{50, 23.19}]}];
p6 = Graphics[{PointSize[Large], Pink, Point[{60, 31.44}]}];
p7 = Graphics[{PointSize[Large], Pink, Point[{70, 38.56}]}];
p8 = Graphics[{PointSize[Large], Pink, Point[{80, 50.19}]}];
p9 = Graphics[{PointSize[Large], Pink, Point[{90, 62.98}]}];
p10 = Graphics[{PointSize[Large], Pink, Point[{100, 76.21}]}];
p11 = Graphics[{PointSize[Large], Pink, Point[{110, 92.23}]}];
p12 = Graphics[{PointSize[Large], Pink, Point[{120, 106.02}]}];
p13 = Graphics[{PointSize[Large], Pink, Point[{130, 123.2}]}];
p14 = Graphics[{PointSize[Large], Pink, Point[{140, 132.16}]}];
p15 = Graphics[{PointSize[Large], Pink, Point[{150, 151.33}]}];
r = 0.031476; K = 10000; P0 = 5.3; c = (K - P0)/P0;
P[t_] = K*P0/((K - P0)*Exp[-r*t] + P0)
Show[plot, p0, p1, p2, p3, p4, p5, p6, p7, p8, p8, p9, p10, p11, p12, \
p13, p14, p15]
■
Since that time, there has been made substantial progress in developing mathematical population models.
Obviously, we cannot discuss and analyze a huge variety of population models. Instead, we present some famous models involving one ordinary differential equation. More complicated cases involving interaction of spices require a usage of system of differential equations, and this topic is covered in the second part of the tutorial.
Example:
Incorporating predation into the logistic equation may be done with the following differential equation
\[
\frac{{\text d}P}{{\text d}t} = r\,P \left( 1 - \frac{P}{N} \right) - \frac{a\,P^2}{b + P^2} ,
\]
where
P =
P(
t) is the population size at time
t, and coefficients
r,
N,
a, and
b are some positive constants. While the logistic equation is an example of the
Bernoulli equation, the above differential equation is not, but it is a
separable one. However, separation of variables leads to a very complicated integral
\[
\frac{{\text d}P}{r\,P \left( 1 - \frac{P}{N} \right) - \frac{a\,P^2}{b + P^2}} = {\text d}t .
\]
Instead, we apply
NDSolve for numerical approximations. First, we set some numerical values (
r=1/20,
N=1/2,
a=1/10, and
b=3), and then apply
Mathematica.

 Direction field with four solutions
Direction field with four solutions
|
field = VectorPlot[{1, P/20*(1 - P/2) - 0.1*P^2/(3 + P^2)}, {t, 0,
50}, {P, 0, 5}, VectorScale -> {0.05, 0.8, 1 &},
VectorStyle -> Black, FrameStyle -> Gray, Background -> LightGray,
FrameLabel -> {t, P}, PlotLegends -> {"time", "Population"},
DisplayFunction -> Identity];
n1 = NDSolve[{P'[t] == P[t]/20 *(1-P[t]/2)-0.1*P[t]^2 /(3+P[t]^2), P[0] == 0.2}, P[t], {t,0,50}];
n2 = NDSolve[{P;'[t] == P[t]/20 *(1-P[t]/2)-0.1*P[t]^2 /(3+P[t]^2), P[0] == 1}, P[t], {t,0,50}]
n3 = NDSolve[{P'[t] == P[t]/20 *(1-P[t]/2)-0.1*P[t]^2 /(3+P[t]^2), P[0] == 3}, P[t], {t,0,50}];
n4 = NDSolve[{P'[t] == P[t]/20 *(1-P[t]/2)-0.1*P[t]^2 /(3+P[t]^2), P[0] == 4}, P[t], {t,0,50}];
solplot = Plot[Evaluate[P[t]/.{n1,n2,n3,n4}], {t,0,50}, PlotStyle->Thickness[0.01]];
Show[solplot,field]
|
The same graphs can be obtained using command
Map.
numsol2 =
Map[NDSolve[{P'[t] == P[t]/20*(1 - P[t]/2) - 0.2*P[t]^2/(3 + P[t]^2),
P[0] == #}, P[t], {t, 0, 50}] &, {0.2, 1, 3, 4}];
solplot2 =
Plot[Evaluate[P[t] /. numsol2], {t, 0, 10},
PlotStyle -> Thickness[0.01], DisplayFunction -> Identity]
The slope function
\[
\frac{1}{20}\,P \left( 1 - \frac{P}{2} \right) - \frac{P^2}{10\left( 3 + P^2 \right)}
\]
has two critical points:
P0=0 (unstable) and
P*=1 (asymptotically stable).
■
The following two population models mimic features of asexual and sexual reproduction. The asexual reproduction model is of the form:
\[
\frac{{\text d} x}{{\text d} t} = f(x;a) = a \, x \left( 1 - x \right) - x .
\]
The sexual reproduction model is of the form:
\[
\frac{{\text d} x}{{\text d} t} = g(x;a) = a \, x^2 \left( 1 - x \right) - x .
\]
We plot direction fields for these two differential equations.
StreamPlot[{1, 3*x*(1 - x) - x}, {t, 0, 3}, {x, -1, 2},
FrameLabel -> {t, x}, MeshStyle -> {Thick}, PlotTheme -> "Business"]
StreamPlot[{1, 0.3*x*(1 - x) - x}, {t, 0, 3}, {x, -1, 2},
FrameLabel -> {t, x}, MeshStyle -> {Thick}, PlotTheme -> "Business"]
StreamPlot[{1, 3*x*x*(1 - x) - x}, {t, 0, 3}, {x, -3, 3},
FrameLabel -> {t, x}, MeshStyle -> {Thick}, PlotTheme -> "Web"]
StreamPlot[{1, 10*x*x*(1 - x) - x}, {t, 0, 3}, {x, -0.4, 1.2},
FrameLabel -> {t, x}, MeshStyle -> {Thick}, PlotTheme -> "Web"]
 Direction field for slope f with 2 equilibria.
Direction field for slope f with 2 equilibria.
|
 Direction field for slope f with 1 equilibrium.
Direction field for slope f with 1 equilibrium.
|
 Direction field for slope g with 1 real and 2 complex equilibria.
Direction field for slope g with 1 real and 2 complex equilibria.
|
 Direction field for slope g with 3 equilibria.
Direction field for slope g with 3 equilibria.
|
The above direction field plots allow us to determine the behavior of solutions near critical points; some of them are asymptotically stable, some only semi-stable, and others are unstable.
In each case, the variable
x represents a scaled population size and the parameter 𝑎 is assumed to be positive. Both slope functions have the critical point
x=0. However, the function
f has an additional
equilibrium point x=1-1/ 𝑎, while the function
g may have two more equilibrium points:
\[
x_{\pm}^{\ast} = \frac{a \pm \sqrt{a} \,\sqrt{a-4}}{2a} = \frac{1 \pm \sqrt{1- 4/a}}{2} .
\]
So we see that the slope function
f has the
bifurcation point 𝑎=1, but the slope function
g has another bifurcation point 𝑎=4. Their derivatives are
\[
\begin{split}
f' (x) &= a(1-2x) -1 \qquad \Longrightarrow\qquad f' (1-1/a) = 1-1/a , \\
g' (x) &= 2ax -3ax^2 -1 \qquad \Longrightarrow\qquad g' \left( x_{\pm}^{\ast} \right) = \frac{1}{2} \left( 4 \pm \sqrt{a}\,\sqrt{a-4} -a \right) .
\end{split}
\]
If 𝑎>1, then the derivative of
f is positive and the
critical point 1-1/𝑎 is a source (unstable). However, for 𝑎<1, the critical point is a sink (stable).
The slope function g(x) has two critical points, and the derivative at point \( x_{-}^{\ast} \) is negative for 𝑎>4; therefore, this point is asymptotically stable. The derivative of g(x) at another critical point \( x_{+}^{\ast} \) is positive for 𝑎>4. On the other hand, these two critical points disappear for 𝑎<4. So the point 𝑎=4 is a saddle-node bifurcation point.
■
Dynamics of a harvested population
Consider the dynamics of a harvested population for the logistic equation
\[
\frac{{\text d} P}{{\text d} t} = r \, P \left( 1 - \frac{P}{N} \right) - h(P) ,
\]
where
r,
N > 0, and where
h(P) is the harvesting rate. We consider several important cases starting with a constant harvesting.
The two simplest harvesting models are constant harvesting rate and proportional harvesting rate. We start with the former.
Suppose \( h(P) = h_0 \) is a constant. Then the slope function becomes
\[
f(P) = r \, P \left( 1 - \frac{P}{K} \right) - h_0 .
\]
Setting its derivative to zero, we get
\( P = \frac{1}{2}\, K . \) The function
f(P) is a downward-opening parabola whose maximum value is
\( f(K/2) = rK/4 - h_0 . \) Thus, if
\( h_0 > rK/4 , \) the harvesting rate is too large and the population always shrinks. A saddle-node bifurcation occurs at this value of
h0, and for larger harvesting rates, there are fixed points at
\[
P_{\pm} = \frac{1}{2}\, K \pm \frac{1}{2}\, K\,\sqrt{1- \frac{4h_0}{rK}} , \qquad \mbox{if }\quad rK \ge 4h_0 ,
\]
with
P- unstable and
P+ stable. When
r K < 4
h0, there are no real critical points, as the following direction fields support.
 Direction field for slope f with no equilibrium.
Direction field for slope f with no equilibrium.
|
 Direction field for slope f with 2 equilibria.
Direction field for slope f with 2 equilibria.
|
StreamPlot[{1, 1*x*(1 - x) - 1}, {t, 0, 3}, {x, -1, 2},
FrameLabel -> {t, P}, MeshStyle -> {Thick}, PlotTheme -> "Business"]
StreamPlot[{1, 5*x*(1 - x) - 1}, {t, 0, 3}, {x, -0.4, 1.2},
FrameLabel -> {t, P}, MeshStyle -> {Thick}, PlotTheme -> "Web"]
|
By rescaling the population
u = P/K, time
\( \tau = r\,t , \) and harvesting rate
\( h = h_0 /rK , \) we arrive at the equation
\[
\dot{u} = u \left( 1 - u \right) - h .
\]
The critical harvesting rate is then
\( h_c = 1/4 . \)
The proportional harvesting model is, after non-dimensionalization, of the form:
\[
\dot{u} = u \left( 1 - u \right) - h\,u .
\]
 Logistic model with periodic harvesting.
Logistic model with periodic harvesting.
|
T = 6.0; (* time interval length *)
ER = 8/3.; (* extraction rate *)
L = 16; (* carrying capacity *)
k = 1/3; (* exponential rate *)
b = 2.; (* low threshold *)
y1[1] = 15.; (* initial population *)
nT = 3; (* number of time cycles *)
Do[
soln1[i] =
DSolve[{y'[x] == k y[x] (1 - y[x]/L) - ER,
y[(2 i - 2) T] == y1[i]}, y[x], x] // Quiet // Flatten;
y2[i] = y[x] /. soln1[i] /. x -> T (2 i - 1);
soln2[i] =
DSolve[{y'[x] == k y[x] (1 - y[x]/L), y[(2 i - 1) T] == y2[i]},
y[x], x] // Quiet // Chop // Flatten;
y1[i + 1] = y[x] /. soln2[i] /. x -> T (2 i);
, {i, 1, nT}];
mytable =
Table[{{y[x] /. soln1[i], (2 i - 2) T <= x < (2 i - 1) T}, {y[x] /.
soln2[i], (2 i - 1) T <= x < (2 i) T}}, {i, 1, nT}];
myfun[x_] = Piecewise[Partition[Flatten[mytable], 2]];
Plot[{b, L, myfun[x]}, {x, 0, nT 2 T},
PlotRange -> {{0, nT 2 T}, {0.1, 1.1 L}}, Frame -> True,
PlotStyle -> {Dashing[0.02], Dashing[0.02], Automatic},
FrameTicks -> {T Range[0, 2 nT], Automatic, None, None},
AxesOrigin -> {0, 0}]
|
Rational model for harvesting
One defect of the constant harvesting rate model is that P = 0 is not a fixed point. To
remedy this, consider the following model for the harvesting rate:
\[
h(p) = \frac{a\, p^2}{p^2 + b^2} ,
\]
where 𝑎 and
b are positive constants. We can rescale (
N,
t) to (
n,τ) such that
\[
\frac{{\text d} n}{{\text d} \tau} = \gamma \, n \left( 1- \frac{n}{c} \right) - \frac{n^2}{n^2 +1} ,
\]
where γ and
c are positive constants. To examine the denominator of
h(p), we must take
P = b n. Dividing both sides of
\( \dot{P} = f(P) \) by 𝑎, we obtain
\[
\frac{b}{a}\,\frac{{\text d} P}{{\text d} t} = \frac{rb}{a} \, n \left( 1- \frac{b}{N}\, n \right) - \frac{n^2}{n^2 +1} ,
\]
from which we glean τ = 𝑎
t/b, γ =
rb/𝑎, and
c =
N/b. Now we examine the scaled population model
\[
\frac{{\text d} n}{{\text d} \tau} = g(n) = n \left[ \gamma \left( 1- \frac{n}{c} \right) - \frac{n}{n^2 +1} \right] .
\]
 Direction field for rational harvesting.
Direction field for rational harvesting.
|
StreamPlot[{1, 2*x*(1 - x) - x*x/(1 + x*x)}, {t, 0, 3}, {x, -0.4, 1},
FrameLabel -> {t, P},
StreamStyle -> Arrowheads[{{0.03, Automatic}}],
MeshShading -> {Red, None}]
|
There is an unstable fixed point at
n = 0, where
g'(0) = γ > 0. The other fixed points occur when the term in the brackets vanishes. We seek the intersection of the harvesting function
\( h(n) = n/(n^2 + 1) \) with a two-parameter family of straight lines, given by
\( y(n) = \gamma \left( 1- n/c \right) . \) The
n-intercept is
c and the
y-intercept is γ. Provided
c >
c* is large enough, there are two bifurcations as a function of γ, which we call
\( \gamma_{\pm} (c) . \)
Both bifurcations are of the saddle-node type. We determine the curves \( \gamma_{\pm} (c) \) by requiring that h(n) is tangent to y(n), which gives two equations:
\begin{align*}
h(n) &= \frac{n}{n^2 +1} = \gamma \left( 1- \frac{n}{c} \right) = y(n) ,
\\
h' (n) &= \frac{1- n^2}{\left( n^2 +1 \right)^2} = - \frac{\gamma}{c} = y' (n) .
\end{align*}
Together, these give γ(
c) parametrically, i.e. as
\[
\gamma (n) = \frac{2n^3}{\left( n^2 +1 \right)^2} , \qquad c(n) = \frac{2n^3}{n^2 -1} .
\]

|
ParametricPlot[{2*n^3/(n^2 - 1), 2*n^3/(n^2 + 1)^2}, {n, -0.6, 0.6},
Axes -> False, PlotStyle -> {Thickness[0.01]},
PlotLabel -> "Bifurcation Diagram"]
|
Since
h(
n) is maximized for
n = 1, where
\( h(1) = \frac{1}{2} , \) there is no bifurcation occurring at value
n < 1. If we plot γ(
c) versus
c(
n) over the allowed range of
n, we obtain the phase diagram. The cusp occurs at
\( \left( c^{\ast} , \gamma^{\ast} \right) , \) and is determined by the requirement that the two bifurcations coincide. This supplies a third condition, namely that the second derivative is zero:
\[
h'' (n) = \frac{2n \left( n^2 -3 \right)}{\left( n^2 +1 \right)^3} = 0 .
\]
Hence,
\( n = \sqrt{3} , \) which gives
\( c^{\ast} = 3\sqrt{3} \quad\mbox{and} \quad \gamma^{\ast} = 3\sqrt{3} /8 . \) For
c <
c*, here are no bifurcations at any value of γ.
Population model with a threshold
Suppose that when the population of species falls below a certain level (called threshold, the species cannot sustain itself, but otherwise, the population follows logistic growth. To describe this situation mathematically, we introduce the differential equation
\[
\frac{{\text d}P}{{\text d}t} = -r \left( 1 - \frac{P}{A} \right) \left( 1 - \frac{P}{B} \right) P,
\]
where 0 <
A <
B. The equilibrium solutions for this differential equation are
P = 0,
P =
A, and
P =
B. To understand the dynamics of the equation, we plot the phase portrait and pahe line:
 Bifurcation diagram.
Bifurcation diagram.
|
StreamPlot[{1, 3*x*(1 - x)*(2 - x)}, {t, 0, 3}, {x, -0.4, 3},
FrameLabel -> {t, P},
StreamStyle -> Arrowheads[{{0.03, Automatic}}],
MeshShading -> {Red, None}]
|
In 1825, the British self-educated mathematician and actuary
Benjamin Gompertz (1779---1865) introduced a demographic
model that now bears his name.
\[
\frac{{\text d}N}{{\text d}t} = r\,N(t)\,\ln \left( \frac{K}{N(t)} \right) ,
\]
where
N(
t) is the size of the population at time
t,
r is the growth rate, and
K is the equilibrium population size. Instead of the above differential equation written in a size-covariate form, it is also common to use the Gompertz model in nonautonomous form:
\[
\frac{{\text d}N}{{\text d}t} = \alpha \, e^{-rt}\,N(t) \qquad\Longrightarrow \qquad N(t) = N(0) \,\exp \left\{ \frac{\alpha}{r} \left( 1 - e^{-rt} \right) \right\} , \quad t\ge 0.
\]
The Gompertz model is one of the most frequently used sigmoid models fitted to growth data and other data, perhaps only second to the logistic model.
Researchers have fitted the Gompertz model to all range of possible applications from plant growth, bird growth, fish growth, and growth of other animals, to tumour growth and bacterial growth, and the literature is enormous.
Numerous parametrisation and reparametrisations of the Gompertz model can be found in the literature, though no systematic review of these and their properties have been attempted.
Benjamin's model is also known as the Gompertz theoretical law of mortality. He fitted it to the relationship between increasing death rate and age, what he referred to as “the average exhaustions of a man’s power to avoid death”, or the “portion of his remaining power to oppose destruction”. The insurance industry quickly started to use his method of projecting death risk. However, Gompertz only presented the probability density function.
It was W.M. Makeham who first stated this model in its well-known cumulative form, and thus it became known as the Gompertz--Makeham model.
Separation of variables in the Gompertz equation yields
\[
\frac{{\text d}N}{N\,\ln \left( \frac{K}{N} \right)} = r\,{\text d}t \qquad \Longrightarrow \qquad - \ln \left[ \ln \frac{K}{N} \right] = r\,t + C .
\]
Integrate[1/n/Log[K/n], n]
-Log[Log[K/n]]
From the initial condition, we get the value of
C to be
\[
- \ln \left[ \ln \frac{K}{N_0} \right] = C ,
\]
where
N0 =
N(0).
Exponentiation leads to
\[
\ln^{-1} \frac{K}{N_0} \, \ln \frac{K}{N} = e^{r\,t} \qquad \Longrightarrow \qquad \ln \left( \frac{K}{N(t)} \right) = e^{r\,t} \ln \left( \frac{K}{N_0} , \right)
\]
The same formula can be obtained upon substitution (from Thieme's book)
\[
x(t) = \ln \left( \frac{K}{N(t)} \right) \qquad \Longrightarrow \qquad \frac{{\text d}x}{{\text d}t} = -r\,x(t) .
\]
The derived formulas exhitit a combination of measurable quantities--namely the tumor size
N(
t) and its asymptotic limiting size
K--this yields a linear function of time if tumor growth. This observation plays an important role in fitting the Gompertz model to actual data. It is clear that
N = K is a globally asymptotically stable fixed point, and the Gompertz model exhibits sigmoidal growth.
Next exponentiation yields the explicit formula for the Gompertz's curve:
\[
N(t) = K \,\exp \left\{ - e^{-rt} \ln \frac{K}{N_0} \right\} .
\]
Another re-parameterisation of the Gompertz model
can also be written as the three parameter curve:
\[
\frac{{\text d}Y}{{\text d}t} = \alpha r \,e^{-r\, t} Y \qquad \Longrightarrow \qquad Y(t) = Y_{\infty} \exp \left\{ - \alpha\,e^{-r \, (t-t_0 )} \right\} ,
\]
where
\[
Y_{\infty} = K, \qquad \alpha = \ln \frac{K}{N_0} .
\]
Depending on circumstances, one may come across another version of the
Gompertz model
\[
N(t) = N(0)\,\exp \left\{ \frac{b}{c} \left( 1 - e^{-c\,t^h} \right) \right\} .
\]
Example:
Using data from URL:
https://ourworldindata.org/coronavirus/country/brazil?country=~BRA
we apply Gompertz's model
 Number of COVID-19 cases in Brazil.
Number of COVID-19 cases in Brazil.
|
|
 Number of COVID-19 deaths in Brazil.
Number of COVID-19 deaths in Brazil.
|
To fit the obtained data with the Gompertz's curve, we use a special
Mathematica command:
NonlinearModelFit[data, K*Exp[-a*Exp[-r*t]], {K, a, r}, t]
which yields the following values of parameters:
\[
K = 1.2630463902640887*10^7 , \qquad
a = 12.70849421908572, \qquad
r = 0.0145 .
\]
This allows us to build the Gompertz's curve
\[
N(t) = K\,\exp \left\{ -a\,e^{-r\,t} \right\} .
\]
Finally we plot the model along with the data.
 Modeling COVID-19 cases in Brazil.
Modeling COVID-19 cases in Brazil.
|
|
K = 1.2630463902640887*10^7; a = 12.70849421908572; r = 0.0145;
gompertz =
Plot[g[0.0145, t], {t, 0, 100}, PlotStyle -> {Thick, Orange}];
realdata =
ListPlot[data, PlotStyle -> Large,
LabelingFunction -> Callout[Automatic]];
Show[gompertz, realdata]
|
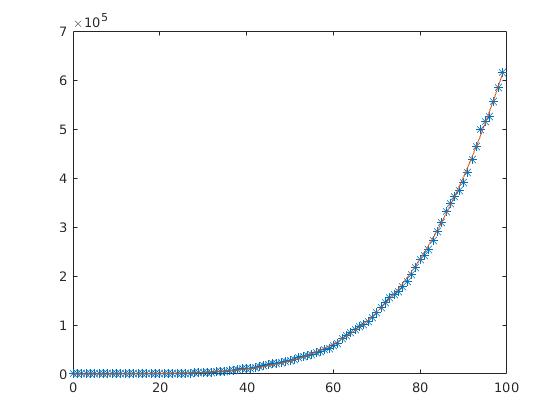
cases = [1 1 1 1 2 2 2 2 3 8 13 13 25 25 34 52 77 98 121 200 234 291 428 621 904 ...
1128 1546 1891 2201 2433 2915 3417 3904 4256 4579 5717 6836 7910 9056 10278 ...
11130 12056 13717 15927 17857 19638 20727 22169 23430 25262 28320 30425 33682 36599 38654 ...
40581 43079 45757 49492 52995 58509 61888 71886 78162 85380 91589 96559 101147 107780 ...
114715 125218 135106 145328 155939 162699 168331 177589 188974 202918 218223 233142 241080 ...
254220 271628 291579 310087 330890 347398 363211 374898 391222 411821 438238 465166 498440 ...
514849 526447 555383 584016 614941];
K= 1.2630463902640887e7
a = 12.70849421908572
r = 0.0145
t=0:1:99;
N=K*exp(-a*exp(-r*t));
figure(1)
plot(t, cases,'*',t,N)
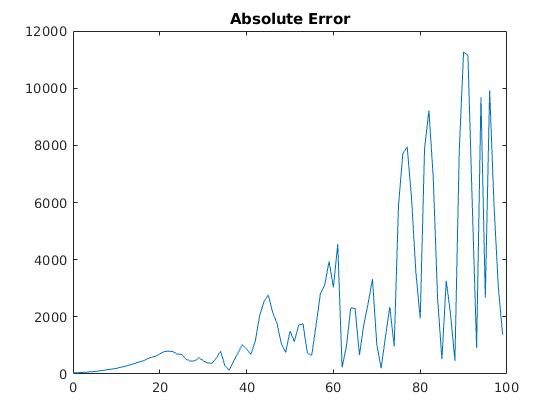
figure(2)
plot(t,abs(cases-N))
title('Absolute Error')
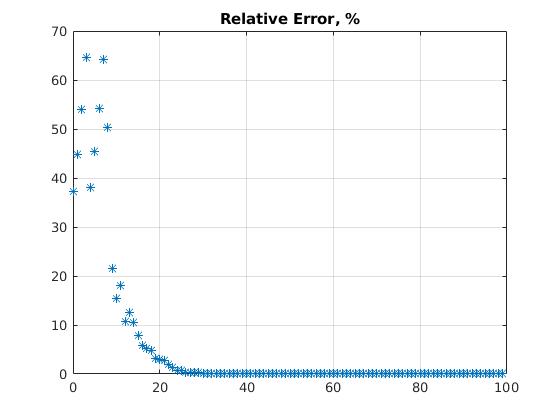
figure(3)
plot(t,abs(cases-N)./cases,'*')
title('Relative Error, %')
grid on
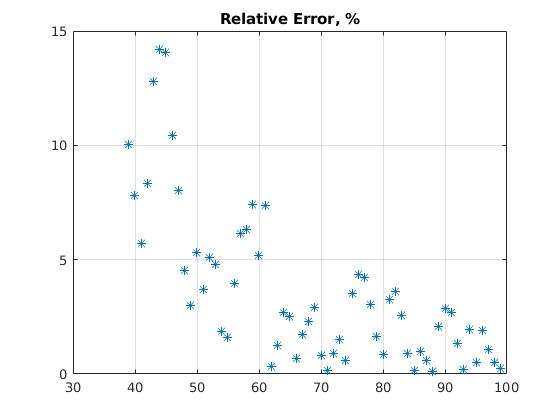
figure(4)
plot(t(40:end),100*abs(cases(40:end)-N(40:end))./cases(40:end),'*')
title('Relative Error, %')
grid on
figure(5)
plot(log(t),log(N),log(t),log(cases),'*')
title('Logarithmic Scales')
grid on
 Modeling COVID-19 cases in Brazil.
Modeling COVID-19 cases in Brazil.
|
|
 Modeling COVID-19 cases in Brazil.
Modeling COVID-19 cases in Brazil.
|
|
 Modeling COVID-19 cases in Brazil.
Modeling COVID-19 cases in Brazil.
|
 Modeling COVID-19 cases in Brazil.
Modeling COVID-19 cases in Brazil.
|
|
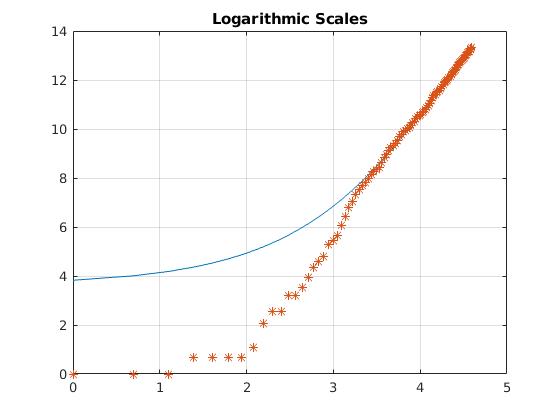 Modeling COVID-19 cases in Brazil.
Modeling COVID-19 cases in Brazil.
|
We repeat a similar procedure with the number of deeaths caused by COVID-19 in Brazil.
 Gompertz's Model of COVID-19 deaths in Brazil.
Gompertz's Model of COVID-19 deaths in Brazil.
|
|
dayssincefirstcase = {0, 1 , 2, 3, 4 , 5 , 6 , 7, 8, 9, 10, 11, 12,
13, 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25 ,
26 , 27, 28 , 29, 30 , 31 , 32 , 33 , 34 , 35 , 36 , 37 , 38 , 39 ,
40 , 41 , 42 , 43 , 44, 45, 46 , 47 , 48 , 49 , 50 , 51 , 52 ,
53, 54 , 55 , 56 , 57 , 58 , 59 , 60 , 61 , 62 , 63 , 64 , 65 ,
66 , 67 , 68 , 69 , 70 , 71 , 72 , 73, 74, 75, 76 , 77, 78 , 79,
80, 81 , 82 , 83 , 84 , 85 , 86 , 87 , 88 , 89, 90 , 91 , 92, 93,
94 , 95, 96 , 97, 98, 99, 100};
totald = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 4, 6, 11, 18, 25, 34, 46, 57, 77, 92, 114, 136, 159, 201, 241,
299, 359, 432, 486, 553, 667, 800, 941, 1056, 1124, 1223, 1328,
1532, 1736, 1924, 2141, 2347, 2462, 2575, 2741, 2906, 3313, 3670,
4016, 4205, 4543, 5017, 5466, 5901, 6329, 6750, 7025, 7321, 7921,
8536, 9146, 9897, 10627, 11123, 11519, 12400, 13149, 13993, 14817,
15633, 16118, 16792, 17971, 18859, 20047, 21048, 22013, 22666,
23473, 24512, 25598, 26754, 27878, 28834, 29314, 29937, 31199,
32548, 34021, 34021};
datad = Thread[{dayssincefirstcase, totald}];
reald = ListPlot[datad, PlotStyle -> Large,
LabelingFunction -> Callout[Automatic]];
NonlinearModelFit[datad, K*Exp[-a*Exp[-r*t]], {K, a, r}, t]
K = 128239.9181316305; a = 14.346820302208794; r = 0.024;
gompertz =
Plot[g[0.024, t], {t, 0, 100}, PlotStyle -> {Thick, Orange}];
reald =
ListPlot[datad, PlotStyle -> Large,
LabelingFunction -> Callout[Automatic]];
Show[gompertz, reald]
|
■
In 1939, the Czech scientist V. Korf proposed the following model
\[
\frac{{\text d}N}{{\text d} t} = N(0)\left( 1 + t \right)^{-\beta -1}\, N(t) , \quad t> 0,
\]
to describe the dependence of a tree's height on its width. The Korf differential equation is easy to solve by separating variables.
\[
\frac{{\text d}N}{N} = N(0)\left( 1 + t \right)^{-\beta -1}\,{\text d} t \qquad \Longrightarrow \qquad \ln N(t) = - \frac{N(0)}{\beta}\left( 1 + t \right)^{-\beta} + C .
\]
From the initial condition, we we get
\[
C = \ln N(0) + \frac{N(0)}{\beta} .
\]
This yields
\[
N(t) = N(0) \,\exp \left\{ \frac{N(0)}{\beta} \left[ 1 - \left( 1 + t \right)^{-\beta} \right] \right\} , \quad t\ge 0.
\]
 Solution of the Korf model.
Solution of the Korf model.
|
|
b = 2.3;
NN[t_] = 0.2*Exp[0.2/b*(1 - 1/(1 + t)^b)]
Plot[NN[t], {t, 0, 3}, PlotStyle -> Thick]
|
|
Another model was proposed by F.J. Richards in 1959:
\[
\frac{{\text d}R}{{\text d} t} = r\, R(t) \left[ 1 - \left( \frac{R(t)}{K} \right)^a \right] , \qquad R(0) = R_0 .
\]
His model contains four common parameters: a generalised growth rate
𝑟 setting the typical time scale of the epidemic growth process, the final capacity
K, which is the asymptotic total number of infections over the whole epidemics, the exponent 𝑎, which is introduced to measure the deviation from the symmetric S-shaped dynamics of the simple logistic curve, and one additional parameter 𝑎 ∈ [0,1].
Since the Richards equation is an example of a more general Bernoulli equation, we seek its solution in the form of the product R(t) = u(t) v(t), where
u(t) is a solution of the truncated linear equation
\[
\frac{{\text d}u}{{\text d} t} = r\, u(t) \qquad \Longrightarrow \qquad \frac{{\text d}u}{u} = r\,{\text d}t .
\]
Integration yields
\[
\ln u = r\,t \qquad \Longrightarrow \qquad u(t) = e^{r\,t} .
\]
Substituting the product
R(
t) =
u(
t)
v(
t) into the Richards equation, we obtain a separable equation for the unknown function
v(
t):
\[
u\,\dot{v} = - \frac{r}{K^a} \, v^{a+1} u^{a+1} \qquad \Longrightarrow \qquad
\frac{{\text d}v}{v^{a+1}} = - \frac{r}{K^a} \, u^{a} \,{\text d}t = - \frac{r}{K^a} \, e^{ar\,t}\, {\text d}t .
\]
Integrating both sides, we get the general solution
\[
- \frac{1}{a\,v^a} = - \frac{r}{K^a} \,\frac{1}{ar} \,e^{ar\,t} - \frac{C}{a}
\qquad \Longrightarrow \qquad v^{-a} = \frac{1}{K^a}\, e^{ar\,t} + C ,
\]
where
C is a constant of integration. From the initial condition
\( R_0 = R(0) = v(0) , \) we derive
\[
R_0^{-a} = \frac{1}{K} + C \qquad \Longrightarrow \qquad C = R_0^{-a} - K^{-a} = C .
\]
Multiplying
u and
v, we obtain the solution
\[
R(t) = u\,v = e^{rt} \left[ \frac{1}{K^a}\, e^{ar\,t} + R_0^{-a} - K^{-a} \right]^{-1/a} = \frac{K\,e^{r\,t}}{\left[ e^{ar\,t} + \left( \frac{K}{R_0} \right)^{a} -1 \right]^{1/a}}
\]
Its solution can be simplified to
\[
R(t) = \frac{K}{\left( 1 + \left[ \left( \frac{K}{R(0)} \right)^a -1 \right] e^{-rt} \right)^a} .
\]
 Solution of the Richards model.
Solution of the Richards model.
|
|
P[t_] = Exp[2*t]/(-1 + Exp[2*t*0.3] + (1/0.2)^0.3)^(10/3)
Plot[P[t], {t, 0, 8}, PlotRange -> {0, 1}, PlotStyle -> Thick]
|
|
Example:
We consider the data from Sweden:
| Coronavirus cases in Sweden |
|
Days (March 1 corresponds to 1)
|
Actual Cases: Sweden
|
Predicted Value of P(t)
|
Days (March 1 corresponds to 1)
|
Actual Cases: Sweden
|
Predicted Value of P(t)
|
|
1
|
14
|
|
61 (April 30)
|
21092
|
|
|
5
|
94
|
|
65 (May 4)
|
22721
|
|
|
9 (March 9)
|
260
|
|
69 (May 8)
|
25265
|
|
|
13 (March 13)
|
814
|
|
73 (May 12)
|
27272
|
|
|
17 (March 17)
|
1196
|
|
77 (May 16)
|
29677
|
|
|
21 (March 21)
|
1770
|
|
81 (May 20)
|
31523
|
|
|
25 (March 25)
|
2526
|
|
85 (May 24)
|
33459
|
|
|
29 (March 29)
|
3770
|
|
89 (May 28)
|
35727
|
|
|
33 (April 2)
|
5568
|
|
93 (June 1)
|
|
|
|
|
37 (April 6)
|
7206
|
|
97 (June 5)
|
0
|
|
|
41 (April 10)
|
9685
|
|
0
|
|
|
45 (April 14)
|
11445
|
|
0
|
|
|
49 (April 18)
|
13822
|
|
0
|
|
|
53 (April 22)
|
16004
|
|
0
|
|
|
57 (April 26)
|
18640
|
|
0
|
|
 Number of COVID-19 cases in Sweden.
Number of COVID-19 cases in Sweden.
|
|
sweden = {{1,15}, {5,94}, {9,260}, {13,814}, {17, 1196}, {21,1770}, {25,2526}, {29,3700}, {33, 5568}, {37,7206},{41,9685}, {45,11445}, {49,13822},{53,16004},{57,18640}, {61,21092}, {65,22721},{69,25265}, {73,27272},{77,29677},{81,31523},{85,33459}, {90,35727}};
censusgraph =
ListPlot[sweden, AxesLabel -> {"Days", "Number of COVID cases"},
AxesOrigin -> {0, 0}, PlotRange -> {{0, 90}, {0, 36000}},
PlotStyle -> {Black, PointSize[0.02]}];
|
|
Using
Mathematica we try to determine the numerical values of parameters in the Richards model.
NonlinearModelFit[sweden,
K*Exp[r*t]/(K^a + Exp[a*r*t] - 1)^(1/a), {r, a, K}, t]
 Number of COVID-19 deaths in Sweden.
Number of COVID-19 deaths in Sweden.
|
swed = {{14, 2},
{18, 10},
{22, 21},
{26, 77},
{30, 146},
{34, 353},
{38, 591},
{42, 887},
{46, 1333},
{50, 1540},
{54, 2021},
{58, 2274},
{62, 2653},
{66, 2854},
{70, 3220},
{74, 3460},
{78, 3679},
{82, 3871},
{86, 4029},
{90, 4350},
{94, 4468}};
censusgraph =
ListPlot[swed, AxesLabel -> {"Days", False},
PlotLabel -> "Number of COVID deaths in Sweden",
AxesOrigin -> {14, 0}, PlotRange -> {{10, 95}, {0, 4500}},
PlotStyle -> {Black, PointSize[0.02]}]
|
|
HN = NonlinearModelFit[sweden,
K/(1 + Exp[b - r*x])^(a), {r, b, a, K}, {x}]
because
\[
R(t) = \frac{K}{\left( 1 + e^{b-rt} \right)^a} , \qquad b = \ln \left[ \left( \frac{K}{R(0)} \right) -1\right] .
\]
■
The Weibull model is
\[
\frac{{\text d}W}{{\text d} t} = \beta\gamma \,t^{\gamma -1} \left( W_{\infty} - W \right) \qquad \Longrightarrow \qquad W(t) = W(0) \, e^{-\beta\, t^{\gamma}} + W_{\infty} \left[ 1 - e^{-\beta\, t^{\gamma}} \right] , \quad t \ge 0.
\]
DSolve[{W'[t] == beta*gamma *t^(gamma - 1) *(A - W[t]), W[0] == a},
W[t], t];
Assuming[ gamma > 0, Simplify[%]]
Example:
Let us look at the data for two countries, Italy and South Africa, that can be obtained from the official WHO web pages:
https://www.worldometers.info/coronavirus/country/italy/
https://www.worldometers.info/coronavirus/country/south-africa/
| Coronavirus cases for two countries: Italy and South Africa |
|
Days (March 1 corresponds to 1)
|
Actual Cases: Italy
|
Predicted Value of P(t)
|
Actual Cases: South Africa
|
Predicted Value of P(t)
|
|
1
|
1701
|
|
0
|
|
|
5
|
3858
|
|
1
|
|
|
9
|
9172
|
|
7
|
|
13
|
17,660
|
|
24
|
|
|
17
|
31,506
|
|
85
|
|
|
21
|
53,578
|
|
240
|
|
|
25
|
74,386
|
|
709
|
|
|
29
|
97,689
|
|
1,280
|
|
|
33 (April 2)
|
115,242
|
|
1,686
|
|
|
37 (April 6)
|
132,547
|
|
1,686
|
|
|
41 (April 10)
|
147,577
|
|
2,003
|
|
|
45 (April 14)
|
162,488
|
|
2,415
|
|
|
49 (April 18)
|
175,925
|
|
3,034
|
|
|
53 (April 22)
|
187,327
|
|
3,635
|
|
|
57 (April 26)
|
197,675
|
|
4,546
|
|
|
61 (April 30)
|
205,463
|
|
5,647
|
|
|
65 (May 4)
|
211,938
|
|
7,220
|
|
|
69 (May 8)
|
217,185
|
|
8,895
|
|
|
73 (May 12)
|
221,216
|
|
11,350
|
|
|
77 (May 16)
|
224,760
|
|
14,355
|
|
|
81 (May 20)
|
227,364
|
|
18,003
|
|
|
85 (May 24)
|
229,858
|
|
22,583
|
|
To model the data, we choose parameters: α = 0.00075, β = 23/12, and
Winf = 237,000. So we get
\[
W(t) = 237,000 \left[ 1 - e^{-0.00075 \,t^{23/12}} \right] + e^{-0.00075 \,t^{23/12}} .
\]
italy = {{1,7011}, {5,3858}, {9,9172}, {13,17660}, {17, 31506}, {17,31596}, {21,53578}, {25,74386}, {29, 97689}, {33,113242},{37,132547}, {41,147577}, {45,162488},{49,175925},{53,187327}, {57,197675}, {61,205463},{65,211938}, {65,211938},{69,217185},{73,221216},{77,224760}, {81,227364},{85,229858}}
 Weibull growth model and the actual number of COVID-19 cases in Italy.
Weibull growth model and the actual number of COVID-19 cases in Italy.
|
italy = {{1,7011}, {5,3858}, {9,9172}, {13,17660}, {17, 31506}, {17,31596}, {21,53578}, {25,74386}, {29, 97689}, {33,113242},{37,132547}, {41,147577}, {45,162488},{49,175925},{53,187327}, {57,197675}, {61,205463},{65,211938}, {65,211938},{69,217185},{73,221216},{77,224760}, {81,227364},{85,229858}};
censusgraph =
ListPlot[italy, AxesLabel -> {"Days", "Population"},
AxesOrigin -> {0, 0}, PlotRange -> {{0, 90}, {0, 237000}},
PlotStyle -> {Black, PointSize[0.02]}];
beta = 0.00075; gamma = 23/12; W0=237000;
lineplot =
Plot[ Exp[-beta*t^(gamma)] + W0*(1 - Exp[-beta*t^(gamma)]), {t, 0,
90}];
Show[censusgraph, lineplot]
|
■
\[
\frac{{\text d}W}{{\text d} t} = -bc\,t^{c-1} e^{-b\,t^c} \qquad \Longrightarrow \qquad
W(t) = W_{\infty} \left( 1 - \beta \,e^{-b\,t^c} \right) , \quad c > 1,
\]
where
b is a growth parameter for a fixed
c and
c is a shape parameter. The above equation can be written as
\[
W(t) = W_{\infty} - \left( W_{\infty} - W_0 \right) e^{-k\, t^p} .
\]
For
p < 1, this function exhibits exponential growth; and for
p > 1, sigmodal growth occurs.
The von Bertalanffy model
In 1949, the Austrian biologist
Karl Ludwig
von Bertalanffy (1901--1972) introduced the differential equation as a model for organism growth. He held positions at the University of Vienna (1934-48), the University of Ottawa (1950-54), the Mount Sinai Hospital (Los Angeles) (1955-58), the University of Alberta (1961-68), and the State University of New York (SUNY) (1969-72).
In 1934, he was habilitated by Reininger, Schlick and the zoologist Versluys for the first volume of his Theoretische Biologie. The monography postulated two essential aims of a theoretical biology, firstly to clean up the conceptual terminology of biology, and, secondly, to explain how the phenomena of life can spontaneously emerge from forces existing inside an organism. Here the organismic system represented the main problem as well as the still-to-be-formulated program of a theoretical biology. The second volume developed the research program of a dynamic morphology and applied the mathematical method to biological problems.
As a Rockefeller Fellow at the University of Chicago (1937-38), he worked with the Russian physicist Nicolaus Rashevsky. There he gave his first lecture about the General System Theory as a methodology that is valid for all sciences (1949). In 1939 he was appointed to an extraordinary professor at the University of Vienna. There Bertalanffy concentrated his research on a comparative physiology of growth. He was the first biologist who held lectures in zoology for students of medicine and an integrated course on botany and zoology. During this time he wrote an article about organisms as physical systems (1940), the summary of his biological reasoning: Problems of Life.
In 1949, Ludwig emigrated to Canada where he mainly worked on metabolism, growth, biophysics, and cancer cytology. In his biomedical research on cancer he developed, with his son Felix, the Bertalanffy-method of cancer cytodiagnosis. From the 1950's onwards he shifted his research from the biological sciences to the methodology of science, the General System Theory (GST), and cognitive psychology. Based on his humanistic world view, he developed a holistic epistemology (1966) which sharply criticized the machine metaphor of neobehaviorism (Robots).
In 1960 Ludwig was appointed a Professor of the Department of Zoology and Psychology at the University of Alberta in Edmonton (Canada). There Bertalanffy, the psychologist Royce and the philosopher Tenneysen established the Advanced Center for Theoretical Psychology that became a center for cognitive psychology over the next 30 years.
In that time his systematic theoretical approach focused on the modern world of technology and has thrown us humans out of nature and has isolated us from each other.
Bertalanffy emphasized in his later works the importance of the symbolic worlds of culture which we ourselves have created during evolution.
After his retirement, he became a Professor of the Faculty of Social Sciences at the State University of New York (SUNY). An international symposium celebrated his 70th birthday in 1971. In June 1972, he suffered a heart stroke and died a few days later, on June 12, shortly after midnight.
To sum up his life-work, Bertalanffy wrote 13 monographies, four anthologies, and over 200 articles, He was the chief editor of the Handbuch der Biologie--among many others. His themes encompassed theoretical biology and experimental physiology (Bertalanffy equations), theoretical psychology--particularly in the last two decades of his life, cancer research (Bertalanffy method of cancer cytodiagnosis), and philosophy and history of science.
No doubt, the person Bertalanffy was a very fascinating one, proud of his European background, a connoisseur of architectural drawings, Japanese woodcuts, and stamps, who loved to hear the music of Mozart and Beethoven and to become absorbed in the works of Goethe. Sometimes he puzzled his environment by sarcastic remarks, or his black sense of humor. His worldview was an old-fashioned one, however, never outdated that was deeply rooted in a humanistic ethos:
In the last resort, however, it is always a system of values, of ideas, of ideologies - choose whatever word you like - that is decisive. (1964)
Bertalanffy (1957) derived his equation from the assumptions, which he attributed to Pütter (1920), that the rate of anabolism is proportional to the surface area of an organism (or to its mass raised to the power of ⅔), while catabolism is proportional to the organism's mass.
Von Bertalanffy formulation (1957) of the equation is based on the biological principles of anabolism and catabolism, that is, growth and destruction. He derived his equation from the assumptions, which he attributed to Pütter (1920), that the rate of anabolism is proportional to the surface area of an organism (or to is mass raised to the power of ⅔), while catabolism is proportional to the organism's mass.
The Bertalanffy model is often used as a population model to study the factors that control and affect its growth. It is used to describe the populations of fish, animals, such as pigs, horses, cattle, sheep, etc.
It is also suitable for modelling tumors and infectious diseases because it is similar to the growth of individuals and populations:
\[
\frac{{\text d}P}{{\text d}t} = r \left( P^{2/3} - P/K \right) .
\]
Since the Bertalanffy equation is a Bernoully equation, we solve it by representing the solution in the form of the product of two functions: P(t) = u(t) v(t). Here u(t) is a solution of the truncated linear part:
\[
\dot{u} = - \frac{r}{K}\,u \qquad \Longrightarrow \qquad \frac{{\text d}u}{u} = -\frac{r}{K}\,{\text d}t .
\]
Its solution becomes
\[
u(t) = e^{-rt/K}
\]
because we need just one such solution but not the general one. Substitution of the product into the Bertalanffy equation, we obtain for
v(
t) the following separable differential equation:
\[
u\,\dot{v} = r\,u^{2/3} v^{2/3} \qquad \Longrightarrow \qquad \frac{{\text d}v}{v^{2/3}} = r\,u^{-1/3}{\text d}t = r\, e^{rt/(3K)} \, {\text d}t .
\]
Integration yields
\[
3\, v^{1/3} = 3K\, e^{rt/(3K)} + C ,
\]
where
C is a constant of integration. Multiplication of these functions gives the required general solution:
\[
P(t) = u(t)\,v(t) = e^{-rt/K}\left[ K\, e^{rt/(3K)} + C \right]^3
\]
From the initial condition, it follows that
\[
P(0) = \left[ K + C \right]^3 \qquad \Longrightarrow \qquad P^{1/3} (0) - K = C .
\]
Therefore, we finally get the solution for the von Bertalanffy model:
\[
P(t) = e^{-r\,t/K} \left[ K\,e^{r\,t/(3K)} - K + P(0)^{1/3} \right]^3 \.\to\ K \quad \mbox{as} \quad t\to \infty ,
\]
where
t is time,
P(0) is the population size at time
t = 0,
K is carrying capacity,
r is the intrinsic growth rate.
This model attains its inflection value 8
K/27 at
\[
t_{inf} = \frac{3K}{r}\, \ln \left[ 1 - \frac{P(0)^{1/3}}{K} \right] .
\]
P[t_] = Exp[-r*t/K]*(K*Exp[r*t/3/K] - K + P0^(1/3))^3;
Solve[P'[t] == 0, {t}]
 Graph of the Bertalanffy slope function.
Graph of the Bertalanffy slope function.
|
 Solution of the Bertalanffy model.
Solution of the Bertalanffy model.
|
|
Plot[x^(2/3) - x, {x, 0, 1}, PlotStyle -> Thick]
P[t_] = Exp[-2*t/1]*(1*Exp[2*t/3/1] - 1 + 0.1^(1/3))^3
Plot[P[t], {t, 0, 8}, PlotRange -> {0, 1}, PlotStyle -> Thick]
|
|
To capture the dynamics of harvesting a population or tumour treatment we can add a harvesting term E(t) P(t). Here, E is also considered to vary with time and represents harvesting effort. Adding this term to the Bertalanffy population model results in a new harvesting IVP,
\[
\dot{P} = a(t)\,P^{2/3} - b(t)\,P(t) - E(t)\,P(t) , \qquad P(0) = P_0 .
\]
Here 𝑎(
t),
b(
t), and
E(
t) are assumed to be known positive functions of time.
U-Bertalaffy:
\[
W(t) = K\left[ 1 - \frac{1}{3} \cdot \exp\left\{ - \frac{9k\,(t-t_0 )}{4} \right\} \right]^{3}
\]
The von Bertalanffy (1957) growth law can be written as
\[
\frac{{\text d}W}{{\text d}t} = \eta\,W^{k} - \lambda\,W ,
\]
where η and λ are constants. Once this differential equation is integrated, the von Bertalanffy growth curve becomes
\[
W(t) = W_{\infty} \left[ a - \beta\,e^{-\lambda (1-k)t} \right]^{1/(1-k)} ,
\]
where
\[
W_{\infty} = \lim_{t\to \infty} W(t) = \left( \eta / \lambda \right)^{1/(1-k)}
\]
is the limit to growth parameter, β = α/η (α is a constant of integration), λ is a growth rate parameter, 1-
k is a shape parameter, and the initial value is
\[
W(0) = \left( \frac{\eta}{\lambda} - \frac{\alpha}{\lambda} \right)^{1/(1-k)} .
\]
If
k > 1 and both η and λ are negative, the growth curve is sigmodal. von Bertalanffy determined empirically that
k = 2/3 for a wide variety animals.
Spruce Budworm population
The spruce budworm is an insect which is a serious threat to forests.
In 1978, Ludwig, Jones, and Holling published a paper in which they
proposed an ingenious model of the interaction of the insects, the
trees, and the predatory birds. They proposed that the budworm
population P obeys a logistic model modified by a predation rate:
\begin{equation} \label{E24.6}
\frac{{\text d}P(t)}{{\text d}t} = P \left( r- \alpha P - \frac{\beta\,P}{k^2 + P^2} \right) ,
%\eqno{(4.6)}$$
\end{equation}
with some positive constants
r, α,
k, and β. The
parameter β represents the predation efficiency of birds and it
is proportional to the population of birds, considered a constant in
this model. The parameter
k is proportional to the average leaf
surface area (about half of it), and it is a scaled measure of the
average foliage density. So trees with larger leaves attract more
budworms. The denominator,
\( k^2 + P^2 , \) in the last term of the
equation models the laziness of birds that go for places where food
density is high allowing them to consume much while expending minimal
energy.
The analysis of the above equation for P(t) can be
simplified by introducing dimensionless variables \( t=a\tau \) and
P = by, where \( a= k/\beta \) and b = k. Then the equation
can be written in the following form:
\begin{equation} \label{E24.6a}
\frac{dy}{d\tau} = Ry(1-Ay) - \frac{y^2}{1+y^2} ,
\end{equation}
where
\( R=rk/\beta \) and
\( A=\alpha k. \)
The above equation contains two
parameters. Its slope function has obviously one
null:
y = 0, but
other critical points are obtained by solving the equation
\begin{equation} \label{E24.6b}
R(1-Ay) = \frac{y}{1+y^2} .
\end{equation}
The first step in the analysis is to identify the equilibria (where the derivative of
y is zero) and determine their stability.
Since the slope function is positive in a neighborhood of
y = 0, this
equilibrium point is unstable. Upon multiplying both
sides of the latter equation by 1 +
y², we get the cubic equation that may have
either one real root or three real roots, depending on the values of
parameters
A and
R. The best way to do the analysis is to examine
what can occur for each value of
R as
A varies.
The interpretation of the above equation is both simple and important. Its left-hand side is per capita growth
rate of the scaled variable y (with respect to a scaled time). The right-hand side is per capita death rate
due to predation, also in scaled variables. The points where these curves intersect are nonzero equilibria for
y.
 The growth rate and predation loss rate of the scaled budworm density.
The growth rate and predation loss rate of the scaled budworm density.
Two critical points
are stable and the middle is unstable.
|
R = 0.5; A = 0.1;
a = Plot[{R*(1 - A*y), y/(1 + y*y)}, {y, 0, 10}, PlotStyle -> {Thick},
Epilog ->
Text[Style["unstable", 10, FontFamily -> Times], {2.2, -0.1}],
PlotRange -> {-0.2, 0.5}]
b = ListPlot[{{0.7, 0.465}, {2.05, 0.4}, {7.34, 0.132}},
PlotStyle -> {Large, Black}]
line1 = Line[{{0.7, 0.46}, {0.7, 0}}]
line2 = Line[{{2.05, 0.39}, {2.05, 0}}]
line3 = Line[{{7.34, 0.13}, {7.34, 0}}]
c = {Graphics[{Dashed, Red, line1}], Graphics[{Dashed, Red, line2}],
Graphics[{Dashed, Red, line3}]}
Show[a, b, c]
|
The critical values of R and A are where two roots coalesce and disappear. The bifurcation points are obtained from the following system of equations:
\[
R(1-Ay) = \frac{y}{1+y^2} \qquad\mbox{and}\qquad \frac{{\text d}}{{\text d}y} \,R(1-Ay) = -RA = \frac{{\text d}}{{\text d}y} \,\frac{y}{1+y^2} = \frac{1-y^2}{\left( 1+y^2 \right)^2}.
\]
-
Bass F, 1969. A new product growth model for consumer durables. Management Science, 15, 215–227.
-
Cabrera, N.V., Jafelice, R.S.M., Bertone, A.M., Montroll’s model applied to a population growth data set using type-1 and type-2 fuzzy parameters, Biomatematica, 2016, Vol. 26, pp. 145--160.
-
Gompertz B, 1825. On nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philosophical Transactions of the Royal Society of London, 115, 513–585.
-
Hutchinson, G.E., An introduction to population ecology, Yale University Press, New Haven, CT, 1978, 260p.
-
Janoschek A, 1957. Das reaktionskinetische Grundgesetz und seine Beziehungen zum Wachstums- und Ertragsgesetz. Statistische Vierteljahresschrift, 10, 25–37.
-
Kiviste, A.K., Mathematical functions of forest growth. Estonian Agricultural Academy, 1988, Tartu. 108 p + Supplement 171 p. (In Russian).
-
Korf, V., Contribution to the mathematical definition of forest stands growth.
(Příspěvek k matematické definici vzrůstového zákona hmot lesních porostů). Lesnická práce, 1939, Vol. 18, pp. 339--379 (In Czech).
-
Ludwig, D., Jones, D.D., and Holling, C.S., Journal of Animal Ecology, 1978, 47, Issue 1, 315--332.
-
Makeham, W.M., On the integral of Gompertz's function for expressing the values of sums depending upon the contingency of life, Journal of the Institute of Actuaries and Assurance Magazine, 1873, Vol. 17, No. 5, pp. 305--327.
-
Panik, M.J., Growth Curve Modeling: Theory and Applications, Wiley, 2014.
-
Richards, F.J., A flexible growth curve for empirical use. Journal of Experimental Botany, 1959, Vol. 10, No. 29, pp. 290--300.
-
Smith, D.A., Human population growth: Stability or Explosion?, Mathematics Magazine, 1977, Vol. 50, No. 4, pp. 186--197. https://www.jstor.org/stable/23686557
-
Thieme, H., Mathematics in Population Biology, Princeton: Princeton Univer-sity Press, 2003.
-
Tsoularis, A., Wallace, J., 2002. Analysis of logistic growth models. Mathematical Biosciences, 179(1), 21–55.
-
Verhulst, P.F., 1838. Notice sur la loi que la population suit dans son accroissement. Correspondence Mathematique et Physique, 10, 113–121.
-
von Bertalanffy, L, Problems of organic growth, Nature, 1949, , vol. 163, no.4135, pp. 156-158. doi:10.1038/163156a0
-
von Foerster, H., Mora, P.M., Amiot, L.W., Doomsday, Friday, 13 November, A.D. 2026, Science, 1960, , vol. 132, pp. 1291--1295.
-
Weibull, W., 1951. A statistical distribution function of wide applicability. Journal of Applied Mechanics, 18(3), 293–297.
-
Zeide, B., Analysis of growth equations, Forest Science, 1993, Vol. 39, No. 3, pp. 594--616.