Consider systems of linear differential equations with constant coefficients

\begin{equation} \label{EqPhase.1} \dot{\bf x} = {\bf A}\,{\bf x} , \qquad\mbox{where} \quad \dot{\bf x} = {\text d}{\bf x}/{\text d}t , \end{equation}

where A is a square matrix. When matrix A in Eq.\eqref{EqPhase.1} is a 2×2 matrix and x(t) is a 2-dimensional column vector, this case is called planar, and we can take advatange of this to visualize the situation.

Since we know the structure of solutions to Eq.\eqref{EqPhase.1} from its fundamental matrix \( e^{{\bf A}\,t} , \) it is expected that the analysis of solutions near the origin is the most fruitful. It is not a surprise that this case requires a special attention.

An autonomous vector differential equation

\begin{equation} \label{EqPhase.2} \dot{\bf x} = {\bf f} ({\bf x}) , \qquad\mbox{where} \quad \dot{\bf x} = {\text d}{\bf x}/{\text d}t , \end{equation}

is said to have an equilibrium solution (also called stationary or critical point) x(t) = p if f(p) = 0. The critical point is called isolated if there is a neighborhood of the stationary point not containing another critical point.

Recall that a neighborhood of a point p is any set in ℝⁿ that contains an open ball \( \| {\bf x} - {\bf p} \| = \sqrt{\left( x_1 - p_1 \right)^2 + \cdots +\left( x_n - p_n \right)^2 } < \varepsilon \) centered at p = [p₁, …, p_n]^T. An equilibrium (also called stationary) solution of the autonomous system \eqref{EqPhase.2} is a point where the derivative of \( {\bf x}(t) \) is zero. An equilibrium solution is a constant solution of the system, and is usually called a critical point. For a linear system \( \dot{\bf x} = {\bf A}\,{\bf x}, \) an equilibrium solution occurs at each solution of the system (of homogeneous algebraic equations) \( {\bf A}\,{\bf x} = {\bf 0} . \) As we have seen, such a system has exactly one solution, located at the origin, if \( \det{\bf A} \ne 0 .\) If \( \det{\bf A} = 0 , \) then there are infinitely many solutions, and the critical point is not isolated.

Previously, we used a direction (or tangent) field to depict the behavior of solutions without actual solving the differential equation. Now we are going to enhance its features by adding arrows to accommodate time presence and plot some typical solutions. The accurate tracing of the parametric curves of the solutions is not an easy task without computers. However, we can obtain a very reasonable approximation of a trajectory by using the very same idea behind the slope field, namely the tangent line approximation.

The phase portrait of Eq.\eqref{EqPhase.1} or in general, \eqref{EqPhase.2}, is a geometric representation of the trajectories of a dynamical system in the phase plane. The phase portrait contains some typical solution curves along with arrows indicating time variance of solutions (from corresponding direction field) and possible separatrices (if any).

Recall that a separatrix is the boundary separating two modes of behaviour in a differential equation and not every dynamoc system has a separatrix. A sketch of a particular solution in the phase plane is called the trajectory or orbit or streamline of the solution. Solutions of Eq.\eqref{EqPhase.1} are plotted as parametric curves (with t as the parameter) on the Cartesian plane tracing the path of each particular solution \( {\bf x} = \left[ x_1 (t) , x_2 (t) \right]^{\mathrm T} , \ -\infty < t < \infty . \) Similar to a direction field for a single differential equation, a phase portrait is a graphical tool to visualize how the solutions of a given system of differential equations would behave in a neighborhood of the critical point.

We introduce a subroutine (function) that will be used later for plotting phase portraits.


function [e,v] = plot_phase(A, xlimits, ylimits, step, plot_sepx, plot_sol, x0)
    %plot_phase([1 2; 2 4], [-1,1], [-1,1], 0.1, 1)
    % Setup plot limits
    x = xlimits(1):step:xlimits(2);
    y = ylimits(1):step:ylimits(2);
    lx = length(x);
    ly = length(y);
    % Setup grid of points to plot vectors on
    X = zeros(lx,ly);
    Y = zeros(lx,ly);
    for ii = 1:lx
        X(ii,:) = x;
    end
    X = reshape(X',[1,lx*ly]);
    for ii = 1:ly
        Y(ii,:) = y;
    end
    Y = reshape(Y,[1,lx*ly]);

    % Calculate Derivatives at every point
    U = zeros(1,lx*ly);
    V = zeros(1,lx*ly);
    for ii = 1:(lx*ly)
        der = A*[X(ii);Y(ii)];
        der=der/norm(der);
        U(ii) = der(1);
        V(ii) = der(2);
    end
    % Plot quiver
    figure
    hold on
    % Find Eigenvalues and Vectores
    e = eig(A);
    [v,~] = eig(A);
    % Optionally plot the seperatrix
    if plot_sepx
        if imag(e(1)) == 0
            % Node
            if e(1) == e(2)
                % Repeated Eigenvalues
                plot(5*[v(1), -v(1)], 5*[v(2), -v(2)],'LineWidth',2)
            else
                % Non-repeated eigenvalues, check for 0-value eigenvalues
                if e(2)
                    plot(5*[v(1,1), -v(1,1)], 5*[v(2,1), -v(2,1)], 'r','LineWidth',2)
                end
                if e(1)
                    plot(5*[v(1,2), -v(1,2)], 5*[v(2,2), -v(2,2)], 'r','LineWidth',2)
                end
            end
        end
    end
    % Optionally plot some solution curves
    if plot_sol
        odefun = @(t,x) A*x;
        [~,C] = size(x0);
        t0 = 0;
        tf = 20;
        for c = 1:C
            [t,y] = ode45(odefun, [t0, tf], x0(:,c));
            plot(y(:,1), y(:,2), 'g', 'Linewidth', 2)
            plot(y(1,1), y(1,2), 'go', 'MarkerSize', 10);
            plot(y(end,1), y(end,2), 'gs', 'MarkerSize', 10);
        end
    end
    % Plot Phase Portrait
    quiver(X,Y,U,V,0.5);
    % Plot Origin
    plot(0,0,'*k', 'MarkerSize', 10)
    % Set Plot Window dimensions
    xlim([ylimits(1),xlimits(2)]);
    ylim([ylimits(1),ylimits(2)]);
end

We will classify the critical points of various systems of first order linear differential equations by their stability. Since the general treatment of stability and instability is given in Part III of this tutorial, it is reasonable to provide its descriptive definition.

A critical point is called an attractor or sink if every solution in a proximity of it moves toward to the stationary point (so it converges to the critical point) as t → +∞. Alternatively, if trajectories near a stationary point leave it as t → +∞, then the critical point is referred to as the repeller or source.

Remember that solutions to constant coefficient linear system of differential equations exist for all t ∈ (−∞, ∞). Since the independent variable t is associated with time (which in reality is not invertible), we are mostly interested in understanding the behavior of solutions when t → +∞. However, an attractor becomes a repeller when you consider t → −∞ and vice versa. Each set of initial conditions is represented by a different curve, or point. They consist of a plot of typical trajectories in the state space. This reveals information such as whether a critical point is an attractor, or a repeller or limit cycle is present for the chosen parameter value.

In addition, due to the truly two-dimensional nature of the parametric curves, we will also classify the type of those critical points based on the behavior of solutions near equilibria (or, rather, by the shape formed by the trajectories about each critical point).

In our study of phase portraits and critical points, we will encounter four types of critical points: nodes, saddle point, spiral, and center. Note that this is typical only for two-dimensional problems. Additionally, these critical points are based on the eigenvalues and eigenvectors of the constant coefficient linear system of differential equations. The table below emphasizes the relationship between the stability and type of critical point based on the eigenvalues.

Singular Matrices

If a square matrix is singular, then at least one of its eigenvalues is zero. In this case, the origin is not an isolated critical point and there is a line of stationary points. This line is an eigenspace corresponding to the zero eigenvalue and it is also a separatrix in the phase portrait.

Example 1: Consider the 2×2 matrix

\[ {\bf A} = \begin{bmatrix} 1&2 \\ 2& 4 \end{bmatrix} . \]

It has two real eigenvalues, one of each is zero

Then we find the corresponding eigenvectors:

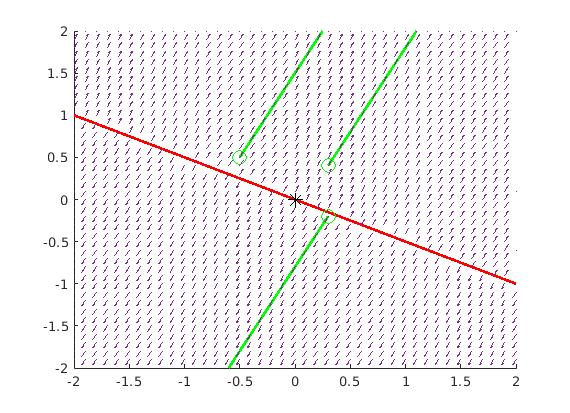
So we know that the eigenvalue λ = 0 has a corresponding eigenvector [−2, 1] (matlab provides its normalized value dividing by 5^½). Then we plot the direction field along with the separatrix corresponding to the eigenspace of λ = 0. Separatrix is an example of non-isolated equilibria.


close all
xlims = [-2,2];
ylims = [-2,2];
step = 0.1;
x0 = [-0.5, 0.5; 0.3, 0.4; .3, -.2]';
A1 = [1 2; 2 4];
[e1,v1] = plot_phase(A1, xlims,ylims, step, 1, 1, x0);

■

Isolated Equilibria

As a rule, we will only consider systems of linear differential equations whose coefficient matrix A has a nonzero determinant.

In two-dimensional space, it is possible to completely classify the critical points of various systems of first order linear differential equations by their stability. In addition, due to the truly two-dimensional nature of the parametric curves, we will also classify the type of those critical points by their shapes (or, rather, by the shape formed by the trajectories about each critical point). Their classification is based on eigenvalues of the coefficient matrix. Therefore, we consider different cases.

There are four types of critical points. To characterize them, it is convenient to use polar coordinates. Suppose that the solution curve of the autonomous planar differential equation dx/dt = f(x) can be written as x = x(t), y = y(t), where x = [x(t), y(t)]^T is a two-dimensional column vector. Then in polar coordinates, their trajectory can be written as

\begin{equation} \label{EqPhase.3} r = \rho (t) \ge 0, \qquad \theta = \omega (t) , \end{equation}

with x(t) = ρ(t) cosω(t), y(t) = ρ(t) sinω(t). For matrix \( {\bf A} = \begin{bmatrix} a & b \\ c& d \end{bmatrix} , \) the polar variables satisfy the equations:

\begin{equation} \label{EqPhase.4} \dot{r} = r \left[ a\,\cos^2 \theta + \left( b+c \right) \cos\theta\,\sin\theta + d\,\sin^2 \theta \right] , \qquad \dot{\theta} = c\,\cos^2 \theta + \left( d-a \right) \cos\theta\,\sin \theta -b\,\sin^2 \theta . \end{equation}

Nodes

A critical point (0,0) of the constant coefficient autonomous equation \eqref{EqPhase.1} is said to be a node if \( \lim_{t\to +\infty} \left\vert \omega (t) \right\vert = \) constant or \( \lim_{t\to -\infty} \left\vert \omega (t) \right\vert = \) constant, when x(t) belongs to some neighborhood of the critical point. In the former case, the critical point is called nodal sink, and in latter, it is a nodal source.

Nodes are critical points with the property that a trajectories arrive or depart from the critical point along some directory. In turn, there are known of three types of nodes:

proper node or star when every semi-line from the critical point is a tangent to some orbit;
improper node when there are at most two directions along which trajectories approach the critical point;
degenerate node when there is only one direction along which orbits approach the critical point.

An equilibrium solution of an autonomous system of differential equations \( \dot{\bf x} = {\bf f}\left( {\bf x}\right) \) is called a node if nearby trajectories approach it or depart from the critical point along some definite direction (semi-straight line). Correspondingly, the critical point is referred to as nodal sink or nodal source, depending whether trajectories approach the stationary point or depart from it as t → +∞.

The trajectories that are the eigenvectors move in straight lines. The rest of the trajectories move, initially when near the critical point, roughly in the same direction as the eigenvector of the eigenvalue with the smaller absolute value. Then, farther away, they would bend toward the direction of the eigenvector of the eigenvalue with the larger absolute value.

For constant coefficient linear differential equations, classification of critical points can be performed based on eigenvalues of the corresponding constant matrix.

Case 1: Diagonal real-valued matrix with the same entries and of the same sign. A proper node can be observed only when the matrix of the system is a constant real multiple of the diagonal matrix:

\[ \alpha \, \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} = \begin{bmatrix} \alpha &0 \\ 0&\alpha \end{bmatrix} \quad \mbox{ where } \alpha \quad \mbox{is an arbitrary nonzero constant} . \]

In this case, the system is uncoupled and each equation can be solved separately. Numbers on the diagonal are eigenvalues of the matrix. See the following example. Then the general solution is

\[ {\bf y}(t) = \begin{bmatrix} y_1 (t) \\ y_2 (t) \end{bmatrix} = c_1 \begin{bmatrix} \xi \\ 0 \end{bmatrix} e^{\lambda\,t} + c_2 \begin{bmatrix} 0 \\ \eta \end{bmatrix} e^{\lambda\,t} , \]

with arbitrary constants c₁ and c₂.

Example 2: Consider the following 2×2 matrices

\[ {\bf A}_1 = \begin{bmatrix} 1&0 \\ 0& 1 \end{bmatrix} , \qquad {\bf A}_2 = \begin{bmatrix} -1&\phantom{-}0 \\ \phantom{-}0& -1 \end{bmatrix} . \]

Upon plotting the corresponding phase portraits, we see that matrix A₁ generate proper nodal source at the origin, whereas matrix A₂ corresponds to proper nodal sink.


close all
xlims = [-2,2];
ylims = [-2,2];
step = 0.1;
x0 = [-0.5, 0.5; 0.3, 0.4; .3, -.2]';
A2a = [1 0; 0 1];
A2b = [-1 0; 0 -1];
[e2a,v2a] = plot_phase(A2a, xlims,ylims, step, 0, 1, x0);
[e2b,v2b] = plot_phase(A2b, xlims,ylims, step, 0, 1, x0);


Figure 2: Proper nodal source, matrix A₁.		Figure 3: Proper nodal sink, matrix A₂.


N = chebop(@(t,u,v) [diff(u)-u; diff(v)-v], [0 10]);
quiver(N, [0 5 0 5],'xpts',30,'ypts',30,'normalize',true,'scale',.4)
hold on
for rabbits = -1:.2:1
    N.lbc = @(u,v) [u - rabbits; v - 1]; % Initial conditions
    [u, v] = N\0;
    arrowplot(u, v)
end
hold off
title('Proper node')
xlabel('x'), ylabel('y')

■

Case 2: Distinct real eigenvalues of the same sign. Then the general solution of the linear system \( \dot{\bf x} = {\bf A}\,{\bf x}, \) is

\[ {\bf x} (t) = c_1 \,{\bf \xi} \, e^{\lambda_1 t} + c_2 \,{\bf \eta} \, e^{\lambda_2 t} , \]

where \( \lambda_1 \) and \( \lambda_2 \) are distinct real eigenvalues, \( {\bf \xi} \) and \( {\bf \eta} \) are corresponding eigenvectors, and \( c_1 , c_2 \) are arbitrary real constants.

When eigenvalues λ₁ and λ₂ are both positive, or are both negative, the phase portrait shows trajectories either moving away from the critical point toways infinity (for positive eigenvalues), or moving directly towards and converging to the critical point (for negative eigenvalues). The trajectories that are the eigenvectors move in straight lines. The rest of the trajectories move, initially when near the critical point, roughly in the same direction as the eigenvector of the eigenvalue with the smaller absolute value. Then, farther away, they would bend toward the direction of the eigenvector of the eigenvalue with the larger absolute value. This type of critical point is called a node. It is asymptotically stable if eigenvalues are both negative, unstable if eigenvalues are both positive.

Stability: It is unstable if both eigenvalues are positive; asymptotically stable if they are both negative.

Example 3: We start with the diagonal matrix and corresponding autonomous differential equation

\[ {\bf B} = \begin{bmatrix} 1&0 \\ 0&2 \end{bmatrix} , \qquad \frac{{\text d}{\bf y}}{{\text d}t} = {\bf B} \,{\bf y}(t) . \]

So the given system is decoupled

\[ \dot{x} = x , \qquad \dot{y} = 2\,y , \]

with the general solution

\[ {\bf y}(t) = \begin{bmatrix} x(t) \\ y(t) \end{bmatrix} = c_1 \begin{bmatrix} 1 \\ 0 \end{bmatrix} e^{t} + c_2 \begin{bmatrix} 0 \\ 1 \end{bmatrix} e^{2t} . \]

Here, c₁ and c₂ are arbitrary constants. We can find the explicit solution from the equation

\[ \frac{{\text d}y}{{\text d}x} = \frac{\dot{y}}{\dot{x}} = \frac{2y}{x} \qquad \Longrightarrow \qquad y = x^2 . \]

Octave version:

We plot the direction field along with some trajectories and separatrix y = 0 (in red). Another eigenspace x = 0 (vertical line) is not actually a separatrix, and it is not shown. The origin is a nodal source---repeller.


close all
xlims = [-2,2];
ylims = [-2,2];
step = 0.1;
x0 = [-0.5, 0.5; 0.3, 0.4; .3, -.2]';
A3a = [1 0; 0 2];
A3b = [-1 0; 0 -3];
[e3a,v3a] = plot_phase(A3a, xlims,ylims, step, 1, 1, x0);
[e3b,v3b] = plot_phase(A3b, xlims,ylims, step, 1, 1, x0);

For another diagonal matrix

\[ {\bf B}_2 = \begin{bmatrix} -1&\phantom{-}0 \\ \phantom{-}0&-3 \end{bmatrix} , \qquad \frac{{\text d}{\bf y}}{{\text d}t} = {\bf B}_2 \,{\bf y}(t) . \]

we have a similar phase portrait, but the origin becomes nodal sink.

Octave version:

Upon separation of variables, we obtain its general solution

\[ \frac{{\text d}y}{{\text d}x} = \frac{\dot{y}}{\dot{x}} = \frac{-3y}{-x} \qquad \Longrightarrow \qquad y = x^3 . \]

We plot the direction field along with some trajectories and separatrix y = 0 (in red). The origin is a nodal sink (attractor).


close all
xlims = [-2,2];
ylims = [-2,2];
step = 0.1;
x0 = [-0.5, 0.5; 0.3, 0.4; .3, -.2]';
A3a = [1 0; 0 2];
A3b = [-1 0; 0 -3];
A3c = [-5 2; -4 1];
A3d = [2 1; 1 2];
[e3a,v3a] = plot_phase(A3a, xlims,ylims, step, 1, 1, x0);
[e3b,v3b] = plot_phase(A3b, xlims,ylims, step, 1, 1, x0);
[e3c,v3c] = plot_phase(A3c, xlims,ylims, step, 1, 1, x0);
[e3d,v3d] = plot_phase(A3d, xlims,ylims, step, 1, 1, x0);

■

Example 4: Consider two matrices

\[ {\bf A}_1 = \begin{bmatrix} -5&2 \\ -4&1 \end{bmatrix} , \qquad {\bf A}_2 = \begin{bmatrix} 2&1 \\ 1&2 \end{bmatrix} \]

A1 = {{-5, 2}, {-4, 1}}
Eigenvalues[A1]

{-3, -1}

This tells us that the origin is the attractor because both eigenvalues are real negative numbers.

Eigenvectors[A1]

{{1, 1}, {1, 2}}

So we know that separatrix is going along each eigenvector corresponding to distinct eigenvalues. We plot the corresponding eigenlines; one of them corresponding to the largest absolute value (λ = −3) is indicated by double arrow and another eigenline (λ = −1) is labeled by a single arrow.

arr1 = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{1, 1}, {0, 0}}]}];
arr1a = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{1, 1}, {0.1, 0.1}}]}];
arr2 = Graphics[{Purple, Thick, Arrowheads[0.06], Arrow[0.5*{{1, 2}, {0.2, 0.4}}]}];
arr4 = Graphics[{Purple, Thick, Arrowheads[0.06], Arrow[0.5*{{-1, -2}, {-0.2, -0.4}}]}];
arr3 = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{-1, -1}, {0, 0}}]}];
arr3a = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{-1, -1}, {-0.1, -0.1}}]}];
sp = StreamPlot[{-5*x + 2*y, -4*x + y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific", StreamStyle -> Blue];
Show[arr1, arr1a, arr2, arr3, arr3a, arr4, sp]

Now we perform a similar job with another matrix A₂.

A2 = {{2, 1}, {1, 2}}
Eigenvalues[A2]

{3, 1}

This tells us that the origin is a repeller because both eigenvalues are real positive numbers.

Eigenvectors[A2]

{{1, 1}, {-1, 1}}

vp = VectorPlot[{2*x + y, x + 2*y}, {x, -1, 1}, {y, -1, 1}, StreamStyle -> Blue];
arr1 = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {1, 1}}]}];
arr1a = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {0.9, 0.9}}]}];
arr2 = Graphics[{Orange, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {-1, 1}}]}];
arr4 = Graphics[{Orange, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {1, -1}}]}];
arr3 = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {-1, -1}}]}];
arr3a = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {-0.9, -0.9}}]}];
Show[arr1, arr1a, arr2, arr3, arr3a, arr4, vp]

The graphs below show phase portrait around the critical point (origin) along with separatricies that go along eigenlines (generated by eigenvectors). The eigenline corresponding to the dominant eigenvalue (having largest absolute value) is shown with double arrow and red color.


Figure 6: Improper nodal source with dominated separatrix labeled by double arrow.		Figure 7: Improper nodal sink.

■

Case 3: Repeated real eigenvalue with one eigenvector. If a square 2×2 matrix is not diagonal and has a defective (repeated) eigenvalue, then the matrix has only one eigenvector. It is not diagonalizable and its general solution is of the form

\[ {\bf x} (t) = e^{{\bf A}t} {\bf c} = c_1 \,{\bf \xi} \, e^{\lambda\, t} + c_2 \,e^{\lambda\, t} \left( t\,{\bf \xi} + {\bf \eta} \right) , \]

where ξ is the eigenvector and η is so called the generalized eigenvector. The original is the degenerate node, either attractor if its eigenvalue is negative, or repeller if its eigenvalue is positive. The trajectories either all diverge away from the critical point towards infinity (when eigenvalue λ > 0) or all converge towards the critical point (when eigenvalue λ < 0). This type of critical point is called an improper node. It is asymptotically stable if \( \lambda <0 ,\) unstable if \( \lambda >0 .\) The phase portrait is presented in the following example.

Example 5: Consider two matrices

\[ {\bf A}_3 = \begin{bmatrix} 5&-3 \\ 3& -1 \end{bmatrix} , \qquad {\bf A}_4 = \begin{bmatrix} -5&-3 \\ \phantom{-}3&\phantom{-}1 \end{bmatrix} . \]

Using matlab, we determine that matrix A₃ has one defective eigenvalue λ = 2; this tells us that the origin is the repeller.

A3 = {{5, -3}, {3, -1}};
Eigenvalues[A3]

{2, 2}

Eigenvalues[A3]

{{1, 1}, {0, 0}}

We plot the direction field and the separatrix (in red) that is spanned on the eigenvectors.

vp = VectorPlot[{5*x - 3*y, 3*x - y}, {x, -1, 1}, {y, -1, 1}, StreamStyle -> Blue];
line = Graphics[{Red, Thick, Line[{{-1, -1}, {1, 1}}]}];
Show[line, vp]

Then we repeat the same job for matrix A₄.

A4 = {{-5, -3}, {3, 1}};
Eigenvalues[A3]

{-2, -2}

Eigenvalues[A4]

{{-1, 1}, {0, 0}}

sp = StreamPlot[{-5*x - 3*y, 3*x + y}, {x, -1, 1}, {y, -1, 1}, StreamStyle -> Blue];
line = Graphics[{Red, Thickness[0.01], Line[{{-1, 1}, {1, -1}}]}];
Show[line, sp]


Figure 8: Degenerate nodal source.		Figure 9: Degenerate nodal sink.

■

Saddle points

A critical point (0,0) of the constant coefficient autonomous equation \eqref{EqPhase.1} is said to be a saddle point if there are two trajectories approaching the origin along opposite directions, and all other orbits close to either of them and to (0,0) tend away from them as t becomes infinite.

Case 4: Distinct real eigenvalues are of opposite signs. In this type of phase portrait, the trajectories given by the eigenvectors of the negative eigenvalue initially start at infinity before moving towards and eventually converging at the critical point. The trajectories that represent the eigenvectors of the positive eigenvalue move in exactly the opposite way: starting at the critical point before diverging to infinity. Every other trajectory starts at infinity, moves toward but never converges to the critical point, and then changes direction and moves back towards infinity. All the while it would roughly follow the 2 sets of eigenvectors. This type of critical point is called a saddle point. It is always unstable.

Stability: It is always unstable.

Example 6: Consider a system of ordinary differential equations

\[ \frac{{\text d}}{{\text d} t} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1&2 \\ 2&1 \end{bmatrix} \, \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} . \]

We can enter this equation into Mathematica either as a vector

f[x_, y_] = {x + 2*y, 2*x + y}; Print["X' = ", MatrixForm[f[x, y]]]

\( X' = \begin{pmatrix} x+2\,y\\ 2\,x +y \end{pmatrix} \)

or as two equations

Print["x' = ", f[x, y][[1]], ", y' = ", f[x, y][[2]]]

\( x' = x + 2\,y, \quad y' = 2\,x + y \)

The coefficient matrix \( {\bf A} = \begin{bmatrix} 1&2 \\ 2&1 \end{bmatrix} \) has two distinct real eigenvalues \( \lambda_1 =3 \) and \( \lambda_2 =-1 . \) Therefore, the critical point, which is the origin, is a saddle point, unstable. We plot the corresponding phase portrait using the following codes. Mathematica provides us at least two options: either StreamPlot or VectorPlot (for the latter we give two versions without normalization and with it).

splot = StreamPlot[{x + 2*y, 2*x + y}, {x, -4, 4}, {y, -3, 3}, StreamColorFunction -> "Rainbow"];
Manipulate[ Show[splot, ParametricPlot[ Evaluate[ First[{x[t], y[t]} /.
NDSolve[{x'[t] == x[t] + 2*y[t], y'[t] == 2*x[t] + y[t], Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0, T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}}, Locator}, SaveDefinitions -> True]

and the phase portrait with VectorPlot

Show[VectorPlot[f[x, y], {x, -4, 4}, {y, -4, 4}], Frame -> True, BaseStyle -> {FontFamily -> "Times", FontSize -> 14}]

Show[VectorPlot[f[x, y]/Norm[f[x, y]], {x, -4, 4}, {y, -4, 4}], Frame -> True, BaseStyle -> {FontFamily -> "Times", FontSize -> 14}]

StreamPlot	VectorPlot	VectorPlot with normalization

It is clear that the origin is an unstable equilibrium solution. ■

Spiral points

A critical point (0,0) of the constant coefficient autonomous equation \eqref{EqPhase.1} is said to be a spiral point if the following three conditions hold for all orbits in some neighbohood of the origin.

all trajectories are defined on t₀ < t < ∞ or −∞ < t < t₀ for some t₀;
\( \lim_{t\to +\infty} r (t) = 0 \) or \( \lim_{t\to -\infty} r (t) = 0 . \)
\( \lim_{t\to +\infty} \left\vert \omega (t) \right\vert = \infty \) or \( \lim_{t\to -\infty} \left\vert \omega (t) \right\vert = \infty . \)

Case 5: Complex conjugate eigenvalues. When the real part of eigenvalues is nonzero, the trajectories still retain the elliptical traces. However, with each revolution, their distances from the critical point grow/decay exponentially according to the term \( e^{\Re\lambda\,t} , \) where \( \Re\lambda \) is the real part of the complex λ, the eigenvalue. Therefore, the phase portrait shows trajectories that spiral away from the critical point toways infinity (when \( \Re\lambda > 0 \) ), or trajectories that spiral toward, and converge to the critical point (when \( \Re\lambda < 0 \) ). This type of critical point is called a spiral point. It is asymptotically stable if \( \Re\lambda < 0 ,\) it is unstable if \( \Re\lambda > 0 . \)

Example 7: Consider two matrices

\[ {\bf A}_5 = \begin{bmatrix} -1&13 \\ -1& \phantom{1}3 \end{bmatrix} , \qquad {\bf A}_6 = \begin{bmatrix} -3&13 \\ -1&\phantom{3}1 \end{bmatrix} . \]

The eigenvalues of both matrices are complex conjugate numbers:

A5 = {{-1, 13}, {-1, 3}}; Eigenvalues[A5]

{1 + 3 I, 1 - 3 I}

and

A6 = {{-3, 13}, {-1, 1}}; Eigenvalues[A6]

{-1 + 3 I, -1 - 3 I}

		We plot the direction field in a neighborhood of the asymptotically stable stationary point. Note that trajectories approach the origin in clockwise direction. StreamPlot[{-3x + 13y, -x + y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
Spiral critical point for matrix A₆.		Mathematica code

		We plot the direction field in a neighborhood of the asymptotically stable stationary point for matrix −A₆. Note that trajectories approach the origin in counterclockwise direction. StreamPlot[{3x - 13y, x - y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Detailed", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
Spiral asymptotically stable critical point for matrix −A₆.		Mathematica code

Now we do a similar job for matrix A₅ that has unstable critical point at the origin.

		We plot the direction field in a neighborhood of the ustable stationary point. Note that trajectories depart from the origin in clockwise direction. StreamPlot[{-x + 13y, -x + 3y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Minimal", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
Spiral unstable critical point for matrix A₅.		Mathematica code

		We plot the direction field in a neighborhood of the unstable stationary point for matrix −A₅. Note that trajectories depart from the origin in counterclockwise direction. StreamPlot[{x - 13y, x - 3y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Web", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
Spiral unstable critical point for matrix −A₅.		Mathematica code

■

Center

A critical point (0,0) of the constant coefficient autonomous equation \eqref{EqPhase.1} is said to be a center if there exists a neighborhood containing countably many closed trajectories, each containing the origin and diameters tend to zero.

Case 6: Two pure complex conjugate eigenvalues. When the real part of the eigenvalues is zero, the trajectories neither converge to the critical point nor move toways infinitey. Rather, they stay in constant, elliptical (or, rarely, circular) orbits. This type of critical point is called a center. It has a unique stability classification shared by no other: stable (or neutrally stable).

Example 8: Consider the system of differential equations

\[ \frac{{\text d}{\bf x}}{{\text d}t} \equiv \frac{\text d}{{\text d}t} \begin{bmatrix} x(t) \\ y(t) \end{bmatrix} = \begin{bmatrix} x-y \\ 5x-y \end{bmatrix} . \]

The corresponding matrix

\[ {\bf A} = \begin{bmatrix} 1&-1 \\ 5&-1 \end{bmatrix} \]

has two complex conjugate pure imaginary eigenvalues

B = {{1, -1}, {5, -1}}; Eigenvalues[B]

{2 I, -2 I}

		We plot the direction field. StreamPlot[{x -y, 5*x - y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
Center critical point.		Mathematica code

■


figure(1)
plot(x, y, 'Color', [1 0 0]) %blue line
hold on
plot(x, z, 'Color', [0 1 0]) %green line

Eigenvalues	Type of Critical Point	Stability
λ₁ > λ₂ > 0	Nodal source (node)	Unstable
λ₁ < λ₂ < 0	Nodal sink (node)	Asymptotically stable
λ₁ < 0 < λ₂	Saddle point	Unstable
λ₁ = λ₂ > 0 diagonal matrix	Proper node (star)	Unstable
λ₁ = λ₂ < 0 diagonal matrix	Proper node (star)	Asymptotically stable
λ₁ = λ₂ > 0 missing eigenvector	Improper/degenerate node	Unstable
λ₁ = λ₂ < 0 missing eigenvalue	Improper/degenerate node	Asymptotically stable
λ = α ± jβ, α > 0	Spiral point	Unstable
λ = α ± jβ, α < 0	Spiral point	Asymptotically stable
λ = ± jβ	Center	Stable

matlab plots phase portraits