We consider the Duffing oscillator under periodic driven force:
\begin{equation} \label{EqFD.1}
\ddot{x} + x + \varepsilon \,x^3 = F\,\cos \omega t,
\end{equation}
and
\begin{equation} \label{EqFD.2}
\ddot{x} + x + \varepsilon \,x^3 = F\,\sin \omega t.
\end{equation}
Here ε is a small parameter and
F is the amplitude of oscillating force. We consider both equations, \eqref{EqFD.1} and \eqref{EqFD.2} under homogeneous conditions
\[
x(0) = 0 , \qquad \dot{x}(0) = 0.
\]
Using the spring analogy
for this differential equation, for a fixed value of ω and small value of amplitude
F,
the spring oscillates quite nicely; as
F is increased the oscillations increase in
amplitude until the threshold is reached and the spring breaks (the solution becomes unbounded).

|
|

|
|
For the initial value problem
\[
\ddot{x} + x - \frac{1}{6} \,x^3 = F\,\cos \omega t, \qquad x(0) = 0, \quad \dot{x}(0) =0 ,
\]
we try to determine the boundary on (F, ω)-plane where solutions of the Duffing equation above are bounded.
clear all
clc
epsilon = -1/6;
tmax = 150;
oms = 30;
warning('off','all')
opts = odeset('Reltol',1e-13,'AbsTol',1e-14);
t_span = [0, tmax];
init = [0, 0];
omega = 0.1;
tmaxi = tmax;
stability = zeros(oms,2);
for i = 1:oms
F = 0;
tmax = tmaxi;
disp(omega)
while tmax > tmaxi - 2
F = F + 0.5;
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
tmax = max(t);
end
while tmax < tmaxi - 2
F = F - 0.1;
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
tmax = max(t);
end
stability(i,:) = [omega, F];
omega = omega + 0.1;
end
figure
sz = 25;
c = linspace(1,10,oms);
scatter(stability(:,1),stability(:,2),sz,c,'filled')
ylabel('F')
xlabel('omega')
title('Stability boundary for initial x_0 = 0, dxdt_0 = 0')
init = [0, 1];
omega = 0.1;
stability = zeros(oms,2);
for i = 1:oms
F = 0;
tmax = tmaxi;
disp(omega)
while tmax > tmaxi - 2
F = F + 0.5;
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
tmax = max(t);
end
while tmax < tmaxi - 2
F = F - 0.1;
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
tmax = max(t);
end
stability(i,:) = [omega, F];
omega = omega + 0.1;
end
figure
scatter(stability(:,1),stability(:,2),sz,c,'filled')
ylabel('F')
xlabel('omega')
title('Stability boundary for initial x_0 = 0, dxdt_0 = 1')
function dwdt = duff(t,w,epsilon,F,omega)
x = w(1);
y = w(2);
dxdt = y;
dydt = - x - epsilon * x^3 + F * cos(omega*t);
dwdt = [dxdt;dydt];
end
|
|
The boundary of the domain where solutions of the Duffing equations subject to the homogeneous initial conditions are bounded.
|
|
The boundary of the domain where solutions of the Duffing equations subject to the initial conditions x(0) = 0, x'(0) = 1, are bounded.
|
|
matlab code.
|
There are at least two significant features observable on this stability boundary
curve. The first is the rather sharp dip in the curve forming a local and global
minimum. For this initial value problem, the global and local minimum occurs for ω ≈ 0.8852, discovered by Davis.
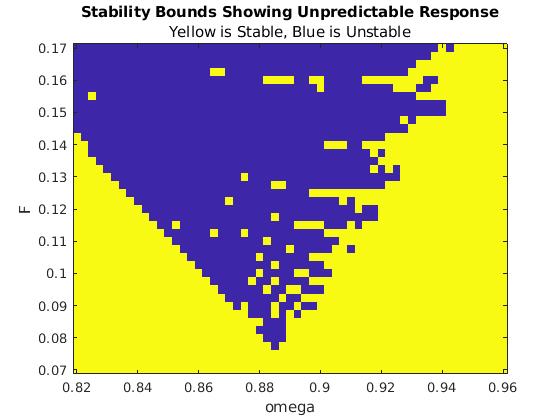
|
|
To make the boundary more clear, we write the code that produces an output with two colors---blue where values of (F, ω) cause unbounded solutions, and yellow when these values lead to bounded solutions.
clear all
clc
% runtime is about 10 sec for low precision
% prints out the omega values it solving for so you can check if the code
% is stuck somewhere
tic;
epsilon = -1/6;
tmax = 150;
% low precision -- misses a lot of detail, for quick testing
% runtime: 10 sec
oms = 0.820:0.0025:0.960;
fs = 0.070:0.0025:0.170;
warning('off','all')
opts = odeset('Reltol',1e-13,'AbsTol',1e-14);
t_span = [0, tmax];
init = [0, 0];
stability = zeros(length(fs),length(oms));
frow = 1:length(fs);
for i = 1:length(oms)
disp(oms(i))
temp = zeros(length(fs),1);
for f = frow
F = fs(f);
omega = oms(i);
warning('off','all')
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
if max(t) > tmax-2
temp(f) = 1;
end
end
stability(:,i) = temp;
end
figure
s = imagesc([oms(1) oms(length(oms))],[fs(1) fs(length(fs))],stability);
ax = gca;
ax.YDir = 'normal';
title("Stability Bounds Showing Unpredictable Response")
subtitle("Yellow is Stable, Blue is Unstable")
xlabel("omega")
ylabel("F")
hold off
toc;
function dwdt = duff(t,w,epsilon,F,omega)
x = w(1);
y = w(2);
dxdt = y;
dydt = - x - epsilon * x^3 + F * cos(omega*t);
dwdt = [dxdt;dydt];
end
|
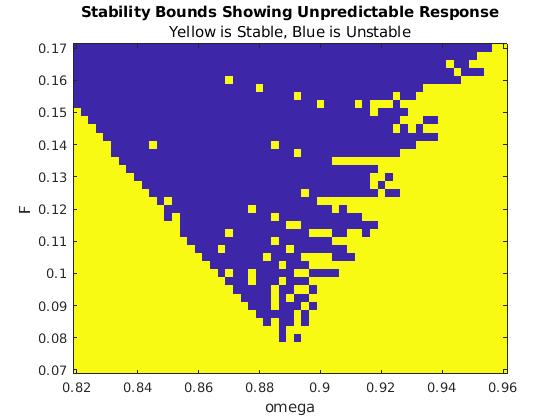
|
|
We repeat the same calculation when the forcing functions is sine, as in Eq.\eqref{EqFD.2}
clear all
clc
% runtime is about 10 sec for low precision
% prints out the omega values it solving for so you can check if the code
% is stuck somewhere
tic;
epsilon = -1/6;
tmax = 150;
% low precision -- misses a lot of detail, for quick testing
% runtime: 10 sec
oms = 0.820:0.0025:0.960;
fs = 0.070:0.0025:0.170;
warning('off','all')
opts = odeset('Reltol',1e-13,'AbsTol',1e-14);
t_span = [0, tmax];
init = [0, 0];
stability = zeros(length(fs),length(oms));
frow = 1:length(fs);
for i = 1:length(oms)
disp(oms(i))
temp = zeros(length(fs),1);
for f = frow
F = fs(f);
omega = oms(i);
warning('off','all')
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
if max(t) > tmax-2
temp(f) = 1;
end
end
stability(:,i) = temp;
end
figure
s = imagesc([oms(1) oms(length(oms))],[fs(1) fs(length(fs))],stability);
ax = gca;
ax.YDir = 'normal';
title("Stability Bounds Showing Unpredictable Response")
subtitle("Yellow is Stable, Blue is Unstable")
xlabel("omega")
ylabel("F")
hold off
toc;
function dwdt = duff(t,w,epsilon,F,omega)
x = w(1);
y = w(2);
dxdt = y;
dydt = - x - epsilon * x^3 + F * sin(omega*t);
dwdt = [dxdt;dydt];
end
|
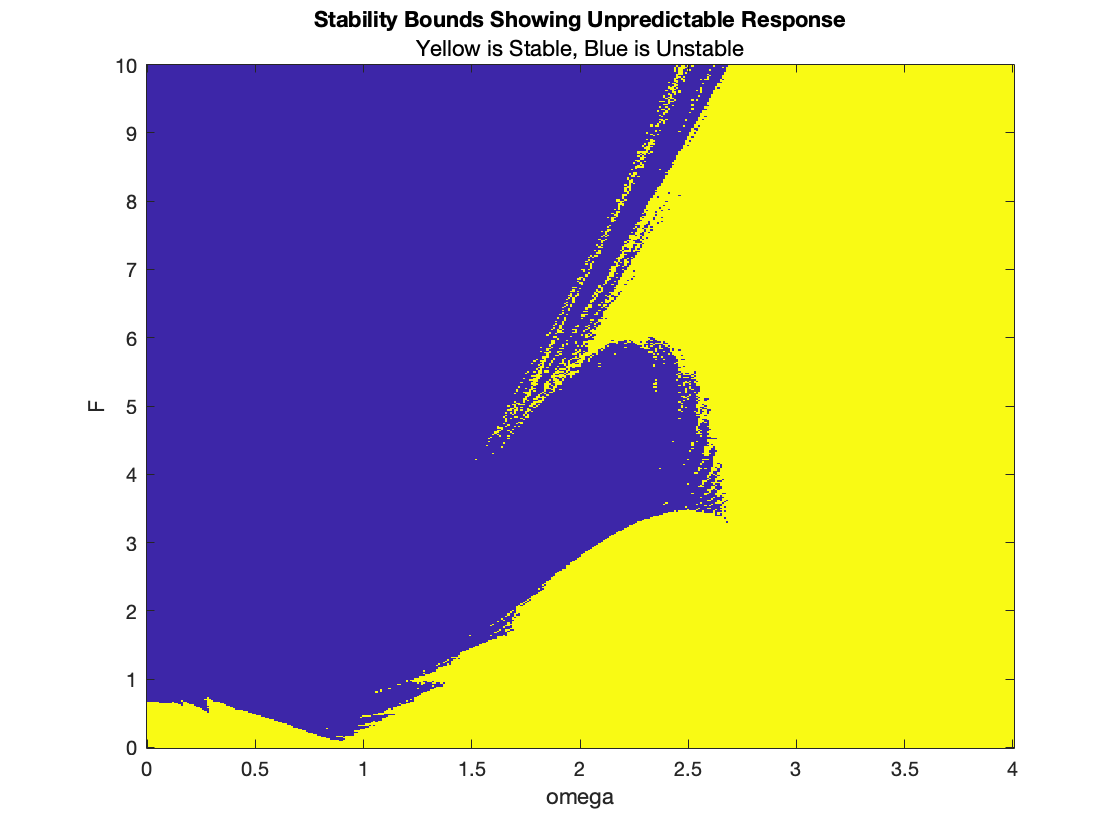
The resulting stability boundary obtained initially resembles the one obtained by
Davis as things go along quite nicely until ω reaches 2.6 where a sudden and
unexpected jump in the boundary occurs. Clearly this appears to be similar to a jump
discontinuity in the stability boundary curve.
This jump occurs between ω = 2.66 and F = 3.360 and ω = 2.67 and F = 9.901.
For values of ω larger than 2.67, the corresponding F values on the boundary curve
grow large; for example for ω = 3.1, the corresponding boundary F-value is 14.893.
For reasons of scale, we did not calculate boundary values for ω larger than 3.1.
We call the value ω = 2.67 the jump frequency although the term high resonance
frequency might be appropriate. In the spring analogy, this means that for ω just less
than the jump frequency it takes only a moderate amplitude (force) to brake the
spring, but for ω larger than the jump frequency it takes significantly more amplitude
to reach the breaking point.

|
|
First, we try to determine the boundary on (F, ω)-plane where solutions of the Duffing equation \eqref{EqFD.2} are bounded.
|

|
|
Next, we repeat our calculations for boundary determination with sine function, Eq.\eqref{EqFD.2}
|
As you see, these codes provide only rough estimation of the boundary. Therefore, we improve the code and run it on supercomputer.
clear all
clc
epsilon = -1/6;
tmax = 150;
oms = 30;
warning('off','all')
opts = odeset('Reltol',1e-13,'AbsTol',1e-14);
t_span = [0, tmax];
init = [0, 0];
omega = 0.1;
tmaxi = tmax;
stability = zeros(oms,2);
for i = 1:oms
F = 0;
tmax = tmaxi;
disp(omega)
while tmax > tmaxi - 2
F = F + 0.5;
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
tmax = max(t);
end
while tmax < tmaxi - 2
F = F - 0.1;
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
tmax = max(t);
end
stability(i,:) = [omega, F];
omega = omega + 0.1;
end
figure
sz = 25;
c = linspace(1,10,oms);
scatter(stability(:,1),stability(:,2),sz,c,'filled')
ylabel('F')
xlabel('omega')
title('Stability boundary for initial x_0 = 0, dxdt_0 = 0')
init = [0, 1];
omega = 0.1;
stability = zeros(oms,2);
for i = 1:oms
F = 0;
tmax = tmaxi;
disp(omega)
while tmax > tmaxi - 2
F = F + 0.5;
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
tmax = max(t);
end
while tmax < tmaxi - 2
F = F - 0.1;
[t, x] = ode113(@(t,w) duff(t,w,epsilon,F,omega), t_span, init, opts);
tmax = max(t);
end
stability(i,:) = [omega, F];
omega = omega + 0.1;
end
figure
scatter(stability(:,1),stability(:,2),sz,c,'filled')
ylabel('F')
xlabel('omega')
title('Stability boundary for initial x_0 = 0, dxdt_0 = 1')
function dwdt = duff(t,w,epsilon,F,omega)
x = w(1);
y = w(2);
dxdt = y;
dydt = - x - epsilon * x^3 + F * cos(omega*t);
dwdt = [dxdt;dydt];
end
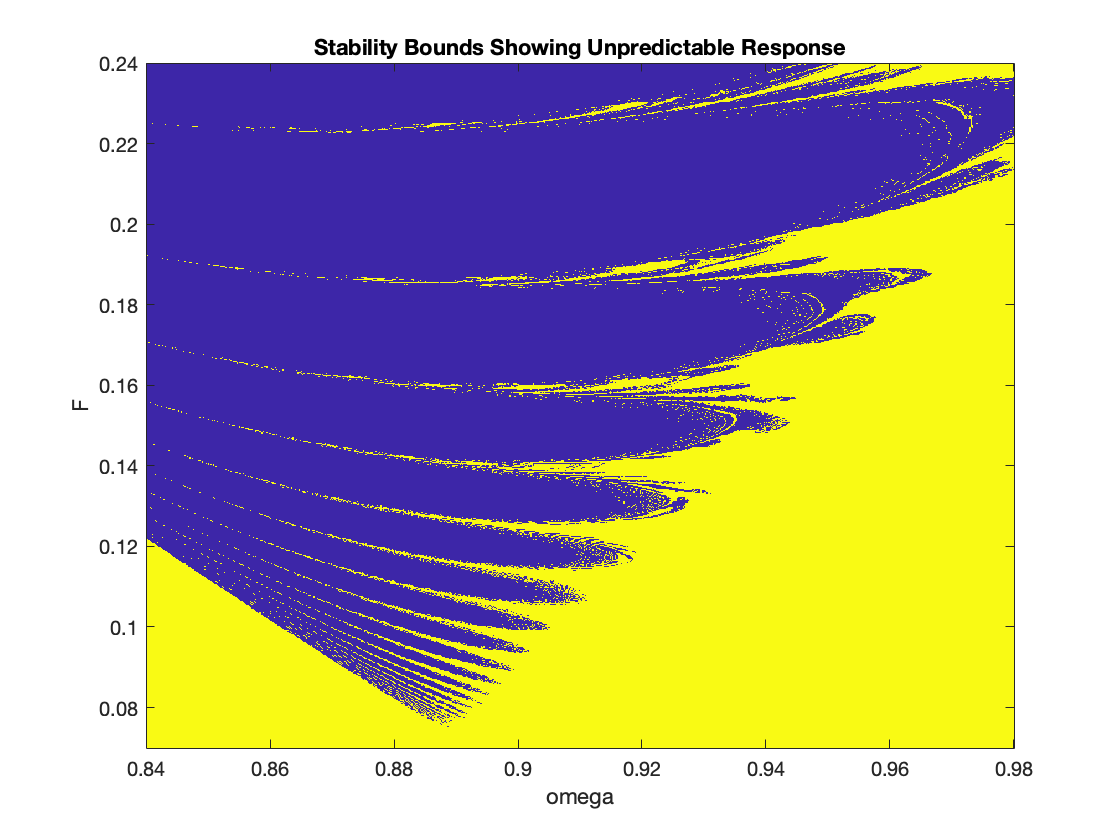
|
|
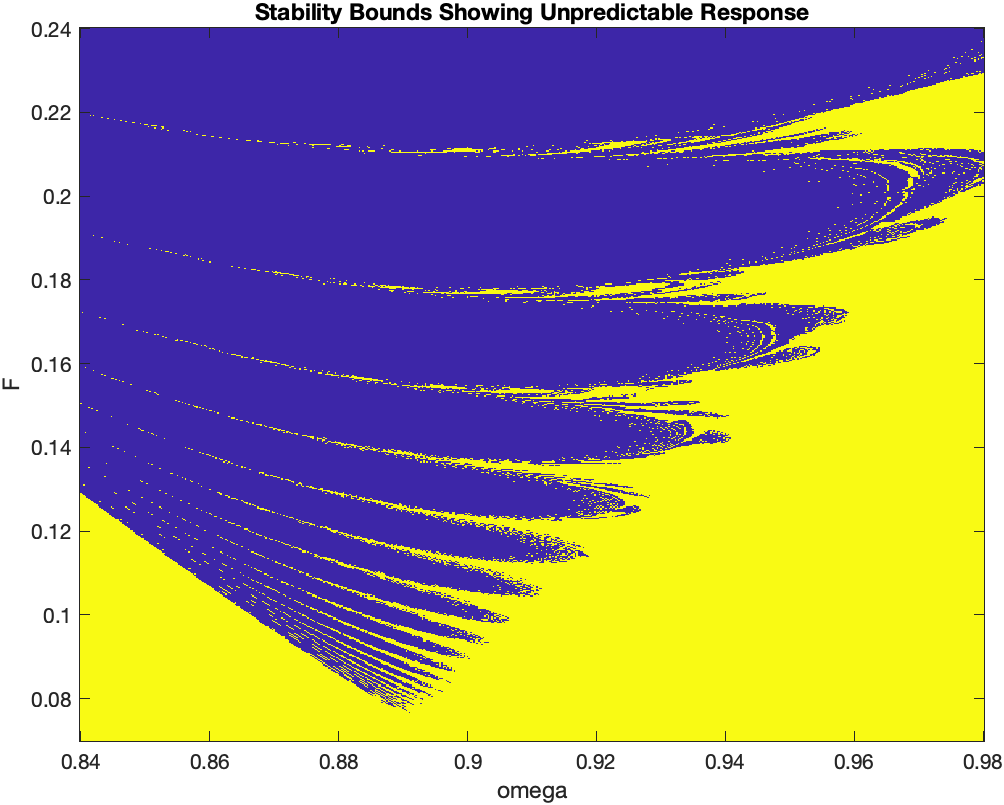
|
|
Forcing function: cos(ωt), 0.84 < ω < 0.98
|
|
Forcing function: sin(ωt), 0.84 < ω < 0.98
|
|
|
|
|
Forcing function: cos(ωt), 0 < ω < 4
|
|
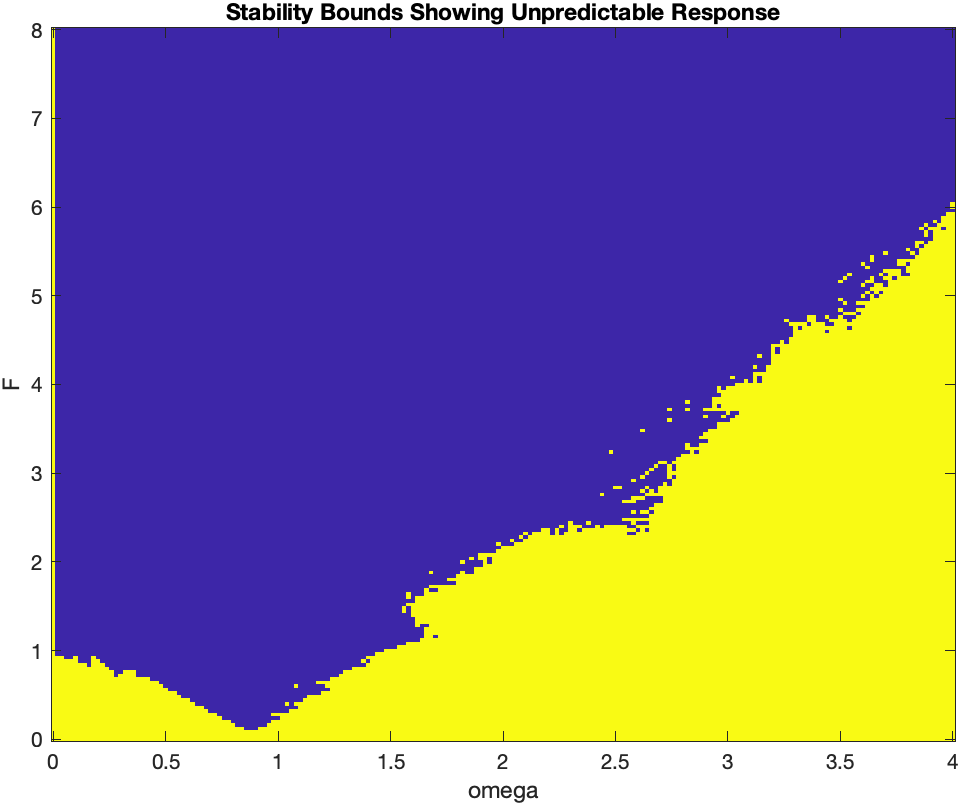
Forcing function: sin(ωt), 0 < ω < 4
|
|
|
|
|
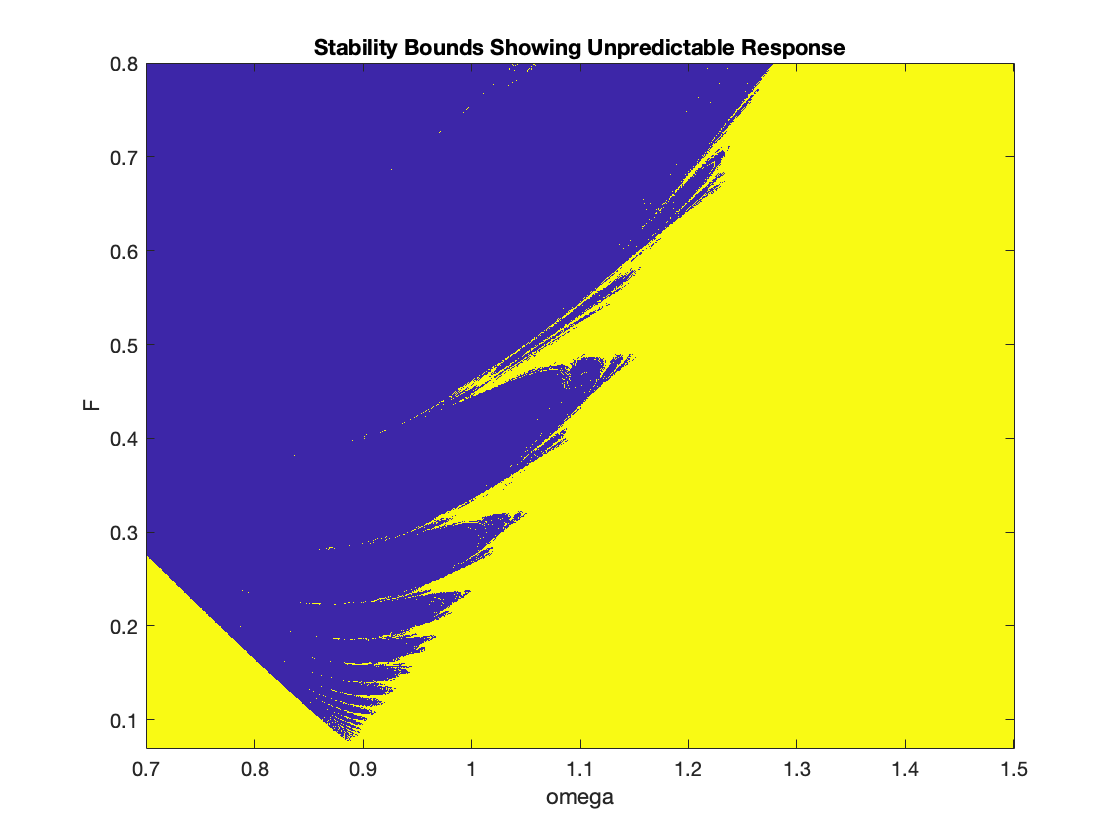
Forcing function: cos(ωt), 0.7 < ω < 1.5
|
|
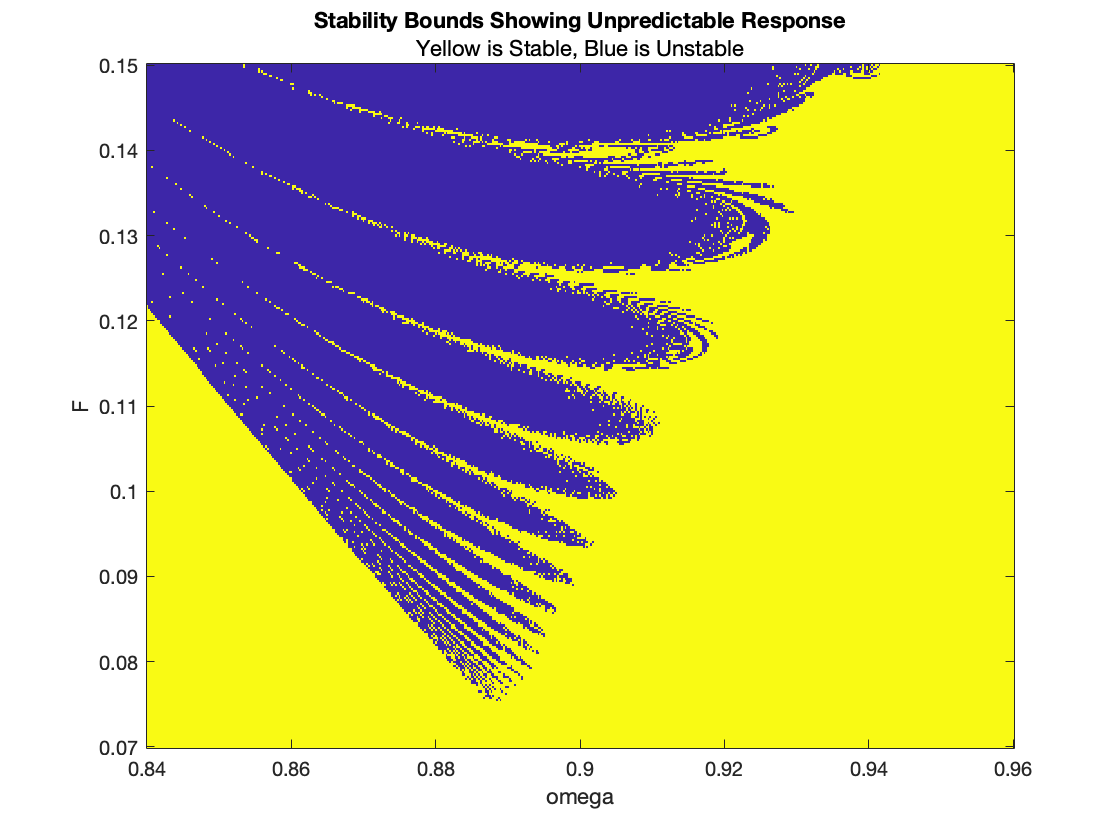
Forcing function: cos(ωt), 0.84 < ω < 0.98 & 0.07 < F < 0.15
|
-
Davis, H.T., Introduction to Nonlinear Differential and Integral Equations, 1962,
(New York: Dover Publications).
-
Duffing, G., 1918, Erzwungene Schwingungen bei veränderlicher Eigenfrequenz,
PhD Thesis, Braunschweig: Sammlung Vieweg.
-
Fay, T.H., Nonlinear resonance and Duffing's spring
equation, International Journal of Mathematical Education in
Science and Technology, 2006, Vol. 37, No. 5, pp. 593--599. https://doi.org/10.1080/00207390600594887
-
Fay
-
617.
-