Undamped simple pendulum:
|
|
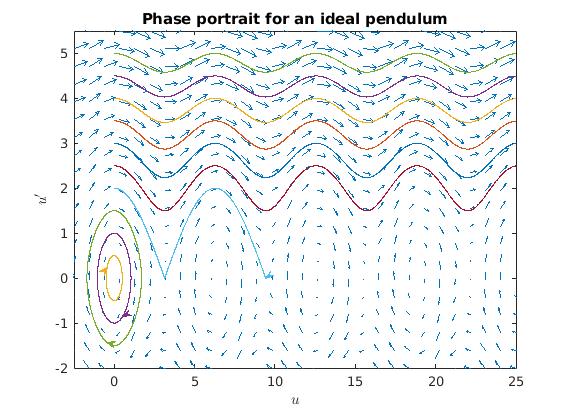
We plot the phase portrait of undamped ideal pendulum with Chebfun:
N = chebop(0, 50);
N.op = @(t,u) diff(u,2) + sin(u);
quiver(N, [-2.5 25 -2 5.5],'xpts',30)
hold on
for init = 0:0.5:5
N.lbc = [0, init];
u = N\0;
arrowplot(u, diff(u))
end
hold off
xlim([-2.5 25])
title('Phase portrait for an ideal pendulum')
xlabel('$u$',IN,LT), ylabel('$u''$',IN,LT)
|
We see that for small enough initial velocities, the pendulum swings back and forth around the equilibrium u=0, while for larger initial velocities, it swings over and over the top position. However, if we introduce damping, all trajectories will eventually end up at rest:
N.op = @(t,u) diff(u,2) + 0.25*diff(u) + sin(u);
quiver(N, [-2.5 25 -2 5.5],'xpts',30)
hold on
for init = 0:0.5:5
N.lbc = [0, init];
u = N\0;
plot(u, diff(u))
end
hold off
title('Phase portrait for a damped nonlinear pendulum')
xlabel('$u$',IN,LT), ylabel('$u''$',IN,LT)
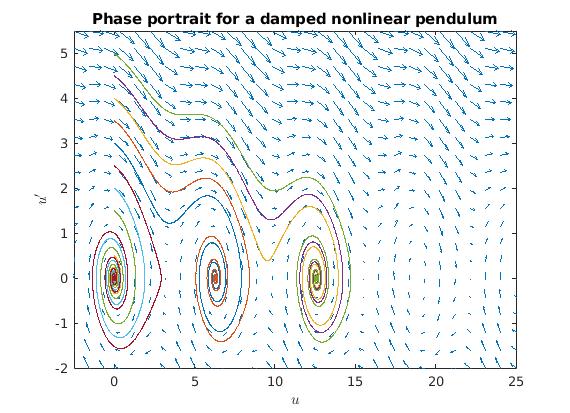Phas portrait for the damped pendulum, plotted with Chebfun.