There are known four kinds of Chebyshev polynomials that could be defined
through ordinary generating functions:
\begin{align}
\frac{1-xt}{1-2xt + t^2} &= \sum_{n\ge 0} T_n (x)\, t^n , \label{EqGF.1}
\\
\frac{1}{1-2xt + t^2} &= \sum_{n\ge 0} U_n (x)\, t^n , \label{EqGF.2}
\\
\frac{1-t}{1-2xt + t^2} &= \sum_{n\ge 0} V_n (x)\, t^n , \label{EqGF.3}
\\
\frac{1+t}{1-2xt + t^2} &= \sum_{n\ge 0} W_n (x)\, t^n . \label{EqGF.4}
\end{align}
However, the first two,
Tn and
Un, are
most popular because they are eigenfunctions of the following Sturm--Liouville
problems, respectively:
\begin{align*}
\left( 1 - x^2 \right) y'' - x\, y' + \lambda\,y &=0 , \qquad \lambda = n^2 ,
\\
\left( 1 - x^2 \right) y'' - 3x\, y' + \lambda\,y &=0 , \qquad \lambda =
n(n+2) .
\end{align}
Generating functions contain almost all information about Chebyshev polynomials, including explicit formulas and recurrence relations.
These polynomials could be defined "explicitly" either by the hypergeometric
series (which becomes a finite sum)
\begin{align*}
T_n (x) &= _2F_1 \left( -n, n, \frac{1}{2}; \frac{1-x}{2} \right) =
\frac{n}{2} \sum_{k=0}^{\left\lfloor \frac{n}{2} \right\rfloor}
\frac{(-1)^k}{n-k} \binom{n-k}{k} \left( 2x \right)^{n-2k} , \qquad n\ge 1,
\end{align*}
cos ( t ) = x
T(n,x) = cos ( n * t )
\begin{align*}
U_n (x) &= \left( n+1 \right) _2F_1 \left( -n, n+2, \frac{3}{2}; \frac{1-x}{2} \right) = \sum_{k=0}^{\left\lfloor \frac{n}{2} \right\rfloor}
(-1)^k \binom{n-k}{k} \left( 2x \right)^{n-2k} , \qquad n\ge 0,
\end{align*}
cos ( t ) = x
U(n,x) = sin ( ( n + 1 ) t ) / sin ( t )
\begin{align*}
V_n (x) &= _2F_1 \left( -n, n+1, \frac{1}{2}; \frac{1-x}{2} \right) =
\sum_{k=0}^{n}
(-1)^k \binom{2n-k}{k} 2^{n-k} \left( x-1 \right)^{n-k} , \qquad n\ge 0,
\end{align*}
cos ( t ) = x
V(n,x) = cos ( (2n+1)*t/2) / cos ( t/2)
\begin{align*}
W_n (x) &= \left( 2n+1 \right) _2F_1 \left( -n, n+1, \frac{3}{2};
\frac{1-x}{2} \right) = \left( 2n+1 \right) \sum_{k=0}^{n}
\frac{2^{n-k}}{2n-2k+1} \binom{2n-k}{k} \left( x-1 \right)^{n-k} ,
\qquad n\ge 0;
\end{align*}
cos ( t ) = x
W(n,x) = sin((2*n+1)*t/2)/sin(t/2)
or by Rodrigues' formulas:
\begin{align*}
T_n (x) &= \frac{(-1)^n 2^n n!}{(2n)!}\,\frac{{\text d}^n}{{\text d} x^n}
\left( 1- x^2 \right)^{n-1/2} ,
\\
U_n (x) &= \frac{(-1)^n 2^n (n+1)!}{(2n+1)!}\left( 1 - x^2 \right)^{-1}
\frac{{\text d}^n}{{\text d} x^n}
\left( 1- x^2 \right)^{n+1/2} ,
\\
\left( 1-x \right)^{-1/2} \left( 1+x \right)^{1/2} V_n (x) &=
\frac{(-1)^n 2^n n!}{(2n)!}\,\frac{{\text d}^n}{{\text d} x^n}
\left( 1- x \right)^{n-1/2} \left( 1+ x \right)^{n+1/2},
\\
\left( 1-x \right)^{1/2} \left( 1+x \right)^{-1/2} W_n (x) &=
\frac{(-1)^n 2^n n!}{(2n)!}\,\frac{{\text d}^n}{{\text d} x^n}
\left( 1- x \right)^{n+1/2} \left( 1+ x \right)^{n-1/2} .
\end{align*}
Chebyshev Polynomials of the First kind
Using
Mathematica, we find first Chebyshev polynomials of the first kind by expanding the generating function into Maclaurin series:
Series[(1 - x*t)/(1 - 2*x*t + t^2), {t, 0, 10}]
| n |
|
Chebyshev polynomial of the first kind |
| n = 0 |
|
T0(x) = 1 |
| n = 1 |
|
T1(x) = x |
| n = 2 |
|
T2(x) = 2x² −1 |
| n = 3 |
|
T3(x) = 4x³ −3x |
| n = 4 |
|
T4(x) = 8x4 −8x² + 1 |
| n = 5 |
|
T5(x) = 16x5 −20x³ + 5x |
| n = 6 |
|
T6(x) = 32x6 −48x4 + 18x² −1 |
| n = 7 |
|
T7(x) = 64x7 −112x5 + 56x³ −7x |
| n = 8 |
|
T8(x) = 27x8 −256x6 + 160x4 −32x² + 1 |
| n = 9 |
|
T9(x) = 28x9 −576x7 + 432x5 −120x³ + 9x |
| n = 10 |
|
T10(x) = 29x10 −1280x8 + 1120x6 −400x4 + 50x² − 1 |
Using Mathematica, we define the Chebyshev polynomials of the first kind from its generating function:
CT[n_, x_] :=
Module[{F, z, Dn}, F = ((1 - z^2)/(1 - 2*x*z + z^2) + 1)/2;
Dn = D[F, {z, n}];
Expand[Dn/n! /. z -> 0]]
|
|
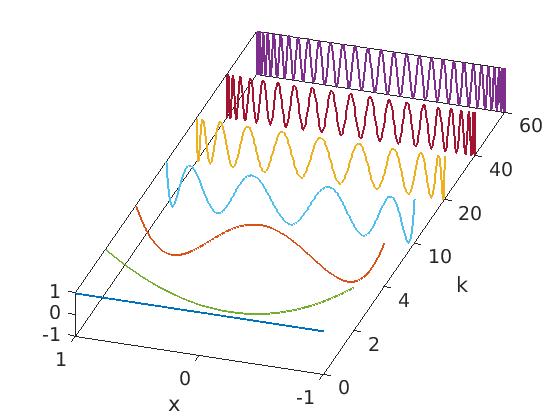
We plot with chebfun:
k = [0 2 4 10 20 40 60];
x = chebfun('x'); one = 1 + 0*x;
FS = 'fontsize'; fs = 14;
for j = 1:length(k)
plot3(j*one,x,chebpoly(k(j)),'linewidth',1.6), hold on
end
axis([1 length(k) -1 1 -1 1])
box on
set(gca,'dataaspectratio',[1 0.75 4]), view(-72,28)
set(gca,'xticklabel',k)
xlabel('k',FS,fs), ylabel('x',FS,fs), set(gca,FS,fs)
h = get(gca,'xlabel'); set(h,'position',get(h,'position')+[1.5 0.1 0])
h = get(gca,'ylabel'); set(h,'position',get(h,'position')+[0 0.25 0])
|
Chebyshev Polynomials of the Second kind
Using
Mathematica, we find first Chebyshev polynomials of the second kind by expanding the generating function into Maclaurin series:
Series[(1)/(1 - 2*x*t + t^2), {t, 0, 10}]
| n |
|
Chebyshev polynomial of the second kind |
| n = 0 |
|
U0(x) = 1 |
| n = 1 |
|
U1(x) = 2x |
| n = 2 |
|
U2(x) = 4x² −1 |
| n = 3 |
|
U3(x) = 8x³ −4x |
| n = 4 |
|
U4(x) = 16x4 −12x² + 1 |
| n = 5 |
|
U5(x) = 25x5 −32x³ + 6x |
| n = 6 |
|
U6(x) = 26x6 −80x4 + 24x² −1 |
| n = 7 |
|
U7(x) = 27x7 −192x5 + 80x³ −8x |
| n = 8 |
|
U8(x) = 28x8 −448x6 + 240x4 −40x² + 1 |
| n = 9 |
|
U9(x) = 29x9 −1024x7 + 672x5 −160x³ + 10x |
| n = 10 |
|
U10(x) = 210x10 −2304x8 + 1792x6 −560x4 + 60x² −1 |
Chebyshev Polynomials of the Third kind
Using
Mathematica, we find first Chebyshev polynomials of the third kind:
Series[(1 - t)/(1 - 2*x*t + t^2), {t, 0, 10}]
| n |
|
Chebyshev polynomial of the third kind |
| n = 0 |
|
V0(x) = 1 |
| n = 1 |
|
V1(x) = 2x − 1 |
| n = 2 |
|
V2(x) = 4x² − 2x −1 |
| n = 3 |
|
V3(x) = 8x³ − 4x² −4x + 1 |
| n = 4 |
|
V4(x) = 16x4 − 8x³ −12x² + 4x + 1 |
| n = 5 |
|
V5(x) = 32x5 − 16x4 −32x³ + 12x² + 6x − 1 |
| n = 6 |
|
V6(x) = 64x6 − 32x5 − 80x4 + 32x³ + 24x² − 6x −1 |
| n = 7 |
|
V7(x) = 27x7 − 64x6 −192x5 + 80x4 + 80x³ − 24x² −8x + 1
|
| n = 8 |
|
W8(x) = 28x8 − 27x7 −448x6 + 192x5 + 240x4 − 80x³ −40x² + 8x + 1
|
| n = 9 |
|
V9(x) = 29x9 − 28x8
− 210x7 + 448x6 + 672x5 − 240x4 − 160x³ + 40x² + 10x − 1
|
| n = 10 |
|
V10(x) = 210x10 − 29x9 − 2304x8
+ 210x7 + 1792x6 − 672x5 − 560x4 + 160x³ + 60x² − 10x − 1
|
Chebyshev Polynomials of the Fourth kind
Using
Mathematica, we find first Chebyshev polynomials of the fourth kind:
Series[(1 + t)/(1 - 2*x*t + t^2), {t, 0, 10}]
| n |
|
Chebyshev polynomial of the fourth kind |
| n = 0 |
|
W0(x) = 1 |
| n = 1 |
|
W1(x) = 1 + 2x |
| n = 2 |
|
W2(x) = 4x² + 2x −1 |
| n = 3 |
|
W3(x) = 8x³ +4x² −4x −1 |
| n = 4 |
|
W4(x) = 16x4 + 8x³ −12x² −4x + 1 |
| n = 5 |
|
W5(x) = 32x5 + 16x4 −32x³ −12x² + 6x + 1 |
| n = 6 |
|
W6(x) = 64x6 + 32x5 −80x4 −32x³ + 24x² + 6x −1 |
| n = 7 |
|
W7(x) = 27x7 + 64x6 −192x5 −80x4 + 80x³ + 24x² −8x −1
|
| n = 8 |
|
W8(x) = 28x8 + 27x7 −448x6 − 192x5 + 240x4 + 80x³ −40x² − 8x + 1
|
| n = 9 |
|
W9(x) = 29x9 + 28x8
− 210x7 −448x6 + 672x5 + 240x4 − 160x³ −40x² + 10x + 1
|
| n = 10 |
|
W10(x) = 210x10 + 29x9 − 2304x8
− 210x7 + 1792x6 + 672x5 − 560x4 − 160x³ + 60x² + 10x − 1
|
As we see from the table, the leading coefficient of Wn(x) is 2n.
-
Clenshaw, C.W., Norton, H.J.: The solution of nonlinear ordinary differential equations in chebyshev series. The Computer Journal, 1963, {\bf 6}, Issue 1, 88–92; https://doi.org/10.1093
-
-