MATLAB TUTORIAL, part 2.3: Pendulum

Pendulum
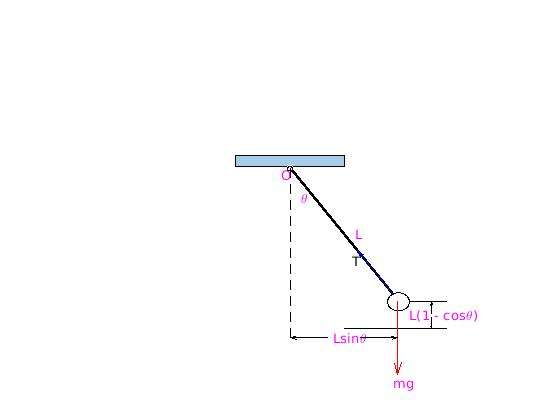
---> A simple pendulum consists of a single point of mass m (bob) attached to a rod (or wire) of length \( \ell \) and of negligible weight. We denote by θ the angle measured between the rod and the vertical axis, which is assumed to be positive in counterclockwise direction. We consider the simple pendulum that is characterized by the following assumptions:
  • The bob is free to move within a plane (so we consider only two-dimensional oscillations).
  • The system is conservative, so the pendulum rotates in a vacuum and friction in the pivot is negligible.
  • The bob of mass m is attached to one end of a rigid, but weightless rod of length ℓ, which is assumed to be constant during the pendulum motion. The other end of the rod (or rigid spring) is supported at the pivot.
      First, we illustrate with matlab the motion of the simple pendulum. Introducing the function f for circle arrow
       Figure 1: Simple pendulum.            matlab code

      The modeling of the motion is greatly simplified when the given body (bob) is considered essentially as a point particle. The position of the bob is described by the angle θ between the rod and the downward equilibrium vertical position, with the counterclockwise direction taken as positive. The only force acting on the pendulum is the gravitational force m g, acting downward, where g denotes the acceleration due to gravity. The position of the bob can be determined in Cartesian coordinates as
\[ x = \ell \,\sin \theta , \qquad y = -\ell\,\cos\theta , \]
where the origin is taken at the pivot and the positive vertical direction is upward. Using \( {\cal L} = \mbox{K} - \Pi , \) the Lagrangian, which is the difference of the kinetic energy K and the potential energy Π of the system, we have
\[ \frac{\text d}{{\text d}t} \,\frac{\partial {\cal L}}{\partial \dot{\theta}} = \frac{\partial {\cal L}}{\partial \theta} . \]

With the kinetic energy expressed via the angular displacement θ
\[ \mbox{K} = \frac{m}{2} \left( \dot{x}^2 + \dot{y}^2 \right) = \frac{m}{2}\, \ell^2 \left[ \left( \dot{\theta} \,\cos\theta \right)^2 + \left( \dot{\theta} \,\sin \theta \right)^2 \right] = \frac{m}{2}\,\ell^2 \dot{\theta}^2 . \]
and the potential energy
\[ \Pi = mg \left( \ell + y \right) = mg\ell \left( 1- \cos \theta \right) , \]
we derive the corresponding derivatives
\[ \frac{\partial \mbox{K}}{\partial \dot{\theta}} = I_0 \dot{\theta} = m\ell^2 \dot{\theta} , \qquad \frac{\partial \Pi}{\partial \theta} = mgy = mg\ell \, \sin \theta . \]
Using these expressions, we obtain from the Euler--Lagrange equation \( \displaystyle \frac{\text d}{{\text d} t} \left( \frac{\partial {\cal L}}{\partial \dot{\theta}} \right) = \frac{\partial {\cal L}}{\partial \theta} , \) for the Lagrangian \( {\cal L} = \mbox{K} - \Pi , \) the pendulum equation in a vacuum:
\[ \ddot{\theta} + \left( g/\ell \right) \sin \theta =0 \qquad \mbox{or} \qquad \ddot{\theta} + \omega_0^2 \sin \theta =0 \qquad \left( \omega_0^2 = g/\ell \right) , \]
where \( \ddot{\theta} = {\text d}^2 \theta / {\text d}t^2 \) , \( \omega_0 = \sqrt{g/\ell} >0 ,\) and g is gravitational acceleration.

Further simplification is available by normalization, which leads to \( \omega = 1 \) and we get

\[ \ddot{\theta} + \sin \theta =0 . \]
In practice, it is easier to study an ordinary differential equation as a system of equations involving only the first derivatives.
\[ \dot{x} = y, \qquad \dot{y} = -\sin x . \]
The variables x and y can be interpreted geometrically. Indeed, the angle x = θ corresponds to a point on a circle whereas the velocity \( y = \dot{\theta} \) corresponds to a point on a real line. Therefore, the set of all states (x ,y) can be represented by a cylinder, the product of a circle by a line. More formally, the phase space of the pendulum is the cylinder \( S^1 \times \mathbb{R} , \) its elements are couples (position,velocity).

Thus, at each point (x ,y) in the phase space, there is an attached vector \( (\dot{x}, \dot{y} ) = (y, - \sin x) . \) This can be geometrically represented as a vector field on the cylindrical phase space.

 

Example: The swinging mass m has a kinetic energy of \( m \ell^2 \left( {\text d}\theta /{\text d}t \right)^2 /2 \) and a potential energy of \( mg\ell\left( 1 - \cos \theta \right) ; \) the potential energy is zero for θ = 0. Let θM denote the maximum amplitude of the pendulum. Since dθ/dt = 0 at θ = θM, conservation of energy gives

\[ \frac{1}{2} \,m\ell^2 \left( \frac{{\text d}\theta}{{\text d}t} \right)^2 = mg\ell\,\cos \theta - mg\ell\,\cos \theta_M . \]
Solving for the velocity dθ/dt, we obtain
\[ \frac{{\text d}\theta}{{\text d}t} = \pm \left( \frac{2g}{\ell} \right)^{1/2} \left( \cos \theta - mg\ell\,\cos \theta_M \right)^{1/2} , \]
with the mass m canceling out. We take t to be zero, when θ = 0 and dθ/dt > 0. An integration from θ = 0 t0 θM yields
\begin{equation} \int_0^{\theta_M} \left( \cos \theta - mg\ell\,\cos \theta_M \right)^{-1/2} {\text d}\theta = \left( \frac{2g}{\ell} \right)^{1/2} \int_0^t {\text d}t = \left( \frac{2g}{\ell} \right)^{1/2} t . \label{pendulum.1} \end{equation}
This is one-fourth of a cycle, and therefore the time t is one-fourth of the period, T. We note that θ < θM, and with a bit of clairvoyance we try the half-angle substitution
\[ \sin \frac{\theta}{2} = \sin \left( \frac{\theta_M}{2} \right) \sin \phi . \]
With this, Eq.\eqref{pendulum.1} becomes
\begin{equation} T = 2\pi \left( \frac{\ell}{g} \right)^{1/2} \int_0^{\pi} \left[ 1 - \sin^2 \left( \frac{\theta_M}{2} \right) \sin^2 \phi \right]^{-1/2} {\text d}\phi . \label{pendulum.2} \end{equation}
Although not an obvious improvement over Eq.\eqref{pendulum.1}, the integral \eqref{pendulum.2} now defines the complete elliptic integral of the first kind,\( K \left( \sin^2 \theta_M /2 \right) . \) From the series expansion, the period of our pendulum may be developed as a power series—powers of sin θM/2:
\[ T = 2\pi \left( \frac{\ell}{g} \right)^{1/2} \left\{1 + \frac{1}{4}\,\sin^2 \frac{\theta_M}{2} + \frac{9}{64}\,\sin^4 \frac{\theta_M}{2} + \cdots \right\} . \]
   ■

 

Pendulum Equation with Resistance

 

We convert the pendulum equation with resistance
\[ m\ell^2 \ddot{\theta} + c\,\dot{\theta} + mg\ell \,\sin \theta =0 . \]
to a system of two first order equations by letting \( x= \theta \quad\mbox{and} \quad y = \dot{\theta} : \)
\[ \frac{{\text d} x}{{\text d}t} = y , \qquad \frac{{\text d} y}{{\text d}t} = -\omega^2 \sin x - \gamma \,y . \]
Here \( \gamma = c/(m\,\ell^2 ) , \ \omega^2 = g/\ell \) are positive constants. Therefore, the above system of differential equations is autonomous. Setting \( \gamma = 0.25 \quad\mbox{and}\quad \omega^2 =1 , \) we ask matlab to provide a phase portrait for the pendulum equation with resistance:

 

Pendulum with a ball

Let us consider a rod of length ℓ of mass m with attached ball of mass M at a distance L from the pivot.
     
rod = Graphics[{LightGray, Polygon[{{0.1, 0}, {0, 0.1}, {2.0, 2.1}, {2.1, 2.0}}]}];
ball = Graphics[{Orange, Disk[{1.75, 1.75}, 0.25]}];
ar3 = Graphics[{Black, Dashed, Thickness[0.01], Arrowheads[0.08], Arrow[{{1, 1}, {1, 0.4}}]}];
ar = Graphics[{Black, Thickness[0.01], Arrowheads[0.08], Arrow[{{-0.2, 0}, {2.5, 0}}]}];
ar2 = Graphics[{Black, Dashed, Thickness[0.01], Arrowheads[0.08], Arrow[{{0, -0.2}, {0, 2.2}}]}];
tl = Graphics[{Black, Text[Style["\[ScriptL]", 18, FontFamily -> "Mathematica1"], {1.2, 1.45}]}];
tx = Graphics[{Black, Text[Style["x", 18], {2.4, 0.2}]}];
tm = Graphics[{Black, Text[Style["M", 18, FontFamily -> "Mathematica1"], {1.4, 1.75}]}];
t1 = Graphics[{Black, Text[Style["C", 18], {1.0, 1.2}]}];
t2 = Graphics[{Black, Text[Style["\[Theta]", 18], {0.15, 0.4}]}];
t3 = Graphics[{Black, Text[Style["mg", 18], {1.05, 0.3}]}];
Show[rod, ar, ar2, ar3, tx, tl, tm, t1, t2, t3, ball]
       Rigid pendulum with a ball.            Mathematica code

To analyze the problem of falling meterstick of length ℓ with attached heavy weight at a distance L from the pivot, we use the tourque equation:
\[ I\,\ddot{\theta} = \tau \]
is the torque. This yields
\[ I\,\ddot{\theta} = \left( \frac{m}{2}\,g\,\ell + Mg\,L \right) \sin\theta , \]
where θ = θ(t) is the instanteneous angle of the rod with the vertical axis, and \( \displaystyle I = \frac{m}{3}\,\ell^2 + M\,L^2 \) is the moment of inertia about the lower end. Introducing the dimensionless ratios k = M/m and q = L/ℓ, we can express the angular acceleration of the loaded stick in terms of the angular acceleration of the bare meterstick and a dimensionless factor:
\[ \ddot{\theta} = \frac{3g}{2\ell}\cdot \frac{1 + 2kq}{1 + kq^2} \cdot \sin\theta . \]
It is instructive to examine the dimensionless factor in the previous equation of motion. For q = ⅔, it equals 1 for all values of k. Adding any point mass at ⅔ of the length ℓ of a uniform rod leaves the angular acceleration and, therefore, the time of fall unchanged. For q < ⅔, the factor becomes greater than 1, and the time of fall gets shorter. The opposite is true for q > ⅔. k*

 

Spherical Pendulum

Consider the motion under gravity of a bob of mass m attached to a fixed point by an inextensible massless rod of length ℓ. The bob is free to move on a sphere of radius ℓ. Using spherical coordinates (angles) θ and ϕ as the generalized coordinates, the kinetic and potential energies become
\begin{align*} \mbox{K} &= \frac{m}{2}\,\ell^2 \left( \dot{\theta}^2 + \dot{\phi}^2 \sin^2 \theta \right) , \\ \Pi &= mg\ell \left( 1- \cos \theta \right) . \end{align*}
This allows us to derive the Euler--Lagrange equations for the corresponding Lagrangian:
\[ \frac{\text d}{{\text d}t} \left( \frac{\partial {\cal L}}{\partial \dot{\theta}} \right) - \frac{\partial {\cal L}}{\partial \theta} = 0 , \qquad \frac{\text d}{{\text d}t} \left( \frac{\partial {\cal L}}{\partial \dot{\phi}} \right) - \frac{\partial {\cal L}}{\partial \phi} = 0 . \]
Substituting the expressions for the kinetic and potential energies, we obtain two coupled equations
\[ \begin{split} \ddot{\theta} + \frac{g}{\ell} \,\sin\theta - \frac{1}{2} \,\dot{\phi}^2 \sin 2\theta &= 0, \\ \ddot{\phi}\,\sin\theta + 2\dot{\phi} \dot{\theta}\,\cos\theta &= 0. \end{split} \]
The last equation is a first order differential equation with respect to the derivative of ϕ, so it can be integrated
\[ \dot{\phi} \sin^2 \theta = c, \quad \mbox{a constant}. \]
Using this equation, we obtain the following differential equation for nagle θ:
\[ \dot{\theta} + \frac{g}{\ell} \,\sin\theta - \frac{c^2 \cos\theta}{\sin^3 \theta} = 0. \]

 

Pendulum with moving support

The length of the pendulum is increasing by stretching of the wire due to the weight of the bob. The effective spring constant for a wire of rest length \( \ell_0 \) is

\[ k = ES/ \ell_0 , \]
where the elastic modulus (Young's modulus) for steel is about \( E \approx 2.0 \times 10^{11} \) Pa and S is the cross-sectional area. With pendulum 3 m long, the static increase in elongation is about \( \Delta \ell = 1.6 \) mm, which is clearly not negligible. There is also dynamic stretching of the wire from the apparent centrifugal and Coriolis forces acting on the bob during motion. We can evaluate this effect by adapting a spring-pendulum system analysis. WE go from rectangular to polar coordinates:
\[ x= \ell \,\sin \theta = z_0 \left( 1 + \xi \right) \sin \theta , \qquad z= z_0 - \ell\,\cos \theta = z_0 \left[ 1 - \left( 1 + \xi \right) \cos \theta \right] , , \]
where \( z_0 = \ell_0 + mg/k \) is the static pendulum length, \( \ell = z_0 \left( 1 + \xi \right) \) is the dynamic length, ξ is the fractional string extension, and θ is the deflection angle. the equations of motion for small deflections are
\begin{eqnarray*} \left( 1 + \xi \right)\ddot{\theta} + 2\dot{\theta}\,\dot{\xi} + \omega_p^2 \theta &=& 0 , \\ \ddot{\xi} + \omega_s^2 \xi - \dot{\theta} + \frac{1}[2}\,\omega_p^2 \theta^2 &=& 0, \end{equarray*}
where the overdots denote differentiation with respect to time t, \( \omega_p^2 = g/z_0 \) is the square of the pendulum frequency, and \( \omega_s^2 = k/m \) is the spring (string) frequency, squared.

To get a feeling for how rigid and massive the pendulum support must be, we model the support as mass M kept in place by a spring of constant K, as shown in the picture below.

p = Rectangle[{-Pi/6 - 1.2, 2}, {-5, -5}]
a = Graphics[{Gray, p}]
coil = ParametricPlot[{t + 1.2*Sin[3*t], 1.2*Cos[3*t] - 1.2}, {t, -Pi/6 , 5*Pi - Pi/6}, FrameTicks -> None, PlotStyle -> Black]
line = Graphics[{Thick, Line[{{16.3843645, -1.2}, {20, -1.2}}]}]
r = Graphics[{EdgeForm[{Thick, Blue}], FaceForm[], Rectangle[{20, -5}, {26, 2}]}]
back = RegionPlot[-5 < x < 28 || -7 < y < -5, {x, -5, 28}, {y, -7, -5}, PlotStyle -> LightOrange]
line2 = Graphics[{Thick, Dashed, Line[{{23, -1}, {23, -14}}]}]
line3 = Graphics[{Thick, Line[{{23, -1}, {29, -11.5}}]}]
disk = Graphics[{Pink, Disk[{29.5, -12}, 1]}]
text = Graphics[Text["\[Theta]" , {25.1, -9.5}]]
Show[a, coil, line, r, back, line2, line3, disk, text]
Pendulum with moving support.

The natural frequency of the support is

\[ \Omega = \left( K/M \right)^{1/2} . \] The coupled equations for the system are
\begin{eqnarray*} \ddot{\theta} + \omega_0^2 \theta + \ddot{x}/\ell &=& 0 , \\ \left( 1 + m/M \right) \ddot{x} + \left( m/M \right) \ell \,\ddot{\theta} + \Omega^2 x &=& 0, \end{eqnarray*}
where x is the displacement of the rigid support. The former equation says that the effect of sway is to impart an additional angular acceleration \( - \ddot{x}/\ell \) to the pendulum for small angles of oscillation (otherwise, we have to use \( \omega_0^2 \sin \theta \) instead of \( \omega_0^2 \theta \) ).

 

Spring Pendulum


function main
tstart=0;
tstop=20;
z0=0; z0prime=1; theta0=0.1; theta0prime=0.1;
initial_w=[z0, theta0,z0prime,theta0prime]
k=50 ; m=2;  g=9.81;
l=0.5+m*g/k;
[times,sols]=ode45(@(t,w) diffeq(t,w,k,m,l,g), [tstart,tstop],initial_w)

figure
comet(sols(:,1),sols(:,2))
title('Theta vs z')
xlabel('z'),ylabel('theta (rad)')

figure
comet((times),sols(:,1))
title('z vs time')
xlabel('time'),ylabel('z')

figure
comet((times),sols(:,2))
title('Theta vs time')
xlabel('time'),ylabel('theta (rad)')

end
function dwdt=diffeq(t,w,k,m,l,g)
u1=w(1); u2=w(3); v1=w(2); v2=w(4);
du1dt=u2;
du2dt=-k/m*u1-g/(2*l)*v1^2+v2^2;
dv1dt=v2;
dv2dt=1/(1+2*u1)*(-g/l*v1-g/l*u1*v1-2*u2*v2);
dwdt=[du1dt;dv1dt;du2dt;dv2dt];



function spring

%Initial Conditions
initial_w=[0;0.1;1.5;0.1];
m=.2; k=5; g=9.8; l=.5+(m*g/k);

%Solves differential equation
[time,sols]=ode45(@(t,w) diffeq(t,w,m,k,g,l),[0,20],initial_w) %column 1 of solutions is z(t), column 2 is theta(t), column 3 is z'(t), column 4 is theta'(t)
%Plots path
figure
comet(sols(:,1),sols(:,2)) %Plots z vs theta
title('Displacement vs Theta')
xlabel('Theta (rad)')
ylabel('Displacement')

figure
comet(time,sols(:,1)) %Plots z vs time
title('Displacement vs Time')
xlabel('Time (s)')
ylabel('Displacement')

figure
comet(time,sols(:,2)) %Plots theta vs time
title('Theta vs Time')
xlabel('Time (s)')
ylabel('Theta (rad)')

end
function dwdt = diffeq(t,w,m,k,g,l)
z=w(1); theta=w(2); vz=w(3); vtheta=w(4) %Assigns values from vector w
dzdt=vz; dthetadt=vtheta;

dvzdt=-((k/m)*z + (g/(2*l))*theta^2 - vtheta^2)
dvthetadt= -((g/l)*theta + (g/(2*l))*z*theta + 2*vz*vtheta)/(1+2*z)

dwdt=[dzdt;dthetadt;dvzdt;dvthetadt]; %Puts derivatives into matrix dwdt

end

 

Double Pendulum

Double pendulum.
Double compound pendulum.
Animation of double pendulum.

A double pendulum consists of one pendulum attached to another. Double pendula are an example of a simple physical system which can exhibit chaotic behavior with a strong sensitivity to initial conditions. Several variants of the double pendulum may be considered; the two limbs may be of equal or unequal lengths and masses, they may be simple pendulums/pendula or compound pendulums (also called complex pendulums) and the motion may be in three dimensions or restricted to the vertical plane.

Consider a double bob pendulum with masses m1 and m2 attached by rigid massless wires of lengths \( \ell_1 \) and \( \ell_2 . \) Further, let the angles the two wires make with the vertical be denoted \( \theta_1 \) and \( \theta_2 , \) as illustrated at the left. Let the origin of the Cartesian coordinate system is taken to be at the point of suspension of the first pendulum, with vertical axis pointed up. Finally, let gravity be given by g. Then the positions of the bobs are given by

\begin{eqnarray*} x_1 &=& \ell_1 \sin \theta_1 , \\ y_1 &=& -\ell_1 \cos \theta_1 , \\ x_2 &=& \ell_1 \sin \theta_1 + \ell_2 \sin \theta_2 , \\ y_2 &=& -\ell_1 \cos \theta_1 - \ell_2 \cos \theta_2 . \end{eqnarray*}
The potential energy of the system is then given by
\[ \Pi = g\, m_1 \left( \ell_1 + y_1 \right) + g\,m_2 \left( \ell_1 + \ell_2 + y_2 \right) = g\,m_1 \left( 1- \cos \theta_1 \right) + g\, m_2 \left( \ell_1 + \ell_2 - \ell_1 \cos \theta_1 - \ell_2 \cos \theta_2 \right) , \]
and the kinetic energy by
\begin{eqnarray*} \mbox{K} &=& \frac{1}{2}\, m_1 v_1^2 + \frac{1}{2}\, m_2 v_2^2 \\ &=& \frac{1}{2}\, m_1 \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2}\, m_2 \left[ \ell_1^2 \dot{\theta}_1^2 + \ell_2^2 \dot{\theta}_2^2 +2\ell_1 \ell_2 \dot{\theta}_1 \dot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) \right] \end{eqnarray*}
because
\[ v_1^2 = \dot{x}_1^2 + \dot{y}_1^2 = \ell_1^2 \dot{\theta}_1^2 , \qquad v_2^2 = \dot{x}_2^2 + \dot{y}_2^2 = \left( \ell_1 \cos\theta_1 \,\dot{\theta}_1 + \ell_2 \cos \theta_2 \,\dot{\theta}_2 \right)^2 + \left( \ell_1 \sin\theta_1 \,\dot{\theta}_1 + \ell_2 \sin \theta_2 \,\dot{\theta}_2 \right)^2 . \]
The Lagrangian is then
\begin{eqnarray*} {\cal L} &=& \mbox{K} - \Pi \\ &=& \frac{1}{2}\, m_1 \ell_1^2 \dot{\theta}_1^2 + \frac{1}{2}\, m_2 \left[ \ell_1^2 \dot{\theta}_1^2 + \ell_2^2 \dot{\theta}_2^2 +2\ell_1 \ell_2 \dot{\theta}_1 \dot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) \right] + \left( m_1 + m_2 \right) g\ell_1 \cos \theta_1 + m_2 g \ell_2 \cos \theta_2 . \end{eqnarray*}
Therefore, for θ1 we have
\begin{eqnarray*} \frac{\partial {\cal L}}{\partial \dot{\theta}_1} &=& m_1 \ell_1^2 \dot{\theta}_1 + m_2 \ell_1^2 \dot{\theta}_1 + m_2 \ell_1 \ell_2 \dot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) , \\ \frac{{\text d}}{{\text d}t} \left( \frac{\partial {\cal L}}{\partial \dot{\theta}_1} \right) &=& \left( m_1 + m_2 \right) \ell_1^2 \ddot{\theta}_1 + m_2 \ell_1 \ell_2 \ddot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) - m_2 \ell_1 \ell_2 \dot{\theta}_2 \sin \left( \theta_1 - \theta_2 \right) \left( \dot{\theta}_1 - \dot{\theta}_2 \right) , \\ \frac{\partial {\cal L}}{\partial \theta_1} &=& - \ell_1 g \left( m_1 + m_2 \right) \sin \theta_1 - m_2 \ell_1 \ell_2 \dot{\theta}_1 \dot{\theta}_2 \sin \left( \theta_1 - \theta_2 \right) . \end{eqnarray*}
So the Euler-Lagrange differential equation \( \frac{{\text d}}{{\text d}t} \left( \frac{\partial {\cal L}}{\partial \dot{q}} \right) = \frac{\partial {\cal L}}{\partial q} \) for θ1 becomes
\[ \left( m_1 + m_2 \right) \ell_1^2 \ddot{\theta}_1 + m_2 \ell_1 \ell_2 \ddot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) + m_2 \ell_1 \ell_2 \dot{\theta}_2^2 \sin \left( \theta_1 - \theta_2 \right) + \ell_1 g \left( m_1 + m_2 \right) \sin \theta_1 =0 . \]
Dividing through by \( \ell_1 , \) this simplifies to
\[ \left( m_1 + m_2 \right) \ell_1 \ddot{\theta}_1 + m_2 \ell_2 \ddot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) + m_2 \ell_2 \dot{\theta}_2^2 \sin \left( \theta_1 - \theta_2 \right) + g \left( m_1 + m_2 \right) \sin \theta_1 =0 . \]
Similarly, for θ2, we have
\begin{eqnarray*} \frac{\partial {\cal L}}{\partial \dot{\theta}_2} &=& m_2 \ell_2^2 \dot{\theta}_2 + m_2 \ell_1 \ell_2 \dot{\theta}_1 \cos \left( \theta_1 - \theta_2 \right) , \\ \frac{{\text d}}{{\text d}t} \left( \frac{\partial {\cal L}}{\partial \dot{\theta}_2} \right) &=& m_2 \ell_2^2 \ddot{\theta}_2 + m_2 \ell_1 \ell_2 \ddot{\theta}_1 \cos \left( \theta_1 - \theta_2 \right) - m_2 \ell_1 \ell_2 \dot{\theta}_1 \sin \left( \theta_1 - \theta_2 \right) \left( \dot{\theta}_1 - \dot{\theta}_2 \right) , \\ \frac{\partial {\cal L}}{\partial \theta_2} &=& \ell_1 \ell_2 m_2 \dot{\theta}_1 \dot{\theta}_2 \sin \left( \theta_1 - \theta_2 \right) - \ell_2 m_2 g\,\sin \theta_2 , \end{eqnarray*}
which leads to
\[ m_2 \ell_2 \ddot{\theta}_2 + m_2 \ell_1 \ddot{\theta}_1 \cos \left( \theta_1 - \theta_2 \right) - m_2 \ell_1 \dot{\theta}_1^2 \sin \left( \theta_1 - \theta_2 \right) + m_2 g \, \sin \theta_2 =0 . \]
The coupled second-order ordinary differential equations
\begin{eqnarray*} \left( m_1 + m_2 \right) \ell_1 \ddot{\theta}_1 + m_2 \ell_2 \ddot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) + m_2 \ell_2 \dot{\theta}_2^2 \sin \left( \theta_1 - \theta_2 \right) + g \left( m_1 + m_2 \right) \sin \theta_1 &=& 0 , \\ m_2 \ell_2 \ddot{\theta}_2 + m_2 \ell_1 \ddot{\theta}_1 \cos \left( \theta_1 - \theta_2 \right) - m_2 \ell_1 \dot{\theta}_1^2 \sin \left( \theta_1 - \theta_2 \right) + m_2 g \, \sin \theta_2 &=& 0 \end{eqnarray*}

The equations of motion can also be written in the Hamiltonian formalism. Computing the generalized momenta gives

\begin{eqnarray*} p_1 &=& \frac{\partial {\cal L}}{\partial \dot{\theta}_1} = \left( m_1 + m_2 \right) \ell_1^2 \dot{\theta}_1 + m_2 \ell_1 \ell_2 \dot{\theta}_2 \cos \left( \theta_1 - \theta_2 \right) , \\ p_2 &=& \frac{\partial {\cal L}}{\partial \dot{\theta}_2} = m_2 \ell_2^2 \dot{\theta}_2 + m_2 \ell_1 \ell_2 \dot{\theta}_1 \cos \left( \theta_1 - \theta_2 \right) . \end{eqnarray*}
The Hamiltonian becomes
\[ H = \dot{\theta}_1 p_1 + \dot{\theta}_2 p_2 - {\cal L} . \]
For animationof double pendulum equations, see:
https://www.myphysicslab.com/pendulum/double-pendulum-en.html 

function DoublePendulum
  [l1,l2,~,~,~,s]=pendata;  % parameters
  ax1=[-s s -s s]; % vector for axes
  T = 25; % Process duration, s
  v = 3;  % Speed of animation, positive integer: 1, 2, 3,...
% Initial values
  theta1_1 = pi/2;
  theta1 = 0;
  theta2_1 = pi/2;
  theta2 = 0;
  y0 = [theta1_1, theta1, theta2_1, theta2];

  [t,y] = ode45(@Equations, [0, T], y0);
  x1 = l1*sin(y(:,1));
  y1 = -l1*cos(y(:,1));
  x2 = x1 + l2*sin(y(:,3));
  y2 = y1 - l2*cos(y(:,3));

  figure
  tic
%   Animation
  for i = 1:v:numel(t)
   plot(0, 0,'k.',x1(i),y1(i),'b.',x2(i),y2(i),'r.','markersize',40);
   axis(ax1)
   line([0 x1(i)], [0 y1(i)],'Linewidth',2);
   line([x1(i) x2(i)], [y1(i) y2(i)],'linewidth',2,'color','r');
   xlabel(['\it\bf X \rm        Animation time, s:  ',num2str(toc,3)],...
     'HorizontalAlignment', 'left');
   ylabel('\it\bf Y');
   title(['Double Pendulum       \it t \rm= ',num2str(t(i),3)],...
     'fontsize',13, 'HorizontalAlignment', 'left', 'Position',[-.4*s s 0])
   drawnow
  end

%   Graphs
  figure
  plot(x1,y1,x2,y2,'r')
  xlabel('\it X','fontSize',12);
  ylabel('\it Y','fontSize',12);
  title('Chaotic Motion of a Double Pendulum')

  figure
  plot(t,y(:,1),t,y(:,3),'r','linewidth',2)
  axis([0,T,min(y(:,3)),max(y(:,3))])
  legend('\theta_1','\theta_2')
  xlabel('Time, s','fontSize',12)
  ylabel('\theta','fontSize',18,'fontweight','bold')
  title('\theta_1(0) = \pi/2  and  \theta_2(0) = \pi/2','fontsize',13)
 end

function z = Equations(~, y)
  [l1,l2,m1,m2,g,~]=pendata;
  z(4,1)=0;
  a = (m1+m2)*l1 ;
  b = m2*l2*cos(y(1)-y(3)) ;
  c = m2*l1*cos(y(1)-y(3)) ;
  d = m2*l2 ;
  e = -m2*l2*y(4)* y(4)*sin(y(1)-y(3))-g*(m1+m2)*sin(y(1)) ;
  f = m2*l1*y(2)*y(2)*sin(y(1)-y(3))-m2*g*sin(y(3)) ;

  z(1) = y(2);
  z(3) = y(4) ;
  z(2) = (e*d-b*f)/(a*d-c*b) ;
  z(4) = (a*f-c*e)/(a*d-c*b) ;
end

function [l1,l2,m1,m2,g,s] = pendata
  l1 = .3;  % length of the upper part of the double pendulum, m
  l2 = .3;  % length of the lower part of the double pendulum, m
  m1 = .1;  % mass of the upper part of the double pendulum, kg
  m2 = .1;  % mass of the lower part of the double pendulum, kg
  g = 9.8;  % gravitational acceleration, m/s^2
  s = l1+l2;
end



Complete