The determinant is a special scalar-valued function defined on the set of square matrices. Although it still has a place in many areas of mathematics and physics, our primary application of determinants is to define eigenvalues and characteristic polynomials for a square matrix A. It is usually denoted as det(A), det A, or |A|. The term determinant was first introduced by the German mathematician Carl Friedrich Gauss in 1801. There are various equivalent ways to define the determinant of a square matrix A, i.e., one with the same number of rows and columns. The determinant of a matrix of arbitrary size can be defined by the Leibniz formula or the Laplace formula (see next section).

Determinants

Because of difficulties with motivation, intuitiveness, and simple definition, there is a tendency in exposition of linear algebra without classical involvement of determinants (see {1,2]). Since we respect both approaches, the tutorial presents several definitions of determinants. One of popular approaches is to define a determinant of a square matrix as a product of all its eigenvalues (which is a topic of next section), counting multiplicities. If the reader wants to follow this easy to remember definition, then the order of reading sections should be changed or we refer to S. Axler's textbook. It should be noted that both approaches still wait for efficient numerical algorithms. Now almost all computational software packages evaluate the determinant in O(n3) arithmetic operations by forming the LU decomposition. We start with non-constructive definition of determinant.

A functional δ from the set of all n×n matrices into the field of scalars is called an n-linear or multilinear if it is a linear map of each row or each column of any n×n matrix when the remaining n-1 rows/columns are held fixed. Such functional is called alternating if for each square matrix A, we have δ(A) = 0 whenever two adjacent rows (or columns) of A are identical.
An alternating multilinear functional such that δ(I) = 1, where I is the identity matrix, is called the determinant and is denoted as det(A) or detA, or just |A|.
Now we give two "constructive" definitions of determinants---one is called the Leibniz formula and another one, the Laplace cofactor expansion (next section is dedicated to this definition).
For any indexing set n = [ 1, 2, ..., n ], a permutation of n is a one-to-one and onto function π: n ↦ n.

An inversion in a permutation π is any pair (i,j) ∈ n × n for which i < j and π(i) > &pi(j).

A permutation is called even if it has an even number of inversions and odd otherwise.

The Leibniz formula for the determinant of an n × n matrix A is
\[ \det\left( {\bf A} \right) = \sum_{\sigma\in S_n} \left( \mbox{sign} (\sigma ) \,\prod_{i=1}^n a_{i, \sigma_i} \right) , \]
where sign is the sign function of permutations in the permutation group Sn, which returns +1 and −1 for even and odd permutations, respectively. Here the sum is computed over all permutations σ of the set {1, 2, …, n}. A permutation is a function that reorders this set of integers. The value in the i-th position after the reordering σ is denoted by σi.

Theorem 1: Let V be a vector space and let μ be an alternation n-linear functional. If σ is a permutation of the first n integers, then \[ \mu \left( {\bf v}_{\sigma (1)} , \ {\bf v}_{\sigma (2)} , \ \ldots , \ {\bf v}_{\sigma (n)} \right) = \mbox{sign} \left( \sigma \right) \mu \left( {\bf v}_{1}, \ {\bf v}_{2}, \ \ldots , \ {\bf v}_{n} \right) . \]

Let V and μ be as hypothesized. As an alternating map, μ is skew- symmetric so if τ in Sk is a transposition, then \[ \mu \left( {\bf v}_{\tau (1)} .\ {\bf v}_{\tau (2)} , \ \ldots , \ {\bf v}_{(k)} \right) = - \mu \left( {\bf v}_1 .\ {\bf v}_2 , \ \ldots , \ {\bf v}_k \right) . \] The result follows from the fact that every permutation is a product of transpositions.

The Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |A| of an n × n matrix A that is a weighted sum of the determinants of n sub-matrices of A, each of size (n−1) × (n−1). The Laplace expansion (which we discuss in the next section) as well as the Leibniz formula are of theoretical interest as one of several ways to view the determinant, but not for practical use in determinant computation.

Determinants are used to determine the volumes of parallelepipeds formed by n vectors in n-dimensional Euclidean space. In 2 and 3 dimensional cases, the determinant is the area of parallelogram and the volume of parallelepiped, respectively. We plot them with Mathematica

p = {0, 0};
v1 = {1, 2};
v2 = {1, 0};
ill = {Black, PointSize[Large], Point[p], Arrowheads[Medium], Thick, Arrow[{p, v1}], Arrow[{p, v2}]};
par = Graphics[{Pink, Parallelogram[p, {v1, v2}], ill}]
txt1 = Graphics[ Text[Style["(a,b)", FontSize -> 14, Black], {1.2, 0.05}]];
txt2 = Graphics[ Text[Style["(c,d)", FontSize -> 14, Black], {0.8, 2.0}]];
txt3 = Graphics[ Text[Style["(a+c, b+d)", FontSize -> 14, Black], {2.1, 2.1}]];
txt4 = Graphics[ Text[Style["ad-bc", FontSize -> 16, Black], {1.0, 1.0}]];
Show[par, txt1, txt2, txt3, txt4]
and
Graphics3D[ Parallelepiped[{0, 0, 0}, {{1, 0, 0}, {2, 1, 0}, {0, 1, 1}}]]
The area of the parallelogram
The volume of the parallelepiped
The n-volume of an n-parallelepiped formed by n vectors in ℝn is the absolute value of the determinant of these n vectors. When a square matrix A is considered as a transformation ℝn ↦ ℝn, the absolute value of its determinant is called the magnification factor because it the volume of the image of the unit n-cube.

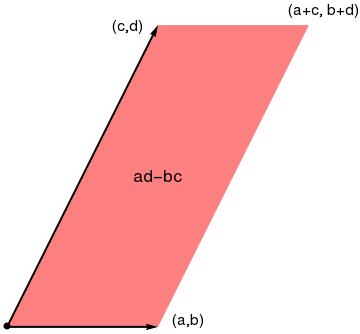
The Leibniz formula for the determinant of a 2 × 2 matrix is

\[ \left\vert \begin{array}{cc} a&b \\ c&d \end{array} \right\vert = ad-bc . \]
If the matrix entries are real numbers, the matrix A can be used to represent two linear maps: one that maps the standard basis vectors to the rows of A, and one that maps them to the columns of A. In either case, the images of the basis vectors form a parallelogram that represents the image of the unit square under the mapping. The parallelogram defined by the rows of the above matrix is the one with vertices at (0, 0), (a, b), (a + c, b + d), and (c, d), as shown in the accompanying diagram.

The formula for the determinant of a 3 × 3 matrix is

\[ \left\vert \begin{array}{cc} a&b&c \\ d&e&f \\ g&h&i \end{array} \right\vert = aei +bfg +cdh -ceg -bdi -afh . \]
As we see from the above formula, the determinant of 3×3 matrix A can be found by augmenting to A its first two columns and then summing the three products down the diagonal from upper left to lower right followed by subtracting the three products up the three diagonals from lower left to upper right. Unfortunately, this algorithm does not generalize to larger matrices.
A = {{a, b, c}, {d, e, f}, {g, h, i}}; Join[A, A[[All, 1 ;; 2]], 2] // MatrixForm
\( \begin{pmatrix} a&b&c&a&b \\ d&e&f&d&e \\ g&h&i&g&h \end{pmatrix} \)

In general, the determinant of an n × n matrix contains n! terms, half of them come up with positive sign and another half are negative.

A square matrix is called upper triangular (lower triangular) if all the entries below the main diagonal are zero (correspondingly, if all the entries above the main diagonal are zero). A square matrix is called triangular if it is either upper or lower triangular.

Properties of the determinant:

  1. det(In) = 1, where In in the n × n identity matrix.
  2. det(AT) = det(A), where AT denotes the transpose of A.
  3. If A is a square matrix with a zero row or column, then its determinant is zero.
  4. For square matrices A and B of equal size, det(AB) = det(A) det(B) = det(B) det(A).
  5. \[ \det \left( {\bf A}^{-1} \right) = \frac{1}{\det \left( {\bf A} \right)} . \]
  6. \( \det \left( k{\bf A} \right) = k^n \det \left( {\bf A} \right) \) for a constant k.
  7. If A is a triangular matrix, i.e. ai,j = 0 whenever i > j or, alternatively, whenever i < j, then its determinant equals the product of the diagonal entries.
  8. If B is a matrix resulting from an n × n matrix A by elementary row operation of swapping two rows, then det(B) = -det(A).
  9. If B is a matrix resulting from an n × n matrix A by elementary row operation of multiplying by a scalar k any row, then det(B) = k det(A).
  10. If B is a matrix resulting from an n × n matrix A by elementary row operation of multiplying by a scalar k any row and adding to another row, then det(B) = det(A).
1.   It is the definition of determinant.

2.   If A = [𝑎i,j], then \[ \det {\bf A} = \sum_{\sigma \in S_n} \mbox{sign}\left( \sigma \right) a_{1, \sigma (1)} a_{2, \sigma (2)} \ \cdots \ a_{n, \sigma (n)} . \] Since the ij-entry in transposed matrix AT is 𝑎j,i, we also have \[ \det {\bf A}^{\mathrm T} = \sum_{\rho \in S_n} \mbox{sign}\left( \rho \right) a_{\rho (1),1} a_{\rho (2), 2} \ \cdots \ a_{\rho (n),n} \] The sets of subscripts in the two sums are identical. The result follows.

3.  

4.   Let A = [𝑎i,j] and B = [bi,j] belong to 𝔽n×n. Let column j of A be 𝑎j and column j of B be bj. We have \[ {\bf A}\,{\bf B} = \left[ {\bf A}\,{\bf b}_1 \ {\bf A}\,{\bf b}_2 \ \cdots \ {\bf A}\,{\bf b}_n \right] . \] So for the determinant mapping δ, \[ \det \left( {\bf A}\,{\bf B} \right) = \delta \left( {\bf A}\,{\bf b}_1 ,\ {\bf A}\,{\bf b}_2 ,\ \cdots , \ {\bf A}\,{\bf b}_n \right) . \] Since \( \displaystyle {\bf A}\,{\bf b}_j = b_{1,j} {\bf a}_1 + b_{2,j} {\bf a}_2 + \cdots + b_{n,j} {\bf a}_n , \quad \) Theorem 1 implies \[ \det \left( {\bf A}\,{\bf B} \right) = \sum_{\sigma \in S_n} \mbox{sign}\left(\sigma \right) b_{1,\sigma (1)} b_{2,\sigma (2)} \cdots b_{n,\sigma (n)} \,\delta \left( {\bf a}_1 , \ldots , {\bf a}_n \right) = \left( \det{\bf B} \right) \left( \det {\bf A} \right) . \] The result follows the observation that (det B)(det A) = (det A)(det B).

5.   If A is invertible square matrix, then from \[ \det\left( {\bf A}^{-1} {\bf A} \right) = \det \left( {\bf I}_n \right) = 1, \] it follows that det(A−1A) = det(A−1) det(A), it follows that neither detA nor detA−1 is zero and that detA−1 = 1/detA.

6.  

7.   Let A = [𝑎i,j] be upper triangular square matrix, so that 𝑎i,j = 0 if i > j. Suppose ρ is different from ι in Sn. Let i in [1..n] be maximal so that ρ(i) ≠ i. If ρ(i) = j, then since ρ is a bijection, ρ(j) ≠ j, so i > j. It follows that \( \displaystyle a_{i,\rho (i)} = 0. \) From here we see that when ρ is in Sn, the only nonzero expression of the form \[ a_{1.\rho (1)} a_{2.\rho (2)} \cdots a_{n.\rho (n)} \] is the one for which ρ = ι. This proves the statement when A is upper triangular. We leave proof of the lower triangular case as an exercise.

8.  

9.  

10.  

Corollary 1: Similar matrices have the same determinant.

If we can transform a general square matrix A into a new triangular matrix T without changing the value (or as alternative, with simple and clear its modification), then we would have a method of computing its determinant. The way to change a general square matrix into an upper triangular matrix is through the three elementary row operations and their corresponding matrix multiplication counterparts. A matrix that is similar to a triangular matrix is referred to as triangularizable. Every matrix over the field of complex numbers ℂ is triangularizable, but not every real-valued matrix.

Example 1: Here's an example on how to compute the determinant of a 4x4 matrix, in general: \[ A = \begin{bmatrix} a&b&c&d \\ e&f&g&h \\ i&j&k&l \\ m&n&o&p \end{bmatrix} . \] Its determinant can be calculated as follows: \[ \det ({\bf A}) = a\cdot \det (F) - b \cdot \det (G) + c \cdot \det (H) - d\cdot \det (I) , \] where \[ F = \begin{bmatrix} f&g&h \\ j&k&l \\ n&o&p \end{bmatrix} , \quad G = \begin{bmatrix} e&g&h \\ i&k&l \\ m&o&p \end{bmatrix} , \quad H = \begin{bmatrix} e&f&h \\ i&j&l \\ m&n&p \end{bmatrix} , \quad I = \begin{bmatrix} e&f&g \\ i&j&k \\ m&n&o \end{bmatrix} . \]

Consider the matrix

\[ {\bf A} = \begin{bmatrix} 0&2&5&-1 \\ 3&2&-1&4 \\ 4&2&3&4 \\ 2&8&-1&4 \end{bmatrix} . \]
Its determinant contains 4! = 24 terms, each is a product of entries from A taken one from each row and each column; so using the Laplace expansion, we get
\[ \det{\bf A} = -2 \begin{vmatrix} 3&-1&4 \\ 4&3&4 \\ 2&-1&4 \end{vmatrix} + 5 \begin{vmatrix} 3&2&4 \\ 4&2&4 \\ 2&8&4 \end{vmatrix} + \begin{vmatrix} 3&2&-1 \\ 4&2&3 \\ 2&8&-1 \end{vmatrix} . \]
Next expansion gives We use Mathematica
A = {{0, 2, 5, -1}, {3, 2, -1, 4}, {4, 2, 3, 4}, {2, 8, -1, 4}}
Det[A]
2
Its inverse matrix is
Inv=Inverse[A] // TraditionalForm
\( \begin{pmatrix} -48&-89&57&20 \\ -8&-15&\frac{19}{2}&\frac{7}{2} \\ 12&22&-14&-5 \\ 43&80&-51&-18 \end{pmatrix} \)
The determinant of the inverse is
Det[Inv]
1/2
Now we swap two rows:
Am = {A[[1]], A[[4]], A[[3]], A[[2]]} Det[Am]
-2
We add two rows:
A[[1]] += A[[2]]
{3, 4, 4, 3}
A // TraditionalForm
\( \begin{pmatrix} 3&4&4&3 \\ 3&2&-1&4 \\ 4&2&3&4 \\ 2&8&-1&4 \end{pmatrix} \)
Det[A]
2
■
End of Example 1
Example 2: Let us consider two matrices
\[ {\bf A} = \begin{bmatrix} 0&2&5&-1 \\ 3&2&-1&4 \\ 4&2&3&4 \\ 2&8&-1&4 \end{bmatrix} \qquad \mbox{and} \qquad {\bf B} = \begin{bmatrix} 4&2&1&-1 \\ 3&2&-4&1 \\ 2&3&-1&5 \\ 2&-1&1&-6 \end{bmatrix} . \]
We calculate their products:
\[ {\bf A}\, {\bf B} = \begin{bmatrix} 14&20&-14&33 \\ 24&3&0&-30 \\ 36&17&-3&-11 \\ 38&13&-25&-23 \end{bmatrix} \qquad \mbox{and} \qquad {\bf B}\, {\bf A} = \begin{bmatrix} 8&6&22&4 \\ -8&10&0&-7 \\ 15&48&-1&26 \\ -11&-44&20&-26 \end{bmatrix} \]
A = {{0, 2, 5, -1}, {3, 2, -1, 4}, {4, 2, 3, 4}, {2, 8, -1, 4}}
B = {{4, 2, 1, -1}, {3, 2, -4, 1}, {2, 3, -1, 5}, {2, -1, 1, -6}}
A.B
{{14, 20, -14, 33}, {24, 3, 0, -30}, {36, 17, -3, -11}, {38, 13, -25, -23}}
B.A
{{8, 6, 22, 4}, {-8, 10, 0, -7}, {15, 48, -1, 26}, {-11, -44, 20, -26}}
Calculations show that
Det[A]
2
Det[B]
-3
Det[A.B]
-6
Det[B.A]
-6
So det(AB) = det(BA) = det(A) det(B) = det(B) det(A). However, if we swap two rows, its value will be
Aswaprows = {A[[3]], A[[2]], A[[1]], A[[4]]} ;
Det[Aswaprows]
-2
If we multiply one row, say 3, by a number, say 3, we get
Amultiply = {A[[1]], A[[2]], A[[3]], 3*A[[4]]} ;
Det[Amultiply]
6
If we add the second row to the third one, we obtain
Aadd = {A[[1]], A[[2]], A[[3]] + 3*A[[2]], A[[4]]} ;
Det[Aadd]
2
So this operation does not effect the value of the determinant. ■
End of Example 2
Example 3: Let us consider the 2×2 matrix
\[ {\bf A} = \begin{bmatrix} 0&1 \\ -1&0 \end{bmatrix} \]
that rotates the plane ℝ² down by angle π/2. WE introduce the complex-valued matrix
\[ {\bf S} = \begin{bmatrix} -{\bf j}&{\bf j} \\ 1&1 \end{bmatrix} \qquad \mbox{with} \qquad {\bf S}^{-1} = \frac{1}{2} \begin{bmatrix} {\bf j}&-{\bf j} \\ 1&1 \end{bmatrix} , \]
where j is the unit vector in positive vertical direction on the complex plane ℂ so j² = -1. Then
\[ {\bf S} \,{\bf A} \,{\bf S}^{-1} = \begin{bmatrix} -{\bf j}&0 \\ 0&{\bf j} \end{bmatrix} . \]
■
End of Example 3

 

Now it is time to make the process of converting a matrix to upper triangular a bit more automated using Mathematica. This can be done with two steps: first we use subroutine PivotDown that annihilates all entries in a column below a desired location. The second function, DetbyGauss uses PivotDown to convert a matrix to upper triangular, and when possible, do it without row exchange.
PivotDown[m_, {i_, j_}, oneflag_: 0] :=
Block[{k}, If[m[[i, j]] == 0, Return[m]];
Return[Table[
Which[k < i, m[[k]], k > i, m[[k]] - m[[k, j]]/m[[i, j]] m[[i]],
k == i && oneflag == 0, m[[k]] , k == 1 && oneflag == 1,
m[[k]]/m[[i, j]] ], {k, 1, Length[m]}]]]
DetbyGauss[mat_] := Block[ {row, column, matrix, m,n,k,t,swap},
row = 1; column =1; matrix = mat; swap = 0;
{m,n} = Dimensions[mat];
While[row < m && column < n,
Which[ matrix[[row, column]] != 0, matrix = PivotDown[matrix, {row, column}];
row ++; column ++;,
matrix[[row, column]] == 0, swap ++;
If[ Union[ Table[matrix[[k, column]], {k,row + 1, m}]] == {0}, swap --; column ++;,
t = row + Position[Map[#1 != 0 &, Table[matrix[[k, column]], {k, row +1, m}]], True][[1,1]];
matrix = Table[Which[k == row, matrix[[t]], k==t, matrix[[row]], True, matrix[[k]] ], {k,1,m}]] ]];
If[ swap >0, Print["there were ", swap, " row swap(s) "]];
Print[MatrixForm[matrix]];
Return[matrix]]
Example 4: Consider the previously use matrix
\[ {\bf A} = \begin{bmatrix} 0&2&5&-1 \\ 3&2&-1&4 \\ 4&2&3&4 \\ 2&8&-1&4 \end{bmatrix} . \]
Applying the subroutine DetbyGauss, we obtain its triangulation:
DetbyGauss[A]
there were 1 row swap(s)
\( \begin{pmatrix} 3&2&-1&4 \\ 0&2&5&-1 \\ 0&0&6&- \frac{5}{3} \\ 0&0&0&-\frac{1}{18} \end{pmatrix} \)
Multiplying the diagonal elements, we get the value of the determinant for the upper triangular matrix to be -2. However, since there was one swap, we have to multiply the latter by -1, which yields the correct answer: 2. ■
End of Example 4
Example 5: ■
End of Example 1

 

Example 6:
End of Example 6
  1. Convert the following matrices to upper triangular form and calculate the determinant. \[ \mbox{(a)} \quad \begin{bmatrix} 1&-1&1&-1 \\ -1&-1&-4&1 \\ 3&3&-1&1 \\ 8&-4&4&-5 \end{bmatrix} , \qquad \mbox{(b)} \quad \begin{bmatrix} 1&8&-3&8 \\ 6&1&-3&4 \\ 3&6&-1&5 \\ 7&-2&3&-4 \end{bmatrix} , \] \[ \mbox{(c)} \quad \begin{bmatrix} 3&5&-3&9&1 \\ -1&6&2&-3&4 \\ 3&4&6&-2&4 \\ 2&-2&5&3&-4 \\ 1&6&7&-1&2 \end{bmatrix} , \qquad \mbox{(d)} \quad \begin{bmatrix} 2&4&-2&1&1 \\ -1&5&1&-4&2 \\ 2&3&5&-1&3 \\ 1&-1&3&4&-2 \\ 1&6&7&-1&2 \end{bmatrix} \]

  1. Abeles, F.F., Chiò's and Dodgson's determinantal identities, Linear Algebra and its Applications, Volume 454, 1 August 2014, Pages 130-137.
  2. Axler, Sheldon, Down with determinants!, The American Mathematical Monthly, 1995, 102, No. 2, pp. 139--154.
  3. Axler, Sheldon, Linear Algebra Done Right (second edition), Springer, 1997.
  4. Muir, Thomas (1960) [1933], A treatise on the theory of determinants, Revised and enlarged by William H. Metzler, New York, NY: Dover
  5. Determinant Interactive Program and Tutorial by Kardi Teknomo.
  6. Determinants of order up to 6.
  7. Alsulaimani, Hamdan, Diagonal and triangular matrices, 2012.
  8. Salihu, A., Marevci, F., Chio’s-like method for calculating the rectangular (non-square) determinants: Computer algorithm interpretation and comparison, European journal of Pure and Applied Mathematics, Vol. 14, No. 2, 2021, pp. 431-450.