The Wolfram Mathematic notebook which contains the code that produces all the Mathematica output in this web page may be downloaded at this link. Caution: This notebook will evaluate, cell-by-cell, sequentially, from top to bottom. However, due to re-use of variable names in later evaluations, once subsequent code is evaluated prior code may not render properly. Returning to and re-evaluating the first Clear[ ] expression above the expression no longer working and evaluating from that point through to the expression solves this problem.

$Post := If[MatrixQ[#1], MatrixForm[#1], #1] & (* outputs matricies in MatrixForm*)
Remove[ "Global`*"] // Quiet (* remove all variables *)

Linear algebra is primarily concerned with two types of mathematical objects: vectors and their transformations or matrices. Moreover, these objects are common in all branches of science related to physics, engineering, and economics. Since matrices are build from vectors, this section focuses on the latter by presenting basic vector terminology and corresponding concepts. Fortunately, we have proper symbols for their computer manipulations.

There are two approaches in science literature to define vectors---one is abstract, especially those on linear algebra texts (you will meet it in part 3 of this tutorial), another trend involving engineering and physics topics is based on geometrical interpretation or coordinates definition, caring sequences of numbers. Computer science folks sit on both chairs because they utilize both interpretations of vectors. Moreover, they introduced abstract analogues of vectors---lists and arrays are widely used in mathematical books. We all observe a shift in science made by computer science including impact on classical mathematics.

Vectors

Mathematicians distinguish between vector and scalar (pronounced “SKAY-lur”) quantities. You’re already familiar with scalars—scalar is the technical term for an ordinary number. In this course, we use four specific sets of scalars: integers ℕ, rational numbers ℚ, real numbers ℝ, and complex numbers ℂ. We abbreviate these four sets with symbol &Fopf'. By a vector we mean a list or finite sequence of numbers. We employ scalars when we wish to emphasize that a particular quantity is not a vector quantity. For example, as we will discuss shortly, “velocity” and “displacement” are vector quantities, whereas “speed” and “distance” are scalar quantities.

In this section, we focus on algebraic definition of vectors as arrays of numbers and put its geometrical interpretation on back burner (Part 3).

   
Example 1: About 2,000 years ago, the ancient Greek engineer Philo of Byzantium came up with what may be the earliest design for a thermometer: a hollow sphere filled with air and water, connected by tube to an open-air pitcher. The idea was that air inside the sphere would expand or contract as it was heated or cooled, pushing or pulling water into the tube. In the second century A.D., the Greek-born Roman physician Galen created and may have used a thermometer-like device with a crude 9-degree scale, comprising four degrees of hot, four degrees of cold, and a “neutral” temperature in the middle.

It wasn’t until the early 1600s that thermometry began to come into its own. The famous Italian astronomer and physicist Galileo Galilei (1564--1642), or possibly his friend the physician Santorio, likely came up with an improved thermoscope around 1593: An inverted glass tube placed in a bowl full of water or wine. Santorio apparently used a device like this to test whether his patients had fevers. Shortly after the turn of the 17th century, English physician Robert Fludd also experimented with open-air wine thermometers.

The first recorded instance of anyone thinking to create a universal scale for thermoscopes was in the early 1700s. In fact, two people had this idea at about the same time. One was a Danish astronomer named Ole Christensen Rømer, who had the idea to select two reference points—the boiling point of water and the freezing point of a saltwater mixture, both of which were relatively easy to recreate in different labs—and then divide the space between those two points into 60 evenly spaced degrees. The other was England’s revolutionary physicist and mathematician Isaac Newton, who announced his own temperature scale, in which 0 was the freezing point of water and 12 was the temperature of a healthy human body, the same year that Rømer did. (Newton likely developed this admittedly limited scale to help himself determine the boiling points of metals, whose temperatures would be far higher than 12 degrees.)

After a visit to Rømer in Copenhagen, the Dutch-Polish physicist Daniel Fahrenheit (1686--1736) was apparently inspired to create his own scale, which he unveiled in 1724. His scale was more fine-grained than Rømer’s, with about four times the number of degrees between water’s boiling and freezing points. Fahrenheit is also credited as the first to use mercury inside his thermometers instead of wine or water. Though we are now fully aware of its toxic properties, mercury is an excellent liquid for indicating changes in temperature.

Originally, Fahrenheit set 0 degrees as the freezing point of a solution of salt water and 96 as the temperature of the human body. But the fixed points were changed so that they would be easier to recreate in different laboratories, with the freezing point of water set at 32 degrees and its boiling point becoming 212 degrees at sea level and standard atmospheric pressure.

But this was far from the end of the development of important temperature scales. In the 1730s, two French scientists, Rene Antoine Ferchault de Réamur (1683--1757) and Joseph-Nicolas Delisle (1688--1768), each invented their own scales. Réamur’s set the freezing point of water at 0 degrees and the boiling point of water at 80 degrees, convenient for meteorological use, while Delisle chose to set his scale “backwards,” with water’s boiling point at 0 degrees and 150 degrees (added later by a colleague) as water’s freezing point.

A decade later, Swedish astronomer Anders Celsius (1701--1744) created in 1742 his eponymous scale, with water’s freezing and boiling points separated by 100 degrees—though, like Delisle, he also originally set them “backwards,” with the boiling point at 0 degrees and the ice point at 100. (The points were swapped after his death.) In 1745, Carolus Linnaeus (1707--1778) of Uppsala, Sweden, suggested that things would be simpler if we made the scale range from 0 (at the freezing point of water) to 100 (water’s boiling point), and called this scale the centigrade scale. (This scale was later abandoned in favor of the Celsius scale, which is technically different from centigrade in subtle ways that are not important here.) Notice that all of these scales are relative—they are based on the freezing point of water, which is an arbitrary (but highly practical) reference point. A temperature reading of x°C basically means “x degrees hotter than the temperature at which water freezes.”

Then, in the middle of the 19th century, British physicist William Lord Kelvin (1824--1907) also became interested in the idea of “infinite cold” and made attempts to calculate it. In 1848, he published a paper, On an Absolute Thermometric Scale, that stated that this absolute zero was, in fact, -273 degrees Celsius. (It is now set at -273.15 degrees Celsius.)

Loudness:

Loudness is usually measured in decibels (abbreviated dB). To be more precise, decibels are used to measure the ratio of two power lev- els. If we have two power levels P₁ and P₂, then the difference in decibels between the two power levels is \[ 10\,\log_{10} \left( \frac{P_2}{P_1 \right) \ \mbox{dB} . \] So, if P₂ is about twice the level of P₁, then the difference is about 3 dB. Notice that this is a relative system, providing a precise way to measure the relative strength of two power levels, but not a way to assign a number to one power level.    ■
End of Example 1

Vectors and Points

The dimension of a vector tells how many numbers the vector contains. Vectors may be of any positive dimension, including one. In fact, a scalar can be considered a one dimensional (1D for short) vector. When writing a vector, mathematicians list the numbers surrounded by square brackets or parentheses; there are two common representations of vectors either as columns or as rows---we use both of them. Entries in a vector are usually separated by commas or just spaces. In either case, a vector written horizontally is called a row vector. Vectors are also frequently written vertically---they are called column vectors.

When studying matrices, you will see that vectors can also be represented by diagonal matrices. However, we concentrate our attention on these three types of vector representations as points or n-tuples, row vectors, and column vectors. For example, the following tree vectors can be treated differently by distinct computer solvers:

\[ \left( 1, 2, 3 \right) , \quad \begin{bmatrix} 4&5&6 \end{bmatrix} = \begin{pmatrix} 4&5&6 \end{pmatrix} \quad \mbox{or}\quad \begin{bmatrix} 3.14\\ -2 \\ 2.7 \end{bmatrix} = \begin{pmatrix} 3.14\\ -2\\ 2.7 \end{pmatrix} . \]
Strictly speaking, n-tuples are not vectors but points because they are elements of the Cartesian product and as so there is not vector structure. Points cannot be added as pixels on your screen, but you can add (or attach) a vector to a point and obtain a new point. It will be shown shortly that the corresponding space of points can be equipped with addition and scalar multiplication that makes it a vector space. In many textbooks, n-tuples are identified with vectors keeping in mind corresponding isomorphism between points and vectors.

Actually, row and column vectors are stored in computer memory as 1 × n and n × 1 matrices, respectively. Therefore, we denote the set of all n row vectors as 𝔽1×n or 𝔽1,n and the set of all column vectors as 𝔽n×1 or 𝔽n,1.

\[ \mathbb{R}^{n\times 1} = \left\{ \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} : \ x_1, x_2 , \ldots , x_n \in \mathbb{F} \right\} . \]
Similarly, the set of all n-row vectors is denoted by 𝔽1×n:
\[ \mathbb{F}^{1\times n} = \left\{ \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix} : \ x_1, x_2 , \ldots , x_n \in \mathbb{F} \right\} . \]
All computer solvers distinguish rows from columns. Some of them treat n-tuples or points as n dimensional row vectors. However, Mathematica distinguish n-tuples from row vectors. Besides these notations, it is common in physics to utilize Dirac's bra-ket notation, which we use in later chapters (Part 3 and Part 5).

As you know, a point has a location but no real size or thickness. In order to identify position of a point, we need to establish a global frame relative to which we specify location of a point. However, an “absolute” position does not exist. Every attempt to describe a position requires that we describe it relative to something else. Any description of a position is meaningful only in the context of some (typically “larger”) reference frame. Theoretically, we could establish a reference frame encompassing everything in existence and select a point to be the “origin” of this space, thus defining the “absolute” coordinate space. Luckily for us, absolute positions in the universe aren’t important. Do you know your precise position in the universe right now?

The Cartesian product of two sets A and B, denoted A × B, is the set of all ordered pairs (a, b) where a is in A and b is in B. In terms of set-builder notation, that is A x B == the set {(a,b) with a an element of A and b an element of B}. The Cartesian product of two or more sets is the set of all ordered pairs/n-tuples of the sets.

The term “Cartesian” is just a fancy word for “rectangular.” If you have ever played chess, you have some exposure to two dimensional (2D) Cartesian coordinate spaces.

hor0 = Graphics[{Red, Thickness[0.016], Line[{{-3, 0}, {3, 0}}]}]; ver0 = Graphics[{Red, Thickness[0.016], Line[{{0, -2.5}, {0, 2.5}}]}]; verm1 = Graphics[{Blue, Thickness[0.01], Line[{{-3, -2.5}, {-3, 2.5}, {-2.5, 2.5}, {-2.5, -2.5}, {-2, -2.5}, {-2, 2.5}, {-1.5, 2.5}, {-1.5, -2.5}, {-1, -2.5}, {-1, 2.5}, {-0.5, 2.5}, {-0.5, -2.5}}]}]; verp1 = Graphics[{Blue, Thickness[0.01], Line[{{3, -2.5}, {3, 2.5}, {2.5, 2.5}, {2.5, -2.5}, {2, -2.5}, {2, 2.5}, {1.5, 2.5}, {1.5, -2.5}, {1, -2.5}, {1, 2.5}, {0.5, 2.5}, {0.5, -2.5}}]}]; horp1 = Graphics[{Blue, Thickness[0.01], Line[{{-3, 2.5}, {3, 2.5}, {3, 2}, {-3, 2}, {-3, 1.5}, {3, 1.5}, {3, 1}, {-3, 1}, {-3, 0.5}, {3, 0.5}}]}]; horm1 = Graphics[{Blue, Thickness[0.01], Line[{{-3, -2.5}, {3, -2.5}, {3, -2}, {-3, -2}, {-3, -1.5}, {3, \ -1.5}, {3, -1}, {-3, -1}, {-3, -0.5}, {3, -0.5}}]}]; Show[hor0, ver0, horp1, verm1, verp1, horm1]
Figure 1: Map of the hypothetical city of Cartesia

Let’s imagine a fictional city named Cartesia. When the Cartesia city planners were laying out the streets, they were very particular, as illustrated in the map of Cartesia in Figure 1. As you can see from the map, Center Avenue runs east-west through the middle of town. All other east-west avenues (parallel to Center Avenue) are named based on whether they are north or south of Center Avenue, and how far they are from Center Avenue. Examples of avenues that run east-west are North 3rd and South 15th Avenue.

The other streets in Cartesia run north. Division Street runs north-south through the middle of town. All other north-south streets (parallel to Division Street) are named based on whether they are east or west of Division Street, and how far they are from Division Street.

Of course, the map of Cartesia is an idealization of rectangular plane---there is no limit in space of the Cartesian space, and streets do not have width being drawn through any point.

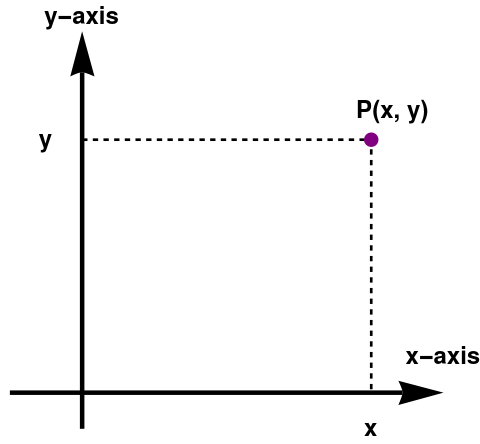
arx = Graphics[{Black, Thickness[0.01], Arrowheads[0.1], Arrow[{{-0.2, 0}, {1, 0}}]}]; ary = Graphics[{Black, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, -0.1}, {0, 1}}]}]; point = Graphics[{Purple, Disk[{0.8, 0.7}, 0.02]}]; txt = Graphics[{Black, Text[Style["P(x, y)", FontSize -> 18, Bold], {0.86, 0.78}], Text[Style["x-axis", FontSize -> 18, Bold], {1.0, 0.1}], Text[Style["x", FontSize -> 18, Bold], {0.8, -0.1}], Text[Style["y", FontSize -> 18, Bold], {-0.1, 0.7}], Text[Style["y-axis", FontSize -> 18, Bold], {0.0, 1.04}]}]; line = Graphics[{Black, Dashed, Thick, Line[{{0, 0.7}, {0.8, 0.7}, {0.8, 0}}]}]; Show[line, point, txt, arx, ary]
Figure 2: Location of a point

We consider points as elements of Cartesian product 𝔽n = 𝔽 × 𝔽 × ⋯ × 𝔽 of n scalar fields. Then every point P from ℝn has n coordinates that specify its position:

\begin{equation} \label{EqVector.1} P = \left( x_1 , x_2 , \ldots , x_n \right) \in \mathbb{R}^n = \mathbb{R} \times \mathbb{R} \times \cdots \times \mathbb{R} . \end{equation}

Since positions are relative to some larger frame, points are relative as well— they are relative to the origin of the coordinate system used to specify their coordinates. This leads us to the relationship between points and vectors. The following figure illustrates how the point (x, y) is related to the vector [x, y], given arbitrary values for x and y.

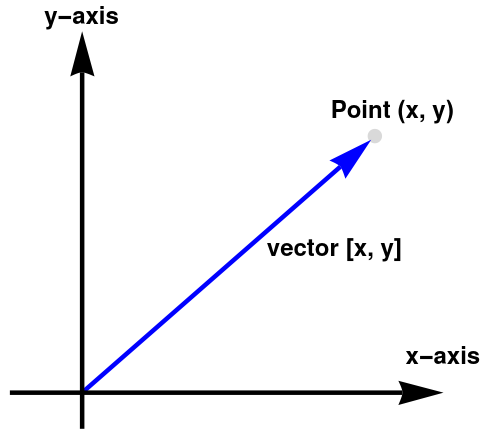
arx = Graphics[{Black, Thickness[0.01], Arrowheads[0.1], Arrow[{{-0.2, 0}, {1, 0}}]}]; ary = Graphics[{Black, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, -0.1}, {0, 1}}]}]; ar = Graphics[{Blue, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {0.8, 0.7}}]}]; point = Graphics[{LightGray, Disk[{0.81, 0.71}, 0.02]}]; txt = Graphics[{Black, Text[Style["Point (x, y)", FontSize -> 18, Bold], {0.86, 0.78}], Text[Style["x-axis", FontSize -> 18, Bold], {1.0, 0.1}], Text[Style["vector [x, y]", FontSize -> 18, Bold], {0.7, 0.4}], Text[Style["y-axis", FontSize -> 18, Bold], {0.0, 1.04}]}]; Show[point, ar, arx, ary, txt]
Figure 3: Point and vector

In many cases, displacements are from the origin, and so theew qill be no distinction between points and vectors because they both share the same coordinates. However, we often deal with quantities that are not relative to the origin, or any other point for that matter. In these cases, it is important to visualize these quantities as an arrow rather than a point.

The following construction shows how a Cartesian product 𝔽n of n scalar fields can betransfered into a vector space by introducing arithmetic operations inherited from scalar field.

A direct product of n fields is the Cartesian product of these fields, 𝔽n, equipped with two operations: addition \[ \left( x_1 , \ldots , x_n \right) + \left( y_1 , \ldots , y_n \right) = \left( x_1 + y_1 , \ldots , x_n + y_n \right) \] and scalar multiplication \[ \lambda \left( x_1 , \ldots , x_n \right) = \left( \lambda\,x_1 , \ldots , \lambda\, x_n \right) , \quad \lambda \in \mathbb{F} . \]

When we wish to refer to the individual components in a vector, we use subscript notation. In math literature, integer indices are used to access the elements. For example,

\[ {\bf a} = \begin{bmatrix} 1\\ 2 \\ 3 \end{bmatrix} = \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix} , \qquad \begin{split} a_1 &= a_x = 1, \\ a_2 &= a_y = 2, \\ a_3 &= a_z = 3 . \end{split} \]
As you see, we use lower case bold font to denote vectors. In opposite to vectors, we denote points by upper case letters in italic font. Since every multiple ℝ in ℝn is a real line containing all real numbers in natural order, every element of the Cartesian product is uniquely identified by a list of n numbers, which we call a point. Vectors are used to describe displacements, and therefore they can describe relative positions. Points are used to specify positions.

Every point on the plane has two coordinates P(x, y) relative to the origin of the coordinate system. This point can also be identified by a vector pointed to it and started from the origin. This means that the vector also can be uniquely identified by the same pair v = [x, y)]. This establishes a one-to-one correspondence between points and vectors.

Vector Properties

The term vector appears in a variety of mathematical and engineering contexts, which we will discuss in Part3 (Vector Spaces). There is no universal notation for vectors because of diversity of their applications. Until then, vector will mean an ordered set (list) of numbers. Generally speaking, concept of vector may include infinite sequence of numbers or other objects. However, in this part of tutorial, we consider only finite lists. There are many ways to represent vectors including columns, rows,

\begin{equation} \label{EqVector.2} {\bf v} = \left[ v_1 , v_2 , \ldots , v_n \right] \in \mathbb{R}^{1\times n} , \quad {\bf v}^{\mathrm T} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} \in \mathbb{R}^{n\times 1} . \end{equation}

For any given vector dimension, there is a special vector, known as the zero vector, that has zeroes in every position,

\[ {\bf 0} = \left[ 0, 0, \ldots , 0 \right] \quad\mbox{or} \quad {\bf 0} = \begin{bmatrix}0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} . \]
Note that zero vector is denoted by 0 in either case, independently whether it is a row vector or a column vector. Another importatnt case of vectors serve unit vectors:
\[ {\bf e}_1 = \left[ 1, 0, \cdots , 0 \right] , \ {\bf e}_2 = \left[ 0, 1, \cdots , 0 \right] , \ldots , \ {\bf e}_n = \left[ 0, 0, \cdots , 1 \right] . \]

These unit vectors can be written in column form

\[ {\bf e}_1 = \begin{bmatrix} 1\\ 0\\ \vdots \\ 0 \end{bmatrix} , \quad {\bf e}_2 = \begin{bmatrix} 0\\ 1\\ \vdots \\ 0 \end{bmatrix} , \quad \cdots , \quad {\bf e}_n = \begin{bmatrix} 0\\ 0\\ \vdots \\ 1 \end{bmatrix} . \]
In three dimensional case (3D) these vectors are usually denoted by
\[ {\bf i} = \begin{bmatrix} 1\\ 0 \\ 0 \end{bmatrix}^{\mathrm T} = \begin{bmatrix} 1& 0& 0 \end{bmatrix} , \quad {\bf j} = \begin{bmatrix} 0\\ 1 \\ 0 \end{bmatrix}^{\mathrm T} = \begin{bmatrix} 0& 1& 0 \end{bmatrix}, \quad {\bf k} = \begin{bmatrix} 0\\ 0 \\ 1 \end{bmatrix}^{\mathrm T} = \begin{bmatrix} 0& 0& 1 \end{bmatrix} , \]
where "T" stands for transposition. Note that in all other areas of mathematics, this operation is denoted by prime (') not by "T." With these unit vectors, every vector can be written as a linear combination of unit vectors (independently of their form, rows or columns):
\[ {\bf v} = x_1 {\bf e}_1 + x_2 {\bf e}_2 + \cdots + x_n {\bf e}_n , \]
for some scalars x₁, x₂, … , xn.

Another important operation is negation of a vector of any dimension (which is called "additive inverse"): we simply negate each component of the vector:
\[ - {\bf v} = (-1){\bf v} = - \left[ \begin{array}{c} v_1 \\ v_2 \\ \vdots \\ v_n \end{array} \right] = \left[ \begin{array}{c} - v_1 \\ -v_2 \\ \vdots \\ -v_n \end{array} \right] . \]
This is a particular case of vector multiplication by a scalar. Then adding a vector with its nerative always results the zero vector---this operation is called additive inverse.    
Example 2: Important properties of linear systems can be described with concept and notation of vectors. As a motivating example, let us consider a system of three equations \begin{align*} 2\,x_1 -3\,x_2 + x_3 &= 3, \\ -x_1 + 2\,x_2 - 4\,x_3 &= 5 , \\ 3\, x_1 + 4\,x_2 - 2\, x_3 &= 3. \end{align*} We rewrite this system in columns as \[ \begin{bmatrix} 2\,x_1 \\ - x_1 \\ 3\,x_1 \end{bmatrix} + \begin{bmatrix} -3\, x_2 \\ \phantom{-}2\, x_2 \\ \phantom{-}4\,x_2 \end{bmatrix} + \begin{bmatrix} \phantom{-1}x_3 \\ -4\, x_3 \\ -2\, x_3 \end{bmatrix} = \begin{bmatrix} 3 \\ 5 \\ 3 \end{bmatrix} \] because we know how to operate with numbers. So we assume that we can add these columns by adding corresponding components. Taking out common multiples in each column, we get \[ x_1 \begin{bmatrix} \phantom{-}2 \\ -1 \\ \phantom{-}3 \end{bmatrix} + x_2 \begin{bmatrix} -3 \\ \phantom{-}2 \\ \phantom{-}4 \end{bmatrix} + x_3 \begin{bmatrix} \phantom{-}1 \\ -4 \\ -2 \end{bmatrix} = \begin{bmatrix} 3 \\ 5 \\ 3 \end{bmatrix} . \] The expression in the left-hand side is known as a linear combination---it is obtained by adding two or more vectors that are multiplied by scalar values. Calling each column a vector, we denote them with lower case letter written in bold font:
\[ {\bf u}_1 = \begin{bmatrix} \phantom{-}2 \\ -1 \\ \phantom{-}3 \end{bmatrix} , \quad {\bf u}_2 = \begin{bmatrix} -3 \\ \phantom{-}2 \\ \phantom{-}4 \end{bmatrix} , \quad {\bf u}_3 = \begin{bmatrix} \phantom{-}1 \\ -4 \\ -2 \end{bmatrix} , \qquad {\bf b} = \begin{bmatrix} 3 \\ 5 \\ 3 \end{bmatrix} . \]
   ■
End of Example 2
   
Example 3: We demonstrate some operations with vectors from ℝ3×1, so our field of scalars is the set of real numbers ℝ. So adding two vectors, we have \[ \begin{bmatrix} \phantom{-}5 \\ -1 \\ \phantom{-}2 \end{bmatrix} + \begin{bmatrix} \phantom{-}2 \\ \phantom{-}5 \\ -7 \end{bmatrix} = \begin{bmatrix} \phantom{-}7 \\ \phantom{-}4 \\ -5 \end{bmatrix} = \begin{bmatrix} \phantom{-}2 \\ \phantom{-}5 \\ -7 \end{bmatrix} + \begin{bmatrix} \phantom{-}5 \\ -1 \\ \phantom{-}2 \end{bmatrix} . \]
{5, -1, 2} + {2, 5, -7}
{7, 4, -5}
So addition is commutative. If we add a vector with its negative (additive inverse), we get \[ \begin{bmatrix} \phantom{-}5 \\ -1 \\ \phantom{-}2 \end{bmatrix} + \begin{bmatrix} -5 \\ \phantom{-}1 \\ -2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} . \]
{5, -1, 2} + {-5, 1, -2}
{0, 0, 0}
Multiplying by a constant 3.1415926, we obtain \[ 3.1415926 \begin{bmatrix} \phantom{-}5 \\ -1 \\ \phantom{-}2 \end{bmatrix} = \begin{bmatrix} 15.7087963 \\ -3.1415926 \\ 6.2831852 \end{bmatrix} . \]
3.1415926 * {5, -1, 2}
{15.708, -3.14159, 6.28319}
   ■
End of Example 3

The entries of vectors are integers, but they are suitable only for class presentations by lazy instructors like me. In real life, the set of integers ℤ appears mostly in kindergarten. Therefore, vector entries could be any numbers, for instance, real numbers denoted by ℝ, or complex numbers ℂ. However, humans and computers operate only with rational numbers ℚ as approximations of fields ℝ or ℂ. Although the majority of our presentations involves integers for simplicity, the reader should understand that they can be replaced by arbitrary numbers from either ℝ or ℂ or ℚ. When it does not matter what set of numbers can be utilized, which usually the case, we denote them by 𝔽 and the reader could replace it with any field (either ℝ or ℂ or ℚ).

For our purposes, it is convenient to represent vectors as columns. This allows us to rewrite the given system of algebraic equations in compact form:
\[ x_1 {\bf u}_1 + x_2 {\bf u}_2 + x_3 {\bf u}_3 = {\bf b} . \]
In general, a system of m linear equations
\begin{align} a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n &= b_1 , \notag \\ a_{2,1} x_1 + a_{2,2} x_2 + \cdots + a_{2,n} x_n &= b_2 , \label{EqVector.3} \\ \ddots \qquad\qquad & \qquad \vdots \notag \\ a_{m,1} x_1 + a_{m,2} x_2 + \cdots + a_{m,n} x_n &= b_m , \notag \end{align}
with n unknowns, x1, x2, … , xn, can be similarly rewritten as a linear combination
\begin{equation} \label{EqVector.4} x_1 {\bf u}_1 + x_2 {\bf u}_2 + \cdots + x_n {\bf u}_n = {\bf b} . \end{equation}
of column vectors
\[ {\bf u}_1 = \begin{bmatrix} a_{1,1} \\ a_{2,1} \\ \vdots \\ a_{m,1} \end{bmatrix} , \quad {\bf u}_2 = \begin{bmatrix} a_{1,2} \\ a_{2,2} \\ \vdots \\ a_{m,2} \end{bmatrix} , \quad \cdots \quad {\bf u}_n = \begin{bmatrix} a_{1,n} \\ a_{2,2} \\ \vdots \\ a_{m,n} \end{bmatrix} , \qquad {\bf b} = \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{m} \end{bmatrix} . \]
The succinct form \eqref{EqVector.4} of the linear system of equations \eqref{EqVector.3} tells us that we can add vectors by adding their components
\[ {\bf u} + {\bf v} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} + \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} = \begin{bmatrix} u_1 + v_1 \\ u_2 + v_2 \\ \vdots \\ u_n + v_n \end{bmatrix} \]
and multiply by a number, say k as
\[ k\,{\bf u} = k \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} = \begin{bmatrix} k\,u_1 \\ k\,u_2 \\ \vdots \\ k\,u_n \end{bmatrix} . \]
The number k in ku is called a scalar: it is written in the lightface type to distinguish it from the boldface vector u. Note that components of vector u are also written in the lightface type because they are numbers that we call scalars. How to operate with numbers (scalars) everybody knows from school: they can be added/subtracted and multiplied/divided by nonzero number.

Remember that the form of vector representation as columns, rows, or n-tuples (parentheses and comma notation) depends on you. However, you must be consistent and use the same notation for addition or scalar multiplication. You cannot add a column vector and a row vector:

\[ \begin{bmatrix} 1 \\ 2 \end{bmatrix} + \left[ 1, \ 2 \right] \qquad{\bf wrong!} \]
because they have different structures. In physics, row vectors are usually called bra vectors and column vectors are named ket vectors. Also, you cannot manipulate row vectors and n-tuples:
\[ \left[ 1, \ 2,\ 3 \right] + \left( 1, \ 2,\ 3 \right) \qquad{\bf wrong!} \]
because (1, 2, 3) ∈ ℝ×ℝ×ℝ, but [1 2 3] is 1×3 matrix. Of course, all three sets ℝ×ℝ×ℝ, ℝ³, and ;ℝ₃ are equivalent since all are just descriptions (depending on humans) of the same vectors (nature).

Our definition of vectors as lists of numbers includes one very important ingredient---scalars. We primary use either the set of real numbers, denoted by ℝ or the set of complex numbers, denoted by ℂ. However, computers operate only with rational numbers, denoted by ℚ. Since elements from these sets of scalars can be added/subtracted and multiplied/divided (by non zero), they are called fields. Either of these fields is denoted by 𝔽 (meaning either ℝ or ℂ or ℚ).

---->

   Giusto Bellavitis  Michail Ostrogradsky      William Hamilton

The concept of vector, as we know it today, evolved gradually over a period of more than 200 years. The Italian mathematician, senator, and municipal councilor Giusto Bellavitis (1803--1880) abstracted the basic idea in 1835. The idea of an n-dimensional Euclidean space for n > 3 appeared in a work on the divergence theorem by the Russian mathematician Michail Ostrogradsky (1801--1862) in 1836, in the geometrical tracts of Hermann Grassmann (1809--1877) in the early 1840s, and in a brief paper of Arthur Cayley (1821--1895) in 1846. Unfortunately, the first two authors were virtually ignored in their lifetimes. In particular, the work of Grassmann was quite philosophical and extremely difficult to read. The term vector was introduced by the Irish mathematician, astronomer, and mathematical physicist William Rowan Hamilton (1805--1865) as part of a quaternion.

Vectors can be described also algebraically. Historically, the first vectors were Euclidean vectors that can be expanded through standard basic vectors that are used as coordinates. Then any vector can be uniquely represented by a sequence of scalars called coordinates or components. The set of such ordered n-tuples is denoted by \( \mathbb{R}^n . \) When scalars are complex numbers, the set of ordered n-tuples of complex numbers is denoted by \( \mathbb{C}^n . \) Motivated by these two approaches, we present the general definition of vectors.

Example 4: For given vectors u = (−2, 1) and v = (1, 2), find 3u + (−2)v.

Rewriting vectors u and v in column form, we have

\[ 3{\bf u} + (-2){\bf v} = 3 \begin{bmatrix} -2 \\ \phantom{-}1 \end{bmatrix} + (-2) \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} -6 - 2 \\ 3 -4 \end{bmatrix} = \begin{bmatrix} -8 \\ -1 \end{bmatrix} . \]
   ■
End of Example 4
Example 5: For given two vectors
\[ {\bf u} = \begin{bmatrix} \phantom{-}1 \\ -2 \\ \phantom{-}3 \end{bmatrix} \qquad \mbox{and} \qquad {\bf v} = \begin{bmatrix} \phantom{-}3 \\ -4 \\ \phantom{-}2 \end{bmatrix} , \]
represent vector
\[ {\bf b} = \begin{bmatrix} -5 \\ \phantom{-}6 \\ -1 \end{bmatrix} \]
as a linear combination of vectors u and v. So we need to find x₁ and x₂ such that
\[ x_1 {\bf u} + x_2 {\bf v} = {\bf b} = \begin{bmatrix} -5 \\ \phantom{-}6 \\ -1 \end{bmatrix} . \tag{2.1} \]
The definition of scalar multiplication and vector addition lead to
\[ x_1 \begin{bmatrix} \phantom{-}1 \\ -2 \\ \phantom{-}3 \end{bmatrix} + x_2 \begin{bmatrix} \phantom{-}3 \\ -4 \\ \phantom{-}2 \end{bmatrix} = \begin{bmatrix} -5 \\ \phantom{-}6 \\ -1 \end{bmatrix} , \]
which is the same as
\[ \begin{bmatrix} x_1 + 3 x_2 \\ -2 x_1 - 4 x_2 \\ 3 x_1 + 2 x_2 \end{bmatrix} =\begin{bmatrix} -5 \\ \phantom{-}6 \\ -1 \end{bmatrix} . \tag{2.2} \]
The vectors on the right and left sides of (2.2) are equal if and only if their corresponding entries are both equal. That is, x₁ and x₂ make the vector equation (2.1) true if and only if x₁ and x₂ satisfy the system
\[ \begin{split} x_1 + 3 x_2 &= -5 , \\ -2 x_1 -4 x_2 &= 6 , \\ 3x_1 + 2 x_2 &= 2 . \end{split} \tag{2.3} \]
To solve this system of equation, we apply row reduction to the augmented matrix
\[ \begin{bmatrix} \phantom{-}1 & \phantom{-}3 & -5 \\ -2 & -4 & \phantom{-}6 \\ \phantom{-}3 & \phantom{-}2 & -1 \end{bmatrix} \ \sim \ \begin{bmatrix} 1 & \phantom{-}3 & -5 \\ 0 & \phantom{-}2 & -4 \\ 0 & -7 & 14 \end{bmatrix} \ \sim \ \begin{bmatrix} 1 & 3 & -5 \\ 0 & 2 & -4 \\ 0 & 0 & \phantom{-}0 \end{bmatrix} \]
The solution of (2.3) is x₁ = 1 and x₂ = −2. Hence b is a linear combination of u and v with weights x₁ = 1 and x₂ = −2. That is,
\[ (1) \begin{bmatrix} \phantom{-}1 \\ -2 \\ \phantom{-}3 \end{bmatrix} + (-2) \begin{bmatrix} \phantom{-}3 \\ -4 \\ \phantom{-}2 \end{bmatrix} = \begin{bmatrix} -5 \\ \phantom{-}6 \\ -1 \end{bmatrix} . \]
   ■
End of Example 5

  1. Compute u −v and 3u −2v ---> \[ {\bf u} = \begin{bmatrix} -2 \\ \phantom{-}1 \end{bmatrix} , \quad {\bf v} = \begin{bmatrix} 3 \\ 2 \end{bmatrix} \qquad\mbox{and} \qquad {\bf u} = \begin{bmatrix} \phantom{-}1 \\ -1 \end{bmatrix} , \quad {\bf v} = \begin{bmatrix} \phantom{-}4 \\ -3 \end{bmatrix} . \]
  2. Write system of equations that is equivalent to the given vector equation.
    1. \[ x_1 \begin{bmatrix} \phantom{-}3 \\ -4 \end{bmatrix} + x_2 \begin{bmatrix} -1 \\ -2 \end{bmatrix} + x_3 \begin{bmatrix} \phantom{-}5 \\ -2 \end{bmatrix} = \begin{bmatrix} \phantom{-}1 \\ -1 \end{bmatrix}; \]
    2. \[ x_1 \begin{bmatrix} 3 \\ 0 \\ 2 \end{bmatrix} + x_2 \begin{bmatrix} -1 \\ \phantom{-}3 \\ \phantom{-}5 \end{bmatrix} + x_3 \begin{bmatrix} -2 \\ \phantom{-}7 \\ \phantom{-}2 \end{bmatrix} = \begin{bmatrix} 5 \\ 1 \\ 3 \end{bmatrix}; \]
    3. \[ x_1 \begin{bmatrix} 2 \\ 1 \\ 7 \end{bmatrix} + x_2 \begin{bmatrix} \phantom{-}3 \\ -2 \\ -5 \end{bmatrix} + x_3 \begin{bmatrix} \phantom{-}4 \\ -6 \\ \phantom{-}1 \end{bmatrix} = \begin{bmatrix} -5 \\ -4 \\ \phantom{-}2 \end{bmatrix} . \]
  3. Given \( \displaystyle {\bf u} = \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} , \ {\bf v} = \begin{bmatrix} \phantom{-}3 \\ -1 \\ -5 \end{bmatrix} , \quad\mbox{and} \quad {\bf b} = \begin{bmatrix} -5 \\ 5 \\ h \end{bmatrix} . \) For what value of h is b a linear combination of vectors u and v?
  4. Given \( \displaystyle {\bf u} = \begin{bmatrix} 4 \\ 3 \\ 1 \end{bmatrix} , \ {\bf v} = \begin{bmatrix} \phantom{-}2 \\ -2 \\ -3 \end{bmatrix} , \quad\mbox{and} \quad {\bf b} = \begin{bmatrix} 8 \\ h \\ 9 \end{bmatrix} . \) For what value of h is b a linear combination of vectors u and v?
  5. Rewrite the system of equations in a vector form
    \[ \begin{split} 2x_1 - 3 x_2 + 7 x_3 &= -1 , \\ -5 x_1 -2 x_2 - 3 x_3 &= 2 , \\ 3x_1 + 2 x_2 + 4 x_3 &= 3 . \end{split} \]
  6. Let \( \displaystyle {\bf u} = \begin{bmatrix} 3 \\ 1 \end{bmatrix} , \ {\bf v} = \begin{bmatrix} \phantom{-}2 \\ -2 \end{bmatrix} , \quad\mbox{and} \quad {\bf b} = \begin{bmatrix} h \\ k \end{bmatrix} . \) Show that the linear equation x₁u + x₂v = b has a solution for any values of h and k.
  7. Mark each statement True or False.
    1. Another notation for the vector (1, 2) is \( \displaystyle \begin{bmatrix} 1 \\ 2 \end{bmatrix} . \)
    2. An example of a linear combination of vectors u and v is 2v.
    3. Any list of of six complex numbers is a vector in ℂ6.
    4. The vector 2v results when a vector v + u is added to the vector v − u.
    5. The solution set of the linear system whose augmented matrix is [ a1 a2 a3 b ] is the same as the solution set of the vector equation x₁a₁ + x₂a₂ + x₃a₃ = b.
  1. Vector addition
  2. Tea
  3. Milk