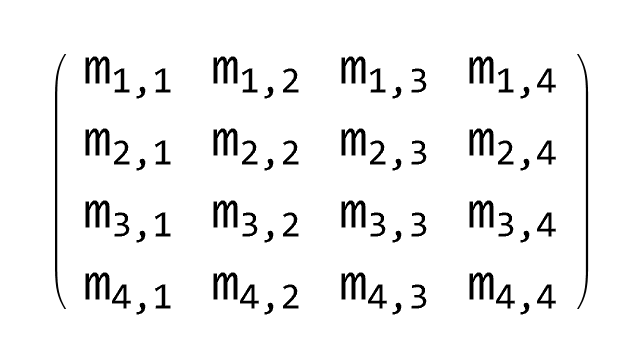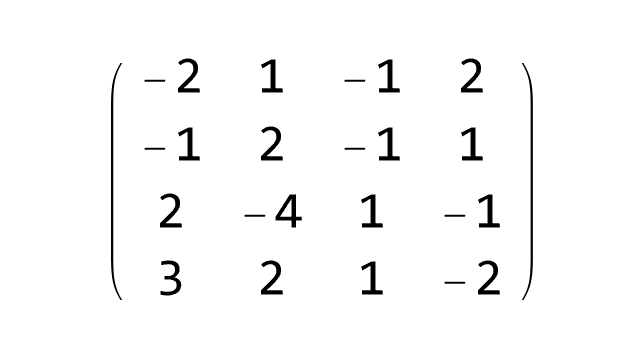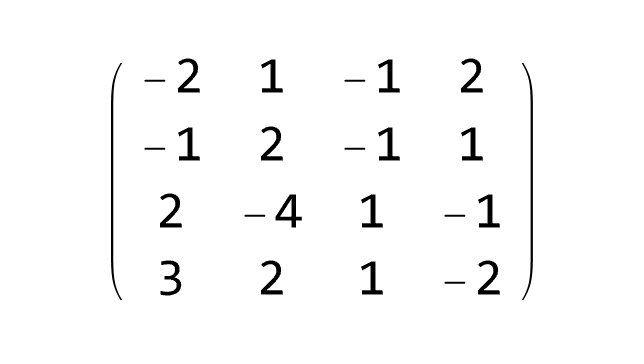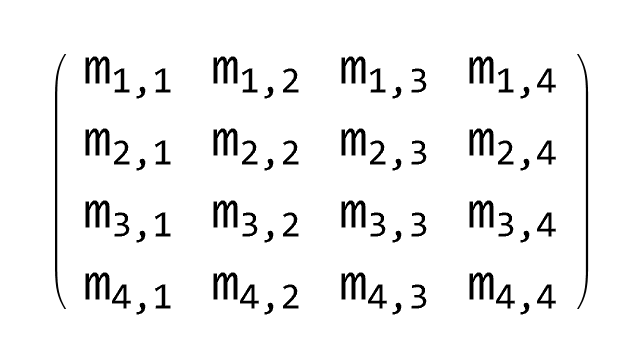Every m × n matrix A ∈ 𝔽^m×n with entries from field 𝔽 (which is either ℤ, set of integers, or ℚ, set of rational numbers, or ℝ, set of real numbers, or ℂ, set of complex numbers) generate a linear transformation T_A : 𝔽^n×1 ⇾ 𝔽^m×1 via matrix multiplication, 𝔽^n×1 ∋ x ↦ A x ∈ 𝔽^m×1.

Lemma 1: Let A be an m × n matrix and B be an n × k matrix, both over field 𝔽. Then if the injective map T_A(y) = A y that is also injective on the image (range) of B.

It is given that the product A B generates an injective map \[ T_{AB} \ : \ \mathbb{F}^{k\times 1} \,\mapsto \, \mathbb{F}^{m\times 1} , \quad \mbox{as} \quad T_{AB} \left( \mathbf{x}\right) = {\bf A}\,{\bf B}\,{\bf x} . \] The first multiple B must have zero null space. otherwise its product with A will be not injective. On image/range of B, transformation T_A must be injective to preserve one-to-one property. Therefore, it must be injective on the image of B. However, outside image(B) we have no information on mapping A.

Now we prove Lemma 1 analytically. Let x be any nonzero vector from 𝔽^n×1, then \begin{align*} {\bf A}\,{\bf B}\,{\bf x} \ne 0 \quad &\Longrightarrow \quad {\bf B}\,{\bf x} \ne 0 \qquad \forall \mathbf{x} \in \mathbb{F}^{k\timesd 1} \\ &\Longrightarrow \quad {\bf A}\,{\bf y} \ne 0 \qquad \mbox{where } \mathbf{y} = \mathbf{B}\,{\bf x} \quad \forall \ \mathbf{x} \in \mathbb{F}^{k \times 1} , \\ &\Longrightarrow \quad {\bf A}\,{\bf y} \ne 0 \qquad \mbox{for all {\bf y} in the image of {\bf B}}. \end{align*}

Example 1: We consider two matrices \[ \mathbf{A} = \begin{bmatrix} 1&0&0 \\ 0&1&1 \\ 0&0&0 \\ 0&0&0 \end{bmatrix} \qquad \mbox{and} \qquad \mathbf{B} = \begin{bmatrix} 1&0 \\ 0&1 \\ 0&0 \end{bmatrix} . \] We determine their null spaces with Mathematica:

A = {{1, 0, 0}, {0, 1, 1}, {0, 0, 0}, {0, 0, 0}};
B = {{1, 0}, {0, 1}, {0, 0}};
NullSpace[A]

NullSpace[B]

{}

So matrix B generates an injective (one-to-one) linear map T_B : ℝ^2×1 ⇾ ℝ^3×1. Its image (also known as range or column space) is a subspace of ℝ^3×1: \[ \mathbb{R}^{2\times 1} \ni {\bf v} = \left[ \begin{array}{c} x \\ y \end{array} \right] \, \mapsto \, \mathbf{B}\,{\bf v} = \left[ \begin{array}{c} x \\ y \\ 0 \end{array} \right] \in \mathbb{R}^{3\times 1} . \] Although the domain of matrix A is whole space ℝ^3×1, \[ \mathbb{R}^{3\times 1} \ni {\bf w} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right] \, \mapsto \, \mathbf{A}\,{\bf w} = \left[ \begin{array}{c} x \\ y \\ 0 \\ 0 \end{array} \right] \in \mathbb{R}^{4\times 1} , \] it operates on vectors from image B as one-to-one: \[ \mbox{image}(\mathbf{B}) \ni {\bf w} = \left[ \begin{array}{c} x \\ y \\ 0 \end{array} \right] \, \mapsto \, \mathbf{A}\,{\bf w} = \left[ \begin{array}{c} x \\ y \\ 0 \\ 0 \end{array} \right] \in \mathbb{R}^{4\times 1} . \] For their product, we have \[ {\bf A}\,{\bf B} = \begin{bmatrix} 1& 0 \\ 0& 1 \\ 0& 0 \\ 0& 0 \end{bmatrix} , \]

AB = A . B

{{1, 0}, {0, 1}, {0, 0}, {0, 0}}

NullSpace[AB]

{}

This example shows that the product of two matrices may have zero null space, but the forst matrix A is not injective. ■

End of Example 1

Lemma 2: Let A be an m × n matrix and B be an n × k matrix, both over field 𝔽. Then if the column space of their product A B spans 𝔽^m×1, then the column space of matrix B spans the whole space 𝔽^n×1.

In other words, if composition S ∘ T : 𝔽^k ⇾ 𝔽^m of two linear transformations is surjective (onto), then T : 𝔽^k ⇾ 𝔽ⁿ is also surjective.

Example 4: ■

End of Example 2

Matrix Rank

There are several equivalent definitions of matrix rank in the literature. We choose one of them and then prove its equivalence to other alternative definitions. It was invented in 1878 by the German mathematician Ferdinand Georg Frobenius (1849--1917). The work of Frobenius in 1878 was titled "On linear substitutions and bilinear forms". It was about the two important roles of matrices: to represent linear maps and bilinear forms despite the fact that the term matrix was not yet a part of Frobenius' mathematical vocabulary.

We assume that all matrix entries are from some field of scalars (either ℤ or ℚ or ℝ or ℂ). The space of all m-by-n matrices over field 𝔽 is denoted by 𝔽^m×n.

The rank of a matrix is determined by the highest order of a non-zero minor within it. Minor of the matrix is the determinant of the square sub-matrix that is obtained from the given matrix. If a matrix has a rank 'r', it means that at least one minor in the matrix is of order 'r', and any minors of order greater than 'r' are all zero.

Example 3:

MatrixRank[ m = {{1, 2, 0, -3, 1, 0}, {1, 2, 2, -3, 1, 2}, {1, 2, 1, -3, 1, 1}, {3, 6, 1, -9, 4, 3}}]

Then each of the following scripts determine a subset of linearly independent vectors:

m[[ Flatten[ Position[#, Except[0, _?NumericQ], 1, 1]& /@ Last @ QRDecomposition @ Transpose @ m ] ]]

Out[2]= {{1, 2, 0, -3, 1, 0}, {1, 2, 2, -3, 1, 2}, {3, 6, 1, -9, 4, 3}}

or, using subroutine

MinimalSublist[x_List] := Module[{tm, ntm, ytm, mm = x}, {tm = RowReduce[mm] // Transpose, ntm = MapIndexed[{#1, #2, Total[#1]} &, tm, {1}], ytm = Cases[ntm, {___, ___, d_ /; d == 1}]}; Cases[ytm, {b_, {a_}, c_} :> mm[[All, a]]] // Transpose]

we apply it to our set of vectors.

m1 = {{1, 2, 0, -3, 1, 0}, {1, 2, 1, -3, 1, 2}, {1, 2, 0, -3, 2, 1}, {3, 6, 1, -9, 4, 3}}; MinimalSublist[m1]

Out[3]= {{1, 0, 1}, {1, 1, 1}, {1, 0, 2}, {3, 1, 4}}

In m1 you see 1 row and n columns together,so you can transpose it to see it as column {{1, 1, 1, 3}, {0, 1, 0, 1}, {1, 1, 2, 4}} One can use also the standard Mathematica command: IndependenceTest. ■

End of Example 3

Rank is a property of the entire matrix and it is a nonnegative number, which we denote by rank(A). A rank of 0 is possible, but most matrices have a rank > 0. If fact, only the zeros matrix can have a rank = 0. The maximum possible rank of an m × n matrix is the smaller of m or n. That is,

\[ \mbox{rank}({\bf A}) \leqslant \min \left\{ m, \ n \right\} . \]

We will use the following terminology for full-rank matrices

If rank of m × n matrix A is m, then A is said to be full-row rank.
If rank of m × n matrix A is n, then A is said to be full-column rank.

Theorem 1: The rank of a matrix is the largest number of columns or rows that can form a linearly independent set.

Example 4: ■

End of Example 4

Theorem 2: Let M_r be a linear subspace of ℝ^n×n, the n²-dimensional vector space of squre matrices of size n with real entries, formed by matrices having a rank less than or equal to r, where 1 ≤ r < n. Then the dimension of i>M_r is less than or equal to 𝑛r.

We consider auxiliary subspace \[ E = \left\{ \begin{bmatrix} {\bf 0} & \mathbf{B} \\ \mathbf{B}^{\mathrm T} & \mathbf{A} \end{bmatrix} \ : \quad \mathbf{B} \in \mathbb{R}^{r \times (n-r)} , \quad \mathbf{A} \in \mathbb{R}^{(n-r) \times (n-r)} \right\} . \] Then \[ \mbox{dim}(E) = r \left( 𝑛−r\right) + (𝑛−r)^2 = \left( 𝑛−r\right)\left( r+𝑛−r\right) = 𝑛\left( 𝑛−r\right) . \] Let M_r be subspace of ℝ^n×n such that \[ M_r = \left\{ \mathbf{M} \in \mathbb{R}^{n \times n}\ : \quad \max \mbox{rank}\left( \mathbf{M} \right) = r\right\} . \] We can assume that this space contains the matrix \( \displaystyle \quad \mathbf{J} = \begin{bmatrix} \mathbf{I} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{bmatrix} \in \mathbb{R}^{n\times n} . \quad \) Indeed, this follows that every rectangular matrix is equivalent (upon application of row and column elementary operations) to such standard form matrix. This means that there dxist two invertible matrices P and Q such that J = P M Q. Correspondingly, we define a linear mapping φ : M_r → φ(M_r) defined by the formula: φ(M) = P M Q), which is a a rank-preserving bijective linear map for any invertible matrices P and Q.

If we take matrix M ∈ M_r ∩ E, then we can show, considering M + λJ \isin; M_r, that M = 0. Therefore, since \[ \dim \left( M_r + E \right) = \dim \left( M_r \right) + \dim \left( E \right) \leqslant \dim \left( \mathbb{R}^{n\times n} \right) = n^2 . \] So we get \[ \dim \left( M_r \right) \leqslant n^2 - n \left( n-r \right) = n\,r . \]

Example 5: ■

End of Example 5

Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.

Introduction to Linear Algebra

Systems of Linear Equations

Matrix Algebra

Vector Spaces

Eigenvalues, Eigenvectors

Euclidean Spaces

Matrix Decompositions

Applications

Functions of Matrices

Miscellany

Preliminaries

Glossary

Reference

Matrix Rank