This section provides a connection between ancient comprehension of vectors as quantities having magnitude and direction and vectors as arrays of numbers, presented in Part1 of this tutorial. The classical (geometrical) model of vectors is assumed to provoke curiosity, incite mathematical intuition, and prepare the beginner for the rigorous formalisms that follow.

Motivation

Quantities that completely specified by single data, like length, density, or mass, are called scalars. In this tutorial, we consider only scalars that are elements of three fields: ℚ (rational numbers), ℝ (real numbers), or ℂ (complex numbers). Quantities that are not scalars, but that can be added and multiplied by scalas are referred to as vectors.

The concept of a vector in its earliest manifestation comes from physical considerations. In particular, there is evidence of velocity being thought as a vector---a quantity with direction and magnitude---in ancient Greek times. For instance, the treatise Mechanice by an unknown author in the fourth century B.C. is written: "When a body is moved in a certain ratio (i.e., has two linear movements in a constant fraction of one to another) the body must move in a straight line, and this straight line is the diagonal of the parallelogram formed from the straight lines which have the given ratio." Heron of Alexandria (first century A.D.) gave a proof of this result when the directions were perpendicular. He showed that if a point P moves with a constant velocity over a line PQ while at the same time the line PQ moves with constant velocity along the parallel lines PR and QS so that it always remains parallel to its original position, and that if the time P takes to reach Q is the same as the time PQ takes to reach RS, then in fact the point P moves along the diagonal PS.

This basic idea of adding two motions vectorially was generalized from velocities to physical forces in the sixteenth and seventeenth centuries. One example of this practice is found the Law of Motion in Isaac Newton's Principia, where he shows that "a body acted on by two forces simultaneously will describe the diagonal of a parallelogram in the same time as it would describe the sides by those forces separately."

Before invention of rectangular coordinates in 1637 by the French philosopher, scientist, and mathematician René Descartes (1596--1650) (Latinized name: Cartesius), geometrical prospective dominated (including name "vector"). Since 85% of information comes to humans through eyes, developing a geometric intuition cannot be ignored.

Physicists have found a very useful geometric interpretation of forces acting on a body. The motion in response to a force depends on the direction in which the force is applied and on the magnitude of the force---that is, on how hard the force is exerted. It is natural to represent a force by an arrow, pointing in the direction in which the force is acting, and with the length of the arrow representing the magnitude of the force. Such an arrow is a force vector. In short, a vector is a term that refers colloquially to some quantities that cannot be expressed by a single number, but can be fully characterized by its magnitude and direction.

It leads naturally to describe a vector as an arrow. However, this geometrical approach has a serious limitation of being applied to quantities in low dimensions (up to three). So we need an algebraic description rather than geometrical one because computers accept only the former.

In most physical situations involving vectors, only the magnitude and direction of the vector are significant; consequently, we regard vectors with the same length and direction as being equal (or equivalent) irrespective to their positions. When we think of vectors as arrows, they are not based at the origin necessarily; a vector is simply the direction and the magnitude, and it does not know where it starts. A vector whose point of application is not fixed but magnitude and direction is, is called free vector. Fixed or localised vector is whose point of application is fixed.

vec = Graphics[{Arrowheads[0.1], {Thick, Blue, Arrow[{{0, 0}, {2, 1}}]}}]; vec = Graphics[{Arrowheads[0.1], {Thick, Blue, Arrow[{{0, 0}, {2, 1}}]}}]; vec3 = Graphics[{Arrowheads[0.1], {Thick, Black, Arrow[{{0, -1}, {2, 0}}]}}]; Show[vec, vec2, vec3]

Same vector can become free or fixed depending on scenario. Like if a force F is applied on a table which has rotational and translational motion. If we are Interested in Translational motion then we consider force F as free vector because we can move it to the centre of mass of the table in solving the problem. While solving rotational motion of the table, the point of application of force F is fixed since torque has to be calculated.

In applications, people deal with a variety of quantities that are used to describe the physical world. Examples of such quantities include distance, displacement, speed, velocity, acceleration, force, mass, momentum, energy, work, power, etc. All these quantities can by divided into two categories -- vectors and scalars.

---> The Cartesian coordinate system provides a natural generalization of vectors to higher dimensions independently of their geometrical interpretation of having magnitude and direction.

Using a rectangular coordinate system in the plane, note that if we consider a force vector to start from the origin (0, 0), then the vector is completely determined by the coordinates of the point at the tip of the arrow. Hence, we can consider each ordered pair in ℝ×ℝ to represent a vector in the plane as well as a point in the plane. When we wish to regard an ordered pair as a vector, we will use square brackets, rather than parentheses, to indicate this. Also, we often will write vectors as columns of numbers rather than as rows, and brackets notation is traditional for columns. Thus, we speak of the point (2, 1) in ℝ×ℝ and of the vector [2, 1] in ℝ₂ or vector \( \displaystyle \begin{bmatrix} 2 \\ 1 \end{bmatrix} \) in ℝ². To represent the point (2, 1) in the plane, we make a dot at the appropriate place, whereas if we wish to represent the vector [2, 1], we draw an arrow emanating from the origin with its tip at the place where we would plot the point (2, 1). Mathematically, there is no distinction between (2, 1) and [2, 1]. The different notation merely indicate different views of the same member of ℝ².

It is a custom to visualize vectors with arrows (geometric object on the plane or 3D space). The tail of the arrow is called the initial point of the vector and the tip the terminal point. To emphasis this approach, an arrow is placed above the initial and terminal points, for example, the notation \( {\bf v} = \vec{AB} \) tells us that A is the starting point of the vector v and its terminal point is B. In this tutorial (as in most science papers and textbooks), we will denote vectors in boldface type applied to lower case letters such as v, u, or x.

Practical life requires quantitative description of physical phenomena. For instance, saying that today is cold and windy does not provide enough information what kind of dressing is needed. So you need units for temperature and starting point, which is usually referred to as the origin. The general approach was accomplished with

 

Choosing a Cartesian coordinate system for a one-dimensional space—that is, for a straight line—involves identification of a point O of the line (the origin), a unit of length, and an orientation for the line. An orientation chooses which of the two half-lines determined by O is the positive and which is negative; we then say that the line "is oriented" (or "points") from the negative half towards the positive half. Then each point P of the line can be specified by its distance from O, taken with a + or − sign depending on which half-line contains P. It is a custom to choose orientation from left to right following habits to write in all European languages.

A line with a chosen Cartesian system is called a number line, denoted by ℝ in mathematics. Every real number has a unique location on the line. Conversely, every point on the line can be interpreted as a number in an ordered continuum such as the real numbers.

Let us consider a couple of motivated examples.
Example 1: from Physics

Our next example is the set of real numbers ℝ that is a vector space over the set of scalars ℝ. Considering this set as a vector space, we denote it as ℝ¹. Similar conclusion is true for the field of rational numbers ℚ. Example 2: Null-space of the derivative operator

 

Although we claim to be 3-dimensional beings, much of our mathematical lives has been lived in the plane. Actual physical representations of planes are everywhere, from the screen of your laptop and sheet of paper on which these words are printed, to the board on which your teacher writes, to the floor beneath your feet. Mathematically, the plane consists of points that have no dimensions (but pixels on your screen have).

There has been something missing from our good times in the plane however, and what is missing is arithmetic. The notion of adding points may seem a bit odd because addition is for numbers, not points. However, addition is legitimate for vectors. Most likely, you are familiar with (free) vectors on the plane that can be moved without changing their direction and magnitude. It is a custom to identify vectors with arrows (geometric objects). The tail of the arrow is called the initial point of the vector and the tip the terminal point. To emphasis this approach, an arrow is placed above the initial and terminal points, for example, the notation \( {\bf v} = \vec{AB} \) tells us that A is the starting point of the vector v and its terminal point is B. In this tutorial (as in most science papers and textbooks), we will denote vectors in boldface type applied to lower case letters such as v, u, or x.

Any two vectors x and y can be added in "tail-to-head" manner; that is, either x or y may be applied to any point and then another vector is applied to the endpoint of the first. If this is done, the endpoint of the latter is the endpoint of their sum, which is denoted by x + y. Besides the operation of vector addition there is another natural operation that can be performed on vectors---multiplication by a scalar that are often taken to be real numbers. When a vector is multiplied by a real number k, its magnitude is multiplied by |k| and its direction remains the same when k is positive and the opposite direction when k is negative. Such vector is denoted by kx.

These two sets, points and vectors, can be only identified with each other when a Cartesian system of coordinated is imposed on the plane. This requires choosing the origin, two perpendicular lines with orientation, and units in order to convert these lines into axes. Upon coordinization of the plane, we can identify its points (denoted geometrically by dots) with ordered pairs of numbers, known as coordinates. This allows us to establish one-to-one correspondence between these three sets: vectors, points on the plane, and ordered pairs of real numbers, denoted by ℝ².

The invention of Cartesian coordinates in 1649 by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra.

With this correspondence, we can define addition between their elements of these three sets based on known rules for vectors:

Also, we can define multiplication by real numbers as

Vectors can be described also algebraically. Historically, the first vectors were Euclidean vectors that can be expanded through standard basic vectors that are used as coordinates. Then any vector can be uniquely represented by a sequence of scalars called coordinates or components. The set of such ordered n-tuples is denoted by 𝔽ⁿ, where set of scalars 𝔽 is usually one of the following three fields: either set of rational numbers ℚ or set of real numbers ℝ or set of complex numbers ℂ. Motivated by these two approaches, we present the general definition of vectors.

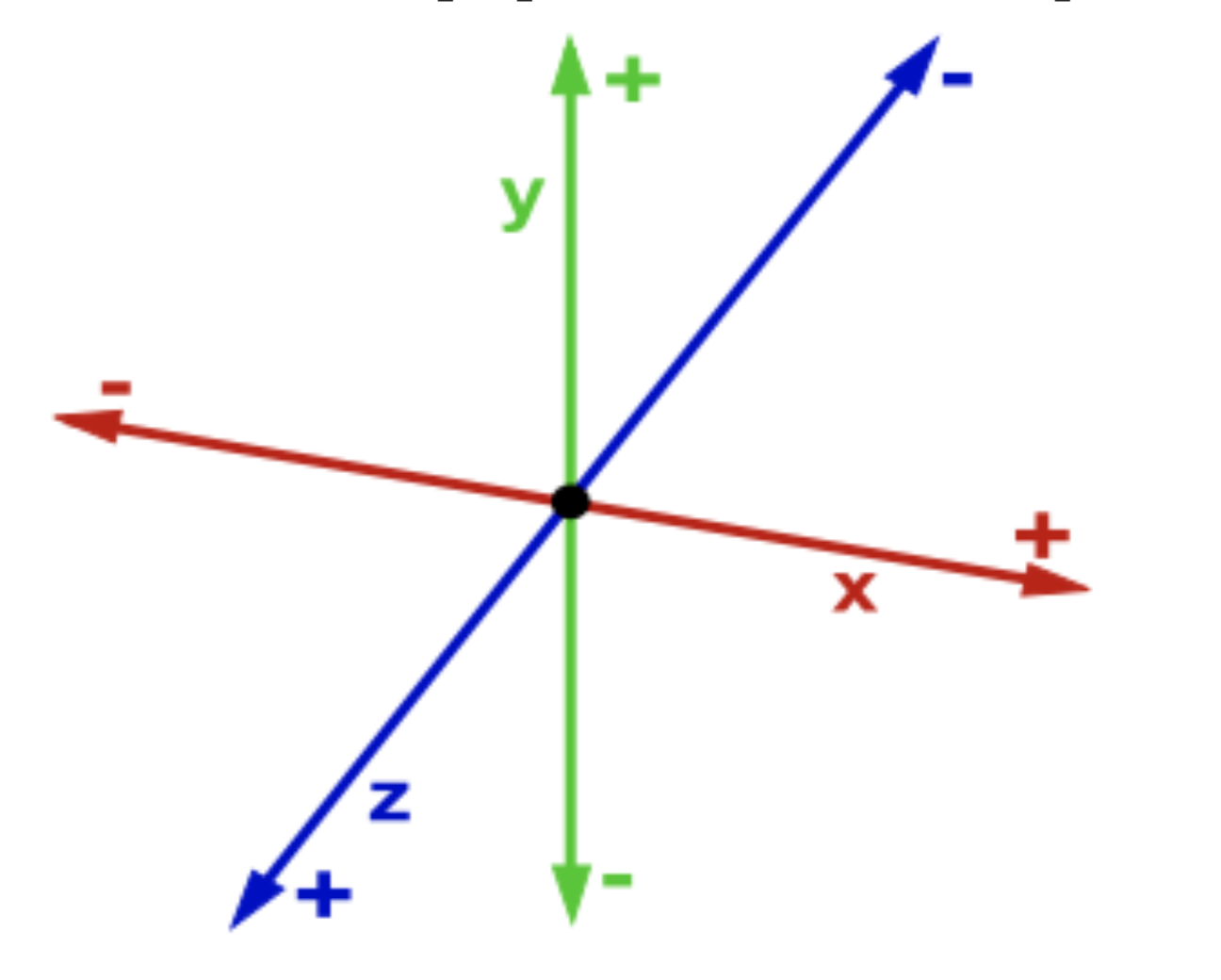
There are no universal names for the coordinates in the three axes. However, the horizontal axis is traditionally called abscissa borrowed from New Latin (short for linear abscissa, literally, "cut-off line"), and usually denoted by x. The next axis is called ordinate, which came from New Latin (linear), literally, line applied in an orderly manner; we will usually label it by y. The last axis is called applicate and usually denoted by z. Correspondingly, the unit vectors are denoted by i (abscissa), j (ordinate), and k (applicate), called the basis. Once rectangular coordinates are set up, any vector can be expanded through these unit vectors. In the three dimensional case, every vector can be expanded as \( {\bf v} = v_1 {\bf i} + v_2 {\bf j} + v_3 {\bf k} ,\) where \( v_1, v_2 , v_3 \) are called the coordinates of the vector v. Coordinates are always specified relative to an ordered basis. When a basis has been chosen, a vector can be expanded with respect to the basis vectors and it can be identified with an ordered n-tuple of n real (or complex) numbers or coordinates. The set of all real (or complex) ordered numbers is denoted by ℝⁿ (or ℂⁿ). In general, a vector in infinite dimensional space is identified by an infinite sequence of numbers. Finite dimensional coordinate vectors can be represented by either a column vector (which is usually the case) or a row vector. We will denote column-vectors by lower case letters in bold font, and row-vectors by lower case letters with a superimposed arrow. Because of the way the Wolfram Language uses lists to represent vectors, Mathematica does not distinguish column vectors from row vectors, unless the user specifies which one is defined. One can define vectors using Mathematica commands: List, Table, Array, or curly brackets.

In applications, people deal with a variety of quantities that are used to describe the physical world. Examples of such quantities include distance, displacement, speed, velocity, acceleration, force, mass, momentum, energy, work, power, etc. All these quantities can by divided into two categories -- vectors and scalars. A vector quantity is a quantity that is fully described by both magnitude and direction. On the other hand, a scalar quantity is a quantity that is fully described by its magnitude. In mathematics, physics, and engineering, a Euclidean vector (simply a vector) is a geometric object that has magnitude (or length) and direction. Many familiar physical notions, such as forces, velocities, and accelerations, involve both magnitude (the amount of the force, velocity, or acceleration) and a direction. In most physical situations involving vectors, only the magnitude and direction of the vector are significant; consequently, we regard vectors with the same length and direction as being equal irrespective to their positions.

Subsection: Exercises