Reflection

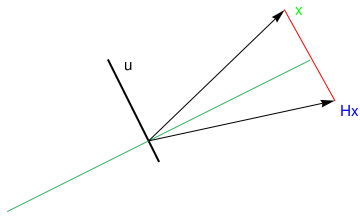
Suppose that we are given a line spanned over the vector a in ℝn and we need to find a matrix H of reflection about the line through the origin in the plane. This matrix H should fix every vector on line, and should send any vector not on the line to its mirror image about the line. The subspace { a }⊥ is called the hyperplane in ℝn orthogonal to a. The n × n orthogonal matrix
\[ {\bf H}_{\bf a} = {\bf I}_n - \frac{2}{{\bf a}^{\mathrm T} {\bf a}} \, {\bf a} \, {\bf a}^{\mathrm T} = {\bf I}_n - \frac{2}{\| {\bf a} \|^2} \, {\bf a} \, {\bf a}^{\mathrm T} \]
is called the Householder matrix or the Householder reflection about a, named in honor of the American mathematician Alston Householder (1904--1993). The complexity of the Householder algorithm is \( 2mn^2 - (2/3)\, n^3 \) flops (arithmetic operations). The Householder matrix \( {\bf H}_{\bf a} \) is symmetric, orthogonal, diagonalizable, and all its eigenvalues are 1's except one which is -1. Moreover, it is idempotent: \( {\bf H}_{\bf a}^2 = {\bf I} . \) When \( {\bf H}_{\bf a} \) is applied to a vector x, it reflects x through hyperplane \( \left\{ {\bf z} \, : \, {\bf a}^{\mathrm T} {\bf z} =0 \right\} . \)


P := {-3, -1}; Q := {3, 2};
lineseg = Graphics[{RGBColor[0.2, 0.7, 0.4], Line[{P, Q}]}]
u = Graphics[{Black, Thick, Line[{{0, 0}, {-1, 2}}]}]
ar1 := Graphics[Arrow[{{-0.2, 0.4}, {5/2, 3}}]]
ar2 := Graphics[Arrow[{{-0.2, 0.4}, {3.5, 1.2}}]]
line2 = Graphics[{RGBColor[1, 0, 0], Line[{{5/2, 3}, {3.5, 1.2}}]}]
textu = Graphics[Text[Style["u", FontSize -> 14, Black], {-0.6, 1.9}]]
textx = Graphics[Text[Style["x", FontSize -> 14, Red], {2.8, 3.0}]]
textHx = Graphics[Text[Style["Hx", FontSize -> 14, Blue], {3.8, 1.0}]]
Show[u, lineseg, ar1, ar2, line2, textu, textx, textHx]

Example 1: We present some simple reflections on the plane and in 3D in the following tables.

Operator
Illustration
Standard Matrix
Reflection about
the x-axis
T(x,y) = (x,-y)
\( \begin{bmatrix} 1&0 \\ 0&-1 \end{bmatrix} \)
Reflection about
the y-axis
T(x,y)=(-x,y)
\( \begin{bmatrix} -1&0 \\ 0&1 \end{bmatrix} \)
Reflection about
the line y=x
T(x,y)=(y,x)
\( \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix} \)
hor = Graphics[{Black, Thick, Arrow[{{-0.2, 0}, {1.6, 0}}]}]
ver = Graphics[{Black, Thick, Arrow[{{0, -0.2}, {0, 1.1}}]}]
ar1 = Graphics[{Blue, Thick, Arrow[{{0, 0}, {1, 1}}]}]
ar2 = Graphics[{Blue, Thick, Arrow[{{0, 0}, {1, -1}}]}]
dash = Graphics[{Dashed, Line[{{1, 1}, {1, -1}}]}]
textx = Graphics[Text[Style["(x,y)", FontSize -> 14], {1.1, 1.1}]]
textm = Graphics[Text[Style["(x,-y)", FontSize -> 14], {1.1, -1.1}]]
textu = Graphics[Text[Style["x", FontSize -> 14, Red], {1.58, 0.1}]]
textxx = Graphics[Text[Style["y", FontSize -> 14, Red], {0.1, 1.1}]]
Show[textx, textm, dash, ar1, ar2, ver, hor, textu, textxx]
hor = Graphics[{Black, Thick, Arrow[{{-1.2, 0}, {1.2, 0}}]}]
ver = Graphics[{Black, Thick, Arrow[{{0, -0.2}, {0, 1.2}}]}]
ar1 = Graphics[{Blue, Thick, Arrow[{{0, 0}, {1, 1}}]}]
ar2 = Graphics[{Blue, Thick, Arrow[{{0, 0}, {-1, 1}}]}]
dash = Graphics[{Dashed, Line[{{-1, 1}, {1, 1}}]}]
textx = Graphics[Text[Style["(x,y)", FontSize -> 14], {1.1, 1.1}]]
textm = Graphics[Text[Style["(-x,y)", FontSize -> 14], {-1.1, 1.1}]]
textu = Graphics[Text[Style["x", FontSize -> 14, Red], {1.28, 0.1}]]
textxx = Graphics[Text[Style["y", FontSize -> 14, Red], {0.1, 1.2}]]
Show[textx, textm, dash, ar1, ar2, ver, hor, textu, textxx]
hor = Graphics[{Black, Thick, Arrow[{{-0.2, 0}, {1.2, 0}}]}]
ver = Graphics[{Black, Thick, Arrow[{{0, -0.2}, {0, 1.2}}]}]
line = Graphics[{Blue, Thick, Line[{{0, 0}, {1, 1}}]}]
P= {Cos[0.4], Sin[0.4]}
Q = {Cos[0.4 + Pi/4], Sin[0.4 + Pi/4]}
ar1 = Graphics[{Blue, Thick, Arrow[{{0, 0}, P}]}]
ar2 = Graphics[{Blue, Thick, Arrow[{{0, 0}, Q}]}]
textyx = Graphics[Text[Style["y=x", FontSize -> 14], {0.86, 0.96}]]
textxx = Graphics[Text[Style["y", FontSize -> 14, Red], {0.1, 1.1}]]
textu = Graphics[Text[Style["x", FontSize -> 14, Red], {1.18, 0.1}]]
textx = Graphics[Text[Style["(y,x)", FontSize -> 14], {0.4, 1.0}]]
textm = Graphics[Text[Style["(x,y)", FontSize -> 14], {1.06, 0.4}]]
dash = Graphics[{Dashed, Line[{P, Q}]}]
Show[textx, textm, dash, ar1, ar2, ver, hor, line, textu, textxx, textyx]
Operator
Illustration
Standard Matrix
Reflection about
the xy-plane
T(x,y,z) = (x,y,-z)
\( \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&-1 \end{bmatrix} \)
Reflection about
the xz-plane
T(x,y,z)=(x,-y,z)
\( \begin{bmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{bmatrix} \)
Reflection about
the yz-plane
T(x,y,z)=(-x,y,z)
\( \begin{bmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \)
axes = Graphics3D[{Arrowheads[{{0.1, 1}}], Arrow[Tube[{{0, 0, 0}, {1.1, 0, 0}}, 0.02]], Arrow[Tube[{{0, 0, 0}, {0, 1.1, 0}}, 0.02]], Arrow[Tube[{{0, 0, 0}, {0, 0, 1.1}}, 0.02]]}, PlotRange -> {{-0.1, 1.6}, {-1, 1.1}, {-1.1, 1.1}}, Boxed -> False]
P = {1, 1, 1}
Q = {1, 1, -1}
ar1 = Graphics3D[{Blue, Thick, Arrow[{{0, 0, 0}, P}]}]
ar2 = Graphics3D[{Blue, Thick, Arrow[{{0, 0, 0}, Q}]}]
aa = ContourPlot3D[z == 0, {x, -0.1, 1}, {y, -0.1, 1}, {z, -1, 1}, AxesLabel -> {x, y, z}]
dash = Graphics3D[{Dashed, Line[{P, Q}]}]
textx = Graphics3D[ Text[Style["(x,y,z)", FontSize -> 14], {0.8, 1.0, 1.0}]]
textm = Graphics3D[ Text[Style["(x,y,-z)", FontSize -> 14], {1.06, 0.8, -1.0}]]
Show[textx, textm, dash, ar1, ar2, axes, aa]
End of Example 1

Example 2: Consider the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} . \) Then the Householder reflection with respect to vector u is

\[ {\bf H}_{\bf u} = {\bf I} - \frac{2}{9} \, {\bf u} \,{\bf u}^{\mathrm T} = \frac{1}{9} \begin{bmatrix} 7&4&-4 \\ 4&1&8 \\ -4&8&1 \end{bmatrix} . \]
The orthogonal symmetric matrix \( {\bf H}_{\bf u} \) is indeed a reflection because its eigenvalues are -1,1,1, and it is idempotent.
End of Example 2
■
Theorem 1: If u and v are distinct vectors in \( \mathbb{R}^n \) with the same norm, then the Householder reflection about the hyperplane \( \left( {\bf u} - {\bf v} \right)^{\perp} \) maps u into v and conversely. ■

We check this theorem for two-dimensional vectors \( {\bf u} = \left[ u_1 , u_2 \right]^{\mathrm T} \) and \( {\bf v} = \left[ v_1 , v_2 \right]^{\mathrm T} \) of the same norm. So given \( \| {\bf v} \| = \| {\bf u} \| , \) we calculate

\[ \| {\bf u} - {\bf v} \|^2 = \| {\bf u} \|^2 + \| {\bf v} \|^2 - \langle {\bf u}, {\bf v} \rangle - \langle {\bf v} , {\bf u} \rangle = 2 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) . \]
Then we apply the Householder reflection \( {\bf H}_{{\bf u} - {\bf v}} \) to the vector u:
\begin{align*} {\bf H}_{{\bf u} - {\bf v}} {\bf u} &= {\bf u} - \frac{2}{\| {\bf u} - {\bf v} \|^2} \begin{bmatrix} \left( u_1 - v_1 \right)^2 u_1 + \left( u_1 - v_1 \right) \left( u_2 - v_2 \right) u_2 \\ \left( u_1 - v_1 \right) \left( u_2 - v_2 \right) u_1 + \left( u_2 - v_2 \right)^2 u_2 \end{bmatrix} \\ &= \frac{1}{u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2} \begin{bmatrix} v_1 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) \\ v2 \left( u_1^2 + u_2^2 - u_1 v_1 - u_2 v_2 \right) \end{bmatrix} = {\bf v} . \end{align*}
Similarly, \( {\bf H}_{{\bf u} - {\bf v}} {\bf v} = {\bf u} . \) ■

Example 3:

Example. We find a Householder reflection that maps the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} \) into a vector v that has zeroes as its second and third components. Since this vecor has to be of the same norm, we get \( {\bf v} = \left[ 3, 0 , 0 \right]^{\mathrm T} . \) Since \( {\bf a} = {\bf u} - {\bf v} = \left[ -2, -2 , 2 \right]^{\mathrm T} , \) the Householder reflection \( {\bf H}_{{\bf a}} = \frac{1}{3} \begin{bmatrix} 1&-2&2 \\ -2&1&2 \\ 2&2&1 \end{bmatrix} \) maps the vector \( {\bf u} = \left[ 1, -2 , 2 \right]^{\mathrm T} \) into a vector v. Matrix \( {\bf H}_{{\bf a}} \) is idempotent (\( {\bf H}_{{\bf a}}^2 = {\bf I} \) ) because its eigenvalues are -1, 1, 1. ■ 

sage: nsp.is_finite()
False
End of Example 3
■

We use the Householder reflection to obtain an alternative version of LU-decomposition. Consider the following m-by-n matrix:

\[ {\bf A} = \begin{bmatrix} a & {\bf v}^{\mathrm T} \\ {\bf u} & {\bf E} \end{bmatrix} , \]
where u and v are m-1 and n-1 vectors, respectively. Let σ be the 2-norm of the first column of A. That is, let
\ [ \sigma = \sqrt{a^2 + {\bf u}^{\mathrm T} {\bf u}} . \]
Assume that σ is nonzero. Then the vector u in the matrix A can be annihilated using a Householder reflection given by
\[ {\bf P} = {\bf I} - \beta {\bf h}\, {\bf h}^{\mathrm T} , \]
where
\[ {\bf h} = \begin{bmatrix} 1 \\ {\bf z} \end{bmatrix} , \quad \beta = 1 + \frac{a}{\sigma_a} , \quad {\bf z} = \frac{\bf u}{\beta \sigma_a} , \quad \sigma_a = \mbox{sign}(a) \sigma . \]
It is helpful in what follows to define the vectors q and p as
\[ {\bf q} = {\bf E}^{\mathrm T} {\bf z} \qquad\mbox{and} \qquad {\bf p} = \beta \left( {\bf v} + {\bf q} \right) . \]
Then
\[ {\bf P}\,{\bf A} = \begin{bmatrix} \alpha & {\bf w}^{\mathrm T} \\ {\bf 0} & {\bf K} \end{bmatrix} , \]
where
\[ \alpha = - \sigma_a , \quad {\bf w}^{\mathrm T} = {\bf v}^{\mathrm T} - {\bf p}^{\mathrm T} , \quad {\bf K} = {\bf E} - {\bf z}\,{\bf p}^{\mathrm T} . \]

The above formulas suggest the following version of Householder transformations that access the entries of the matrix in a row by row manner.

Algorithm (Row-oriented vertion of Householder transformations):

Step 1: Compute \( \sigma_a \) and β

\[ \sigma = \sqrt{a^2 + {\bf u}^{\mathrm T} {\bf u}} , \qquad \sigma_a = \mbox{sign}(a) \,\sigma , \qquad \beta = a + \frac{a}{\sigma_a} . \]

Step 2: Compute the factor row \( \left( \alpha , {\bf w}^{\mathrm T} \right) : \)

\[ \alpha = - \sigma_a , \qquad {\bf z} = \frac{\bf u}{\beta \sigma_a} . \]
Compute the appropriate linear combination of the rows of A (except for the first column) by computing
\[ {\bf q}^{\mathrm T} = {\bf z}^{\mathrm T} {\bf E}, \qquad {\bf p}^{\mathrm T} = \beta \left( {\bf v}^{\mathrm T} + {\bf q}^{\mathrm T} \right) , \qquad {\bf w}^{\mathrm T} = {\bf v}^{\mathrm T} - {\bf p}^{\mathrm T} . \]

Step 3: Apply Gaussian elimination using the pivot row and column from step 2:

\[ \begin{bmatrix} 1 & {\bf p}^{\mathrm T} \\ {\bf z} & {\bf E} \end{bmatrix} \, \rightarrow \, \begin{bmatrix} 1 & {\bf p}^{\mathrm T} \\ {\bf 0} & {\bf K} \end{bmatrix} , \]
where \( {\bf K} = {\bf E} - {\bf z} \,{\bf p} ^{\mathrm T} . \) ■

This formulation of Householder transformations can be regarded as a special kind of Gauss elimination, where the pivot row is computed from a linear combination of the rows of the matrix, rather than being taken directly from it. The numerical stability of the process can be seen from the fact that \( |z_i | \le 1 \) and \( |w_j | \le \beta \le 2 \) for every entry in z and w.

The Householder algorithm is the most widely used algorithm for QR factorization (for instance, qr in MATLAB) because it is less sensitive to rounding error than Gram--Schmidt algorithm.

 

  1. Householder, Alston, S. Principles of Numerical Analysis, New York, McGraw Hill, 1953.