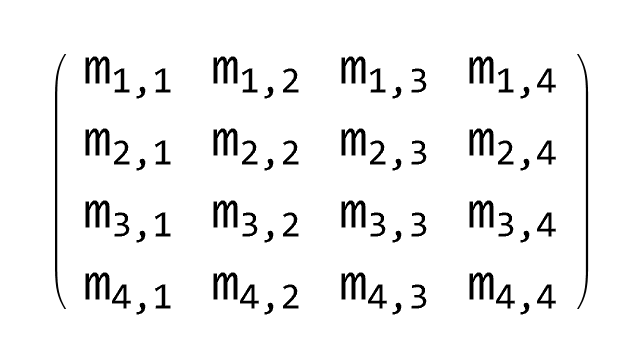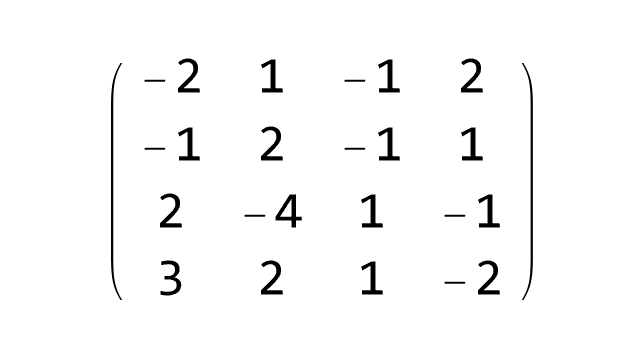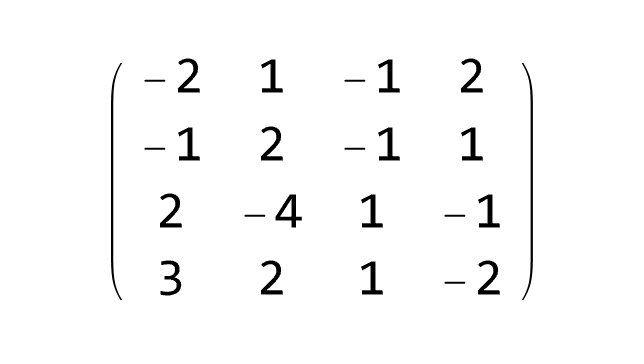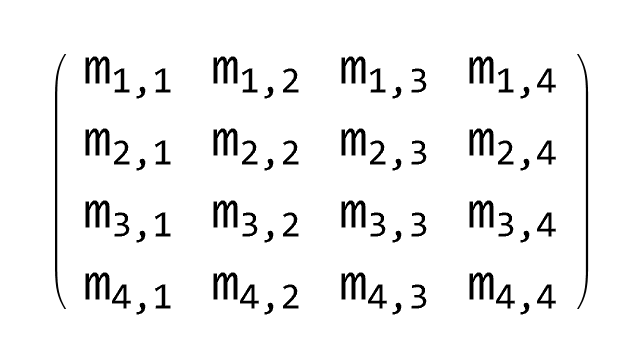es

Elementary Matrices

Inverse Matrices

Gaussian elimination

Column Transformations

Elementary matrices can be also used for column transformations when they are multiplied from right. We use Mathematica for their demonstrations. Let us first define an arbitrary 3 × 3 matrix:
\[ {\bf A} = \begin{bmatrix} a&b&c \\ d&e&f \\ g&h&i \end{bmatrix} . \]
A = {{a, b, c}, {d, e, f}, {g, h, i}}
We define an elementary matrix for switching first two columns:
\[ {\bf E}_1 = \begin{bmatrix} 0&1&0 \\ 1&0&0 \\ 0&0&1 \end{bmatrix} \qquad \Longrightarrow \qquad {\bf A}\, {\bf E}_1 = \begin{bmatrix} b&a&c \\ e&d&f \\ h&g&i \end{bmatrix} . \]
F1 = {{0, 1, 0}, {1, 0, 0}, {0, 0, 1}};
A . F
{{b, a, c}, {e, d, f}, {h, g, i}}
If we want to multiply the second column of an n × 3 matrix by 7, we would multiply from right the matrix by
\[ {\bf E}_2 (7) = \begin{bmatrix} 1&0&0 \\ 0&7&0 \\ 0&0&1 \end{bmatrix} , \]
which is the matrix that results when the second column of I₃ is multiplied by 7. We have
\[ {\bf A}\,{\bf E}_2 (7) = \begin{bmatrix} a&7\,b &c \\ d& 7\,e &f \\ g& 7\,h & i \end{bmatrix} . \]
F2 = {{1, 0, 0}, {0, 7, 0}, {0, 0, 1}};
A . F2
{{a, 7 b, c}, {d, 7 e, f}, {g, 7 h, i}}
Similarly, if we multiply from right by matrix
\[ {\bf F}_3 = \begin{bmatrix} 1 & 7 & 0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} , \]
we get
\[ {\bf A}\,{\bf E}_3 (7) = \begin{bmatrix} a& 7 a + b& c \\ d& 7 d + e& f \\ g& 7 g + h& i \end{bmatrix} . \]
F3 = {{1, 7, 0}, {0, 1, 0}, {0, 0, 1}};
A . F3
{{a, 7 a + b, c}, {d, 7 d + e, f}, {g, 7 g + h, i}}

 


  1. Axier, S., Linear Algebra Done Right. Undergraduate Texts in Mathematics (3rd ed.). Springer. 2015, ISBN 978-3-319-11079-0.
  2. Beezer, R.A., A First Course in Linear Algebra, 2017.
  4. Dillon, M., Linear Algebra, Vector Spaces, and Linear Transformations, American Mathematical Society, Providence, RI, 2023.