Preface
This tutorial was made solely for the purpose of education and it was designed for students taking Applied Math 0330. It is primarily for students who have very little experience or have never used Mathematica and programming before and would like to learn more of the basics for this computer algebra system. As a friendly reminder, don't forget to clear variables in use and/or the kernel. The Mathematica commands in this tutorial are all written in bold black font, while Mathematica output is in normal font.
Finally, you can copy and paste all commands into your Mathematica notebook, change the parameters, and run them because the tutorial is under the terms of the GNU General Public License (GPL). You, as the user, are free to use the scripts for your needs to learn the Mathematica program, and have the right to distribute this tutorial and refer to this tutorial as long as this tutorial is accredited appropriately. The tutorial accompanies the textbook Applied Differential Equations. The Primary Course by Vladimir Dobrushkin, CRC Press, 2015; http://www.crcpress.com/product/isbn/9781439851043
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part II of the course APMA0330
Glossary
Applications
Vertical Motion
It is known from elementary physics that, in the absence of air friction, a ball thrown up from the ground into earth's atmosphere with initial speed v0 would attain a maximum altitude of \( v_0^2 /(2g) .\) In this case the return time is \( 2\, v_0 /g, \) independent of the ball's mass. Here g is the acceleration due to gravity. If the ball is thrown up from altitude y0 (which we later assume to be zero), then the time T0 spent traveling is given by
The presence of air influences the ball's motion: it experiences two forces acting on it---the force of gravity and the air resistance force. Let's define the symbol T as follows:
Without air resistance, the object travels farther up than with air resistance. On the way down, without air resistance the object travels a larger distance, but it also gathers more speed. A natural question is, which travel time (with air resistance vs. no air resistance) is larger? Also, it is of interest to find the maximum altitude \( y_{\max} \) of the ball, the time Tmax to reach maximum altitude, and the time \( T_{\text{down}} \) to return back from ymax. Therefore, \( T_{\max} + T_{\text{down}} = T_{\text{total}} \) (the total time the ball spent in the air). The landing velocity is denoted by \( v_{\ell} . \)
Example: model for air resistance. Air resistance is the force that acts in the direction opposite to the motion of an object through air. Air resistance depends on the shape, material, and orientation of the object, the density of the air, and the object's relative speed.
We would like to think that there is a nice formula for the air resistance in terms of speed and other variables. Such a formula would help in making calculations and predicting various quantities. A starting point for obtaining such a formula is our everyday experience. Based on our experience, a reasonable assumption to make\footnote{Our intuition based on everyday experience is limited to a small range of conditions. This may lead to erroneous assumptions.
It has been observed that, under suitable conditions, the magnitude of the air resistance is proportional to a power of the speed s=|v|:
The air resistance force depends on the velocity (v) of the object at time t, so let us denote this force with the symbol F(v). Note that the air resistance, force F(v), always acts in the direction opposite to the motion. Therefore, F(v) acts in the down (negative) direction when the ball is moving up, and it acts in the up (positive) direction when the ball is moving down. If we measure the displacement y = y(t) vertically upwards from the ground, then \( v= {\text d}y/{\text d}t = \dot{y} \) is the velocity of the object. Newton's law of motion for the ball on the way up gives the differential equation
To find an equation for $v_{\ell}$, the landing velocity, we rewrite \refeq{vert.3} as \( {\text d}\,t = - {\text d}v/(g +F(v)/m) \) and integrate both sides from t=0 and v = v0 to \( t=T_{\max} \) and v=0. Here \( T_{\max} \) is the time to reach the maximum altitude \( y_{max} , \) which is also the time to have velocity v=0. We obtain,
To find an equation for $v_\ell$, we rewrite \refeq{vert.3} as \( v\,{\text d}t = -v\, {\text d}v/(g +F(v)/m) \) and integrate both sides from t=0 and v = v0 to \( t=T_{\max} \) and v=0. Here \( T_{\max} \) is the time to reach the maximum altitude \( y_{\max} , \) which is also the time to have velocity v=0. Using the fact that the integral of the velocity is the displacement, we obtain,
Solve[Integrate[v/(-g + 0.01*v^2), {v, 0, vl}] == Integrate[v/(g + 0.01*v^2), {v, 50, 0}], vl]
We would like to determine the ratio: \[ \gamma = T/T_0 = Tg/ \left( v_0 + \sqrt{v_0^2 +2 x_0 g}\right), \] where T time in air with air resistance and T0 is the time in air without air resistance.
For a tennis ball thrown upward with the initial velocity v0 =10, it is possible to find x0 that γ > 1 when p=0.9. In general, it is unknown for what values of p< 1, x0, and v0 we can achieve γ > 1.
Example: We consider a model of falling object, say a tennis ball, to a flat surface that moves up and down periodically. Using vertical axis directed upward, we denote v(t) as the velocity of the ball and y(t) as its position/height at time t. It has been observed that, under suitable conditions, the magnitude of the air resistance is proportional to the power of speeds=|v|:
Suppose that initially at t=0, the ball of mass m is dropped from the altitude \( y=h > 1 \) without initial velocity. At the same time, it is assumed that the floor starts moving according to the formula \( z= \sin \omega t. \) When elastic ball hits a hard flat surface, it bounces back with the same velocity. It is assumed that the collision is totally elastic, so the ball loses no kinetic energy in the collision, and its speed after collision is the same as before the collision. At this point, ignore the time needed for the ball to be deformed during collision before fully rebounded and has lifted off from the surface instantly. Hence the ball can be treated as a rigid body with negligible deformation during impact.
After collision, the ball climbs up until its velocity becomes zero, and then the ball falls vertically downward under the influence of gravity, hits the the moving floor, and bounces back.
Derivation of a differential equation
Newton's law of motion for the ball on the way down is
Input parameters
| \( g \approx 9.806 \) m/sec2 | the acceleration due to gravity near sea level at 45 deg. latitude; |
|---|---|
| m=0.08 | mass of the object, in kg because a tennis ball is about 80 grams; |
| k=0.02 | drag coefficient, positive; |
| p=2 | power of the speed term in the resistance force; |
| ω = π | frequency of the oscillating floor; |
| \( y_0 =h > 1 \) | initial altitude, positive, in meters. |
Derivation of solution
A ball that is dropped from height h> 1 can be described by its velocity v(t) and position y(t):
Integrate[A*Tanh[B*t], t]
k := 0.02; g := 9.806; m := 0.08; h0 := 2; (* h0 is the initial height *)
FindRoot[Sin[\[Pi] t] == h0 - 4*Log[Cosh[1.5657266683556232*t]], {t, 0.4}]
vv[t_] = omega*Cos[omega*t]
omega = Pi
y1[t_] = h0 - m/k*Log[Cosh[t*Sqrt[g*k/m]]]
kk=0.8
V1 = kk*vv[T1] + Sqrt[g*m/k]*Tanh[T1*Sqrt[g*k/m]]
On the second stage, the ball bounced up with the initial velocity \( V1 = kk*vv(T1) + \sqrt{\frac{gm}{k}} \tanh \left( \sqrt{\frac{gk}{m}}\,T1 \right) \approx 4.158 \) and from the position \( Y1 = \sin \left( \omega\,T1 \right) \approx 0.996038. \) Here kk is the coefficients of elastic damping of the racket, which we set to be 0.8. Therefore, we need to solve two initial value problems:
T2 = t /. FindRoot[v2[t] == 0, {t, 0.8}]
v3[t_] = -Sqrt[g*m/k]*Tanh[Sqrt[g*k/m]*(t - T2)]
Y2 = y2[T2]
T3 = t /. FindRoot[y3[t] == Sin[omega*t], {t, 2}]
0 < t < T1}, {Y1 + V1*(t - T1) + m/k*Log[Cos[Sqrt[g*k/m]*(T1 - t)]],
T1 < t <= T2}, {Y2 - 4*Log[Cosh[Sqrt[g*k/m]*(t - T2)]], T2 < t <= T3}}]
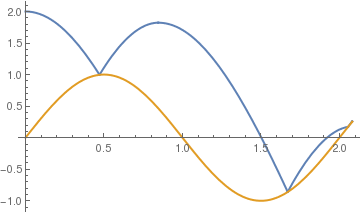
Plot[{y[t], Sin[omega*t]}, {t, 0, T3}]
y4[t_] = Y3 + V3*(t - T3) + m/k*Log[Cos[(T3 - t)*Sqrt[g*k/m]]]
T4 = t /. FindRoot[v4[t] == 0, {t, 2}]
yy4[t_] = YY4 + VV3*(t - TT4) + m/k*Log[Cos[(TT4 - t)*Sqrt[g*k/m]]]
y[t_] = Piecewise[{{h0 - m/k*Log[Cosh[t*Sqrt[g*k/m]]],
0 < t < T1}, {Y1 + V1*(t - T1) + m/k*Log[Cos[Sqrt[g*k/m]*(T1 - t)]],
T1 < t <= T2}, {Y2 - 4*Log[Cosh[Sqrt[g*k/m]*(t - T2)]],
T2 < t <= T3}, {Y3 + V3*(t - T3) +
m/k*Log[Cos[(T3 - t)*Sqrt[g*k/m]]], T3 < t < TT4}, {yy4[t], TT4 < t < 2.081}}]
Plot[{y[t], Sin[omega*t]}, {t, 0, 2.081}, PlotStyle -> {Thick, Thick}]
 |
 |
 |
|---|---|---|
| Claude Perrault | Sir Isaac Newton | Christiaan Huygens |
A tractrix (from the Latin verb trahere "pull, drag"; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a tractor (pulling) point that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Isaac Newton (1676) and Christiaan Huygens (1692).
Claude Perrault (1613 -- 1688) was a French architect, best known for his participation in the design of the east façade of the Louvre in Paris. He also achieved success as a physician and anatomist, and as an author, who wrote treatises on physics and natural history. Perrault was born and died in Paris. Aside from his influential architecture, he became well known for his translation of the ten books of Vitruvius, the only surviving Roman work on architecture, into French, written at the instigation of Colbert, and published, with Perrault's annotations, in 1673. His treatise on the five classical orders of architecture followed in 1683. As physician and natural philosopher with a medical degree from the University of Paris, Perrault became one of the first members of the French Academy of Sciences when it was founded in 1666.
Sir Isaac Newton (1642 -- 1726/27) was an English mathematician, astronomer, theologian and physicist (described in his own day as a "natural philosopher") who is widely recognized as one of the most influential scientists of all time and a key figure in the scientific revolution. His book Philosophiae Naturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy"), first published in 1687, laid the foundations of classical mechanics. Newton also made pathbreaking contributions to optics, and he shares credit with Gottfried Wilhelm Leibniz for developing the infinitesimal calculus.
Christiaan Huygens (Latin: Hugenius; 1629 -- 1695) was a prominent Dutch mathematician and scientist. He is known particularly as an astronomer, physicist, probabilist and horologist. Huygens was a leading scientist of his time. His work included early telescopic studies of the rings of Saturn and the discovery of its moon Titan, the invention of the pendulum clock and other investigations in timekeeping. He published major studies of mechanics and optics (having been one of the most influential proponents of the wave theory of light), and pioneered work on games of chance.
Example: In order to plot tractrix curve, use the following code:
Manipulate[
ParametricPlot[tractrix[a][t] // Evaluate, {t, 0, .99*\[Pi]},
PlotRange -> {0, 7}], {a, 1, 6}]
Plot[y'[x] = -Sqrt[a^2 - x^2]/x, {x, 0, 20},
PlotRange -> {-10, 10}], {a, 0, 20}]
Plot[-Sqrt[a^2 - x^2] + a Log[a] - a Log[a^2] - a Log[x] +
a Log[a^2 + a Sqrt[a^2 - x^2]], {x, 0, 20}, PlotRange -> All], {a,
1, 20}]
Example:: If a person becomes susceptible to a desease after recovering from it (like gonorrhea, meningitis, and streptococcal sore throat), then the percent of persons susceptible to becoming infected with the desease, S(t), and the percent of people in the population infected with the desease, I(t), can be modeled by the system of differential equations
Using the relation \( S+I =1 , \) we can eliminate one dependent variable and reduce the problem to an ordinary differential equation
toplot = Table[sol[[1, 1, 2]], {i0, 0.3, 1.1, 0.1}];
Plot[Evaluate[toplot], {t, 0, 6}, PlotStyle -> Thick]
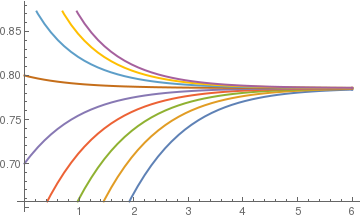
Module[{numsol},
numsol = NDSolve[{y'[t] == 1.1*y[t] - 1.4*(y[t])^2, y[0] == i0}, y[t], {t, 0, 10}];
Plot[y[t] /. numsol, {t, 0, 10}, DisplayFunction -> Identity]]
inits = Table[i, {i, 0.3, 1.1, 0.1}];
toshow = Map[graph, inits];
Show[toshow, DisplayFunction -> $DisplayFunction, PlotRange -> {0, 1}]
Example: : Forms of a given element with different numbers of protons, neutrons, and its nuclear energy are called nuclides. Some nuclides are not stable. For example, potassium-40 (40K) naturally very clowly decays to reach argon-40 (40Ar). This decay was first observed, but not understood, by the Nobel laureate Henri Becquerel (1852--1908) in 1896. However, Marie Skłodowska Curie (1867--1934) began studying this decay in 1898, cointed out it as radioactivity, and discovered the radioactive substances polonium and radium.
Given a sample of 40K of sufficient size, after \( 1.2 \times 10^{9} \) years approximately half of the sample will have decayed to 40Ar. The half-life of a nuclide is the time for half the nuclei in a given sample to decay.
Suppose you know that the half-life of polonium-209 is about 125 years. What percent of the original amount of 209Po remains after 75 years?
Let y0 represent te original amount of polonium-209 that is present and y(t) denote the amount of 209Po after t years. Then y(t) is the solution to the following initial value problem:
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value
Problems)