Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Return to Part I of the course APMA0330

Glossary

Preface

This section addresses a buitiful application of Mathematica to plot figures with fillings. Therefore, this section presents numerous examples.

Plotting with filling

      We repeat the previously considered example for a piecewise linear function with filling:
Plot[2 - 2*x, {x, 0, 1}, FillingStyle -> Green, Filling -> Bottom]
        Piecewise linear function            Mathematica code

      Now we change the color of filling:
Plot[2 - 2*x, {x, 0, 1}, FillingStyle -> Green, Filling -> Bottom]
        Example of green color filling.            Mathematica code

      Now we change the color of filling:
Plot[{2, (x/3)}, {x, 0, 6}, Filling -> {1 -> {2}}, FillingStyle -> LightCyan]
        Example of light cyan color filling.            Mathematica code

      This specifies a specific filling to be used only for the first curve.
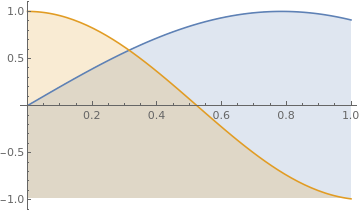
Plot[{Sin[2*x], Cos[3*x]}, {x,0,1}, Filling -> {1 -> 0.5}]
        Two curves with distinct fillings.            Mathematica code

     
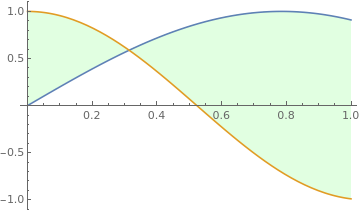
Plot[{Sin[2*x], Cos[3*x]}, {x, 0, 1}, Filling -> Bottom]
        Region between sine and cosine functions.            Mathematica code

      Another color of filling:
Plot[{Sin[2*x], Cos[3*x]}, {x, 0, 1}, Filling -> {1 -> {2}}, FillingStyle -> LightGreen]
        Region between sine and cosine functions.            Mathematica code

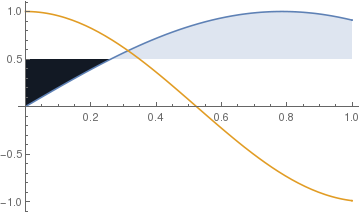
      This code specifies a specific filling to be used only for the first curve.
Plot[{Sin[2*x], Cos[3*x]}, {x,0,1}, Filling -> {1 -> 0.5}]
        Only one part of the region is specified.            Mathematica code

     
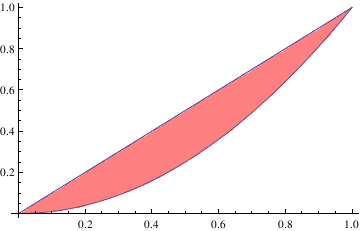
Plot[{x, x^2}, {x, 0, 1}, Filling -> {1 -> {2}}, FillingStyle -> Pink]
        Region between two curves.            Mathematica code

      Now we change the color of filling:
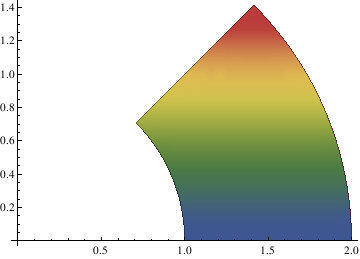
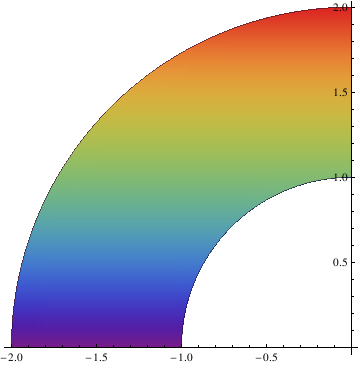
Show[PolarPlot[{1, 2}, {t, 0, Pi/4}], RegionPlot[ x^2 + y^2 >= 1 && x^2 + y^2 <= 4 && y/x <= 1, {x, 0, 2}, {y, 0, 2}, ColorFunction -> "DarkRainbow"]]
        Example of PolarPlot.            Mathematica code

     
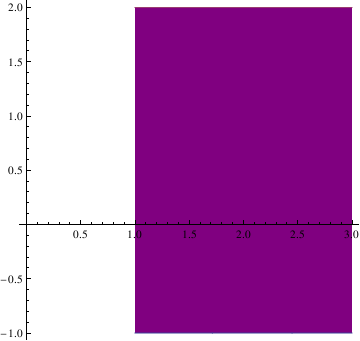
Plot[{-1, 2}, {x, 1, 3}, Filling -> {1 -> {2}}, FillingStyle -> Purple, AspectRatio -> Automatic, AxesOrigin -> {0, 0}]
        Rectangle.            Mathematica code

     
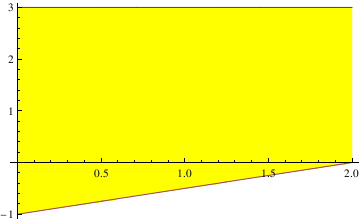
Plot[{3, (x/2) - 1}, {x, 0, 2}, Filling -> {1 -> {2}}, FillingStyle -> Yellow]
        Figure with filling.            Mathematica code

     
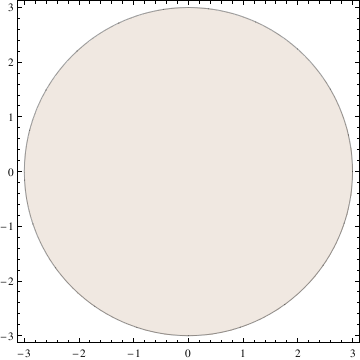
RegionPlot[{x^2 + y^2 <= 9}, {x, -3, 3}, {y, -3, 3}, PlotStyle -> LightBrown]
        Figure with filling.            Mathematica code

     
Show[PolarPlot[{1, 2}, {t, Pi/2, Pi}], RegionPlot[x^2 + y^2 >= 1 && x^2 + y^2 <= 4, {x, -2, 0}, {y, 0, 2}, ColorFunction -> "Rainbow"]]
        Part of a circle with filling.            Mathematica code

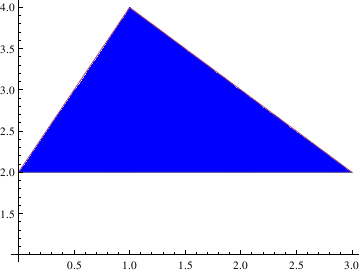
      To lift a traingle over the horizontal axis, type:
tr = Plot[{1., Max[1, Min[2 x + 1, 4 - x]]}, {x, 0, 3}, AspectRatio -> 1/2, Ticks -> {{0, 1, 2, 3}, {0, 1, 2, 3}},
Filling -> Axis, FillingStyle -> Blue, Axes -> True, AxesStyle -> Directive[Thick]]
a = Graphics[{{Opacity[0], White, tr[[1]]}, GeometricTransformation[{Opacity[1], Blue, tr[[1]]}, TranslationTransform[{0, 1}]]}]
Show[a, Axes -> True, AxesStyle -> Black, AspectRatio -> 0.75]
        Triangle is lifted over the axis.            Mathematica code

 

RegionPlot[Sin[x y] > 0, {x, -1, 1}, {y, -1, 1},
FrameTicksStyle -> Directive[FontOpacity -> 0, FontSize -> 0]]
When plotting, you still see frameticks data:
rp = RegionPlot[x^2 + y^3/4 < 2 && x + y < 1, {x, -2, 2}, {y, -2, 2}, FrameTicks -> Automatic]
First extract the frameticks information and change the labels to blank:
newticks = Last@First[AbsoluteOptions[rp, FrameTicks]];
While Mathematica complains about that Ticks: {Automatic,Automatic} is not a valid tick specification, it still does its job. next we type:
Show[rp, FrameTicks -> newticks]
You may also try
newticks = Last@First[AbsoluteOptions[rp, FrameTicks]];
newticks[[All, All, 2]] = "";
but Mathematica will complain again and out will be the same.

RegionPlot[1 < Abs[x + I y] < 2, {x, -2, 2}, {y, -2, 2}, ImagePadding -> 1]
      Another example:
Graphics3D[{Texture[img], EdgeForm[], Cylinder[{{0, 0, 0}, {0, 0, 2 Pi}}, 1]}, Boxed -> False]
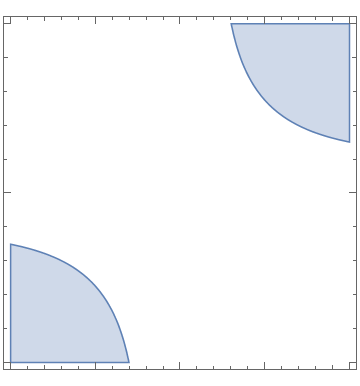
        Two pieces of a circle.            Mathematica code

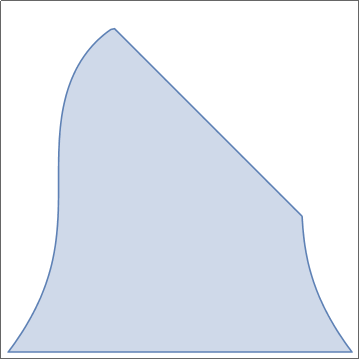
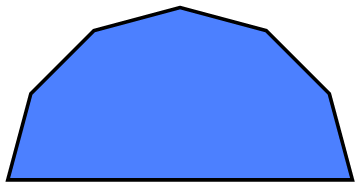
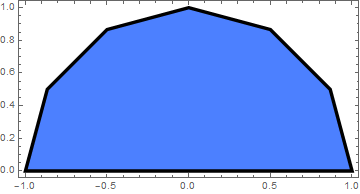
We plot half of the polygon:
poly = Polygon[Table[N[{Cos[n *Pi/6], Sin[n*Pi/6]}], {n, 0, 6}]]
Graphics[{RGBColor[0.3, 0.5, 1], EdgeForm[Thickness[0.01]], poly}]
Show[%, Frame -> True]

     
ill = Graphics[{LightRed, Polygon[Table[{0.99 Cos[theta], 0.99 Sin[theta]}, {theta, Pi + 0.3, 2 Pi - 0.25, 0.05}]]}];
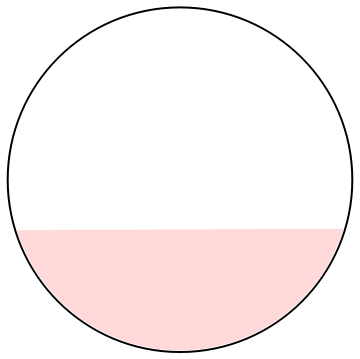
circle = Graphics[{Black, Thick, Circle[{0, 0}, 1.0]}];
Show[circle, fill]
        Circle with inclusion.            Mathematica code

 

Parametric Plots with fillings

     
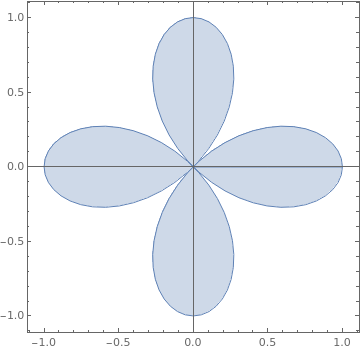ParametricPlot[ Cos[2 theta] {Cos[theta], Sin[theta]} r, {theta, 0, 2 Pi}, {r, 0, 1}, Mesh -> False, PlotPoints -> {30, 2}]
        Four cusp curve r = cos(2 θ).            Mathematica code

     
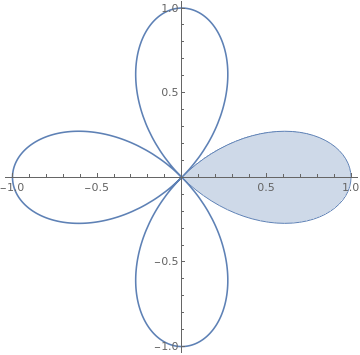g1 = PolarPlot[Cos[2 theta], {theta, Pi/4, 2 Pi - Pi/4}];
g2 = ParametricPlot[ Cos[2 theta] {Cos[theta], Sin[theta]} r, {theta, -Pi/4, Pi/4}, {r, 0, 1}, Mesh -> False];
Show[g1, g2, PlotRange -> All]
        Part of the curve r = cos(2 θ).            Mathematica code

     
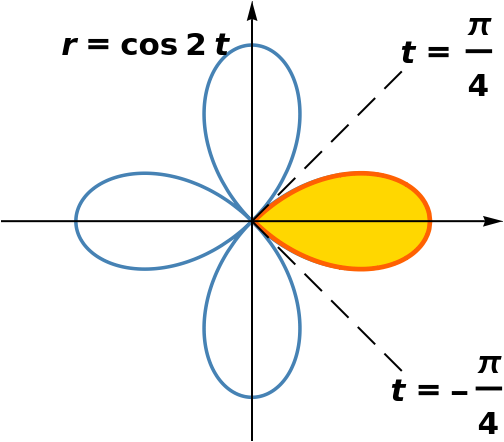txt[t_, {x_, y_}] := Style[Text[t, {x, y}], FontSize -> 30, FontWeight -> Bold] {xmin, xmax} = {-1.425, 1.425}; {ymin, ymax} = {-1.25, 1.25};
PolarPlot[Cos[2 t], {t, 0, 2 Pi}, PlotRange -> {{xmin, xmax}, {ymin, ymax}}, PlotStyle -> {ColorData["Legacy", "SteelBlue"], Thickness[0.007]}, Ticks -> None, Epilog -> {Inset[ RegionPlot[(x^2 + y^2)^(3/2) <= x^2 - y^2, {x, -0.02, 1}, {y, -1, 1}, PlotStyle -> ColorData["HTML", "Gold"], BoundaryStyle -> Directive[Thickness[0.025], ColorData["Legacy", "CadmiumOrange"]], Frame -> False, AspectRatio -> Automatic, ImageSize -> 2.6*72], {0.5, 0}], Black, Thick, Dashing[{0.045, 0.03}], Line[{{0, 0}, {0.85, 0.85}}], Line[{{0, 0}, {0.85, -0.85}}], Dashing[{}], Thick, Arrow[{{xmin, 0}, {xmax, 0}}], Arrow[{{0, ymin}, {0, ymax}}], txt[TraditionalForm[HoldForm[r == cos 2 t]], {-0.6, 1.0}], txt[TraditionalForm[HoldForm[t == Pi/4]], {1.125, 0.925}], txt[TraditionalForm[HoldForm[t == -Pi/4]], {1.125, -0.99}]}, ImageSize -> 7*72]
        One cusp from the curve r = cos(2 θ).            Mathematica code

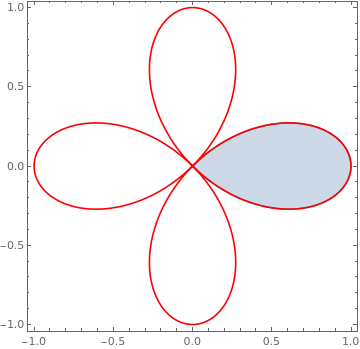      Another version:
Show[{RegionPlot[(x^2 + y^2)^(1/2) <= Cos[2 ArcTan[y/x]], {x, 0, 1}, {y, -1/2, 1/2}], PolarPlot[Cos[2 theta], {theta, 0, 2 Pi}, PlotStyle -> Red]}, PlotRange -> All]
or
Show[{RegionPlot[(x^2 + y^2)^(3/2) <= x^2 - y^2, {x, 0, 1}, {y, -1/2, 1/2}], PolarPlot[Cos[2 theta], {theta, 0, 2 Pi}, PlotStyle -> Red]}, PlotRange -> All]
or
PolarPlot[Cos[2 theta], {theta, 0, 2 Pi}, PlotStyle -> Red, Prolog -> RegionPlot[(x^2 + y^2)^(3/2) <= x^2 - y^2, {x, 0, 1}, {y, -1/2, 1/2}][[1]]]
or
s = PolarPlot[Cos[2 theta], {theta, 0, 2 Pi}];
s1 = PolarPlot[Cos[2 theta], {theta, -Pi/4, Pi/4}] /. Line -> Polygon;
Show[s, s1]
        One cusp from the curve r = cos(2 θ).            Mathematica code

 

Polar plots with fillings

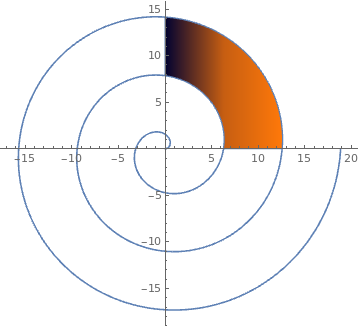One way to go around a problem to make plots with filling is to use ParametricPlot
     
parmplot = ParametricPlot[ r {Cos[t], Sin[t]}, {t, 0, Pi/2}, {r, 2 Pi + t, 4 Pi + t}, ColorFunction -> "RustTones"];
Show[ParametricPlot[t {Cos[t], Sin[t]}, {t, 0, 6 Pi}], parmplot]
        Archimede's spiral.            Mathematica code

     
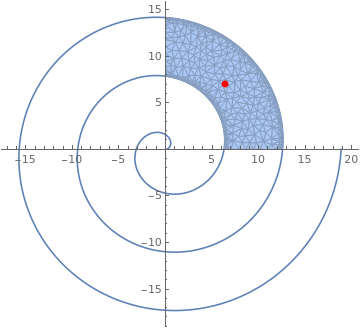cartreg = ImplicitRegion[ 2 \[Pi] < Sqrt[x^2 + y^2] - ArcTan[x, y] < 4 \[Pi] && 0 <= x <= 15 && 0 <= y <= 15, {x, y}];
regiontoplot = DiscretizeRegion[cartreg, AccuracyGoal -> 5];
NumberForm[#, {8, 5}] &@Area[regiontoplot] NumberForm[Integrate[1, {x, y} \[Element] regiontoplot], {8, 5}];
pt = RegionCentroid[regiontoplot];
Show[ParametricPlot[t {Cos[t], Sin[t]}, {t, 0, 6 Pi}], regiontoplot, Graphics[{PointSize[Large], Red, Point[pt]}]]
        Archimede's spiral with a dot.            Mathematica code

     
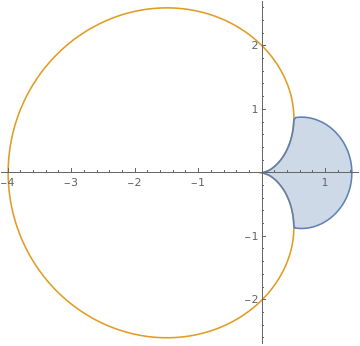Show[PolarPlot[ Evaluate[{{1, -1} Sqrt[2 Cos[t]], 2 (1 - Cos[t])}], {t, -\[Pi], \[Pi]}], RegionPlot[ Sqrt[x^2 + y^2] > 2 (1 - Cos[ArcTan[x, y]]) && Sqrt[x^2 + y^2] < Re@Sqrt[2 Cos[ArcTan[x, y]]], {x, -2, 2}, {y, -3, 3}], PlotRange -> All]
        Shading between polar graphs.            Mathematica code

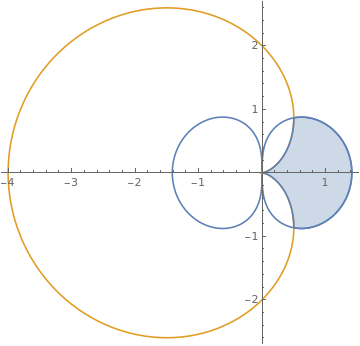      Another plot:
Show[PolarPlot[{Sqrt[2 Abs[Cos[t]]], 2 (1 - Cos[t])}, {t, -\[Pi], \[Pi]}], RegionPlot[ 4 (1 - Cos[t])^2 < r^2 < 2 Cos[t], {r, 0, 3}, {t, -Pi, Pi}, PlotPoints -> 30] /. GraphicsComplex[a_, b__] :> GraphicsComplex[#1 {Cos[#2], Sin[#2]} & @@@ a, b]]
        Shading between polar graphs.            Mathematica code

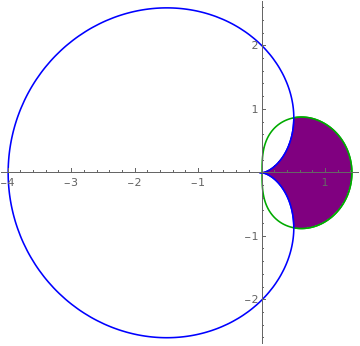      Using Cartesian coordinates:
eqns[t_] := {Sqrt[2 Cos[t]], 2 (1 - Cos[t])};
region = PolarPlot[Evaluate@eqns[t], {t, -\[Pi], \[Pi]}, RegionFunction -> Function[{x, y, t, r}, {#1 > #2} & @@ Re[eqns[t]] // First]];
pts = Cases[region, Line[x___] :> x, Infinity];
colors = {Darker@Green, Blue};
Show[PolarPlot[Evaluate@eqns[t], {t, -\[Pi], \[Pi]}, PlotStyle -> colors], ListLinePlot[pts, PlotStyle -> colors, Filling -> Axis, FillingStyle -> Purple], PlotRange -> All]
        Shading between polar graphs.            Mathematica code

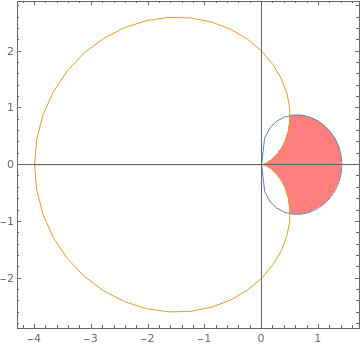      You can parameterize your polar functions on to discs, and then shade appropriately.
\[Rho][t_] := Sqrt[2 Cos[t]];
\[Sigma][t_] := 2 (1 - Cos[t]);
ParametricPlot[{{r Cos[t] \[Rho][t], r Sin[t] \[Rho][t]}, {r Cos[t] \[Sigma][t], r Sin[t] \[Sigma][t]}}, {t, -\[Pi], \[Pi]}, {r, 0, 1}, PlotStyle -> {{Opacity[.5], Red}, {Opacity[1], White}}, Mesh -> None, PlotRange -> All]
        Shading between polar graphs.            Mathematica code

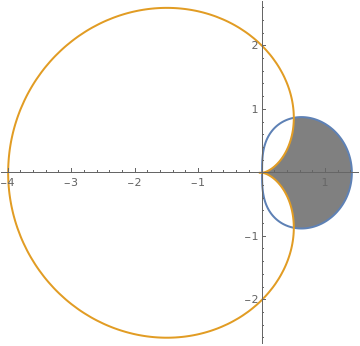      Another version:
dt = Pi/99;
pts = Join[ Table[2 (1 - Cos[t]) {Cos[t], Sin[t]}, {t, 0, -Pi/3 + dt, -dt}], Table[Sqrt[2 Cos[t]] {Cos[t], Sin[t]}, {t, -Pi/3, Pi/3, dt}], Table[2 (1 - Cos[t]) {Cos[t], Sin[t]}, {t, Pi/3, dt, -dt}]];
PolarPlot[{Sqrt[2 Cos[t]], 2 (1 - Cos[t])}, {t, -\[Pi], \[Pi]}, Prolog -> {Gray, Polygon[pts]}, PlotStyle -> Thick]
        Shading between polar graphs with contours.            Mathematica code

 

Venn Diagrams

Filling circles can be plotted using Graphics cammand. Graphics are represented as symbolic expressions, using
either"directives" or "styles":

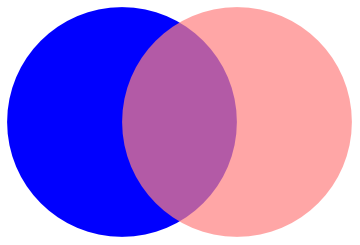
Graphics[{Blue, Disk[{0, 0}], Opacity[0.7], Pink, Disk[{1, 0}]}]

Graphics[{Style[Disk[{0, 0}], Green], Opacity[0.5], Pink, Disk[{1, 0}]}]

 

We can plot Venn diagrams using the following subroutine

 

VennDiagram2[n_, ineqs_: {}] :=
Module[{i, r = .6, R = 1, v, grouprules, x, y, x1, x2, y1, y2, ve},
v = Table[Circle[r {Cos[#], Sin[#]} &[2 Pi (i - 1)/n], R], {i, n}];
{x1, x2} = {Min[#], Max[#]} &[ Flatten@Replace[v, Circle[{xx_, yy_}, rr_] :> {xx - rr, xx + rr}, {1}]];
{y1, y2} = {Min[#], Max[#]} &[ Flatten@Replace[v, Circle[{xx_, yy_}, rr_] :> {yy - rr, yy + rr}, {1}]];
ve[x_, y_, i_] := v[[i]] /. Circle[{xx_, yy_}, rr_] :> (x - xx)^2 + (y - yy)^2 < rr^2;
grouprules[x_, y_] = ineqs /. Table[With[{is = i}, Subscript[_, is] :> ve[x, y, is]], {i, n}];
Show[If[MatchQ[ineqs, {} | False], {}, RegionPlot[grouprules[x, y], {x, x1, x2}, {y, y1, y2}, Axes -> False]],
Graphics[v], PlotLabel -> TraditionalForm[Replace[ineqs, {} | False -> \[EmptySet]]], Frame -> False]]

Then we plot two Venn diagrams:

a12 = VennDiagram2[2, Subscript[A, 1] && Subscript[A, 2]]
a1 = Graphics[Text[dogs, {-0.9, 0}]]
b1 = Graphics[Text[brown, {0.9, 0}]]
Show[a12, a1, b1]

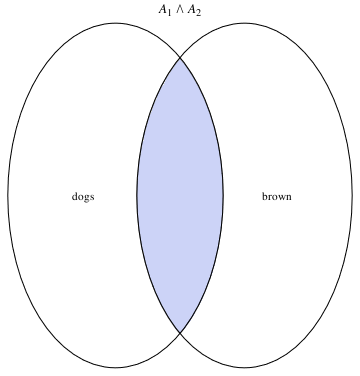
or

a32 = VennDiagram2[2, Not[Subscript[A, 1]] && Subscript[A, 2]]
a33 = VennDiagram2[2, Not[Not[Subscript[A, 1]] && Subscript[A, 2]]]

   

 

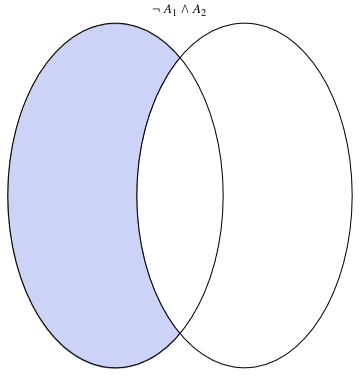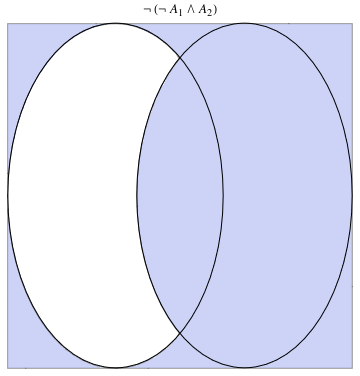Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)