Preface

This section provides an illustration of application of the Adomian decomposition method (ADM for short) to second order singular differential equations.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part VI of the course APMA0330

Glossary

Modified Laplace Decomposition Method

The Laplace transform is totally incapable of handling nonlinear equations because of the difficulties that are caused by the nonlinear terms. However, the combination of Adomian (or its modification) decomposition method with the Laplace transform can be successfully applied to solve nonlinear differential equations in semi-infinite domain. For illustration, we consider nonhomogeneous logistic equation.

Example: Consider the initial value problem for the logistic equation

\[ \dot{y} = 2\, y(t) - y^2 (t) +1+t , \qquad y(0) =1. \]
Here \( \dot{y} = \texttt{D}y = {\text d}y/{\text d}t \) is the derivative with respect to independent time variable t. We ask Mathematica to find its explicit solution, which is expressed via Airy functions:
p[t_] = y[t] /. DSolve[{y'[t] == 2*y[t] - (y[t])^2 + 1 + t, y[0] == 1}, y[t], t] // Flatten
\[ y(t) = \frac{\mbox{Ai}'(2)\,\mbox{Bi}'(2+t) + \mbox{Ai}'(2)\,\mbox{Bi}(2+t) - \mbox{Ai}'(2+t)\,\mbox{Bi}'(2) - \mbox{Ai}(2+t)\,\mbox{Bi}'(2)}{ \mbox{Ai}'(2)\,\mbox{Bi}(2+t) - \mbox{Ai}(2+t)\,\mbox{Bi}'(2)} . \]
Then we expand the above function in Maclaurin series
Series[p[t], {t, 0, 8}]
\[ y(t) = 1 + 2t + \frac{t^2}{2} - \frac{4}{3}\, t^3 - \frac{t^4}{2} + \frac{61}{60}\,t^5 + \frac{5}{9}\, t^6 - \frac{481}{630}\, t^7 - \frac{823}{1440}\, t^8 + \cdots . \]
To apply the Adomian decomposition method, let
\[ y(t) = \sum_{n\ge 0} u_n (t) , \qquad y^2 (t) = \sum_{n\ge 0} A_n (t) , \]
where An are the Adomian polynomials depending on y0, y1, ... , yn. Upon substituting into the logistic equation, it can be rewritten as
\[ \texttt{D}y(t) = \sum_{n\ge 0} \texttt{D}u_n (t) = 2\,\sum_{n\ge 0} u_n (t) - \sum_{n\ge 0} A_n (t) + 1 +t, \qquad y(0) =1. \]
Based on the recursion scheme of the ADM, we define
\[ u_0 (t) = 1 + t + \frac{t^2}{2} , \]
as the solution to the initial value problem \( \dot{y} = 1+t , \ y(0) =1 . \) Then next terms un+1 are obtaind from the recursive initial value problems:
\[ \dot{u}_{n+1} = 2\,u_n - A_n (t), \qquad u_{n+1} (0) =0, \qquad n=0,1,2,\ldots . \]
Note that the Adomian polynomials An(t) for the quadratic nonlinearty are written as
\begin{eqnarray*} A_0 (t) &=& u_0^2 (t) = \left( 1 + t + \frac{t^2}{2} \right)^2 , \\ A_1 (t) &=& 2\,u_0 (t)\,u_1 (t) = \left( 2 + 2t + t^2 \right) u_1 (t) , \\ A_2 (t) &=& 2\,u_0 (t)\,u_2 (t) + u_1^2 (t) = \left( 2 + 2t + t^2 \right) u_2 (t) + u_1^2 (t) , \\ A_3 (t) &=& 2\,u_0 (t)\,u_3 (t) + 2\,u_1 (t)\,u_2 (t) = \left( 2 + 2t + t^2 \right) u_3 (t) + 2\,u_1 (t)\,u_2 (t) , \\ A_4 (t) &=& 2\,u_0 (t)\,u_4 (t) + 2\,u_1 (t)\,u_3 (t) + u_2^2 = \left( 2 + 2t + t^2 \right) u_4 (t) + 2\,u_1 (t)\,u_3 (t) + u_2^2 , \\ \end{eqnarray*} and so on. Mathematica helps us with solving these recursive IVPs:
DSolve[{y'[t] == 2*(1 + t + t^2/2) - (1 + t + t^2/2)^2, y[0] == 0}, y[t], t]// Flatten
u[1][t_] = y[t] /. %
1/60 (60 t - 20 t^3 - 15 t^4 - 3 t^5)
Next iterations:
DSolve[{y'[t] == 2*u[1][t] - 2*u[1][t]*(1 + t + t^2/2), y[0] == 0}, y[t], t]// Flatten
u[2][t_] = y[t] /. %
(-960 t^3 - 360 t^4 + 192 t^5 + 200 t^6 + 72 t^7 + 9 t^8)/1440
and
DSolve[{y'[t] == 2*u[2][t] - 2*u[2][t]*(1 + t + t^2/2) -(u[1][t])^2, y[0] == 0}, y[t], t]// Flatten
u[3][t_] = y[t] /. %
(1/4989600)(-1663200 t^3 + 1995840 t^5 + 1386000 t^6 - 19800 t^7 - 360360 t^8 - 185570 t^9 - 43659 t^10 - 3969 t^11)
Other components can be calculated similarly.

Now we add all terms to obtain Adomian approximation and plot it along with the true solution.

phi3[t_]=Simplify[(1 + t + t^2/2) + u[1][t] + u[2][t]+u[3][t]]
1 + 2 t + t^2/2 - (4 t^3)/3 - t^4/2 + (29 t^5)/60 + (5 t^6)/12 + ( 29 t^7)/630 - (19 t^8)/288 - (241 t^9)/6480 - (7 t^10)/800 - ( 7 t^11)/8800
Plot[{Callout[p[t], "exact"], Callout[phi3[t], "ADM approximation"]}, {t,0,1.8}, PlotStyle->Thick]
True solution and Adomian approximation with N=3 terms.
■
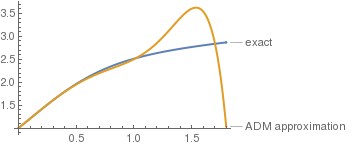
  1. Adam, B.A.A., A Comparative Study of Successive Approximations Method and He--Laplace Method, British Journal of Mathematics & Computer Science, 2015, Vol. 6, No. 2, pp. 129--145.
  2. Adrianov, I.V., Olevskii, V.I. and Tokarzewski, S., A modified Adomian’sdecomposition method, Applied Mathematics and Mechanics (English Edition), 1998, Vol. 62, No 2, pp. 309--314. https://doi.org/10.1016/S0021-8928(98)00040-9
  3. Berna Bülbül and Mehmet Sezer, Numerical Solution of Duffing Equation by Using an Improved Taylor Matrix Method, 2013, Journal of Applied Mathematics, 2013, Volume 2013, Article ID 691614, 6 pages; http://dx.doi.org/10.1155/2013/691614
  4. El-Tawill, M.A., A.A. Bahnasawi and A. Abdel-Naby, 2004. Solving Riccati differential equation using Adomian’s decomposition method, Applied Mathematics and Computation, 2004, 157: 503-514.
  5. Hosseinzadeh, H., H. Jafari and M. Roohani, 2010. Application of Laplace decomposition method for solving Klein-Gordon Equation, World Applied Sciences Journal, 2010, Vol. 8, No. 9, pp. 1100--1105.
  6. Islam, S., Y. Khan, N. Faraz and F. Austin, 2010. Numerical Solution of Logistic Differential Equations by using the Laplace Decomposition Method, World Applied Sciences Journal, 2010, Vol. 8, No. 9, pp. 1100--1105.
  7. Khan, Y., “An effective modification of the Laplace decomposition method for nonlinear equations”, International Journal of Nonlinear Sciences and Numerical Simulation, 2009, 10(11-12), 1373- 1376.
  8. Khan, Y. and Faraz, N., 2010. A new approach to differential difference equations, Journal of Advanced Research, 2010, Vol. 2, No. 2, pp. 1--12.
  9. Khan, Y. and Faraz, N., “Application of modified Laplace decomposition method for solving boundary layer equation”, Journal of King Saud University (Science), 2011, 23, 115-119
  10. Khan, Y., Faraz, N., and Yildirim, A., Series Solution for Unsteady Gas Equation via MLDM-Padé Technique, World Applied Sciences Journal, 2010, Vol. 10, No. 12, pp. 1452--1456,
  11. Khan, M. and Hussain, M., Application of Laplace decomposition method on semi-infinite domain, Numerical Algorithms, 2011, Volume 56, Issue 2, pp. 211--218.
  12. Khuri, S.A., A Laplace decomposition algorithm applied to a class of nonlinear differential equations, Journal of Applied Mathematics, 2001, Volume 1, Issue 4, Pages 141--155; http://dx.doi.org/10.1155/S1110757X01000183
  13. Khuri, S.A., A new approach to Bratus problem, Applied Mathematics and Computation, 2004, 147 (1) (2004) 131–136.
  14. M. A. Koroma, Z. Chuangyi, A. F., Kamara, and A. M. H. Conteh, A modified Laplace decomposition algorithm solution for Blasius’ boundary layer equation of the flat plate in a uniform stream, World Academy of Science, Engineering and Technology, 2013, doi: 10.5281/zenodo.1087109
  16. Manafianheris, J., Solving the integro-differential equations using the modified Laplace Adomian decomposition method, Journal of Mathematical Extension, 2012, Vol. 6, No. 1, pp. 65--79.
  17. Mishra, H.K. and Nagar, A.K., He-Laplace Method for Linear and Nonlinear Partial Differential Equations, Journal of Applied Mathematics, Volume 2012, Article ID 180315, 16 pages; http://dx.doi.org/10.1155/2012/180315
  20. Noor, M.A. and Mohyud-Din, S.T., Modified Variational Iteration for a Boundary Layer Problem in Unbounded Domain, International Journal of Nonlinear Science, 2009, Vol. 7, No. 4, pp. 426--430.
  21. Patel, H.S. and Meher, R., Application of Laplace Adomian Decomposition Method for the soliton solutions of Boussinesq-Burger equations, International Journal of Advances in Applied Mathematics and Mechanics, 2015, Vol. 3, No. 2, pp. 50--58.
  23. Rashidi, M. M. “The modified differential transforms method for solving MHD boundary-Layer equations”, Computer Physics Communications, 2009, Vol. 180, Issue 11, pp. 2210--2217. https://doi.org/10.1016/j.cpc.2009.06.029
  24. Rashidi, M. M. and Erfani, E., "The modified differential transform method for investigating nano boundary-layers over stretching surfaces," International Journal of Numerical Methods for Heat and Fluid Flow, 2011, Vol. 21, No. 7, pp. 864--883; doi: 10.1108/09615531111162837
  25. Vahidi, A.R., Babolian, E., and Azimzadeh, Z., A Comparative Study of Numerical Methods for Solving the Riccati Equation, World Applied Sciences Journal, 2012, Vol. 16, No. 7, pp. 921--925; doi:
  26. Wang, K. and Liu, S., Application of new iterative transform method and modified fractional homotopy analysis transform method for fractional Fornberg-Whitham equation, Journal of Nonlinear Science and Applications, 2016, Vol. 9, pp.2419--2433.
  27. Wazwaz, A.M., The modified decomposition method and Pade ́approximants for solving Thomas- Fermi equation, Applied Mathematics and Computation, 1999, Vol. 105, pp. 11--19.
  28. Wazwaz, A.M., 2010. The combined Laplace transform-Adomian decomposition method for handling nonlinear Volterra integro-differential equations, Applied Mathematics and Computation, 2010, 216: 1304-1309.
  29. Xu, L., He’s homotopy perturbation method for a boundary layer equation in unbounded domain, Computers & Mathematics with Applications, , 54: 1067-1070.
  30. Yusufoglu, E., 2006. Numerical solution of Duffing equation by the Laplace decomposition algorithm, Applied Mathematics and Computation, 2006, 177, 572--580;

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)