Preface

This section gives an introduction to a particular class of iterative root finding methods, called open methods. As opposed to closed or bracketing methods (discussed in the previous section), open methods do not necessarily bracket a root; therefore, they may diverge as computation progresses, but when they do converge, open methods are usually so much faster than bracketing methods. The root finding methods are applied for solving nonlinear equations of the form f(x) = 0. These are the problems of applied mathematics that occur most often for which explicit solutions are not available. We present some iterative algorithms for the determination of roots of these equations to any specified degree of accuracy. There are two large classes of iterative numerical methods for root finding, namely those that either involve a usage of derivatives or not.

We begin with Newton's method and its discretization---the secant method, which provide root-finding algorithms that use a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite-difference approximation of Newton's method. The section also contains some iterative algorithms to find a root of a nonlinear equation f(x) = 0 of order two and larger.

A concept of the the algorithm (Newton.1) was introduced by Isaac Newton in 1669, who used it to solve a cubic equation numerically. Before Newton other people also suggested analogous methods. The essential ideas of the method can be found in manuscripts of the fourteenth century written by the Persian astronomer and mathematician Ghiyāth al-Kāshī (1380--1429). His method of root-finding was not known by his contemporary mathematicians. We know that the English mathematician Henry Briggs (1561--1630) also published a work involving the numerical solution of polynomial equation in 1633. In 1685, John Wallis (1616--1703) described a method which---Willis said---was invented by I.Newton. However, the first systematic description of the method was given by J.Raphson in Aequationum Universalis, seu Ad Aequationes Algebraicas Resolvendas Methodus Generalis, & Expedita, Ex Nova Infinitarum Serierum Methodo, Deducta et Demonstrata (London, 1690).

The basic idea behind Newton's method is quite straightforward. Let x_n denote the most recent approximation to zero, α, of the function f. Replace f by its tangent line approximation that goes through the point x_n and takes the x-intercept of the tangent line as the next approximation x_n+1 to the root.

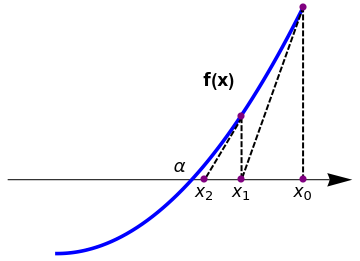
		plot = Plot[1*x^2, {x, 0, 1}, AspectRatio -> 1, PlotStyle -> {Thickness[0.01], Blue}, Axes -> False, Epilog -> {PointSize[0.03], Pink, Point[{{0, 0}, {2, 2.8}}]}, PlotRange -> {{-0.5, 1.2}, {-0.2, 1.4}}]; arrow = Graphics[{Arrowheads[0.07], Arrow[{{-0.2, 0.3}, {1.2, 0.3}}]}]; l1 = Graphics[{Thick, Dashed, Line[{{1, 1}, {0.75, 0.3}}]}]; l2 = Graphics[{Thick, Dashed, Line[{{0.75, 0.55}, {0.6, 0.3}}]}]; l3 = Graphics[{Thick, Dashed, Line[{{1, 1}, {1, 0.3}}]}]; l4 = Graphics[{Thick, Dashed, Line[{{0.75, 0.55}, {0.75, 0.3}}]}]; t2 = Graphics[{Black, Text[Style[Subscript[x, 0], 16], {1, 0.25}]}]; t3 = Graphics[{Black, Text[Style[Subscript[x, 1], 16], {0.75, 0.25}]}]; t4 = Graphics[{Black, Text[Style[Subscript[x, 2], 16], {0.6, 0.25}]}]; t5 = Graphics[{Black, Text[Style[\[Alpha], 16], {0.5, 0.35}]}]; t9 = Graphics[{Black, Text[Style["f(x)", Bold, 16], {0.66, 0.7}]}]; Show[arrow, plot, l1, l2, l3, l4, t2, t3, t4, t5, t9, Epilog -> {PointSize[0.02], Purple, Point[{{0.6, 0.3}, {0.75, 0.555}, {0.75, 0.3}, {1, 0.3}, {1, 1}}]}]
Newton's method.		Mathematica code

The tangent line in Newton's method can be seen as the first degree polynomial approximation of f(x) at x = x_n. Though, Newton's formula is simple and fast with quadratic convergence. It may fail miserably if at any stage of computation the derivative of the function f(x) is either zero or very small. Therefore, it has stability problems as it is very sensitive to the initial guess.    ■

If the root being sought has multiplicity greater than one, the convergence rate is merely linear. However, if the multiplicity m of the root is known, the following modified algorithm preserves the quadratic convergence rate

Newton's method can be realized with the aid of the FixedPoint command:

The Babylonians had an accurate and simple method for finding the square roots of numbers. This method is also known as Heron's method, after the Greek mathematician who lived in the first century AD. Indian mathematicians also used a similar method as early as 800 BC. The Babylonians are credited with having first invented this square root method, possibly as early as 1900 BC.

Newton's method is an extremely powerful technique—in general, the convergence is quadratic: when the algorithm approaches the root; the difference between the root and the approximation is squared (the number of accurate digits roughly doubles) at each step. It has been shown that both, Newton's method as well as Steffensen's method, are optimal algorithms of the second order that require the least possible number of arithmetic operations. Therefore, the Newton--Raphson iteration scheme is very popular in applications and this method is usually applied first when root should be determined. However, for a multiple root, Newton's method has only linear order of convergence. A procedure is known to speed up its order (see Varona's paper).

Sometimes Newton’s method does not converge; the first above theorem guarantees that δ exists under certain conditions, but it could be very small. Newton's method is a good way of approximating solutions, but applying it requires some intelligence. You must beware of getting an unexpected result or no result at all. So why would Newton’s method fail? Well, the derivative may be zero at the root (degenerate when the function at one of the iterated points has zero slope); the function may fail to be continuously differentiable; one of the iterated points x_n is a local minimum/maximum of f; and you may have chosen a bad starting point, one that lies outside the range of guaranteed convergence. It may happen that the Newton--Raphson method may start at an initial guess close to one root, but further iterates can jump to a location of one of several other roots. Depending on the context, each one of these may be more or less likely. Degenerate roots (those where the derivative is 0) are "rare" in general and we do not consider this case.

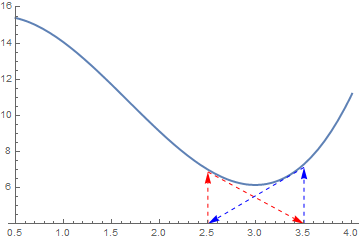
		Finally, there is a chance that Newton's method will cycle back and forth between two value and never converge at all. This failure is illustrated in the Figure below. a1 = {Arrowheads[Medium], Arrow[{{2.5, 6.875}, {3.5, 4}}]} a2 = {Arrowheads[Medium], Arrow[{{3.5, 7.125}, {2.5, 4}}]} b1 = Graphics[{Dashed, Red, a1}] b2 = Graphics[{Dashed, Blue, a2}] f[x_] = x^3 - 5*x^2 + 3.05*x + 15 graph = Plot[f[x], {x, 0.5, 4}, PlotRange -> {4, 16}, PlotStyle -> Thick] v1 = {Arrowheads[Medium], Arrow[{{2.5, 4}, {2.5, 6.875}}]} v2 = {Arrowheads[Medium], Arrow[{{3.5, 4}, {3.5, 7.125}}]} b11 = Graphics[{Dashed, Red, v1}] b22 = Graphics[{Dashed, Blue, v2}] Show[graph, b1, b2, b11, b22]
Newton's method may loop.		Mathematica code

Example 4: This example is a cautionary one. Consider the function \( f(x) = x\,e^{-x^2} \) that obviously has a root at x = 0. However, if your starting point exceeds the root of the equation \( f'(x) = 0 , \) which is \( x_0 = 1/\sqrt{2} \approx 0.707107 , \) then Newton's algorithm diverges.

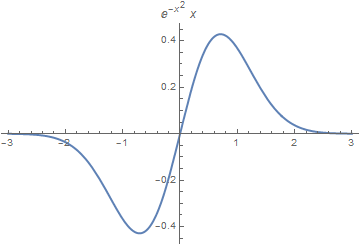
		Finally, there is a chance that Newton's method will cycle back and forth between two values and never converge at all. This failure is illustrated in Figure below. f[x_]= x*Exp[-x^2] D[x*Exp[-x^2], x] FindRoot[E^-x^2 - 2 E^-x^2 x^2 == 0, {x, 1}] Plot[x*Exp[-x^2], {x, -3, 3}, PlotStyle -> Thick, PlotLabel -> x*Exp[-x^2]] p[0] = 0.8 Do[Print["k= ", k, " " , "p= " , p[k] = p[k - 1] - p[k - 1]/(1 - 2*p[k - 1])], {k, 1, 15}]
Graph of the exponential function.		Mathematica code

The derivative of f(x) is zero at \( x = 1/\sqrt{2} \approx 0.707107 , \) and negative for x > 0.707107.

Simplify[D[f[x], x]*Exp[x^2]]

1 - 2 x^2

N[1/Sqrt[2]]

0.707107

For any initial guess x₀ > 0.707107, the Newton's iterates move away from the zero; so it diverges.    ■

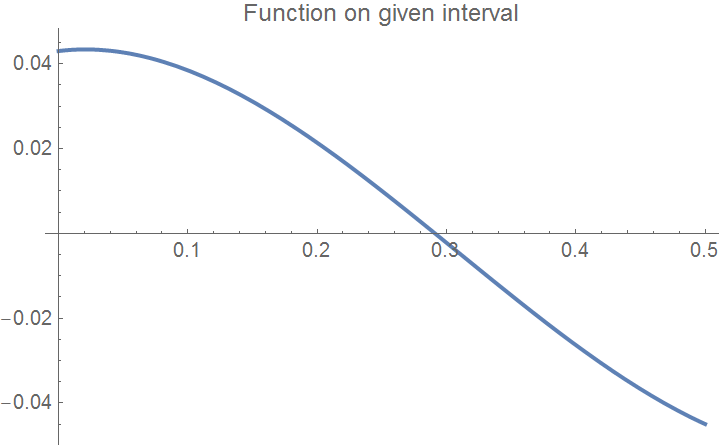
Example 5: Consider the cubic function \( f(x) = x^3 - 0.926\,x^2 + 0.0371\,x + 0.043 . \) First we plot the function, and then define the range of 'x' where you want to see its null.

f[x_] := x^3 - 0.926*x^2 + 0.0371*x + 0.043
Plot[f[x], {x, 0, 1}, PlotStyle -> {Thick, Blue}]
xbegin = 0; xend = 0.5;
curve = Plot[f[x], {x, xbegin, xend}, PlotLabel ->
"Function on given interval", PlotStyle -> {Thick, FontSize -> 11}]

Taking initial guess

x0 = 0.3

we start Newton's iteration. Because this method uses a line tangent to the function at the initial guess, we must calculate the derivative of the function to find the slope of the line at this point. We will denote by g(x) the derivative of the function f(x).

g[x_] := f'[x]

maxi = f[xend]; mini = f[xbegin];
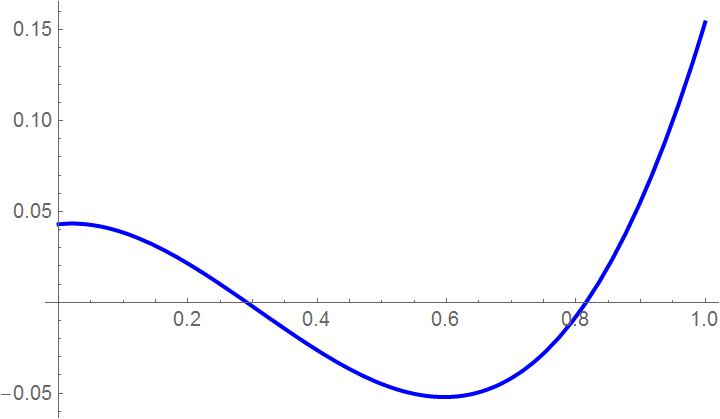step = (xend - xbegin)/10;
Do[ If[f[i] > maxi, maxi = f[i]];
If[f[i] < mini, mini = f[i]], {i, xbegin, xend, step}];
tot = maxi - mini
mini = mini - 0.1*tot; maxi = maxi + 0.1*tot;

We begin with the first Newton's iteration.

x1 = x0 - f[x0]/g[x0]

Out[23]= 0.291107

Then we plot the tangent line along with the given function and bounds for the root.

ea = Abs[(x1 - x0)/x1*100]

Out[24]= 3.05502

tanline[x_]:=f[x0]+((0-f[x0])/(x1-x0))*(x-x0)
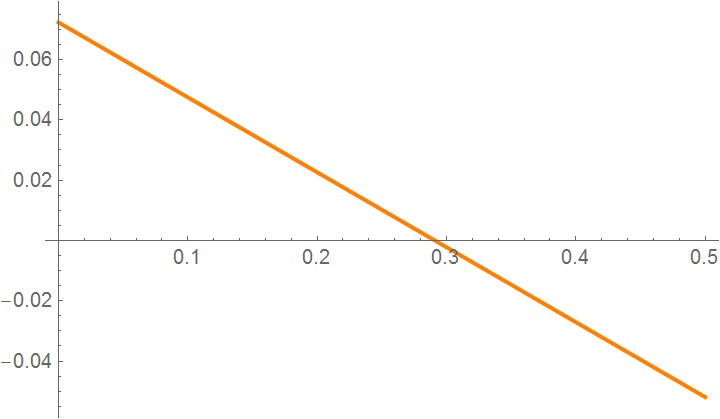
tline = Plot[tanline[x], {x, xbegin, xend}, PlotStyle -> {Thick, Orange}]
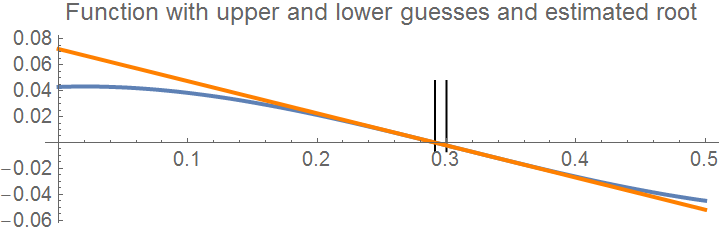
Show[Graphics[Line[{{x0, maxi}, {x0, mini}}]], curve,
Graphics[Line[{{x1, maxi}, {x1, mini}}]], tline, Axes -> True,
PlotLabel -> "Function with upper and lower guesses and estimated root", PlotStyle -> {FontSize -> 10}]

Now we make the second iteration.

x2=x1-f[x1]/g[x1]

Out[25]= 0.291096

Then we compare its value with the actual root obtained using a standard Mathematica command.

s = FindRoot[f[x] == 0, {x, 0.3}]
NumberForm[N[s], 20]

Out[26]= {x -> 0.291096}

which is a more accurate approximation to the root: 0.291095502695723. Indeed,

f[0.291095502695723]

Out[28]= 0.

This is the zero within Mathematica accuracy. So we see that two iterations are enough to get at least six accurate decimal places. For instance, the third iteration yields

x3=x2-f[x2]/g[x2]

Out[29]= 0.291095502695723

   ■

Example 6: We reconsider the function \( f(x) = e^x\, \cos x - x\, \sin x \) that has one root within the interval [0,3]. We define the range of x:

xa = 0; xb = 3;

We break the guess interval [0,3] into 10 uniform parts and calculate the values of the given function at each end point of these subintervals.

maxi = f[xa]; mini = f[xb];
step = (xb - xa)/10;
x[0] = xa;
Do[ x[i] = x[i - 1] + step; If[f[x[i]] > maxi, maxi = f[x[i]]; If[f[x[i]] < mini, mini = f[x[i]]]];
Print["i= ", i, ", x[i]= ", x[i], ", f[x[i]]= ", N[f[x[i]]]]; , {i, 1, 10}]

So we see that the first root is within the interval [6/5, 3/2]. Let us take the middle of the interval as our first guess:

x0 = (6/5 + 3/2)/2

Out[2]= 27/20

which is 1.35. We set the maximum number of iterations to be 4:

nmaximum = 4

Then we define the derivative of the function f(x) which we denote by g(x).

f[x_] := Exp[x]*Cos[x] - x*Sin[x]
g[x_] := f'[x]

Now we find the actual solution using Mathematica (this is an approximation as well, but with good accuracy)

s = FindRoot[f[x] == 0, {x, 1.35}]
actual = x /. s
NumberForm[N[actual], 20]

Out[7]= 1.2253937841236207

We apply the Newton--Raphson method to generate the values of the roots, true error, absolute relative true error, approximate error, absolute relative approximate error, and the least number of significant digits that are correct in the estimated root as a function of number of iterations.

Clear[xr]; SetPrecision[xr, 40]
Array[xr, nmaximum];

We generate the sequence of root approximations.

For[i = 1; xr[0] = N[x0], i <= nmaximum, i++,
xr[i] = xr[i - 1] - f[xr[i - 1]]/g[xr[i - 1]]]

Absolute true error:

Array[Et, nmaximum];
For[i = 1, i <= nmaximum, i++, Et[i] = Abs[actual - xr[i]]]

Absolute relative true error:

Array[et, nmaximum];
For[i = 1, i <= nmaximum, i++, et[i] = Abs[Et[i]/actual*100]]

Absolute approximate error:

Array[Ea, nmaximum];
For[i = 1, i <= nmaximum, i++,
If[i <= 1, Ea[i] = Abs[xr[i] - x0], Ea[i] = Abs[xr[i] - xr[i - 1]]]]

Absolute relative approximate error:

Array[ea, nmaximum];
For[i = 1, i <= nmaximum, i++, ea[i] = Abs[Ea[i]/xr[i]*100]]

Significant digits at least correct.

Array[sigdig, nmaximum];
For[i = 1, i <= nmaximum, i++,
If[(ea[i] >= 5) || (i <= 1), sigdig[i] = 0,
sigdig[i] = Floor[(2 - Log[10, Abs[ea[i]/0.5]])]]]

Graphs:

xrplot = Table[xr[i], {i, 1, nmaximum}];
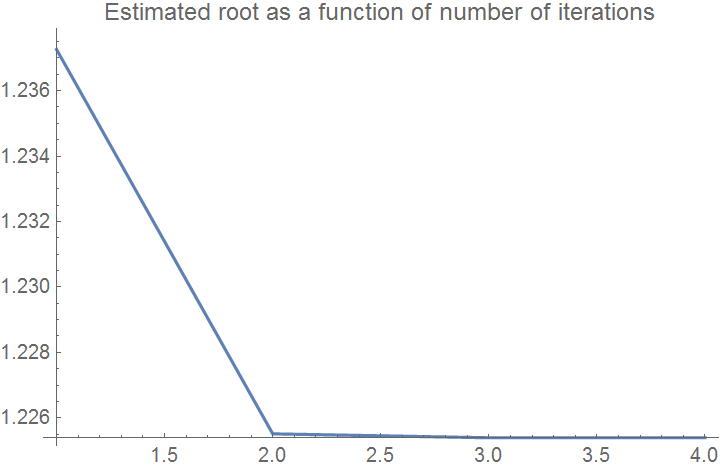
ListPlot[xrplot, Joined -> True, PlotRange -> All,
AxesOrigin -> {1, Min[xrplot]},
PlotLabel -> "Estimated root as a function of number of iterations"]

   ■

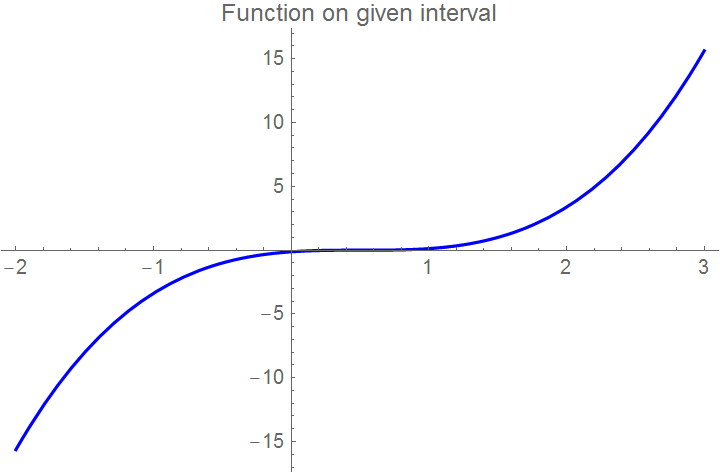
Example 7: This example shows that Newton's method may converge slowly due to an inflection point occurring in the vicinity of the root. Let us consider the function \( f(x) = (x-0.5)^3 . \) First we define the function and its derivative:

f[x_] := (x-0.5)^3
g[x_] := f'[x]

Then we plot the function:

xbegin = -2; xend = 3;
curve = Plot[f[x], {x, xbegin, xend},
PlotLabel -> "Function on given interval", PlotStyle -> {FontSize -> 11, Blue}]

Next we define the initial guess and maximum number of iterations.

x0 = -1; nmaximum = 10;

First iteration.

x1 = x0 - f[x0]/g[x0]

Out[16]= -0.5

ea = Abs[(x1 - x0)/x1*100]

Out[17]= 100

tanline[x_] := f[x0] + ((0 - f[x0])/(x1 - x0))*(x - x0)
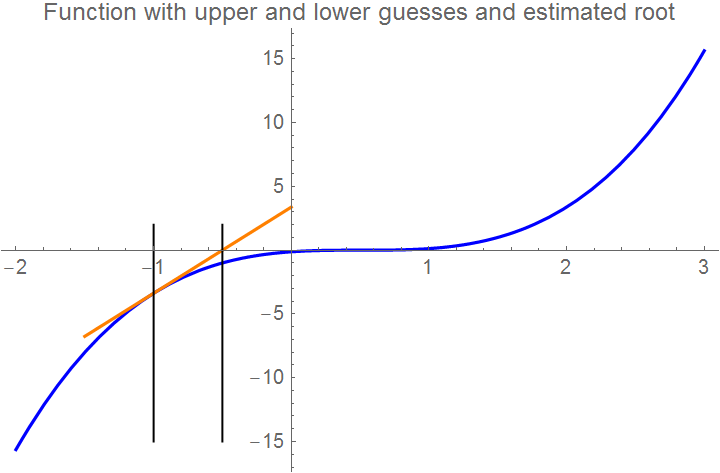
tline = Plot[tanline[x], {x, -1.5, 0.0}, PlotStyle -> {Orange}];
Show[curve, tline, Graphics[Line[{{x0, 2}, {x0, -15}}]],
Graphics[Line[{{x1, 2}, {x1, -15}}]], Axes -> True, PlotRange -> All,
PlotLabel -> "Function with upper and lower guesses and estimated root", PlotStyle -> {FontSize -> 10}]

We start the second iteration.

x2 = x1 - f[x1]/g[x1]

Out[24]= -0.166667

ea = Abs[(x2 - x1)/x2*100]

Out[25]= 200

Then we plot tangent line.

tanline[x_]:=f[x1]+((0-f[x1])/(x2-x1))*(x-x1)
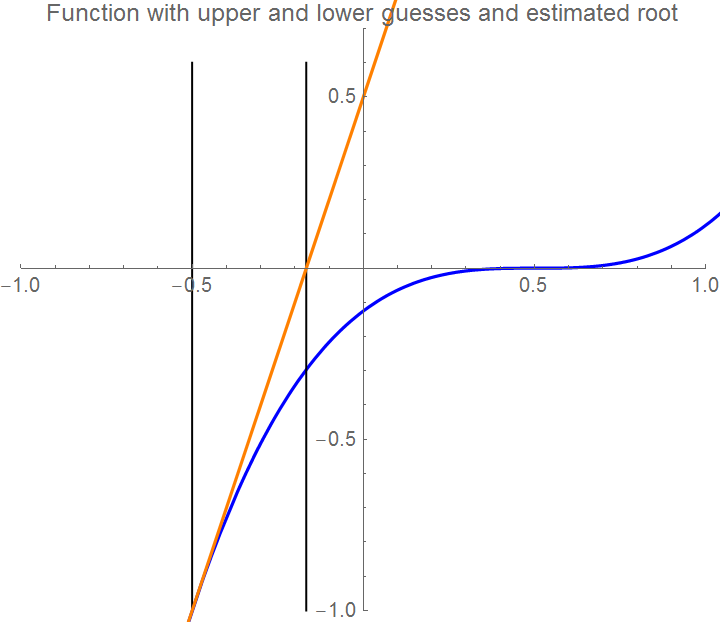
tline = Plot[tanline[x], {x, -1, 1}, PlotStyle -> {Orange}];
Show[Graphics[Line[{{x1, 0.6}, {x1, -1}}]], curve,
Graphics[Line[{{x2, 0.6}, {x2, -1}}]], tline, Axes -> True,
PlotLabel -> "Second iteration and estimated root", PlotStyle -> {FontSize -> 10}, PlotRange -> {{-1, 1}, {-1, 0.7}}]

Third iteration,

x3 = x2 - f[x2]/g[x2]

Out[38]= 0.0555556

ea = Abs[(x3 - x2)/x3*100]

Out[39]= 400

and then fourth iteration.

x4=x3-f[x3]/g[x3]

Out[40]= 0.203704

ea = Abs[(x4 - x3)/x4*100]

Out[41]= 72.7273

So we see that convergence is very slow. ■    ■

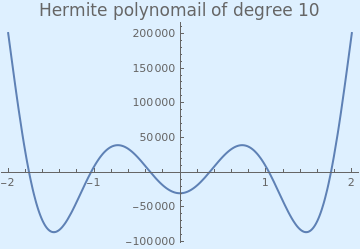
Example: Consider the Hermite polynomial of degree 10:

\[ H_{10} (x) = 1024\,x^{10} - 23040\, x^8 + 161280\,x^6 - 403200\,x^4 + 302400 \,x^2 - 30240. \]

		We plot the Hermite polynomial with the following Mathematica code: Plot[HermiteH[10, x], {x, -2, 2}, PlotStyle -> Thick, PlotLabel -> Style["Hermite polynomial of degree 10", FontSize -> 16], Background -> LightBlue]
Hermite polynomial of degree 10.		Mathematica code

Since these polynomials were discovered by P.Chebyshev, they are called also Chebyshev--Hermite polynomials. Since the Hermite polynomial has negative value at x = 0

HermiteH[10, 0]

-30240

and positive value at x = 1

HermiteH[10, 1]

8224

we know that one of its roots belongs to the interval [0,1]. So we start with first two approximations x₀ = 0 and x₁ = 1. The middle point is obviously u = 0.5. According to Ridders' formula, our next iteration is

\[ x_2 = \frac{1}{2} - \frac{1}{2} \cdot \frac{H_{10}(0.5)}{\sqrt{H_{10}^2 (0.5) - H_{10}(0) \cdot H_{10}(1)}} = 0.090012 . \]

x2 = 1/2 - 1/2*HermiteH[10, 0.5]/Sqrt[HermiteH[10, 0.5]^2 - HermiteH[10, 0]*HermiteH[10, 1]]

0.090012

   ■

A palpable drawback of Newton's method is that it requires us to have a formula for the derivative of f. For classroom examples this is not an issue, but in the "real world" it can be. Suppose, for example, that f is instead "defined" by a separate subprogram that uses about 1,000 lines of involved computer code. Even if we could theoretically write a formula for the derivative from which f' could be constructed, is this a practical task to set for ourselves?

One obvious way to deal with this problem is to use an approximation to the derivative with the Newton formula

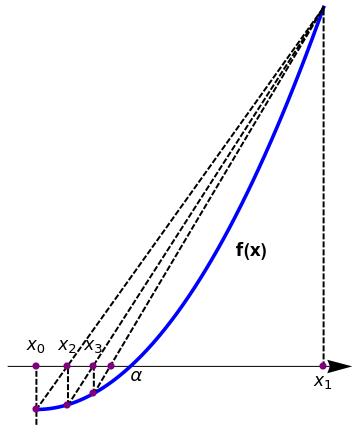
		plot = Plot[0.7*x^2, {x, 0, 2}, AspectRatio -> 1, PlotStyle -> {Thickness[0.01], Blue}, Axes -> False, Epilog -> {PointSize[0.03], Pink, Point[{{0, 0}, {2, 2.8}}]}, PlotRange -> {{-0.5, 2.2}, {-0.2, 4.4}}]; line = Graphics[{Thick, Dashed, Black, Line[{{0, 0}, {2, 2.8}}]}]; arrow = Graphics[{Arrowheads[0.07], Arrow[{{-0.2, 0.3}, {2.2, 0.3}}]}]; l1 = Graphics[{Thick, Dashed, Line[{{0, -0.1}, {0, 0.3}}]}]; l2 = Graphics[{Thick, Dashed, Line[{{0.22, 0.03}, {2, 2.8}}]}]; l3 = Graphics[{Thick, Dashed, Line[{{2, 0.3}, {2, 2.8}}]}]; l4 = Graphics[{Thick, Dashed, Line[{{0.22, 0.03}, {0.22, 0.3}}]}]; l5 = Graphics[{Thick, Dashed, Line[{{0.4, 0.11}, {0.4, 0.3}}]}]; l6 = Graphics[{Thick, Dashed, Line[{{0.4, 0.11}, {2, 2.8}}]}]; t1 = Graphics[{Black, Text[Style[Subscript[x, 0], 16], {0, 0.45}]}]; t2 = Graphics[{Black, Text[Style[Subscript[x, 1], 16], {2, 0.2}]}]; t3 = Graphics[{Black, Text[Style[Subscript[x, 2], 16], {0.22, 0.45}]}]; t4 = Graphics[{Black, Text[Style[\[Alpha], 16], {0.7, 0.23}]}]; t5 = Graphics[{Black, Text[Style[Subscript[x, 3], 16], {0.4, 0.45}]}]; t8 = Graphics[{Black, Text[Style["f(b)", {1.08, 1}]]}]; t8 = Graphics[{Black, Text[Style["f(b)", {1.08, 1}]]}]; Show[arrow, plot, line, l1, l2, l3, l4, l5, l6, t1, t2, t3, t4, t5, t8, t9, Epilog -> {PointSize[0.02], Purple, Point[{{0, 0}, {0, 0.3}, {0.22, 0.3}, {0.22, 0.03}, {0.4, 0.3}, {0.4, 0.11}, {0.52, 0.3}, {2, 0.3}}]}]
Secant algorithm.		Mathematica code

The secant method is consistent with Newton's method, and its error is proportional to h = x_k+1 - x_k. Thus, if we assume that the iteration is converging (so that h = x_k+1 - x_k → 0), then the secant method becomes more and more like Newton's method. Hence, we expect rapid convergence of the secant iterates near the root α. The secant method has a number of advantages over Newton's method. Not only does it not require the derivative, but it can be coded in such a way as to require only a single function evaluation per iteration. Newton requires two: one for the function and one for the derivative. Thus, the secant method is about half as costly per step as Newton's method.

When the secant method is applied to find a square root of a positive number A, we get the formula

Input: x0 and x1
Set y0=f(x0) and y1=f(x1)
Do 
   x=x1-y1*(x1-x0)/(y1-y0)
   y=f(x)
   Set x0=x1 and x1=x
   Set y0=y1 and y1=y
Until |y1| < tol

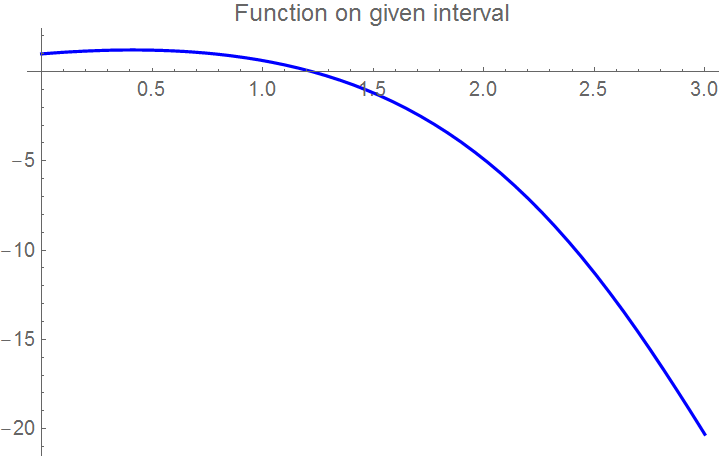
Example 9: We consider the function \( f(x) = e^x\, \cos x - x\, \sin x \) that has one root within the interval [0,3]. We define the range of x:

f[x_] := Exp[x]*Cos[x] - x*Sin[x]
xa = 0; xb = 3;

and then plot the function:

curve = Plot[f[x], {x, xa, xb},
PlotLabel -> "Function on given interval", PlotStyle -> {FontSize -> 11, Blue}]

We make lower initial guess and upper initial guess:

xguess1 = 1.0; xguess2 = 2.0;

and then plot the function along with two guess bounds:

Show[Graphics[Line[{{xguess2, maxi}, {xguess2, mini}}]], curve,
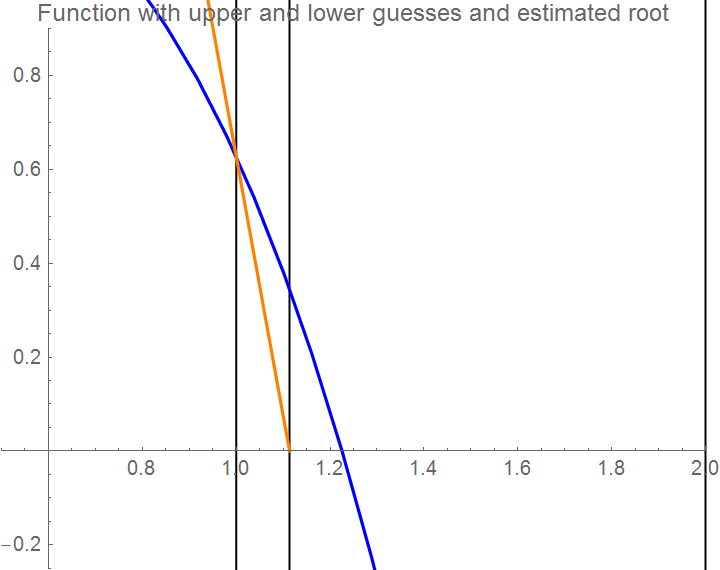
Graphics[Line[{{xguess1, maxi}, {xguess1, mini}}]], Axes -> True,
PlotLabel -> "Function with upper and lower guesses",
PlotStyle -> {FontSize -> 10}, PlotRange -> {{0.7, 2}, {-0.2, 0.4}}]

We make the first iteration:

x1 = xguess2 - (f[xguess2]*(xguess1 - xguess2))/(f[xguess1] - f[xguess2])

1.11361

Plot of the line through two guess points:

m = (f[xguess2] - f[xguess1])/(xguess2 - xguess1);
secantline[x_] = m*x + f[xguess2] - m*xguess2;
sline = Plot[secantline[x], {x, xa, x1}, PlotStyle -> {Orange}]
Show[Graphics[Line[{{xguess2, maxi}, {xguess2, mini}}]],
Graphics[Line[{{x1, maxi}, {x1, mini}}]], curve,
Graphics[Line[{{xguess1, maxi}, {xguess1, mini}}]], sline,
Axes -> True, PlotLabel -> "Function with upper and lower guesses and estimated root",
PlotStyle -> {FontSize -> 10}, PlotRange -> {{0.5, 2}, {-0.25, 0.9}}]

It should be noted that these two guesses do not have to bracket the root. We have called the two initial guesses in the way which we have because that will be the format for subsequent iterations. It does not matter which guess is which. Try switching the two initial guesses to see what happens. One should converge faster than the other.

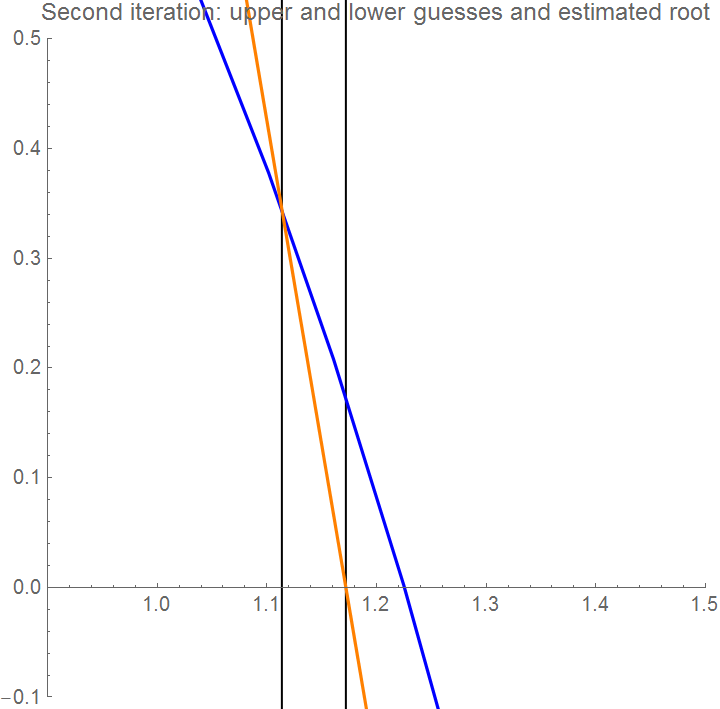
We make the second iteration.

x2 = x1 - (f[x1]*(xguess2 - x1))/(f[xguess2] - f[x1])

1.17199

Then we plot bounds.

m = (f[x1] - f[xguess2])/(x1 - xguess2);
secantline[x_] = m*x + f[x1] - m*x1;
sline = Plot[secantline[x], {x, 1, 1.3}, PlotStyle -> {Orange}]
Show[Graphics[Line[{{xguess2, maxi}, {xguess2, mini}}]],
Graphics[Line[{{x1, maxi}, {x1, mini}}]], curve,
Graphics[Line[{{xguess1, maxi}, {xguess1, mini}}]], sline,
Axes -> True, PlotLabel -> "Function with upper and lower guesses and estimated root",
PlotStyle -> {FontSize -> 10}, PlotRange -> {{0.5, 2}, {-0.25, 0.9}}]

Third iteration gives.

x3=x2-(f[x2]*(x1-x2))/(f[x1]-f[x2])

1.23113

   ■

It is possible to combine the secant method and weighed Newton's method:

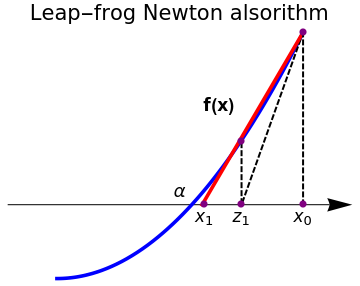
		plot = Plot[1*x^2, {x, 0, 1}, AspectRatio -> 1, PlotStyle -> {Thickness[0.01], Blue}, Axes -> False, Epilog -> {PointSize[0.03], Pink, Point[{{0, 0}, {2, 2.8}}]}, PlotRange -> {{-0.5, 1.2}, {-0.2, 1.4}}]; arrow = Graphics[{Arrowheads[0.07], Arrow[{{-0.2, 0.3}, {1.2, 0.3}}]}]; l1 = Graphics[{Thick, Dashed, Line[{{1, 1}, {0.75, 0.3}}]}]; l2 = Graphics[{Thickness[0.01], Red, Line[{{1, 1}, {0.59, 0.3}}]}]; l3 = Graphics[{Thick, Dashed, Line[{{1, 1}, {1, 0.3}}]}]; l4 = Graphics[{Thick, Dashed, Line[{{0.75, 0.55}, {0.75, 0.3}}]}]; t2 = Graphics[{Black, Text[Style[Subscript[x, 0], 16], {1, 0.25}]}]; t3 = Graphics[{Black, Text[Style[Subscript[z, 1], 16], {0.75, 0.25}]}]; t4 = Graphics[{Black, Text[Style[Subscript[x, 1], 16], {0.6, 0.25}]}]; t5 = Graphics[{Black, Text[Style[\[Alpha], 16], {0.5, 0.35}]}]; t9 = Graphics[{Black, Text[Style["f(x)", Bold, 16], {0.66, 0.7}]}]; Show[arrow, plot, l1, l2, l3, l4, t2, t3, t4, t5, t9, Epilog -> {PointSize[0.02], Purple, Point[{{0.6, 0.3}, {0.75, 0.555}, {0.75, 0.3}, {1, 0.3}, {1, 1}}]}, PlotLabel -> "Leap-frog Newton alsorithm", LabelStyle->{FontSize->16,Black} ]
Leap-frog Newton's algorithm.		Mathematica code

Example 10: Consider the Chebyshev polynomial of the first kind that is the solution of the initial value problem

\[ \left( 1 - x^2 \right) y'' -x\,y' + n^2 y = 0, \qquad y(0) = \begin{cases} 1, & \ \mbox{ for } \ n = 4k, \\ -1 , & \ \mbox{ for } \ n = 4k + 2, \\ 0, & \ \mbox{ for } n = 2k+1, \end{cases} \]

These polynomials are denoted by T_n(x):

\[ T_n (x) = \begin{cases} \cos \left( n\,\mbox{arccos}\,x \right) , & \ \mbox{ if } \ |x| ≤ 1, \\ \cosh \left( n\,\mbox{arccosh}\,x \right) , & \ \mbox{ if } \ x ≥ 1, \\ (-1)^n \cosh \left( n\,\mbox{arccosh}\,(-x) \right) , & \ \mbox{ if } \ x ≤ -1 . \end{cases} \]

We choose n = 12 and plot the chebyshev polynomial T₁₂(x).

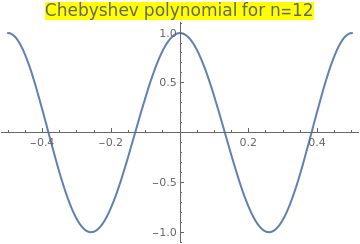
		Plot[ChebyshevT[12, x], {x, -0.5, 0.5}, PlotStyle -> Thick, PlotLabel -> Style["Chebyshev polynomial for n=12", FontSize -> 16, Background -> Yellow]] Then we write the code based on leap-frog Newton algorithm f[x_] = ChebyshevT[12, x]; f1[x_] = D[f[x], x]; RecurrenceTable[{x[k + 1] == x[k] - (z[k] - x[k])*f[x[k]]/(f[z[k]] - f[x[k]]), z[k + 1] == x[k] - f[x[k]]/f1[x[k]], x[0] == 0.1, z[0] == 0.1 - f[0.1]/f1[0.1]}, {x, z}, {k, 0, 5}]// Grid {{0.1, 0.132044}, {0.13049, 0.132044}, {0.130526, 0.130526}, {0.130526, 0.130526}, {0.130526, 0.130526}, {0.130526, 0.130526}} ListPlot[%, PlotRange -> All]
Chebyshev polynomial of the first kind.		Mathematica code

So we see that three iterations are need to obtain six digit accuracy root: 0.130526.    ■

Suppose that we need to find a root α of a smooth function f, so f(α) = 0. Given an adequate starting value x₀, a sequence of values x₁, x₂, … , x_n, … can be generated using the Steffensen's formula below

Johan's revolutionary idea is based on applying Newton's iteration scheme but replacing the derivative in (Newton.1) by the forward approximation:    \( \displaystyle f' \left( x_k \right) \approx \frac{f \left( x_k + f( x_k )\right) - f \left( x_k \right)}{ f \left( x_k \right)} = \frac{f\left( x_k + h \right) - f\left( x_k \right)}{h} ,\) where h = f(x_k) plays the role of the infinitesimal increment, which is close to zero when x_k is near the root α. Now it is clear why Steffensen's method is very sentitive to the initial quess value x₀ because f(x₀) must be very small. However, a more accurate approximation is obtained by utilizing a symmetric difference quotient

Note that only the head of the function is specified when it is passed to the SteffensonMethod subroutine. Steffensen's algorithm can be implemented within the Wolfram language with the aid of NestWhileList command. The nesting iteration will be terminated when the last two iterates become the same, but no more than 20 times (by default n ≤ 20):

Although Steffensen's method works very well, because of machine limitations, there could be situations when the denominator may lose significant places due to subtraction of two almost equal floating point terms. To avoid such situations, Steffensen's algorithm can be modified with either Aitken's delta-squared process or introducing a real parameter p:

Example 11: Consider the Chebyshev polynomial of the second kind that is the polynomial solution of the initial value problem

\[ \left( 1 - x^2 \right) y'' -3x\,y' + n \left( n +2 \right) y = 0, \qquad y(0) = \begin{cases} \phantom{-}1, & \ \mbox{ for } \ n = 4k, \\ -1 , & \ \mbox{ for } \ n = 4k + 2, \\ \phantom{-}0, & \ \mbox{ for } n = 2k+1, \end{cases} \]

These polynomials are denoted by U_n(x):

\[ U_n (x) = \frac{\sin \left( (2n+1)\,\mbox{arccos} x \right)}{\sin \left( \mbox{arccos} x \right)} , \qquad n=0,1,2,\ldots . \]

We choose n = 11 and plot the chebyshev polynomial U₁₁(x).

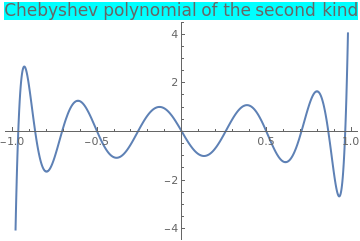
		Plot[ChebyshevU[11, x], {x, -1, 1}, PlotStyle -> Thick, PlotLabel -> Style["Chebyshev polynomial of the second kind", FontSize -> 16, Background -> Cyan]]
Chebyshev polynomial of the second kind.		Mathematica code

First, we bracket a positive root of the Chebyshev polynomial:

N[ChebyshevU[11, 1/10]]

-0.937464

N[ChebyshevU[11, 1/3]]

0.854319

So we know that a positive zero of U₁₁(x) is somewhere in the interval [0.1, 0.33]. Then we find its root with the standard Mathematica command:

FindRoot[ChebyshevU[11, x], {x, 0.3}]

{x -> 0.25881904510252074}

We make a few steps manually to see how Steffensen's algorithm works. With an initial approximation x₀ = 0.3, we get

f[x_] = ChebyshevU[11, x]; a = 0.3; p0=f[a];
x1 = a - p0^2/(ChebyshevU[11, a + p0] - p0)

0.0426704

Since the values of the function U₂₂(0.3) = 0.516061 and U₂₂(0.1) = -0.937464 at the endpoints cannot be considered as «infinitesimal», we expect Steffensen's method to diverge. We make the second step and obtain

p0 = ChebyshevU[11, x2]; p02 = p0^2; x3 = x2 - p02/(ChebyshevU[11, x2 + p0] - p0 - 6*p02)

1.04959

So we see that if we go far away from the root, Steffensen's method diverges. If we use a symmetric version (Steffensen.2), the algorithm also diverges, but slowly.

f[x_] = ChebyshevU[11, x]; a = 0.1;
i = 1; NN = 30; tol = 1/10^7; p0 = N[f[a]]; p02 = p0*p0; x0 = a;
While[i < NN,
x1 = x0 - 2*p02/(f[x0 + p0] - f[x0 - p0]);
x0 = x1; p0 = N[f[x0]]; p02 = (f[x0])^2;
Print["i= ", i, ", x= ", x1, ", f= ", p0]; i++]

Instead of the classical algorithm (Steffensen.1), we consider a modified one (Steffensen.3), with p = 6.

On the first step, we get

x1 = 0.1 - p0^2/(ChebyshevU[11, 0.1 + p0] - p0 - 6*p0^2)

0.261254

The second step gives

p0=ChebyshevU[11, x1]; p02=p0^2;
x2 = x1 - p02/(ChebyshevU[11, x1 + p0] - p0 - 6*p02)

0.25874

The third step yields

p0=ChebyshevU[11, x2]; p02=p0^2;
x3 = x2 - p02/(ChebyshevU[11, x2 + p0] - p0 - 6*p02)

0.258819

Since we get eight correct decimal places, there is no need for further iteration and we claim that three iterations with the modified Steffensen's method is sufficed to obtain the root of the equation U₁₁(x = 0.

We write a loop:

f[x_] = ChebyshevU[11, x]; a = 0.1;
i = 1; NN = 5; tol = 1/10^7; p0 = N[f[a]]; p02=p0*p0; x0 = a;
While[i < NN,
x1 = x0 - p02/(f[x0 + p0] - p0 - 6*p02);
x0 = x1; p0 = N[f[x0]]; p02 = (f[x0])^2;
Print["i= ", i, ", x= ", x1, ", f= ", p0]; i++
]

Next, we check the Steffensen-secant algorithm (Steffensen.4) with p = 6:

f[x_] = ChebyshevU[11, x]; a = 0.1;
i = 1; NN = 5; tol = 1/10^7; p0 = N[f[a]]; p02=p0*p0; x0 = a;
While[i <= NN,
z1 = x0 - p02/(f[x0 + p0] - p0 - 6*p02);
x1=x0 - (z1-x0)*p0/(f[z1]-p0);
x0 = x1; p0 = N[f[x0]]; p02 = (f[x0])^2;
Print["i= ", i, ", x= ", x1, ", f= ", p0]; i++
]

So we get the correct 6 decimal places on the second step. However, with p = 0, Steffensen-secant algorithm diverges because the secant line becomes horizontal.

We compare our results with Newton's method (Newton.1):

NewtonsMethodList[ChebyshevU[11, x], {x, 0.1}, 5]

{0.1, -0.109996, 0.2054, 0.26945, 0.258806, 0.258819}

Hence, we see that Newton's method makes five iterations to achieve the required accuracy.

Now we investigate the sensitivity of Steffensen's algorithm to the starting value. Utilizing ListLinePlot facilitates to see how quickly the solution stabilizes. The dashed thick red line shows the solution as determined by Mathematica built-in command FindRoot.

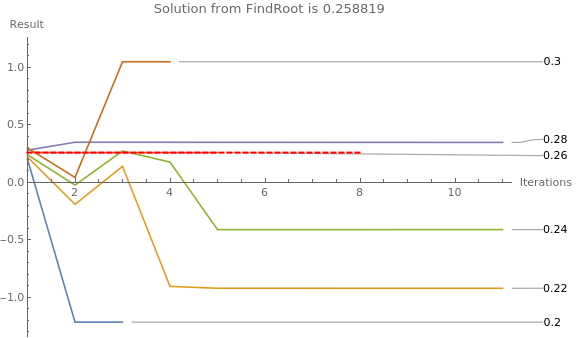
		(* making a list of some starting values *) x0List = Range[0.2, 0.3, 0.02] {0.2, 0.22, 0.24, 0.26, 0.28, 0.3} Then we map the function across the list of starting values. The maximum number of iterations is 10 simply for aesthetic purposes. root = FindRoot[f[x], {x, 0.3}]; ListLinePlot[ SteffensonMethod2[f, #, 10] & /@ x0List, (* the root determined by FindRoot is shown as a thick red dashed line *) Epilog -> {Thick, Dashed, Red, Line[{{1, x}, {8, x}}] /. root}, (* Adding labels, legends, making the plot look nicer *) PlotLabels -> x0List, ImageSize -> Large, AxesLabel -> {"Iterations", "Result"}, PlotRange -> {{1, Automatic}, Automatic}, PlotLegends -> x0List, PlotLabel -> "Solution from FindRoot is " <> ToString[x /. root] ]
Sensitivity of Steffensen's algorithm to the starting value.		Mathematica code

   ■

Example 13: Let us find a root of the Laguerre polynomial L₂₁(x) of order 21 that can be defined by the Rodrigues formula

\[ L_n (x) = \frac{e^x}{n!}\,\frac{{\text d}^n}{{\text d} x^n} \left( e^{-x} x^n \right) = \frac{1}{n!} \left( \frac{\text d}{{\text d}x} - 1 \right)^n x^n , \qquad n=0,1,2,\ldots . \]

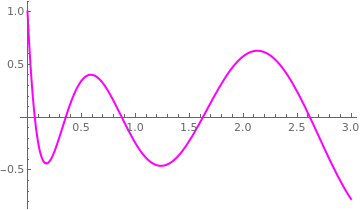
		We plot the Laguerre polynomial to identify the interval containing the root. Plot[LaguerreL[21, x], {x, 0, 3}, PlotStyle -> {Thick, Magenta}]
Graph of the Laguerre polynomial L21(x).		Mathematica code

Since these polynomials were discovered by P.Chebyshev, they are called also Chebyshev--Laguaere polynomials, after Edmond Laguerre (1834–1886).

To find its first positive root, we use the standard Mathematica command

FindRoot[LaguerreL[21, x], {x, 0}]

{x -> 0.0672578}

Now we apply the Chebyshev iterative procedure:

N[ChebyshevMethodList[LaguerreL[21, x], {x, 0}, 3]]

{0., 0.0589569, 0.0672194, 0.0672578}

and with three iterations, we obtain the correct answer with 10 decimal places. However, with Newton's method,

N[NewtonsMethodList[LaguerreL[21, x], {x, 0}, 4]]

{0., 0.047619, 0.0649839, 0.0672227, 0.0672578}

we obtain 9 correct decimal places with four iterations.    ■

There is another version of the preceding algorithm that is of order 3 and it is called the super-Halley:

Example 15: Let us find a root of the Legendre polynomial P₂₀(x) of order 20 that can be defined by the Rodrigues formula

\[ P_n (x) = \frac{1}{2^n n!} \,\frac{{\text d}^n}{{\text d} x^n} \left( x^2 - 1 \right)^n , \qquad n=0,1,2,\ldots . \]

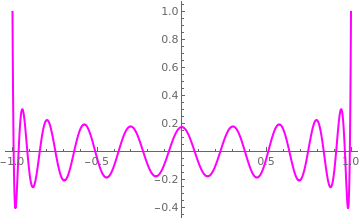
		Legendre polynomials are named after Adrien-Marie Legendre (1752--1833), who discovered them in 1782. We plot the Legendre polynomial to identify the interval containing the root. Plot[LegendreP[20, x], {x, 0, 3}, PlotStyle -> {Thick, Magenta}]
Graph of the Legendre polynomial P20(x).		Mathematica code

First, we find the third positive zero of the Legendre polynomial with the aid of Mathematica standard command

FindRoot[LegendreP[20, x], {x, 0.2}]

{x -> 0.227786}

Then we apply the Halley method

N[HalleyMethodList[LegendreP[20, x], {x, 0.2}, 3]]

{0.2, 0.225813, 0.227785, 0.227786}

So three iterations is enough to get the correct answer with 16 correct decimal places. To obtain the same accuracy, it requires four iterations with Newton's method. On the other hand, super-Halley scheme gives only 15 correct decimal places with 3 iterations.    ■

As we saw previously, combination of different iteration algorithms may lead to acceleration of convergence or make it more robust. It was a Dutch mathematician, called Theodorus Jozef Dekker (born in 1927), who proposed an algorithm in 1960 to combine the open iterative method (not restricted to an interval, but usually converges quickly without any guarantee of finding a root) and the closed iterative method (that uses a bounded interval and usually converges slowly to a root if it exists). In particular, he suggested to alternate the robust bisection method (which is slow in computations) with the fast open end secant iterative algorithm. Unfortunately, his original paper is not available on the web, but his next paper published with J.Bus in 1975 can be seen on the Internet. Theodorus Jozef Dekker completed his Ph.D degree from the University of Amsterdam in 1958. Later, Dekker's method was modified, and its latest version, known as Brent or van Wijngaarden--Dekker--Brent method is discussed in the next subsection. Our presentation provides a rough outline of the basic algorithm and does not include possible improvements.

The advantages of Dekker's method were outlined by the founder of the computer science department at Stanford university George E. Forzythe (who was a Ph.D adviser of Cleve Moler, an inventor of matlab):

• it is as good as the bisection method, so it always converges to the root;
• there are no assumptions about the second derivative of the function;
• it is as fast as the secant method;
• it is not concerned with multiple roots unlike the secant method.

Suppose that we want to solve the equation f(x) = 0, where f:  ℝ → ℝ is a smooth real-valued function. As with the bisection method, we need to initialize Dekker's method with two points, say 𝑎₀ and b₀, such that \( f \left( a_0 \right) \quad\mbox{and} \quad f \left( b_0 \right) \) have opposite signs. If f is continuous on \( \left[ a_0 , b_0 \right] , \) the intermediate value theorem guarantees the existence of a solution between a₀ and b₀.

The Algorithm

Two points are involved in every iteration: 𝑎 and b, where b is the current guess for the root α of f(x).

• Dekker's method starts with two points that embrace a root α, for which f(α) = 0. So there exists an interval that includes the root:    α ∈ [𝑎, b], with f(𝑎) × f(b) < 0.
• 𝑎_k is the "contrapoint," i.e., a point such that \( f \left( a_k \right) \quad\mbox{and} \quad f \left( b_k \right) \) have opposite signs, so the interval \( \left[ a_k , b_k \right] \) contains the solution. Furthermore, \( \left\vert f \left( b_k \right) \right\vert \) should be less than or equal to \( \left\vert f \left( a_k \right) \right\vert , \) so that b_k is a better guess for the unknown solution than 𝑎_k.
• At every step of iteration, the following conditions are maintained:
  \[ f\left( a_k \right) \times f\left( b_k \right) \le 0, \quad \left\vert f\left( b_k \right) \right\vert \le \left\vert f\left( a_k \right) \right\vert , \quad \left\vert a_k - b_k \right\vert \le 2\,\delta (b) , \]
  where δ is the required tolerance.
• b_k-1 is the previous iterate (for the first iteration, we set b_k-1 = 𝑎₀).
• Calculate two values: one using the secant method
  \[ s = b_k - \frac{b_k - b_{k-1}}{f\left( b_k \right) - f\left( b_{k-1} \right)}\, f\left( b_k \right) , \qquad \mbox{if } f\left( b_k \right) \ne f\left( b_{k-1} \right) , \]
  and another midpoint
  \[ m = \frac{f(a_k ) + f(b_k )}{2} \qquad \mbox{if } f\left( b_k \right) = f\left( b_{k-1} \right) . \]
• If the value s from the secant algorithm lies strictly between b_k and m, then it becomes the next iterate: b_k+1 = s.
• Otherwise, b_k+1 = m.
• The new contrapoint is chosen such that f(𝑎_k+1) and f(b_k+1) have opposite signs. If f(𝑎_k) and f(b_k+1) have opposite signs, then the contrapoint remains the same: 𝑎_k+1 = 𝑎_k. Otherwise, f(b_k+1) and f(b_k) have opposite signs, so the new contrapoint becomes 𝑎_k+1 = b_k.
• Finally, if |f(𝑎_k+1)| < |f(b_k+1)|, then 𝑎_k+1 is probably a better guess for the required zero than b_k+1, and hence the values of 𝑎_k+1 and b_k+1 are swapped.

Example 17: Use the Bus--Dekker method to find a root of the equation

\[ e^{0.1\,x} - e^{0.7\,x -1} = 0 \]

in the interval [1,3]. First, we plot the given function f

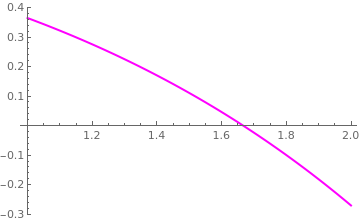
		Plot[Exp[0.1*x]-Exp[0.7*x-1], {x,1,2}, PlotStyle->{Thick, Magenta}]
Figure 1: Jordan region for m > 0.		Mathematica code

We observe that f(1) is positive while f(2) is negative, and hence that there is at least one root in [1,2]. The basis of the Bus--Dekker algorithm is to use the secant method but at the same time ensure a reduction of an interval containing a zero. We start with guesses x = 0 and x = 1.5. Since f(1.5) is positive, we can immediately reduce the interval containing a zero from the initial interval [1,2] to [1.5,2]. So we set b₁ = 1.5 and 𝑎 = 2.

f[x_] = Exp[0.1*x] - Exp[0.7*x - 1];
b=1.5; a=2;
m = (a+b)/2

1.75

and secant value:

s = (a*f[b] - b*f[a])/(f[b] - f[a])

1.6451

Comparison of the values of the function at these two points

f[m]

-0.0610765

f[s]

0.0151544

reveals that these points bracket the root. So we set for the second iteration b₂ = s = 1.6451 and 𝑎 = m = 1.75. Next iteration gives

b = s; a = m;
m = (a+b)/2

1.69755

and secant value:

s = (a*f[b] - b*f[a])/(f[b] - f[a])

1.66596

Then we evaluate the values at these points:

f[s]

0.000504238

f[m]

-0.0221636

Since these two points embrace the root, we set b₃ = s = 1.66596 and 𝑎 = m = 1.69755. The third iteration gives

b = s; a = m;
m = (a+b)/2

1.68175

and secant value:

s = (a*f[b] - b*f[a])/(f[b] - f[a])

1.66666

So with the three iterations, we get six correct decimal places of the root:

FindRoot[f[x], {x, 0.6}]

1.6666666666666667

   ■

Dekker's method performs well if the function f is reasonably well-behaved. However, there are circumstances in which every iteration employs the secant method, but the iterates b_k converge very slowly (in particular, \( \left\vert b_k - b_{k-1} \right\vert \) may be arbitrarily small). Dekker's method requires far more iterations than the bisection method in this case. Although this algorithm guarantees the convergence and the asymptotic behavior is completely satisfactory, the number of function evaluations required by this algorithm may be prohibitively large, in particular, when the zero appears to be multiple one.

In 1971, the Australian mathematician Richard Pierce Brent (born in 1946, Melbourne) proposed a modification of Dekker's method. With the additional inclusion of the inverse quadratic interpolation, Brent's root-finding algorithm makes it completely robust and usually very efficient. The method is the basis of matlab’s fzero routine (see its explanation on Cleve’s Corner). The algorithm tries to use the potentially fast-converging secant method or inverse quadratic interpolation if possible, but it falls back to the more robust bisection method if necessary. The method underwent several modifications, improvements, and implementations. Consequently, the algorithm is also known as the van Wijngaarden-Deker-Brent method.

For Brent's original algorithm, the upper bound of the number of function evaluations needed equals (t + 1)² - 2, where t is the number of function evaluations needed by bisection. Later, J.C.P. Bus & T.J. Dekker proposed another modification of Brent's algorithm, but requiring at most 4t function evaluations. This is achieved by inserting steps in which rational interpolation or bisection is performed. Some other variations of Brent's method are known with a similar asymptotic behavior. Our presentation outlines the basic ideas and does not follow any version of Brent's algorithm. The example presented illustrates the Brent's method by showing all steps.

The inverse quadratic interpolation method approximates the function y = f(x) by a quadratic curve that goes through three consecutive points { x_i, f(x_i) }, i = (k, k-1, k-2). As the function may be better approximated by a quadratic curve rather than a straight line, the iteration is likely to converge more quickly. Such a quadratic approximation follows:

The Algorithm

Three points are involved in every iteration: 𝑎, b, and c, where b is the current guess for the root α of f(x). Since there are many checks at every iteration step, we give only basical ideas involved in Brent's algorithm.

• Brent's method starts with two points that embrace a root α, for which f(α) = 0. So there exists an interval that includes the root:    α ∈ [b, c], with f((b) × f(c) < 0.
• Initiation: out of two endpoints that embrace the root α, set b to be that which gives the the smallest function value:    |f(b)| ≤ |f(c)|.
• Set 𝑎 = c and determine a new iterate b by linear (secant) interpolation
  \[ b= b_1 = \frac{a\,f(b) - b\,f(a)}{f(b) - f(a)} . \]
  Then set c to be the previous value of b if the function f changes the sign. If not, swap with 𝑎.
• If the three current points 𝑎, b, and c are distinct, find another point i by inverse quadratic interpolation.
• If it fails, try to compute a secant intercept s using b and c. Test whether s is between b and (3𝑎+b)/4. Otherwise set s = m, the midpoint.
• Since b is the most recent approximation to the root and 𝑎 is the previous value of b, apply the linear interpolation if |f(b)| ≥ |f(𝑎)|. Otherwise, do bisection.
• Make a new estimate of the root using the obtained points through either the bisection, secant, or IQI methods, and set b to that closest to the root. Use bisection when when the condition |s - b| < 0.5 |b - c| fails.
Check for convergence at the new calculated value. If reached, end the algorithm.
• Check whether f(new value) and f(b) have different signs. If so, they will be the two estimates for the next iteration. If not, the values would be 𝑎 and the newly calculated value.
Refresh values of points so that abs(f(b)) < abs(f(𝑎)).
• Start next iteration.

Brent's method contains many comparisons and conditions that make it complicated to follow. It has various implementations; for instance, Bus & Dekker suggest to insert the bisection method at every 5-th iterate. A great deal of attention has been paid to considerations of floating-point arithmetic (overflow and underflow, accuracy of computed expressions, etc.). Let us outline the main check-in points.

Two inequalities must be simultaneously satisfied: Given a specific numerical tolerance δ if the previous step used the bisection method, the inequality

If the previous step performed interpolation, then the inequality

Also, if the previous step used the bisection method, the inequality

Brent proved that his method requires at most N² iterations, where N denotes the number of iterations for the bisection method. If the function f is well-behaved, then Brent's method will usually proceed by either inverse quadratic or linear interpolation, in which case it will converge superlinearly.

Furthermore, Brent's method uses inverse quadratic interpolation (IQI for short) instead of linear interpolation (as used by the secant method). If \( f(b_k ), \ f(a_k ) , \mbox{ and } f(b_{k-1}) \) are distinct, it slightly increases the efficiency. As a consequence, the condition for accepting i (the value proposed by either linear interpolation or inverse quadratic interpolation) has to be changed: s has to lie between \( \left( 3 a_k + b_k \right) /4 \) and b_k.

Example 18: Consider the Airy function f(-x) = Ai(-x) of the first kind for negative argument:

\[ \mbox{Ai}(-x) = \frac{1}{\pi} \int_0^{\infty} \cos \left( \frac{t^3}{3} - xt \right) {\text d} t = \frac{1}{\pi} \sqrt{\frac{-x}{3}} \,K_{1/3} \left( \frac{2}{3} \,(-x)^{3/2} \right) , \]

where K_ν(z) is the modified Bessel function of second kind or Macdonald function. We first plot this function.

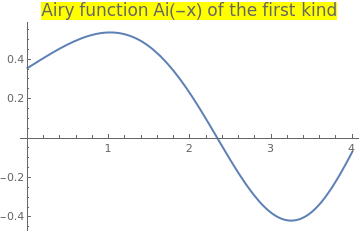
		Plot[AiryAi[-x], {x, 0, 4}, PlotStyle -> Thick, PlotLabel -> Style["Airy function Ai(-x) of the first kind", FontSize -> 16, Background -> Yellow]]
Airy function Ai(-x) of the first kind.		Mathematica code

First, we find the root using the standard Mathematica command

FindRoot[AiryAi[-x], {x, 2}]

{x -> 2.33811}

From the graph of the Airy function, we identify the first root belongs to the interval [1, 3]. Upon calculating the values of the function at these endpoints, we set b = 3 and c = 𝑎 = 1.

f[x_] = AiryAi[-x];
N[f[1]]

0.535561

N[f[3]]

-0.378814

In the first iteration, we use linear interpolation between (1, 0.535561) and (3, -0.378814), which yields i = 2.17142.

b = (N[f[3]] - 3*f[1])/(f[3] - f[1])

2.17142

The value of the function at this point is

b2=f[b]

0.115663

In the second iteration, we use inverse quadratic interpolation (IQI) between three points

\[ (a,f(a)) = (1,0.535561), \quad (b, f(b)) = (2.17142, 0.115663), \quad (c,f(c)) = (3,-0.378814) . \]

a = 1; c = 3;
A = f[b]*f[c]*a/(a - b)/(a - c) + f[a]*f[c]*b/(b - a)/(b2 - c) + f[a]*f[b]*c/(c - a)/(c - b2)

0.180425

Since

f[A]

0.401355

is larger than f(b), we use the bisection method.

m=(b+c)/2; f[m]

-0.169288

So we bracket the root with points b = 2.17142 and c = 2.58571, with f(c) = -0.169288. Then we use the IQI and set

a=3; b=2.17142; c=m;
A = f[b]*f[c]*a/(a - b)/(a - c) + f[a]*f[c]*b/(b - a)/(b2 - c) + f[a]*f[b]*c/(c - a)/(c - b2)

0.00762649

Since

f[%]

0.441646

we use linear interpolation with b = 2.17142 and c = 2.58571:

b = (N[f[3]] - 3*f[1])/(f[3] - f[1]); c=2.58571;
s = (c*f[b] - b*f[c])/(f[b] - f[c])

2.33959

Since

f[s]

-0.00103677

is negative, we set b = s = 2.33959, c = 2.17142, and 𝑎 = 2.58571. Then with the aid of IQI, we determine the the approximate

a= 2.58571; b = 2.33959; c=(N[f[3]] - 3*f[1])/(f[3] - f[1]);
A = f[b]*f[c]*a/(a - b)/(a - c) + f[a]*f[c]*b/(b - a)/(b - c) + f[a]*f[b]*c/(c - a)/(c - b)

1.10925

Since

f[%]

0.533359

exceeds the previous f(b) = 0.00103961, we use again the linear approximation

s= (c*f[b]-b*f[c])/(f[b]-f[c])

2.33809

with

f[s]

0.0000108358

positive, and f(2.33959) negative, we know that these two points embrace the root. Using linear approximation, we get

b= 2.33809; c=2.33959; s= (c*f[b]-b*f[c])/(f[b]-f[c])

2.33811

Since

f[s]

-9.18718*10^-12

we claim that the root is α = 2.33811, which is obtained on the fourth iteration.    ■

Alexander Markowich Ostrowski (1893---1986) was a talented Russian mathematician who was gifted with a phenomenal memory. Alexander was born to Jewish family in Kiev, Russian Empire. Alexander Ostrowski attended the Kiev College of Commerce, not a high school, and thus had an insufficient qualification to be admitted to university. However, his talent did not remain undetected: Ostrowski's mentor, professor at the University of Kiev, Dmitry Grave, wrote to German mathematicians Edmund Landau (1877--1938) and Kurt Hensel (1861--1941) for help. Subsequently, Ostrowski began to study mathematics at Marburg University in Germany under Hensel's supervision in 1912. When World War I broke out, he was therefore interned as a hostile foreigner. During this period, he was able to obtain limited access to the university library. After the war he resumed his studies at the more prestigious University of Göttingen and was awarded a doctorate in mathematics in 1920. He graduated summa cum laude and worked in different universities. He eventually moved to Switzerland to teach at the University of Basel, before the outbreak of World War II. Ostrowski fared well living in that neutral country during the war. He taught in Basel until he retired in 1958. He remained very active in math until late in his life.

This gifted and prolific mathematician was engaged in various mathematical problems. The advent of computers catapulted Ostrowski to delve into numerical analysis. He studied iterative solutions of large linear systems. Ostrowski passed away in 1986 in Montagnola, Lugano, Switzerland. He had lived there with his wife during his retirement.

Ostrowski tackled the problem of calculating a root for a single-variable non-linear function in a new way. Most of the methods we know perform a single refinement, for the guess of the root, in each iteration. Ostrowski’s novel approach was to obtain an interim refinement for the root and then further enhance it by the end of each iteration. The two-step iterations in Ostrowski’s method use the following two equations:

\[ \begin{split} y_{n} &= x_n - f(x_n )/f' (x_n ) , \\ x_{n+1} &= y_n - \frac{f(y_n ) \left( x_n - y_n \right)}{\left( f(x_n ) - 2\,f(y_n ) \right)} = x_n - \frac{f\left( x_n \right)}{f' \left( x_n \right)} \cdot \frac{f\left( x_n \right) - f\left( y_n \right)}{f\left( x_n \right) - 2\,f\left( y_n \right)} , \end{split} \qquad n=0,1,2,\ldots . \tag{Ostrowski.1} \]

The first equation for y_n applies the basic Newton algorithm as the first step to calculate y_n which Ostrowski uses as an interim refinement for the root. The iteration’s additional refinement for the root comes by applying the latter equation. Ostrowski’s algorithm has a fourth-order convergence, compared to Newton’s algorithm which has a second-order convergence. This is an optimal method by the Kung-Traub conjecture. Thus, Ostrowski’s method converges to a root faster than Newton’s method. There is the extra cost of evaluating an additional "function call" to calculate f(yn) in Ostrowski’s method. This extra cost is well worth it, since, in general, the total number of function calls for Ostrowski’s method is less than that for Newton’s method.

Ostrowski’s method has recently inspired quite a number of new algorithms that speed up convergence. These algorithms calculate two and even three interim root refinements in each iteration. While these methods succeed in reducing the number of iterations, they fail to consistently reduce the total number of function calls, compared to the basic Ostrowski’s method. For example, the second equation can be chosen as

\[ x_{n+1} = y_n - \frac{\delta \left( y_n - x_n \right) f(y_n )}{f(y_n ) - \gamma\,f(x_n )} \]

for some real numbers δ and γ. In particular, if δ = γ = 1, we get the Newton-Secant method. Taking δ = γ = 1/2 leads to the well-known Ostrowski's method. For example, if we apply Newton's method again, we obtain the eighth order three-step iterative method with five function evaluations:

\begin{align*} y_{n} &= x_n - \frac{f(x_n )}{f' (x_n )} , \\ z_n &= x_n - \frac{f\left( x_n \right)}{f' \left( x_n \right)} \cdot \frac{f\left( x_n \right) - f\left( y_n \right)}{f\left( x_n \right) - 2\,f\left( y_n \right)} , \tag{Ostrowski.2} \\ x_{n+1} &= z_n - \frac{f(z_n )}{f' (z_n )} , \qquad n=0,1,2,\ldots . \end{align*}

Example 19: Roots of Jacobi elliptic function

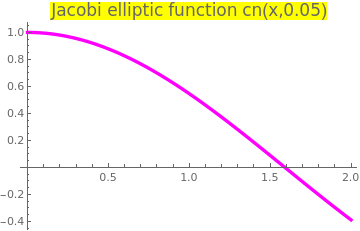
Example 19: Let us consider the Jacobi elliptic cosine function cn(x, k), which is a solution of the boundary value problem

\[ \frac{{\text d}^2 y}{{\text d} x^2} = \left( 2 - k^2 \right) y - 2\,y^3 , \qquad y(0,k) = y(K(k)) = 0, \]

where

\[ K(k) = \int_0^1 \frac{{\text d}t}{\sqrt{\left( 1 - t^2 \right) \left( 1 - k^2t^2 \right)}} = \int_0^{\pi/2} \frac{{\text d}\theta}{\sqrt{1 - k^2 \sin^2 \theta}} \]

is the complete elliptic integral. The Jacobi elliptic cosine function can also be defined implicitly:

\[ \mbox{cn}(u,k) = \cos \phi , \qquad u = \int_0^{\phi} \frac{{\text d}\theta}{\sqrt{1 - k^2 \sin^2 \theta}} \qquad 0 < k < 1. \]

The parameter k is referred to as the elliptic modulus of u and ϕ, which we set k = 0.05.

		Upon plotting the elliptic cosine function we determine an interval [1,2] containing its zero. Plot[JacobiCN[x, 1/20], {x, 0, 2}, PlotStyle -> {Thickness[0.01], Magenta}, PlotLabel -> Style["Jacobi elliptic function cn(x,0.05)", FontSize -> 16, Background -> Yellow]]
Jacobi elliptic cosine function cn(-x,0.05).		Mathematica code

First, we find its root using the standard Mathematica command

FindRoot[JacobiCN[x, 1/20], {x, 2}]

1.5910034537907924

Since we want to apply Ostrowski's method, we need the derivative of the elliptic cosine function:

D[JacobiCN[x, 1/20], x]

-JacobiDN[x, 1/20] JacobiSN[x, 1/20]

\[ \frac{{\text d}\,{\mbox cn}(x,k)}{{\text d}x} = - \mbox{sn}(x,k)\,{\mbox dn}(x,k) . \]

We choose an initial guess point to be x₀ = 1 and find the first iterate.

f[x_] = JacobiCN[x, 1/20];
f1[x_] = D[JacobiCN[x, 1/20], x];

Newton's approximation is

y1=1.0-f[1.0]/f1[1.0]

1.6635 + 0. I

Then the first value becomes

x1 = 1.0 -f[1.0]/f1[1.0]*(f[1.0]-f[y1])/(f[1.0]-2*f[y1])

1.59533 + 0. I

For the second iterate, we have

y2=x1-f[x1]/f1[x1]

1.591 + 0. I

and

x2 = x1 -f[x1]/f1[x1]*(f[x1]-f[y2])/(f[x1]-2*f[y2])

1.5910034537907236 +0. I

So we use only two iterations, which allows to obtain 14 correct decimal places!

If we apply the Chebyshev iteration scheme, we need four iterations to obtain the same accuracy:

f[x_] = JacobiCN[x, 1.0/20];
ChebyshevMethodList[f[x], {x, 1}, 4]
Re[%]

{1, 1.5277, 1.59097, 1.591, 1.591}

On the other hand, Newton's method requires five iterations:

NewtonsMethodList[f[x], {x, 1.0}, 5]
Re[%]

{1., 1.6635, 1.59089, 1.591, 1.591, 1.591}

   ■

• Gautschi, Walter, "Alexander M. Ostrowski (1893–1986): His life, work, and students", can be downloaded from http://www.cs.purdue.edu/homes/wxg/AMOengl.pdf.
• Grau-Sánchez, M., Grau, A., Noguera, M., "Ostrowski type methods for solving systems of nonlinear equations," Applied Mathematics and Computation, 2011, Vol. 218, pp. 2377–2385.
• Shammas, N., Ostrowski’s Method for Finding Roots

 

 

IX. Muller’s Method

---

Muller’s method is a generalization of the secant method, in the sense that it does not require the derivative of the function. Muller's method finds a root of the equation \( f(x) =0 . \) It is an iterative method that requires three starting points \( \left( p_0 , f(p_0 ) \right) , \ \left( p_1 , f(p_1 ) \right) , \ \left( p_2 , f(p_2 ) \right) . \) A parabola is constructed that passes through the three points; then the quadratic formula is used to find a root of the quadratic for the next approximation. If the equation f(x) = 0 has a simple root, then it has been proved that Muller’s method converges faster than the secant method and almost as fast as Newton’s method. The method can be used to find real or complex zeros of a function and can be programmed to use complex arithmetic.

David Eugene Muller (1924--2008) was a professor of mathematics and computer science at the University of Illinois (1953–1992), when he became an emeritus professor, and was an adjunct professor of mathematics at the New Mexico State University (1995-2008). Muller received his BS in 1947 and his PhD in 1951 in physics from Caltech; an honorary PhD was conferred by the University of Paris in 1989. He was the inventor of the Muller C-element (or Muller C-gate), a device used to implement asynchronous circuitry in electronic computers. He also co-invented the Reed–Muller codes.

Without loss of generality, we assume that p₂ is the best approximation to the root and consider the parabola through the three starting values. Make the change of variable

\[ t= x- p_2 , \]

and use the differences

\[ h_0 = p_0 - p_2 , \qquad h_1 = p_1 - p_2 . \]

Consider the quadratic polynomial involving the variable t:

\[ y = at^2 +bt +c \]

that passes through these three initial points:

\begin{align*} \mbox{at } t&= h_0: \qquad ah_0^2 +bh_0 +c = f_0 = f(h_0 ) , \\ \mbox{at } t&= h_1: \qquad ah_1^2 +bh_1 +c = f_1 = f(h_1 ) , \\ \mbox{at } t&= 0: \qquad a0^2 +b0 +c = f_2 = f(0 ) , \\ \end{align*}

Solving these three equations, we find

\[ a= \frac{\left( f_0 -c \right) h_1 - \left( f_1 -c \right) h_0}{h_1 h_0^2 - h_1^2 h_0} , \qquad b = \frac{\left( f_1 -c \right) h_0^2 - \left( f_0 -c \right) h_1^2}{h_1 h_0^2 - h_1^2 h_0} , \qquad c= f_2 . \]

The quadratic formula is used to find the roots \( t = z_1 , \ z_2 \) of the equation \( at^2 + bt +c =0 : \)

\[ z = \frac{-2c}{b \pm \sqrt{b^2 - 4ac}} . \]

To update the iterates, throw out the one of the initial points that is farthest away. Although a lot of auxiliary calculations are done in Muller’s method, it only requires one function evaluation per iteration.

If Muller’s method is used to find the real roots of \( f(x) =0 , \) it is possible that one may encounter complex approximations, because the roots of the quadratic in \( at^2 + bt +c =0 \) might be complex (nonzero imaginary components). In these cases the imaginary components will have a small magnitude and can be set equal to zero so that the calculations proceed with real numbers.

Example 20: Bernoulli polynomial

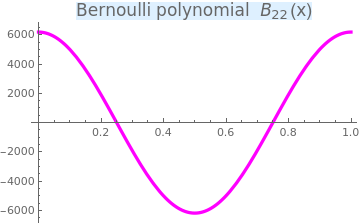
Example 20: We consider the Bernoulli polynomial of order n:

\[ B_n (x) = \sum_{k=0}^n \binom{n}{k} B_k x^{n-k} = \frac{{\texttt D}}{e^{\texttt D} -1} \, x^n , \]

where

\[ B_k = \sum_{i=0}^k \frac{1}{i+1} \sum_{j=0}^i (-1)^j \binom{i}{j} j^k \]

is the Bernoulli number.

		Upon plotting the Bernoulli polynomial we determine an interval [0.1, 0.5] containing its zero. Plot[{BernoulliB[22, x]}, {x, 0, 1}, PlotStyle -> {Thickness[0.01], Magenta}, PlotLabel -> Style["Bernoulli polynomial \!\(\*SubscriptBox[\(B\), \ \(22\)]\)(x)", FontSize -> 16, Background -> LightBlue]]
Bernoulli polynomial of order 22.		Mathematica code

First, we pick up three points (x₁, y₁), (x₂, y₂), and (x₃, y₃), where

\[ x_1 = 0.1, \quad x_2 = 0.3, \quad x_3 = 0.5, \qquad y_i = B_{22} \left( x_i \right) , \quad i =1,2,3. \]

So y1 = 5009.53, y2 = -1913.47, and y3 = -6192.12. Then the next iterate x₄ is a solution of the quadratic equation

\[ a\,x^2 + b\, x + c = 0 , \]

where

\begin{align*} a &= \frac{\left( y_1 - y_2 \right) - \left( y_2 - y_3 \right)\left( x_1 - x_2 \right) / \left( x_2 - x_3 \right)}{x_1^2 - x_2^2 - \left( x_2^2 - x_3^2 \right) \left( x_1 - x_2 \right) / \left( x_2 - x_3 \right)} = 33054.4, \\ b &= \frac{\left( y_1 0 y_2 \right) - a \left( x_1^2 - x_2^2 \right)}{x_1 - x_2} = -47836.8, \\ c &= y_1^2 - a\,x_1^2 - b\,x_1 = 9462.67 . \end{align*}

x1 = 0.1; x2 = 0.3; x3 = 0.5; y1 = BernoulliB[22, x1]; y2 = BernoulliB[22, x2]; y3 = BernoulliB[22, x3]; a = (y1-y2 -(y2-y3)*(x1-x2)/(x2-x3))/(x1^2 - x2^2 -(x2^2 - x3^2)*(x1-x2)/(x2-x3)); b = (y1-y2 -a*(x1^2 -x2^2))/(x1-x2); c = y1-a*x1^2 -b*x1;

root = FindRoot[a*x^2 + b*x + c , {x, 0.1}] x4 = x /. root

0.23644

We remove the largest value (x₁, y₁) and set instead our new value. So we set x₁ = 0.23644. Now we can pproceed with the next iteration.

\begin{align*} a &= \frac{\left( y_1 - y_2 \right) - \left( y_2 - y_3 \right)\left( x_1 - x_2 \right) / \left( x_2 - x_3 \right)}{x_1^2 - x_2^2 - \left( x_2^2 - x_3^2 \right) \left( x_1 - x_2 \right) / \left( x_2 - x_3 \right)} = 64509.1, \\ b &= \frac{\left( y_1 0 y_2 \right) - a \left( x_1^2 - x_2^2 \right)}{x_1 - x_2} = -73000.5 \\ c &= y_1^2 - a\,x_1^2 - b\,x_1 = 14180.9 . \end{align*}

x1 = x4; y1 = BernoulliB[22, x4]; a = (y1-y2 -(y2-y3)*(x1-x2)/(x2-x3))/(x1^2 - x2^2 -(x2^2 - x3^2)*(x1-x2)/(x2-x3)); b = (y1-y2 -a*(x1^2 -x2^2))/(x1-x2); c = y1-a*x1^2 -b*x1;

root = FindRoot[a*x^2 + b*x + c , {x, 0.1}] x4 = x /. root

0.249082

The value of the Bernoulli polynomial at this point is

BernoulliB[22, x4]

35.7025

which is too llarge. therefore, we need to make the third iteration and pick x4 as x3:

x3 = x4; y3 = BernoulliB[22, x4]; a = (y1-y2 -(y2-y3)*(x1-x2)/(x2-x3))/(x1^2 - x2^2 -(x2^2 - x3^2)*(x1-x2)/(x2-x3)); b = (y1-y2 -a*(x1^2 -x2^2))/(x1-x2); c = y1-a*x1^2 -b*x1;

root = FindRoot[a*x^2 + b*x + c , {x, 0.1}] x4 = x /. root

0.249082

which is closed to the true answer provided by Mathematica:

FindRoot[BernoulliB[22, x], {x, 0.1}]

0.25

   ■

 

References

1. Brent, R.P., An algorithm with guaranteed convergence for finding a zero of a function, Computer Journal, 1971, Vol. 14, Issue 4, pp. 422-425.
2. Bus, J. C. P., and T. J. Dekker, Two efficient algorithms with guaranteed convergence for finding a zero of a function, ACM Transactions on Mathematical Software (TOMS), 1.4 (1975): 330-345.
3. Chun, C., Ham, Y.M., Some fourth-order modifications of Newton’s method, Applied Mathematics and Computation, 2008, Vol. 197, pp. 654--658.
4. Dekker, T.J., Finding a zero by means of successive linear interpolation, Constructive Aspects of the Fundamental Theorem of Algebra, B. Dejon and P. Henrici, Eds., Wiley Interscience, London, 1969, pp. 37--51.
5. Feng, X.L., He, Y.N., High order iterative methods without derivatives for solving nonlinear equations, Applied Mathematics and Computation, 2007, Vol. 186, pp. 1617--1623.
6. Jarratt, P., Some fourth order multipoint iterative methods for solving equations, Math. Comput. 20 (95) (1966) 434–437.
7. King, R.F., A Family of Fourth Order Methods for Nonlinear Equations, SIAM Journal on Numerical Analysis, 1973, Volume 10, Issue 5, pp. 876--879. https://doi.org/10.1137/0710072
8. Kou, J., Li, Y., The improvements of Chebyshev–Halley methods with fifth-order convergence, Applied Mathematics and Computation, 2007, Volume 188, Issue 1, pp. 143--147. https://doi.org/10.1016/j.amc.2006.09.097
9. Kung, H.T., Traub, J.F., Optimal order of one-point and multipoint iteration, Journal of the Association for Computing Machinery (ACM), 1974, Vol. 21, No. 4, pp. 643--651. https://doi.org/10.1145/321850.321860
10. Muller, D.E., A method for solving algebraic equations using automatic computer, Mathematical Tables and other Aids to Computation, 1956, Vol. 10, No. 56, pp. 208--215.
11. Ostrowski, A.M., Solution of Equations in Euclidean and Banach Space, Academic Press, New York, 1973.
12. Parhi, S.K., Gupta, D.K., A sixth order method for nonlinear equations, Applied Mathematics and Computation, 2008, Vol. 203, pp. 50--55.
13. Traub. J.F., Iterative Methods for the Solution of Equation, American Mathematical Society; Second Edition (January 1, 1982) New Jersy.
14. Wang, X., Kou, J., Li, Y., A variant of Jarratt method with sixth-order convergence, Applied Mathematics and Computation, 2008, Vol. 204, pp. 14--19.

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)