Preface
This tutorial was made solely for the purpose of education and it was designed for students taking Applied Math 0330. It is primarily for students who have very little experience or have never used Mathematica and programming before and would like to learn more of the basics for this computer algebra system. As a friendly reminder, don't forget to clear variables in use and/or the kernel. The Mathematica commands in this tutorial are all written in bold black font, while Mathematica output is in normal font.
Finally, you can copy and paste all commands into your Mathematica notebook, change the parameters, and run them because the tutorial is under the terms of the GNU General Public License (GPL). You, as the user, are free to use the scripts for your needs to learn the Mathematica program, and have the right to distribute this tutorial and refer to this tutorial as long as this tutorial is accredited appropriately. The tutorial accompanies the textbook Applied Differential Equations. The Primary Course by Vladimir Dobrushkin, CRC Press, 2015; http://www.crcpress.com/product/isbn/9781439851043
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to the main page for the second course APMA0340
Return to the main page for the first course APMA0330
Return to Part III of the course APMA0330
Glossary
Milne--Simpson Method
Another popular predictor-corrector scheme is known as the Milne or Milne--Simpson method. See
Milne, W. E., Numerical Solutions of Differential Equations, Wiley, New York, 1953.
Its predictor is based on integration of the slope function f(t, y(t)) over the interval \( \left[ x_{n-3} , x_{n+1} \right] \) and then applying the Simpson rule:
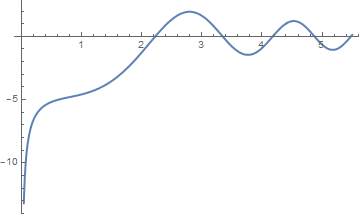
Example. Let us start with the Riccati equation \( y' = x^2 + y^2 \) subject to the initial condition \( y(0) =-1 . \) Its solution is expressed through Bessel functions:
Plot[d[x], {x, 0, 5.5}, PlotStyle -> Thick]
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Pr