Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to Part V of the course APMA0330

Glossary

Famous Curves

 

Antiversiera

For two values of parameters:
a=-2; b=1;
and
a = 1; b = 2;
we have two graphs:

ContourPlot[ x^4 - 2*a*x^3 + 4*a^2/b^2*y^2 == 0, {x, -5, 2}, {y, -2, 2}, AspectRatio -> Automatic]

            

 

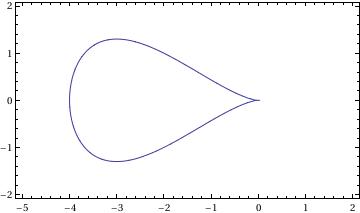
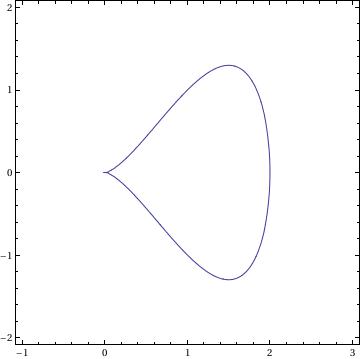
Arachnida

a = 1; n = 3;
PolarPlot[ 2*a*Sin[n*\[Phi]]/Sin[(n - 1)*\[Phi]], {\[Phi], .0001, 2*\[Pi]}]

 

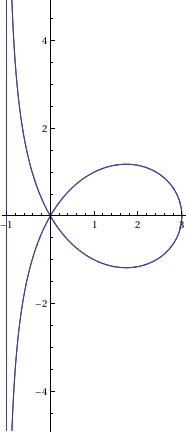
Astroid

t = {1, 2, 3, 4};
ContourPlot[(x^2 + y^2 - t^2)^3 + 27*x^2*y^2 == 0, {x, -5, 5}, {y, -5, 5}]
or
ContourPlot[x^(2/3) + y^(2/3) = 1, {x,-1,1},{y,-1,1}]

 

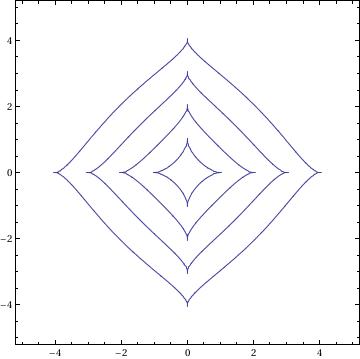
Besace

a = {1, 2, 3}; b = {1, 2, 3};
ContourPlot[(x^2 - b*y)^2 + a^2*(y^2 - x^2) == 0, {x, -5, 5}, {y, -1.5, 4.5}, AspectRatio -> Automatic]


 

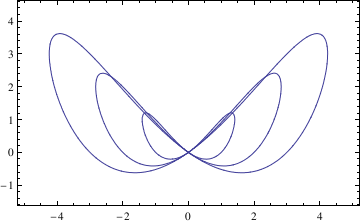
Bifolium

b = {0, 1, 2, 3};
ContourPlot[(x^2 + y^2)^2 == b*x^2*y, {x, -1, 1}, {y, -0.2, 1}, AspectRatio -> Automatic]

 

 

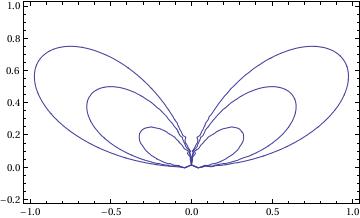
Cardioid

r = {1, 2, 3};
PolarPlot[2*r*(1 - Cos[\[Phi]]), {\[Phi], 0, 2*\[Pi]}, AspectRatio -> Automatic]

 

 

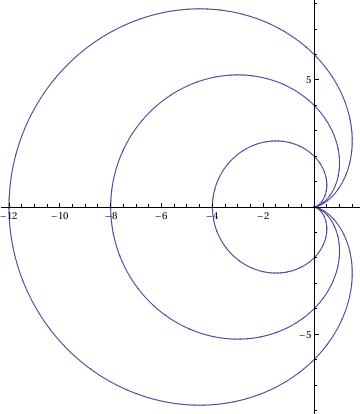
Circular Tractrix

a:=1;
f[r_, th_] := th - ArcTan[Sqrt[4*a^2 - r^2]/r] - Sqrt[4*a^2 - r^2]/r
g[r_, th_] := {r Cos[th], r Sin[th]}
pl = ContourPlot[f[r, th] == 0, {r, 0, 8 Pi}, {th, 0, 4 Pi}, PlotPoints -> 30];
pl[[1, 1]] = g @@@ pl[[1, 1]];
Show[pl, PlotRange -> All, AspectRatio -> 1.5/2]

 

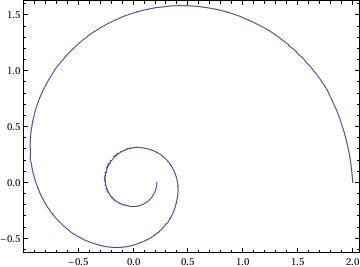
Cramer

r=2;l=1;
ContourPlot[ x*(x^2 + y^2) == (r + l)*x^2 - (r - l)*y^2, {x, -1, 5}, {y, -5, 5}, AspectRatio -> 1]

 

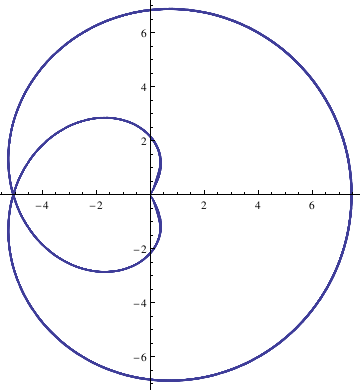
Epicycloid

R = 1; h = 5; r = 2;
PolarPlot[Sqrt[ R^2 + h^2 - 2*(R + r)*h*Cos[R/r*\[Phi]]], {\[Phi], 0, 200*\[Pi]}]

 

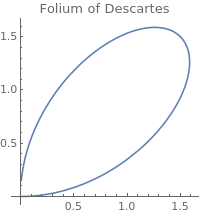
Folium of Descartes

Clear[f, g, t]; f[t_] = 3 t/(1 + t^3);
g[t_] = 3 t^2 /(1 + t^3);
ParametricPlot[{f[t], g[t]}, {t, 0, 20}, PlotRange ->All, AspectRatio -> 1, Plotlabel -> "Folium of Descartes", ImageSize ->200]

 

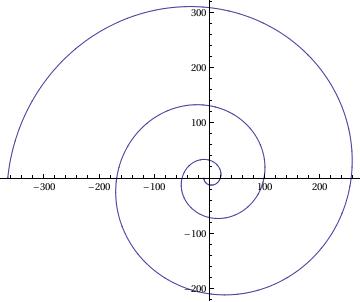
Galileo's Spiral

a=-1;l=10;
PolarPlot[a*\[Phi]^2 - l, {\[Phi], 0, 6*\[Pi]}]

 

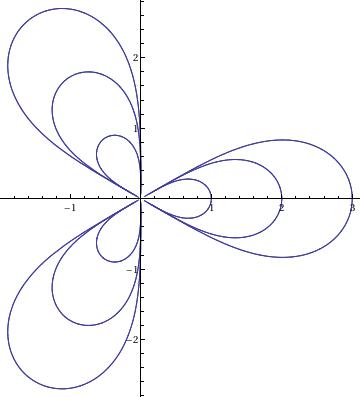
Kiepert

    Kiepert curves
l = {1, 2, 3};
PolarPlot[(l^3*Cos[3*\[Phi]])^(1/3), {\[Phi], -2*\[Pi], 2*\[Pi]}

 

Lemniscate

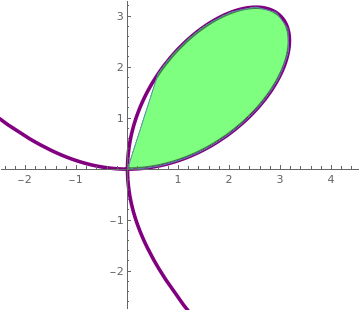
A lemniscate is any of several figure-eight or ∞-shaped curves. The word comes from the Latin "lēmniscātus" meaning "decorated with ribbons", from the Greek λημνίσκος meaning "ribbons", or which alternatively may refer to the wool from which the ribbons were made.
    Lemniscate
F[t_] := 6*(Sec[t] Tan[t])/(1 +Tan[t]^3)
lemniscate = PolarPlot[F[t], {t,-Pi/6, 3*Pi/4.2}, PlotStyle -> {{Purple, Thickness[0.01]}}] ;
shadingRight = ParametricPlot[{F[t]}, {t,0,CubeRoot[2]}, {r,0,F[t]}, PlotStyle -> {Red, Opacity[0.5]}, Mesh->None];
shadingLeft = ParametricPlot[{r*Cos[t], r*Sin[t]}, {t,0,CubeRoot[2]}, {r,0,F[t]}, PlotStyle -> {Green, Opacity[0.5]}, Mesh->None];
Show[lemniscate,shadingRight,shadingLeft]
 

Limaçon

Limaçon
A limaçon or limacon, also known as a limaçon of Pascal, is defined as a roulette formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp. Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart-shaped, or it may be oval.
    Limaçon
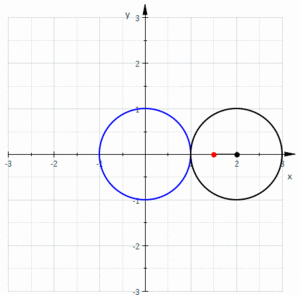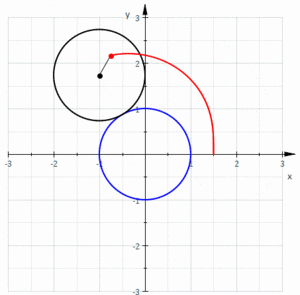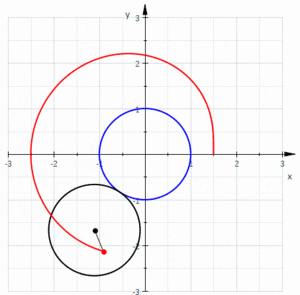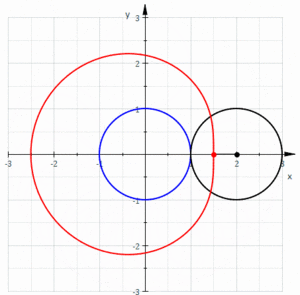
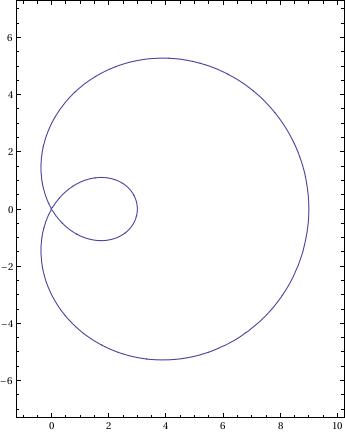
a=3; l=3;
ContourPlot[(x^2 + y^2 - 2*a*x)^2 == l^2*(x^2 + y^2), {x, -1,
10}, {y, -7, 7}, AspectRatio -> 14/11]
w

 

Rose

k=3;
PolarPlot[a*Cos[k*\[Phi]], {\[Phi], 0, 4*\[Pi]}]

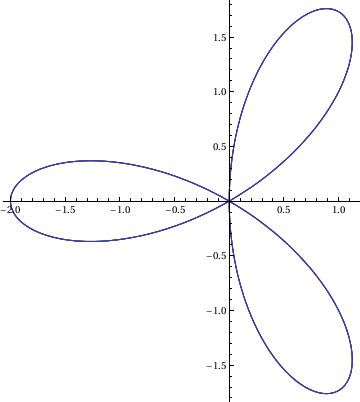
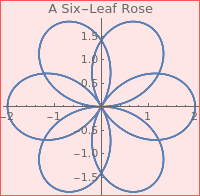
PolarPlot[2 Cos[3*theta/2], {theta, -4*Pi, 4*Pi}, PlotLabel ->"A Six-Leaf Rose", AspectRatio ->Automatics, ImageSize->200]

 

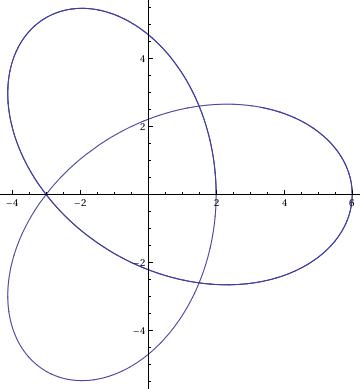
Trefoil

r=2;
ParametricPlot[{r*(2*Cos[2*t] - Cos[t]), r*(2*Sin[2*t] + Sin[t])}, {t, 0, 10}]


 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)