Preface
When an initial value problem has a solution that cannot be obtained from the general solution by choosing an appropriate value of an arbitrary constant, then such solution is called the singular solution. In this case the initial value problem has multiple solutions and uniqueness fails.
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the third course APMA0360
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Return to Part II of the course APMA0330
Glossary
Singular Solutions
Consider a first order differential equation
\begin{equation}
F\left( x, y , y' \right) =0, \qquad \mbox{where} \quad y' = {\text d}y/{\text d}x = {\texttt D}y
\label{Eq.singular.1}
\end{equation}
is the derivative of the function y(x) with respect to independent variable x. If the function F is smooth, then Eq.\eqref{Eq.singular.1} can be solved with respect to y' according to the inverse function theorem; this leads to the differential equation in the normal form:
\begin{equation}
y' = f(x,y) .
\label{Eq.singular.2}
\end{equation}
Solving Eq.\eqref{Eq.singular.1} is equivalent to determination of the null-space (also called kernel) of the operator F. Generally speaking, F is an operator because it
assigns to every input function y(x) the output F(x, y, y'),
involving a derivative operator \( \texttt{D} = {\text d}/{\text d}x . \) Solving Eq.\eqref{Eq.singular.1} means determination of all functions y(x) that are annihilated by the operator F(x, y, y'). You know from calculus that \( \texttt{D} \) is an unbounded operator and its null-space is a one dimensional space spanned on a constant function: \( \texttt{D}^{-1} \,f(x) = \int f(x) \,{\text d} x + c . \) Note that D-1 is not a true inverse, but only the right inverse: \( \texttt{D}\,\texttt{D}^{-1} = I , \quad \texttt{D}^{-1} \texttt{D} \ne I, \) where I is the identical operator.
Therefore, it is expected that the null-space of F is also a one-dimensional space depending on some constant. If this is true, the null-space is called the general solution in the opposite to calculus where the term «antiderivative» is used. A general solution of Eq.\eqref{Eq.singular.1} or \eqref{Eq.singular.2} depends on a constant and is usually written as a relation
\begin{equation}
\psi (x, y, c ) = 0 ,
\label{Eq.singular.3}
\end{equation}
where c is an arbitrary constant from some domain. Equation \eqref{Eq.singular.3} defines a one-parameter family of solutions to the equation F(x, y, y') = 0. However, for some equations, the null-space of F(x, y, y') = 0 is more complicated and may contain functions that are not included into the general form \eqref{Eq.singular.3}; such solutions deserve a special attention.
The differential equation \eqref{Eq.singular.1} may have solutions that cannot be obtain from
ψ(x, y, c) = 0 for an appropriate choice of a constant c.
A solution is
called the singular solution of the differential equation F(x, y, y') = 0 if it cannot be obtained from the general solution for any choice of arbitrary constant c, including infinity, and for which the initial value problem has failed to have a unique solution.
Therefore, the null-space of the differential operator \eqref{Eq.singular.1} may consist of two parts: solutions that are determined by the relation \eqref{Eq.singular.3} (called the general solution) and those that are not identified by Eq.\eqref{Eq.singular.3}. The latter comprises the set of singular solutions. Uniqueness theorems, presented in section, show the cases when singular solutions do not exist. For example, if a slope function in Eq.\eqref{Eq.singular.2} is a Lipschitz function in variable y, then a singular solution does not exist. You will learn later that linear equations as well and Bernoulli equations have no a singular solution.
Obviously, an initial value problem with multiple solutions may be not suitable for modeling because it confuses a software in use. In applications, when uniqueness of solutions is required, singular solutions must be eliminated.
One of the common ways to determine existence of a singular solution is to eliminate c from the system of equations:
\[
\psi \left( x, y, c \right) =0 , \qquad \frac{\partial \psi}{\partial c} = 0.
\]
A singular solution in a stronger sense is such function that is
tangent to every solution from a family of solutions, forming the envelope of this family of solutions.
Constant functions are usually not solutions of the differential equations unless they annihilate the slope function. In this case, we call them critical points or equilibrium/stationary solutions. Therefore, if y = y* vanishes the slope function, \( f(x, y^{\ast} ) \equiv 0 , \) then y = y* is the equilibrium solution of the differential equation \( y' = f(x, y ) . \) A stationary solution may be singular or not, which we will show in the following examples.
Example 1:
Consider Clairaut's equation
y=xy' + (y')^2
y=xy' + (y')^2
Clear[y];
y[x_] = x c + c^2
samples =Table[y[x],{c,-3,3,1/4}]
Plot[Evaluate[samples],{x,-3,3},PlotRange->{-5,5}]
y[x_] = x c + c^2
samples =Table[y[x],{c,-3,3,1/4}]
Plot[Evaluate[samples],{x,-3,3},PlotRange->{-5,5}]
Out[18]= c^2 + c x
Out[19]= {9 - 3 x, 121/16 - (11 x)/4, 25/4 - (5 x)/2, 81/16 - (9 x)/4, 4 - 2 x,
49/16 - (7 x)/4, 9/4 - (3 x)/2, 25/16 - (5 x)/4, 1 - x,
9/16 - (3 x)/4, 1/4 - x/2, 1/16 - x/4, 0, 1/16 + x/4, 1/4 + x/2,
9/16 + (3 x)/4, 1 + x, 25/16 + (5 x)/4, 9/4 + (3 x)/2,
49/16 + (7 x)/4, 4 + 2 x, 81/16 + (9 x)/4, 25/4 + (5 x)/2, 121/16 + (11 x)/4, 9 + 3 x}
Out[20]=
Out[19]= {9 - 3 x, 121/16 - (11 x)/4, 25/4 - (5 x)/2, 81/16 - (9 x)/4, 4 - 2 x,
49/16 - (7 x)/4, 9/4 - (3 x)/2, 25/16 - (5 x)/4, 1 - x,
9/16 - (3 x)/4, 1/4 - x/2, 1/16 - x/4, 0, 1/16 + x/4, 1/4 + x/2,
9/16 + (3 x)/4, 1 + x, 25/16 + (5 x)/4, 9/4 + (3 x)/2,
49/16 + (7 x)/4, 4 + 2 x, 81/16 + (9 x)/4, 25/4 + (5 x)/2, 121/16 + (11 x)/4, 9 + 3 x}
Out[20]=
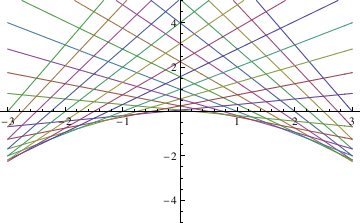
To find the singular solution (envelope), we type:
f[t_] = t^2;
Eliminate[{x==-f'[t],y==f[t]-t*f'[t]},t]
Eliminate[{x==-f'[t],y==f[t]-t*f'[t]},t]
Out[37]= -4y==x^2
■
End of Example 1
Example 2:
Consider the Clairaut equation
■
\[
y' \left( x\,y' -3\,y \right) + 2 = 0 ,
\]
which has the general solution \( c^2 x - 3c\,y + 2 =0 ,
\) c ≠ 0. Differentiating with respect to c, we get
\[
2cx - 2y =0 \qquad \Longrightarrow \qquad c = y/x .
\]
Substituting this value into the general equation formula, we obtain the
singular solution:
\[
x \left( \frac{y}{x} \right)^2 - 3\, \frac{y^2}{x} + 2 =0 \qquad
\Longrightarrow \qquad y^2 = x.
\]
|
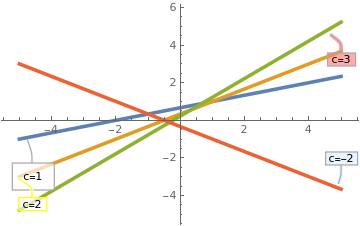
Now we plot some representatives from the general solution.
Plot[{Callout[(x + 2)/3, "c=1", Above, Frame -> True,
FrameMargins -> 10],
Callout[(4*x + 2)/6, "c=2", Below, Frame -> True,
CalloutStyle -> Yellow],
Callout[(9*x + 2)/9, "c=3", Right, Frame -> True,
Background -> Pink],
Callout[(4*x + 2)/(-6), "c=-2", Right, Frame -> True,
Background -> LightBlue]}, {x, -5, 5},
PlotStyle -> Thickness[0.01]]
|
|
| The family of solutions. | Mathematica code |
■
End of Example 2
Example 3:
Consider the autonomous equation
One of these curves from the primitive F(x, y, y') = 0 can be chosen to satisfy the initial condition y(x0) = y0:
The equilibrium solution y = 1 is a singular envelope for the family of general solutions. ■
\[
\frac{{\text d}y}{{\text d}x} = \sqrt{1-y^2} \qquad (y^2 \le 1).
\]
Separation of variables and integration yields
\[
\frac{{\text d}y}{\sqrt{1-y^2}} = {\text d}x
\Longrightarrow \qquad \arcsin y = x + c ,
\]
where c is a constant of integration. For y ∈ [-1, 1], we apply sine function and obtain
|
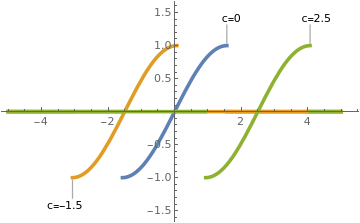
y1[x_] = Piecewise[{{0, x < -Pi/2}, {Sin[x], -Pi/2 <= x <= Pi/2}, {0,
x > Pi/2}}];
y2[x_] = Piecewise[{{0, x < -Pi/2 - 1.5}, {Sin[x + 1.5], -Pi - 1.5/2 <= x <= Pi/2 - 1.5}, {0, x > Pi/2 - 1.5}}]; y3[x_] = Piecewise[{{0, x < -Pi/2 + 2.5}, {Sin[x - 2.5], -Pi + 2.5/2 <= x <= Pi/2 + 2.5}, {0, x > Pi/2 + 2.5}}]; Plot[{Callout[y1[x], "c=0", Above], Callout[y2[x], "c=-1.5", Below], Callout[y3[x], "c=2.5", Above]}, {x, -5, 5}, PlotStyle -> Thickness[0.01]] |
|
| Three members of the general solution. | Mathematica code |
One of these curves from the primitive F(x, y, y') = 0 can be chosen to satisfy the initial condition y(x0) = y0:
\[
x - x_0 = \arcsin y - \arcsin y_0 \qquad -1 \le y \le 1 , \quad -1 - \arcsin y_0 \le x - x_0 \le 1 - \arcsin y_0 .
\]
However, the given initial value problem:
\[
y' = \sqrt{1-y^2} , \qquad y\left( x_0 \right) = 1
\]
has a singular solution:
\[
y(x) = \begin{cases}
1, & \ \mbox{ for } x > x_0 , \\
\cos \left( x - x_0 \right) , & \ \mbox{ for } x_0 - \pi < x < x_0 , \\
-1 , & \ \mbox{ for } x < x_0 - \pi .
\end{cases}
\]
|
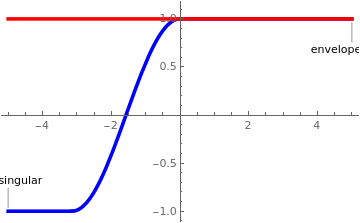
Now we plot the singular solution (in blue) along with the singular envelope (in red).
s[x_] = Piecewise[{{1, x > 0}, {Cos[x], -Pi <= x <= 0}, {-1,
x < -Pi}}];
env[x_] = 1; Plot[{Callout[s[x], "singular", Left], Callout[env[x], "envelope", Right]}, {x, -5, 5}, PlotStyle -> {{Blue, Thickness[0.01]}, {Red, Thickness[0.01]}}] |
|
| Singular solution and the envelope. | Mathematica code |
The equilibrium solution y = 1 is a singular envelope for the family of general solutions. ■
End of Example 3
Example 4:
Consider the initial value problem
■
\[
\frac{{\text d}y}{{\text d}x} = \begin{cases}
\frac{4 x^3 y}{x^4 + y^2}, & \ \mbox{ if } x \ne 0 \quad\mbox{or}\quad y \ne 0,
\\
0, & \ \mbox{ if } x=y=0 .
\end{cases} \qquad y(0) = 0.
\]
It is easy to show that the slope function, which we denote by f(x, y), is a continuous function in two variables x and y. On the other hand,
\[
\left\vert f(x, y_1 ) - f(x, y_2 ) \right\vert = \left\vert \frac{4 x^3 y_1}{x^4 + y^2_1} - \frac{4 x^3 y_2}{x^4 + y^2_2} \right\vert = \frac{4 x^3 \left( x^4 - y_1 y_2 \right)}{\left( x^4 + y_1^2 \right)\left( x^4 + y_2^2 \right)} \left( y_2 - y_1 \right) .
\]
If y1 = p x² and y2 = q x², then
\[
\left\vert f(x, y_1 ) - f(x, y_2 ) \right\vert = 4\left\vert \frac{1-pq}{\left( 1 + p^2 \right)\left( 1 + q^2 \right)} \right\vert \left\vert \frac{y_2 - y_1}{x} \right\vert .
\]
Therefore, the Lipschitz condition is not satisfied throughout any region containing the origin.
The given equation admits the explicit solution
\[
y = c^2 - \sqrt{x^4 + c^2} ,
\]
containing an arbitrary real constant c. Since this function satisfies the initial condition y(0) = 0, the given initial value problem has infinite many solutions.
|
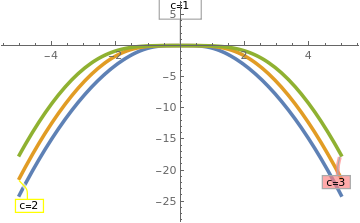
Now we plot several singular solutions.
Plot[{Callout[(x + 2)/3, "c=1", Left, Frame -> True,
FrameMargins -> 10],
Callout[(4*x + 2)/6, "c=2", Below, Frame -> True,
CalloutStyle -> Yellow],
Callout[(9*x + 2)/9, "c=3", Right, Frame -> True,
Background -> Pink],
Callout[(4*x + 2)/(-6), "c=-2", Right, Frame -> True,
Background -> LightBlue]}, {x, -5, 5},
PlotStyle -> Thickness[0.01]]
|
|
| Three singular solutions. | Mathematica code |
■
End of Example 4
- Show that y′ = yp, where p is a constant such that 0 < p < 1 has the trivial solution y = 0 and \( \displaystyle \quad y = \left[ \left( 1-p \right) \left( x+c \right) \right]^{1/(1-p)} . \)
- Find the general solution of dy/dx = y³. Is y = 0 a singular solution?
- Coddington, E.A. and Levinson, N., Theory of Ordinary Differential Equations, McGraw-Hill; 1st edition, 1984.
- Dobrushkin, V.A., Applied Differential Equations: The Primary Course, Second edition, CRC Press, Boca Raton, FL, 2021.
- Hale, J.K., Ordinary Differential Equations (Dover Books on Mathematics), Illustrated Edition, 2009.
- Ince, E.L., Ordinary Differential Equations (Dover Books on Mathematics) Illustrated Edition, 1956.
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)