Preface

This section shows Mathematica capabilities to plot figures in polar coordinates.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Return to Part I of the course APMA0330

Glossary

Polar Plots

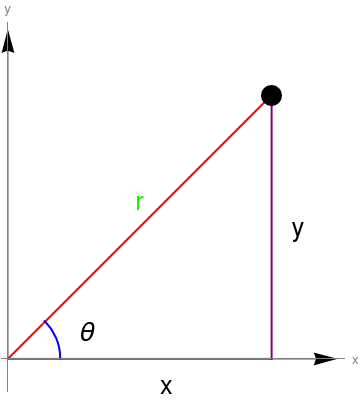
We use polar coordinates as an alternative way to describe points in the plane. In polar coordinates, we describe points via their angle (called argument or polar angle) with the positive x-axis measured in counterclockwise direction, and the distance from the origin (called radial distance). See figure below.

point = Graphics[[Black, Disk[{1,1}, 0.04]}];
liner = Graphics[{Red, Thick, Line[{{0, 0}, {1, 1}}]}];
r = Graphics[Text[Style["r", Large, Green], {0.5, 0.6}]];
linex = Graphics[{Orange, Thick, Line[{{0, 0}, {1, 0}}]}];
x = Graphics[Text[Style["x", Large, Black], {0.6, -0.1}]];
y = Graphics[Text[Style["y", Large, Black], {1.1, 0.5}]];
liney = Graphics[{Purple, Thick, Line[{{1, 0}, {1, 1}}]}];
theta = Graphics[Text[Style["\[Theta]", Large, Black], {0.3, 0.1}]];
arc = Graphics[{Blue, Thick, Circle[{0, 0}, 0.2, {0, Pi/4}]}];
arrowx = Graphics[{Arrowheads[0.07], Arrow[{{0, 0}, {1.25, 0}}]}];
arrowy = Graphics[{Arrowheads[0.07], Arrow[{{0, 0}, {0, 1.25}}]}];
Show[{liner, r, linex, x, liney, y, arc, theta, point, arrowx, arrowy}, Ticks -> None, Axes -> True, AxesStyle -> Gray, AxesLabel -> {Style["x", Medium, Gray], Style["y", Medium, Gray]}]
From this picture, it should be clear that we can switch back and forth between the Cartesian coordinate system and polar coordinate system in the following manner:
\[ x= r\,\cos \theta , \qquad y = r\,\sin \theta , \]
and
\[ r = \sqrt{x^2 + y^2} \ge 0, \qquad \theta = \begin{cases} \arctan \left( \frac{y}{x} \right) , & \ \mbox{ if } \ x > 0 , \\ \arctan \left( \frac{y}{x} \right) + \pi , & \ \mbox{ if } \ x < 0 \mbox{ and } \ y\ge 0, \\ \arctan \left( \frac{y}{x} \right) - \pi , & \ \mbox{ if } \ x < 0 \mbox{ and } \ y< 0, \\ \frac{\pi}{2} , & \ \mbox{ if } \ x=0 \mbox{ and } \ y> 0, \\ -\frac{\pi}{2} , & \ \mbox{ if } \ x=0 \mbox{ and } \ y< 0, \\ \mbox{undefined} & \ \mbox{ if } \ x=0 \mbox{ and } \ y =0 . \end{cases} \]
Note the argument is a multivalued function and above formula is used to define its principle value.

Here are some examples of polar plot.

PolarPlot[3*Cos[x]+2, {x,0,2*Pi}, PlotStyle -> {Thick, Green}, PlotLabel -> Style["r = 3 cos(\[Theta]) + 2", Red,Large]]
PolarPlot[2*Cos[4*x], {x,0,2*Pi}, PlotStyle -> {Thick, Purple}, PlotLabel -> Style["r = 2 cos(4 \[Theta]) + 2", Purple,Large]]
PolarPlot[3*(1-Cos[x]), {x,0,2*Pi}, PlotStyle -> {Thick, Orange}, PlotLabel -> Style["r = 3 (1- cos(\[Theta]))", Purple,Large]]
PolarPlot[ Abs[1/2 (E^(I t) + 1)]^2, {t, 0, 2 π} , PlotStyle -> {Darker[Blue], Thick} , PlotRange -> 1.2 , PolarAxesOrigin -> {0, 1} , PolarAxes -> True , BaseStyle -> {FontFamily -> "Arial", FontSize -> 12} , PolarTicks -> {{0, Pi/4, Pi/2, (3 Pi)/4, Pi, (5 Pi)/4, (3 Pi)/2, (7 Pi)/4}, {0, .2, .4, .6, .8, 1}} , PolarGridLines -> {{0, Pi/2, Pi, 3 Pi/2}, {0.25, 0.5, 0.75, 1}} ]
or
PolarPlot[Abs[1/2 (E^(I t) + 1)]^2, {t, 0, 2 \[Pi]}, PlotStyle -> {Darker[Blue], Thick}, PolarAxes -> True, BaseStyle -> {FontFamily -> "Arial", FontSize -> 12}, PolarTicks -> {{0, Pi/4, Pi/2, (3 Pi)/4, Pi, (5 Pi)/4, (3 Pi)/2, (7 Pi)/4}, {0, .2, .4, .6, .8, 1}}, PolarGridLines -> {{0, Pi/2, Pi, 3 Pi/2}, {0.25, 0.5, 0.75, 1}}]
Polar plot as a function of tow variables:
h[r_, f_] := r^2 Cos[f] Quiet@Show[ ContourPlot[h[Sqrt[x^2 + y^2], ArcTan[x, y]], {x, 0, 1}, {y, 0, 1}, RegionFunction -> Function[{x, y, f}, 0 < ArcTan[x, y] < Pi/3 && x^2 + y^2 < 1], Contours -> 10, AspectRatio -> 1], Graphics@Circle[]]

Cycloid

The Parametrization

cycloid[a_, b_][t_] := {a*t - b*Sin[t], a - b*Cos[t]}
Manipulate[
ParametricPlot[
cycloid[a, b][t] // Evaluate, {t, -\[Pi]/2, 5*\[Pi]/2}], {a, 1, 5}, {b, 1, 5}]

 

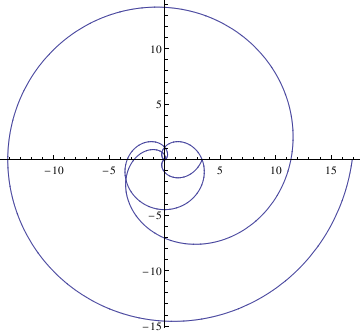
Cycloid[\[Rho]_, \[Tau]_] := {\[Rho]*\[Tau] - \[Rho]^2* Sin[\[Tau]/\[Rho]], \[Rho]^2*(1 - Cos[\[Tau]/\[Rho]])};
PolarPlot[Cycloid[1.5,theta],{theta, 0, 4*Pi}]

Here is a demonstration of ListPolarPlot:
ListPolarPlot[Table[{n, Log[n + 5]}, {n, 500}], PlotStyle -> Hue[0.11, 0.5, 1], Background -> Black]

 

Example: The butterfly curve was introduced by Temple H. Fay in 1989 and defined by the polar curve
\[ r = e^{\cos \theta} - 2\,\cos 4\theta + \sin^5 \left( \frac{\theta}{12} \right) . \]
PolarPlot[{Exp[Cos[x]] - 2*Cos[4*x]}, {x, 0, 2*Pi}, PlotStyle -> {Directive[Dashed, Thick, Purple]}]
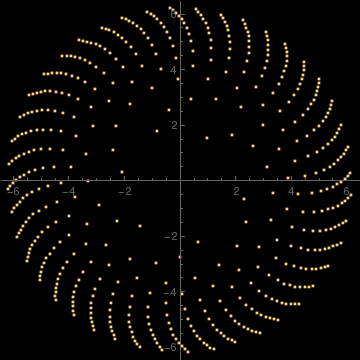
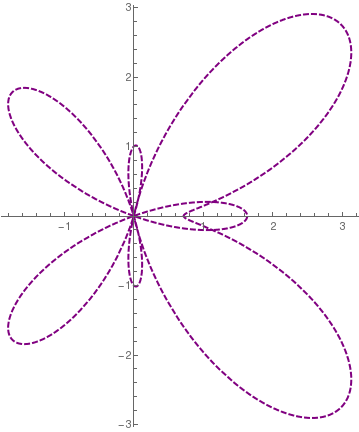
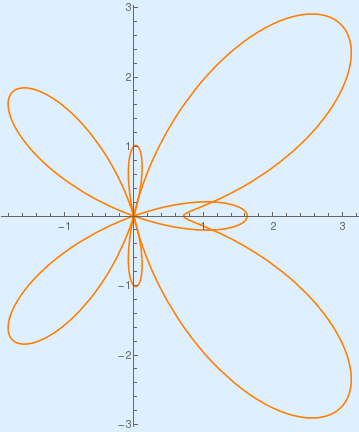
PolarPlot[{Exp[Cos[x]] - 2*Cos[4*x]}, {x, 0, 2*Pi}, PlotStyle -> {Orange}, Background -> LightBlue]
For geometrical convenience, we consider the following rotated butterfly curve instead of Fay’s butterfly curve itself: polar curve
\[ r = e^{\cos \theta} - 2\,\cos 4\theta + \sin^5 \left( \frac{\theta - \pi /2}{12} \right) . \]
r = Exp[Sin[\[Theta]]] - 2 Cos[4*\[Theta]] + Sin[(\[Theta] - Pi/2)/12]^5;
x = r*Cos[\[Theta]]; y = r*Sin[\[Theta]];
PolarPlot[r, {\[Theta], 0, 24 Pi}, Axes -> True, PlotRange -> {{-4, 4}, {-4, 4}}, Frame -> True, PlotPoints -> 1500, AspectRatio -> Automatic]

   Butterfly curve. 		         
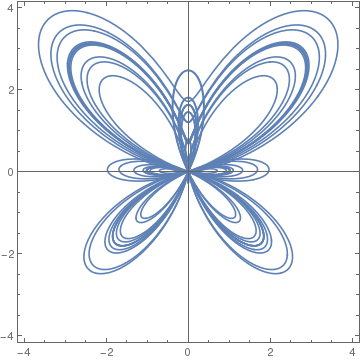
   Butterfly curve with background. 		         
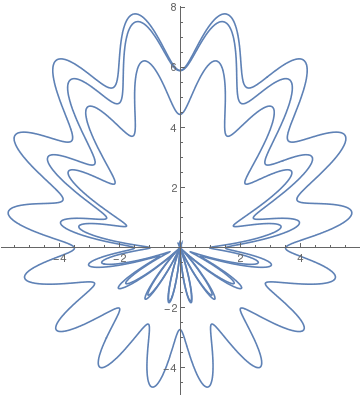
   Rotated butterfly curve.
It would be interesting to observe the unusual shapes found by considering variants of the butterfly curve:
\[ r = 2\,e^{\cos \theta} - \cos 16\theta + 3\,\sin^5 \left( \frac{2\,\theta - \pi /2}{12} \right) . \]
PolarPlot[ 2*Exp[Sin[t]] - Cos[16*t] + 3*Sin[(2*t - Pi)/12]^5, {t, 0, 6*Pi}]
The following code demonstrates how different step sizes affect a plotted image. A modified butterfly equation is used as an example. The first input [λ] of the butterfly function creates "texture" to the curve due to a rapidly changing sinusoidal factor. Any large number for λ will produce the same effect. The second input [h] is the step size. Vary the step size to see its affect! Also, by rotating the image by 90 degrees, the butterfly can be clearly seen.
butterfly[\[Lambda]_][h_, o___] := ListPolarPlot[ Table[{\[Theta], (Exp[Cos[\[Theta]]] - 2 Cos[4 \[Theta]])*(Sin[\[Lambda] \[Theta]]^4)}, {\[Theta], 0, 2 Pi, h}], o, PlotRange -> All, PlotStyle -> PointSize[Tiny]];
butterfly[99999998][0.0006]
butterfly[\[Lambda]_][h_, o___] := ListPolarPlot[ Table[{\[Theta], (Exp[Cos[\[Theta]]] - 2 Cos[4 \[Theta]])*(Sin[\[Lambda] \[Theta]]^4)}, {\[Theta], 0, 2 Pi, h}], o, PlotRange -> All, PlotStyle -> {PointSize[Tiny], Orange}, Background -> Lighter[LightBlue, 0.25]]
Rotate[%, 90 Degree]

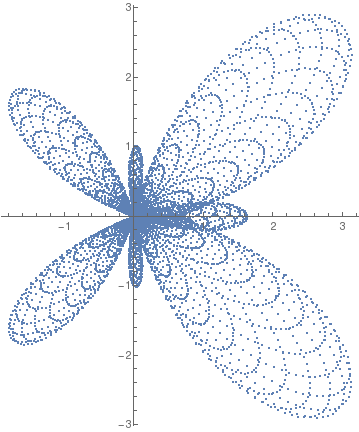
   Butterfly curve. 		         
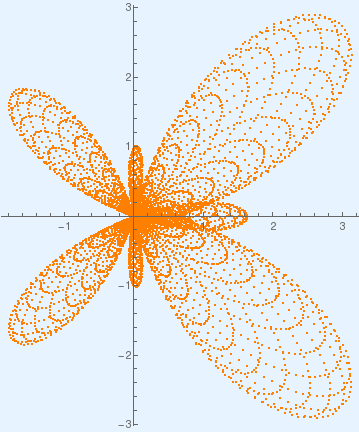
   Butterfly curve on background. 		         
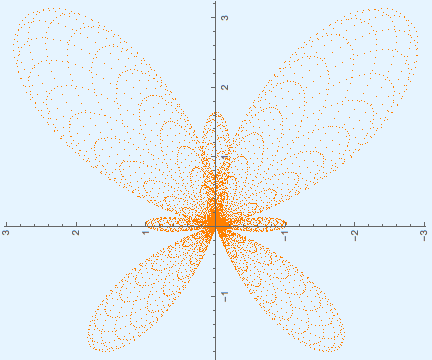
   Rotated butterfly curve.
butterfly[\[Lambda]_][h_, o___] := ListPolarPlot[ Table[{\[Theta], (Exp[Cos[\[Theta]]] - 2 Cos[4 \[Theta]])*(Sin[\[Lambda] \[Theta]]^4)}, {\[Theta], 0, 2 Pi, h}], o, PlotRange -> All, PlotStyle -> {PointSize[Tiny], Red}, Background -> Hue[0.17, 0.12, 1]]
butterfly[99999998][0.00065]
Rotate[%, 90 Degree]

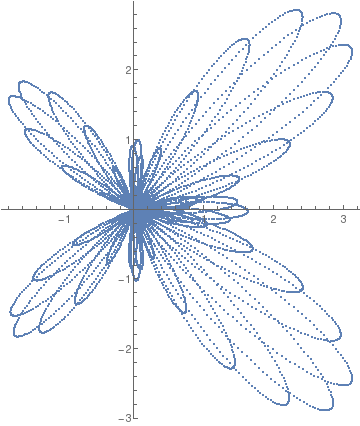
   Butterfly curve with step size 0.00065. 		         
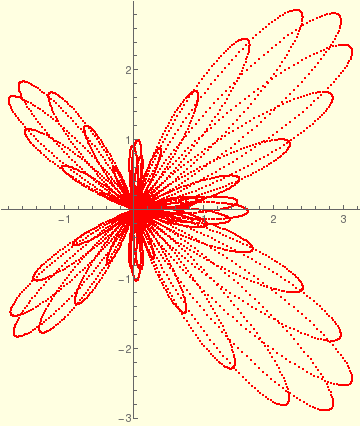
   Butterfly curve with step size 0.00065 on background. 		         
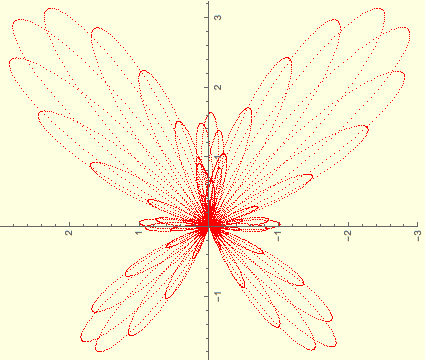
   Rotated butterfly curve curve with step size 0.00065.
butterfly[99999998][0.000169]
butterfly[\[Lambda]_][h_, o___] := ListPolarPlot[ Table[{\[Theta], (Exp[Cos[\[Theta]]] - 2 Cos[4 \[Theta]])*(Sin[\[Lambda] \[Theta]]^4)}, {\[Theta], 0, 2 Pi, h}], o, PlotRange -> All, PlotStyle -> {PointSize[Tiny], Blue}, Background -> LightPink]
butterfly[99999998][0.000169]
Rotate[%, 90 Degree]

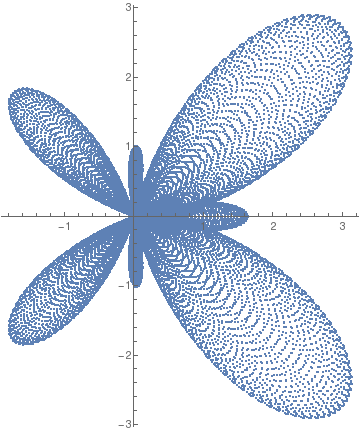
   Butterfly curve with step size 0.000169. 		         
   Butterfly curve with step size 0.000169 on background. 		         
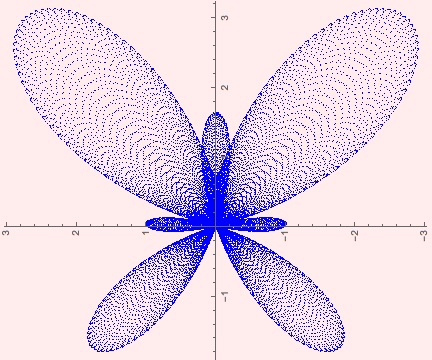
   Rotated butterfly curve curve with step size 0.000169.
■

Good examples of a polar parametrization are given by some famous spiral curves. In partocular, we mention some of them. The spiral of Archimedes is r = θ.


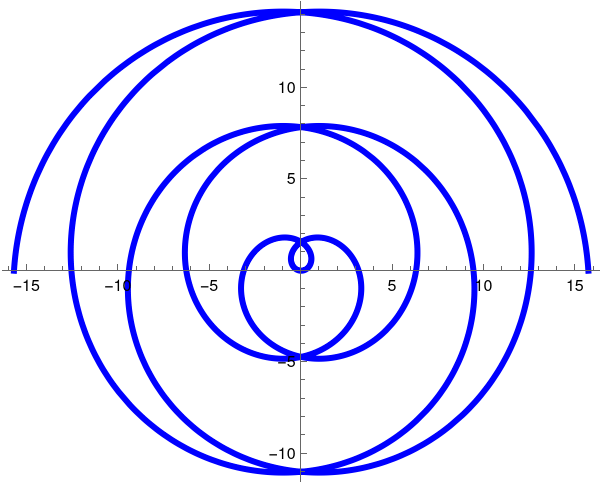
   Archimedes apiral. 		          Archimedes of Syracuse (287–212 BC) is credited with the creation of many mechanical devices such as compound pulleys, water clocks, catapults and burning mirrors. Legend has it that he was killed by a Roman soldier as he traced mathematical figures in the sand during the siege of Syracuse, at that time a Greek colony on what is now Sicily. His mathematical work included finding the area of a circle and the area under a parabola using the method of exhaustion.
PolarPlot[t, {t, -5*Pi, 5*Pi}, PlotStyle -> Thick]


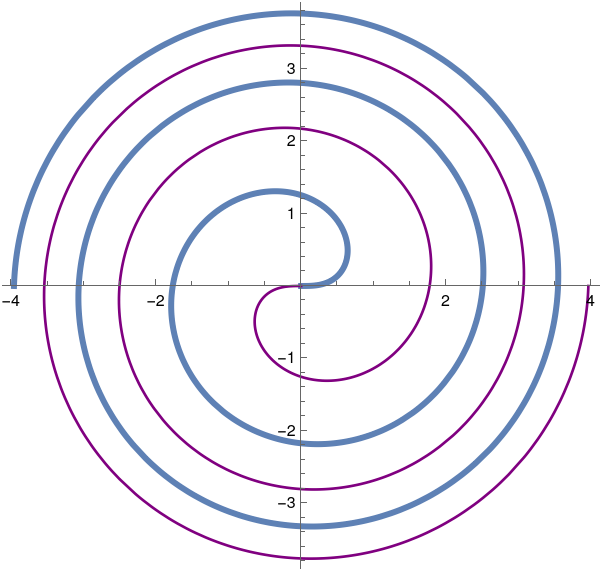
   Fermat's apiral. 		          Fermat's spiral r = ±√θ has two branches, the second obtained by allowing the radius function to be negative. The two branches join up provided the exponent is positive.
PolarPlot[{Sqrt[t], -Sqrt[t]}, {t, 0, 5*Pi}, PlotStyle -> {Thickness[0.01], Purple}]


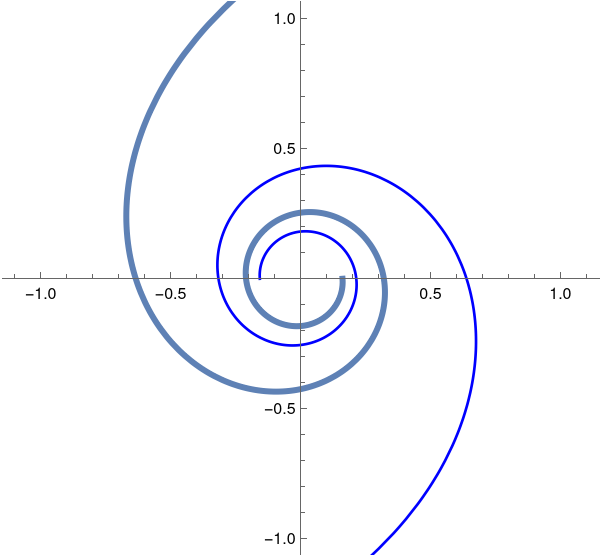
   The hyperbolic apiral. 		          The hyperbolic spiral r = ±2/θ.
PolarPlot[{2/t, -2/t}, {t, 0.3, 4*Pi}, PlotStyle -> {Thickness[0.01], Blue}]

  1. Abbena, E., Simon, S., Moder Differential Geometry of Curves and Surfaces with Mathematica,
  2. Geum, Y.H. and Kim, Y.I., On the analysis and construction of the butterfly curve using Mathematica, International Journal of Mathematical Education in Science & Technology, 2008, Vol. 39, Issue 5, pp. 670--678.
  3. Fay. T., The Butterfly curve, The American mathematical Monthly, 1989, Vol. 96, No 5, pp. 142--143.
  4. Fay. T., A study in step size, Mathematics magazine, 1997, Vol. 70, No. 2, pp. 116--117.

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)