Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Return to Part III of the course APMA0330
Glossary
Preface
This section presents three examples of a special class of iterative methods that always guarantee the convergence to the real root of the equation f(x) = 0 on some interval subject that such root exists. In particular, the bisection method is a root-finding method that repeatedly bisects an interval and then selects a subinterval in which a root must lie so that the endpoints of the subinterval become closer and closer together until we obtain an interval of arbitrarily small width that brackets the zero.
Bracketing Methods
In this section we develop in detail two bracketing methods for finding a zero/null of a real and continuous function f(x). All bracketing methods always converge, whereas open methods (discussed in the next section) may sometimes diverge. We must start with an initial interval [𝑎,b], where f(𝑎) and f(b) have opposite signs. Since the graph y = f(x) of a continuous function is unbroken, it will cross the abscissa at a zero x = α that lies somewhere within the interval [𝑎,b]. One of the ways to test a numerical method for solving the equation \( f(x) =0 \) is to check its performance on a polynomial whose roots are known. It is a custom to use some famous polynomials such as Chebyshev, Legendre or the Wilkinson polynomials:
The Bisection Method of Bolzano

Let f be a real single-valued function of a real variable. If f(α) = 0, then α is said to be a zero of f or null or, equivalently, a root of the equation f(x) = 0. It is customary to say that α is a root or zero of an algebraic polynomial f, but just a zero if f is not a polynomial. In this subsection, we discuss an algorithm for finding a root of a function, called the bisection method.
The bisection method is a very simple and robust algorithm, but it is also relatively slow. The method was invented by the Bohemian mathematician, logician, philosopher, theologian and Catholic priest of Italian extraction Bernard Bolzano (1781--1848), who spent all his life in Prague (Kingdom of Bohemia, now Czech republic). Most of Bolzano's works remained in manuscript and did not become noticed and therefore did not influence the development of the subject. Many of his works were not published until 1862 or later.
Assume that a continuous function f(x) on a given interval [𝑎, b] satisfies
The bisection method requires two initial guesses 𝑎 = x0 and b = x1 satisfying the bracket condition
f(x0)·f(x1) < 0. As the values of f(x0) and
f(x1) are on opposite sides of the x-axis y = 0, the solution α at which f(α) = 0 must reside somewhere in between of these two guesses, i.e., x0 < α < x1. While any point between the two endpoints can be chosen for the next iteration, we want to avoid the worst possible case in which the solution always happens to be in the larger of the two sections.
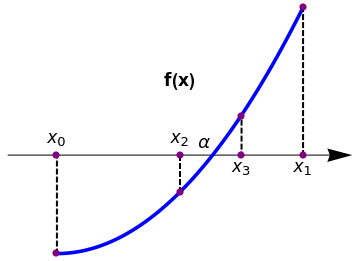
The bisection method suggests choosing the middle point in the interval [𝑎, b] as the next approximation to the root α.
The decision step for this process of interval halving is first to choose the midpoint \( c= (a+b)/2 = \left( x_0 + x_1 \right) /2 \) and then to analyze the three possibilities that might arise:
| Algorithm | Bisection (f, 𝑎, b, root, ϵ) |
|
|
plot = Plot[1*x^2, {x, 0, 1}, AspectRatio -> 1,
PlotStyle -> {Thickness[0.01], Blue}, Axes -> False,
Epilog -> {PointSize[0.03], Pink, Point[{{0, 0}, {2, 2.8}}]},
PlotRange -> {{-0.5, 1.2}, {-0.2, 1.4}}];
arrow = Graphics[{Arrowheads[0.07], Arrow[{{-0.2, 0.4}, {1.2, 0.4}}]}];
l1 = Graphics[{Thick, Dashed, Line[{{0, 0}, {0, 0.4}}]}];
l2 = Graphics[{Thick, Dashed, Line[{{0.5, 0.25}, {0.5, 0.4}}]}];
l3 = Graphics[{Thick, Dashed, Line[{{0.75, 0.54}, {0.75, 0.4}}]}];
l4 = Graphics[{Thick, Dashed, Line[{{1, 0.4}, {1, 1}}]}];
t1 = Graphics[{Black, Text[Style[Subscript[x, 0], 16], {0, 0.47}]}];
t2 = Graphics[{Black, Text[Style[Subscript[x, 1], 16], {1, 0.35}]}];
t3 = Graphics[{Black, Text[Style[Subscript[x, 2], 16], {0.5, 0.47}]}];
t4 = Graphics[{Black,
Text[Style[Subscript[x, 3], 16], {0.75, 0.35}]}];
t5 = Graphics[{Black, Text[Style[\[Alpha], 16], {0.6, 0.45}]}];
t8 = Graphics[{Black, Text[Style["f(b)", {1.08, 1}]]}];
t9 = Graphics[{Black, Text[Style["f(x)", Bold, 16], {0.5, 0.7}]}];
Show[arrow, plot, l1, l2, l3, l4, t1, t2, t3, t4, t5, t8, t9,
Epilog -> {PointSize[0.02], Purple,
Point[{{0, 0}, {0, 0.4}, {0.5, 0.4}, {0.5, 0.25}, {0.75,
0.555}, {0.75, 0.4}, {1, 0.4}, {1, 1}}]}]
|
|
| Bisection iteration. | Mathematica code |
If either of the products \( f(a)\,f(c) \quad\mbox{or} \quad f(c)\,f(b) \) is negative, we have found an interval half as wide as the original interval that contains the root, and we are “squeezing down on it.” To continue the process, relabel the new smaller interval [𝑎, b] and repeat the process until the interval is as small as desired. Since the bisection process involves sequences of nested intervals and their midpoints, we will denote by \( [a_n , b_n ] \) the subinterval obtained on the n-th stage of the bisection algorithm. Therefore, \( [a_0 , b_0 ] \) is just the starting original interval [𝑎, b]. Its midpoint we denote by \( c_0 = (a+b)/2 . \) The next interval \( [a_1 , b_1 ] \) has one of the ends c0 and the interval is half as wide as the starting one, [𝑎, b].
After arriving at the n-th interval \( [a_n , b_n ] , \) which brackets r and has midpoint cn, the new interval \( [a_{n+1} , b_{n+1} ] \) is constructed, which also brackets r and is half as wide as \( [a_n , b_n ] . \) So
Although bisection is generally slower than other methods, the neatness of the procedure (its error analysis, in particular) is a positive feature that makes bisection attractive. This method is often used in the built-in root-finding routine of programmable calculators. One disadvantage of bisection is that it cannot be used to find roots when the function is tangent to the abscissa and does not pass through it.
Module[{},
a = N[a0]; b = N[b0];
c = (a + b)/2;
k = 0;
output = {{k, a, c, b, f[c]}};
While[k < m,
If[ Sign[f[b]] == Sign[f[c]],
b = c, a = c; ];
c = (a + b)/2;
k = k + 1;
output = Append[output, {k, a, c, b, f[c]}]; ];
Print[NumberForm[
TableForm[output,
TableHeadings -> {None, {"k", "\!\(\*SubscriptBox[\(a\), \(k\)]\)", "\!\(\*SubscriptBox[\(c\), \(k\)]\)", "\!\(\*SubscriptBox[\(b\), \(k\)]\)", "f[\!\(\*SubscriptBox[\(c\), \(k\)]\)]"}}], 16]];
Print[" c = ", NumberForm[c, 16] ];
Print[" \[CapitalDelta]c = \[PlusMinus]", (b - a)/2];
Print["f[c] = ", NumberForm[f[c], 16] ]; ]
Pseudocode for Bisection Method:
input a,v,eps
external f
fa = f(a)
fb = f(b)
if f(a)*f(b) > 0 then stop
n = fix((log(b-a) - log(eps))/log(2)) + 1
for i=1 to n do
c = a+0.5*(b-a)
fc = f(c)
if fa*fc < 0 then
b = c
fb = fc
else
if fa*fc > 0 then
a = c
fa = fc
else
alpha = c
return
endif
endif
endfor
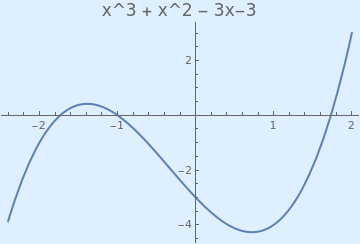
Example 1: Consider qubic equation
|
Plot[x^3 + x^2 - 3*x - 3, {x, -2.4, 2}, PlotStyle -> Thick,
PlotLabel -> Style["x^3 + x^2 - 3x-3", FontSize -> 16],
Background -> LightBlue]
|
|
| Graph of the cubic function. | Mathematica code |
The bisection method is a bracketing type root finding method in which the interval is always divided in half. If a function changes sign over an interval, the function value at the midpoint is evaluated. The location of the root is then determined as lying within the subinterval where the sign change occurs. The subinterval then becomes the interval for the next iteration. The process is repeated until the root is known to the required precision.
Now we ask Mathematica do 20 iterations and present the output in table format:
a[1] = 0; b[1] = 2;
Do[p[n] = N[1/2 (a[n] + b[n])];
If[N[f[b[n]] f[p[n]]] < 0, a[n + 1] = p[n]; b[n + 1] = b[n],
a[n + 1] = a[n]; b[n + 1] = p[n]], {n, 1, 20}]
TableForm[
Table[{a[n], b[n], p[n], N[f[a[n]]], N[f[b[n]]], N[f[p[n]]]}, {n, 1, 20}]]
0, 2, 1., -3., 3., -4.
1., 2, 1.5, -4., 3., -1.875
1.5, 2, 1.75, -1.875, 3., 0.171875
1.625, 1.75, 1.6875, -0.943359, 0.171875} -0.943359
1.625, 1.75, 1.6875, -0.943359, 0.171875, -0.409424
1.6875, 1.75, 1.71875, -0.409424, 0.171875, -0.124786
1.71875, 1.75, 1.73438, -0.124786, 0.171875, 0.0220299
1.71875, 1.73438, 1.72656, -0.124786, 0.0220299, -0.0517554
1.72656, 1.73438, 1.73047, -0.0517554, 0.0220299, -0.0149572
1.73047, 1.73438, 1.73242, -0.0149572, 0.0220299, 0.00351267
1.73047, 1.73242, 1.73145, -0.0149572, 0.00351267, -0.0057282
Example 2: Consider the function \( f(x) = e^x\, \cos x - x\, \sin x \) that has three nulls on the interval [0,10], and Mathematica confirms
FindRoot[f[x] == 0, {x, 1.5}]
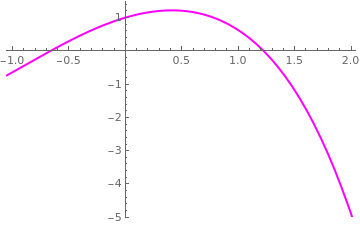 |
First, we plot the given function in a neighborhood of the origin.
f[x_] = Exp[x]*Cos[x] - x*Sin[x]
a = -1.0; b = 2.0; Bisection[a, b, 30]; Plot[f[x], {x, -1.05, 2.05}, PlotRange -> {{-1.05, 2.05}, {-5, 1.5}}, PlotStyle -> {Magenta,Thick}] |
We bracket the first root by the interval [0,3] because \( f(0)\, f(3) \approx -20.3079 . \) Dividing it in half, we choose the middle point \( c_0 =1.5, \) with \( f(0)\, f(1.5) \approx -1.17922 . \) Since the latter product is negative, our next interval will be \( [a_1 , b_1 ] = [0 , 1.5] . \) Its middle point is \( c_1 = 0.75 . \) Since \( f(0.75)\, f(1.5) \approx -1.22374 , \) we choose \( [a_2 , b_2 ] = [0.75 , 1.5] . \) Its middle point is \( c_2 = 1.125 . \) Since \( f(1.125)\, f(1.5) \approx -0.369174 , \) we choose \( [a_3 , b_3 ] = [1.125 , 1.5] . \) Again, we halve it to obtain the midpoint \( c_3 = 1.3125 . \) Since \( f(1.125)\, f(1.3125) \approx -0.100152 , \) we choose \( [a_4 , b_4 ] = [1.125 , 1.3125] . \) We can continue this process, but we see that convergence to the zero r = 1.22539 of the function f is slow: only fifth iteration gave us the first correct decimal place after the period.
Now we show step by step how it works using Mathematica. First we plot the function to roughly identify the roots.
Plot[f[x], {x, 0, 8}, PlotStyle -> {Thick, Blue}]
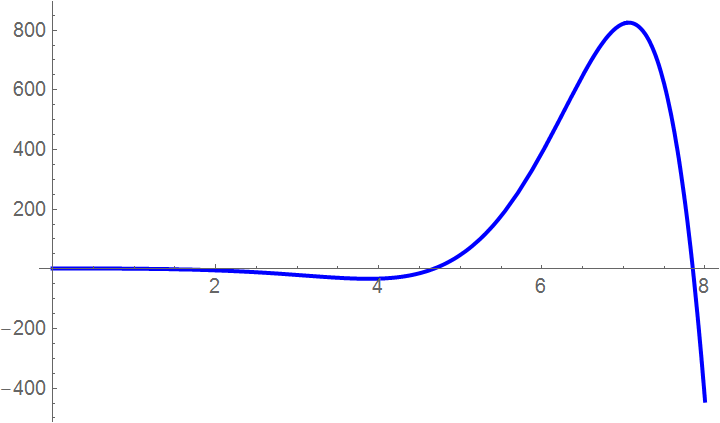
Then we define the range of x you want to see the function
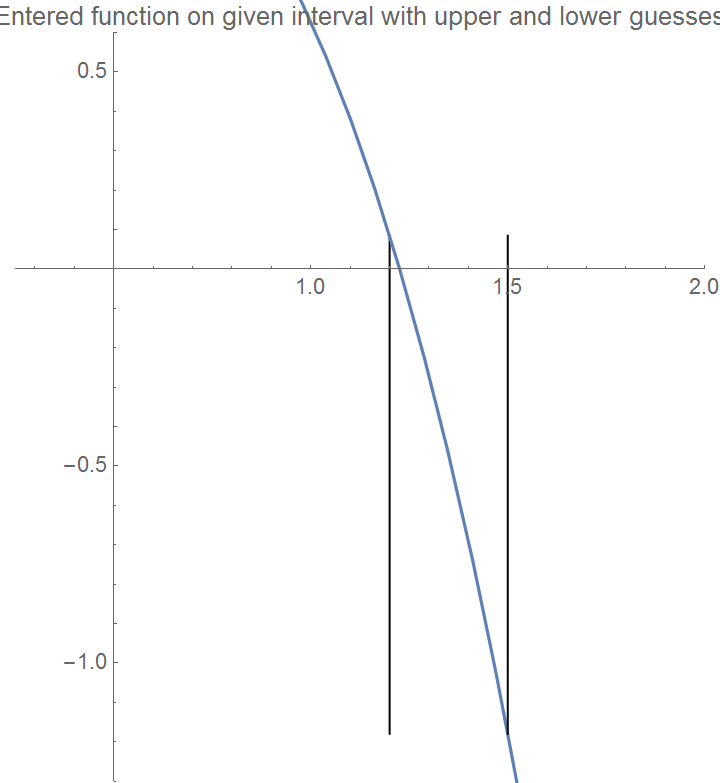
curve = Plot[f[x], {x, xa, xb}, PlotLabel -> "Entered function on given interval", LabelStyle -> {FontSize -> 11}];
step = (xb - xa)/10;
x[0] = xa;
Do[ x[i] = x[i - 1] + step; If[f[x[i]] > maxi, maxi = f[x[i]]; If[f[x[i]] < mini, mini = f[x[i]]]];
Print["i= ", i, ", x[i]= ", x[i], ", f[x[i]]= ", N[f[x[i]]]]; , {i, 1, 10}]
Show[Graphics[Line[{{xa, maxi}, {xa, mini}}]], curve, Graphics[Line[{{xb, maxi}, {xb, mini}}]], Axes -> True,
PlotLabel -> "Entered function on given interval with upper and lower guesses",
LabelStyle -> {FontSize -> 11}, PlotRange -> {{0.25, 2}, {-1.3, 0.6}}]
If[f[xa]*f[xc] <= 0, xb = xc]
N[f[xb]]
-0.472425
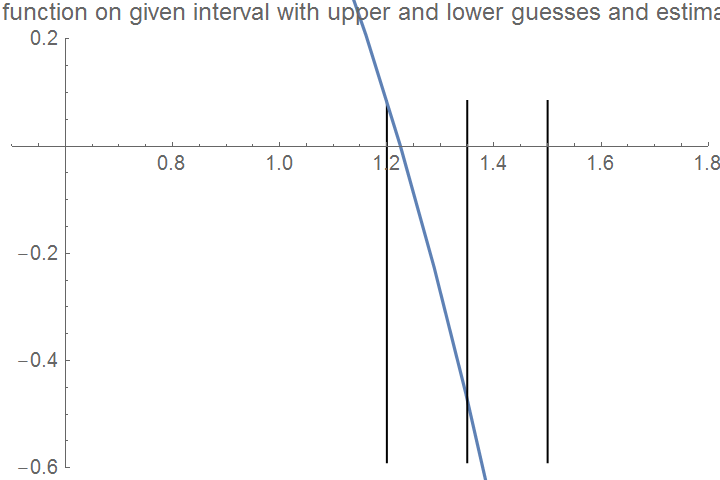
Graphics[Line[{{3/2, maxi}, {3/2, mini/2}}]],
Graphics[Line[{{27/20, maxi}, {27/20, mini/2}}]], Axes -> True,
PlotLabel -> "Entered function on given interval with upper and lower guesses
and estimated root", LabelStyle -> {FontSize -> 10}, PlotRange -> {{0.5, 1.8}, {-0.6, 0.2}}]
N[xc]
1.275
If[f[xa]*f[xc] <= 0, xb = xc]
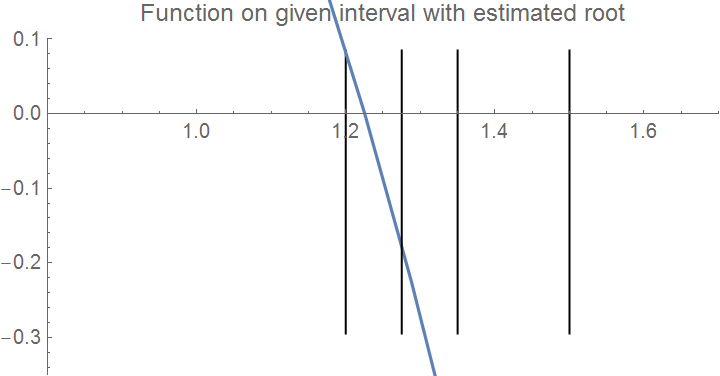
Graphics[Line[{{3/2, maxi}, {3/2, mini/4}}]],
Graphics[Line[{{51/40, maxi}, {51/40, mini/4}}]],
Graphics[Line[{{27/20, maxi}, {27/20, mini/4}}]], Axes -> True,
PlotLabel -> "Function on given interval with estimated root",
LabelStyle -> {FontSize -> 10}, PlotRange -> {{0.8, 1.7}, {-0.35, 0.1}}]
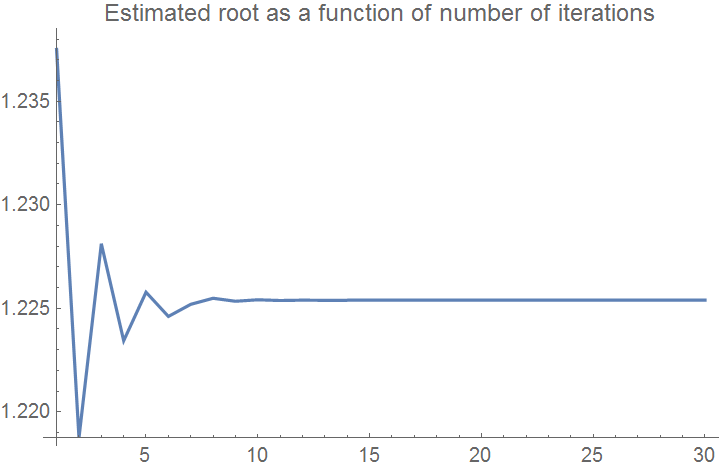
Here the bisection method algorithm is applied to generate the values of the roots, true error, absolute relative true error, approximate error, absolute relative approximate error, and the number of significant digits at least correct in the estimated root as a function of number of iterations.
For[i = 1; xu = xb; xl = xa, i <= nmaximum, i++, xr[i] = (xu + xl)/2;
If[f[xr[i]]*f[xu] <= 0, xl = xr[i], xu = xr[i]]]
s = FindRoot[Exp[x]*Cos[x] - x*Sin[x] == 0, {x, 1.2}]
xactual = Evaluate[x /. s]
For[i = 1, i <= nmaximum, i++, Et[i] = Abs[xactual - xr[i]]]
For[i = 1, i <= nmaximum, i++, et[i] = Abs[Et[i]/xactual*100]]
For[i = 1, i <= nmaximum, i++, If[i <= 1, Ea[i] = 0, Ea[i] = Abs[xr[i] - xr[i - 1]]]]
For[i = 1, i <= nmaximum, i++, If[i <= 1, ea[i] = 0, ea[i] = Abs[Ea[i]/xr[i]*100]]]
For[i = 1, i <= nmaximum, i++,
If[(ea[i] >= 5) || (i <= 1), sigdig[i] = 0,
sigdig[i] = Floor[(2 - Log[10, Abs[ea[i]/0.5]])]]]
ListPlot[xrplot, Joined -> True, PlotRange -> All,
AxesOrigin -> {1, Min[xrplot]},
PlotLabel -> "Estimated root as a function of number of iterations"]
ListPlot[Etplot, Joined -> True, PlotRange -> All,
AxesOrigin -> {1, Min[Etplot]},
PlotLabel -> "Absolute true error as a function of number of iterations"]
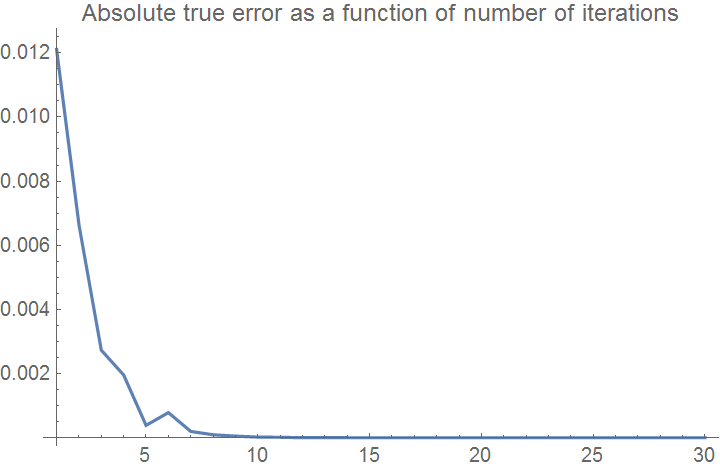
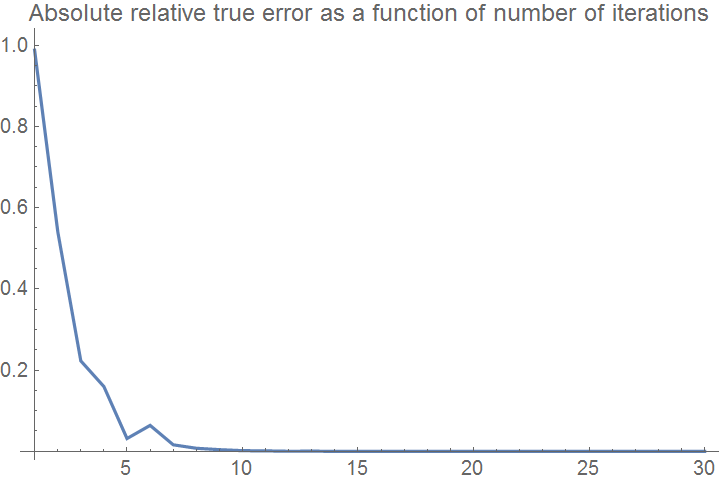
ListPlot[etplot, Joined -> True, PlotRange -> All,
AxesOrigin -> {1, Min[etplot]},
PlotLabel -> "Absolute relative true error as a function of number of iterations"]
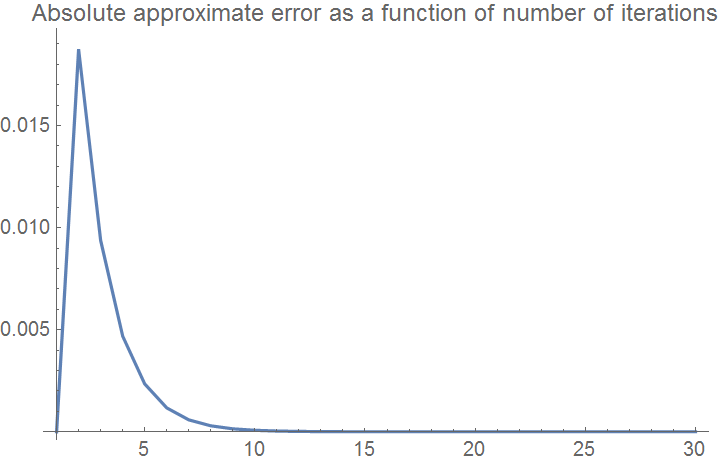
ListPlot[Eaplot, Joined -> True, PlotRange -> All,
AxesOrigin -> {1, Min[Eaplot]}, PlotLabel ->
"Absolute approximate error as a function of number of iterations"]
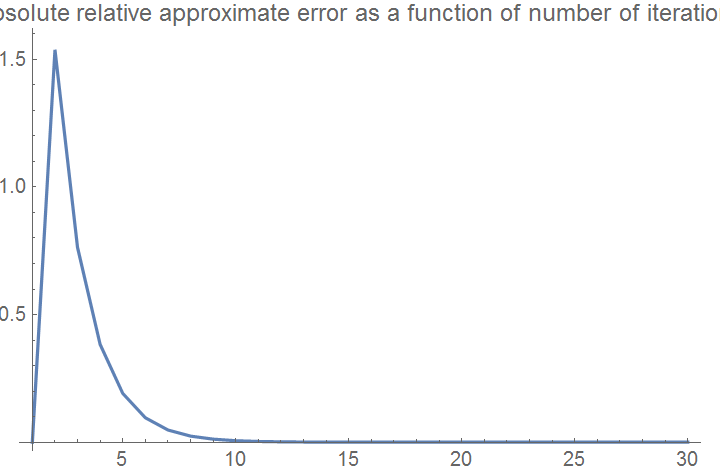
ListPlot[eaplot, Joined -> True, PlotRange -> All,
AxesOrigin -> {1, Min[eaplot]}, PlotLabel ->
"Absolute relative approximate error as a function of number of iterations"]
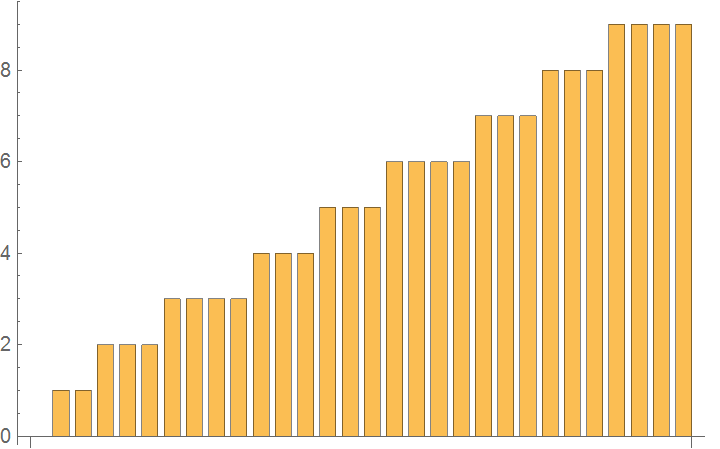
BarChart[sigdigplot]
We present some scripts for the application of the bisection method. First, we type in a subroutine for halving the interval.
Module[{interval}, interval = {a, (a + b)/2, b};
Last@Flatten[ Select[Thread@(Partition[#, 2, 1] & /@ {Sign /@ (func /@ interval), interval}),
Times @@ (First@#) < 0 &], 1]]
NestWhile[shrinkInterval[func, #] &, {a0, b0}, Abs@(Subtract @@ #) > \[Xi] &]
a[1] = 0;
b[1] = 3;
Do[p[n] = N[1/2 (a[n] + b[n])];
If[N[f[b[n]] f[p[n]]] < 0, a[n + 1] = p[n]; b[n + 1] = b[n],
a[n + 1] = a[n]; b[n + 1] = p[n]], {n, 1, 20}]
TableForm[ Table[{a[n], b[n], p[n], N[f[a[n]]], N[f[b[n]]], N[f[p[n]]]}, {n, 1, 20}]]
f[x_] = Exp[x]*Cos[x] - x*Sin[x]
Plot[f[x], {x, 0, 9}];
a = Input["Enter a"];
b = Input["Enter b"];
tol = Input["Enter tolerance"];
n = Input["Enter total iteration"]; If[f[a]*f[b] > 0, {Print["No solution exists"] Exit[]}];
Print[" n a b c f(c)"];
Do[{c = (a + b)/2; If[f[a]*f[c] > 0, a = c, b = c],
Print[PaddedForm[i, 5], PaddedForm[N[a], {10, 6}], PaddedForm[N[b], {10, 6}], PaddedForm[N[c], {10, 6}], PaddedForm[N[f[c]], {10, 6}]]
If[ Abs[a - b] < tol, {Print["The solution is: ", c] Exit[]}]}, {i, 1, n}]; Print["The maximum iteration failed"];
False Position Method
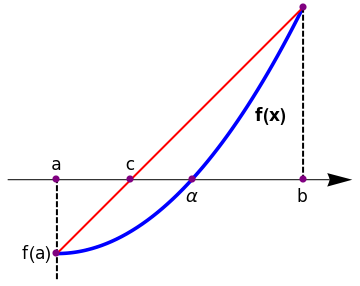
The poor convergence of the bisection method as well as its poor adaptability to higher dimensions (i.e., systems of two or more non-linear equations) motivate the use of better techniques. Another popular algorithm is the method of false position or the regula falsi method. A better approach is obtained if we find the point c on the abscissa where the secant line crosses it. To determine the value of c, we write down two versions of the slope m f the line that connects the points \( (a, f(a)) \quad\mbox{and} \quad (b, f(b)) : \)
- If f(a) and f(c) have opposite signs, a zero lies in [a,c] .
- If f(b) and f(c) have opposite signs, a zero lies in [c,b] .
- If \( f(c) =0 , \) then the zero is c.
|
plot = Plot[1*x^2, {x, 0, 1}, AspectRatio -> 1,
PlotStyle -> {Thickness[0.01], Blue}, Axes -> False,
Epilog -> {PointSize[0.03], Pink, Point[{{0, 0}, {1, 1}}]},
PlotRange -> {{-0.2, 1.2}, {-0.2, 1.4}}];
line = Graphics[{Thick, Red, Line[{{0, 0}, {1, 1}}]}]; arrow = Graphics[{Arrowheads[0.07], Arrow[{{-0.2, 0.3}, {1.2, 0.3}}]}]; l1 = Graphics[{Thick, Dashed, Line[{{0, -0.1}, {0, 0.3}}]}]; l3 = Graphics[{Thick, Dashed, Line[{{1, 0.3}, {1, 1}}]}]; t1 = Graphics[{Black, Text[Style["a", 16], {0, 0.36}]}]; t3 = Graphics[{Black, Text[Style["f(a)", 16], {-0.08, 0.0}]}]; t4 = Graphics[{Black, Text[Style[\[Alpha], 16], {0.55, 0.23}]}]; t5 = Graphics[{Black, Text[Style["c", 16], {0.3, 0.36}]}]; t6 = Graphics[{Black, Text[Style["b", 16], {1, 0.23}]}]; t8 = Graphics[{Black, Text[Style["f(b)", {1.08, 1}]]}]; t9 = Graphics[{Black, Text[Style["f(x)", Bold, 16], {0.87, 0.56}]}]; Show[arrow, plot, line, l1, l3, t1, t3, t4, t5, t6, t8, t9, Epilog -> {PointSize[0.02], Purple, Point[{{0, 0}, {0, 0.3}, {0.3, 0.3}, {0.55, 0.3}, {1, 1}, {1, 0.3}}]}] |
|
| Regula Falsi. | Mathematica code |
The decision process is the same as in bisection method and we generate a sequence of intervals \( \left\{ [a_n , b_n ]\right\} \) each of which brackets the null. At each step the approximation of the zero r is
Example 3: We reconsider the function \( f(x) = e^x\, \cos x - x\, \sin x \) on interval [0,3]. From the previous example, we know that f has the null r = 1.22539. We ask Mathematica for help:
a = Input["Enter a"];
b = Input["Enter b"];
tol = Input["Enter tolerance"];
n = Input["Enter total iteration"];
x0 = a;
x1 = b;
If[f[x0]*f[x1] > 0, {Print["There is no root in this interval"], Exit[]}];
Print[" n x0 x1 x2 f(x2)"];
Do[x2 = x0 - (f[x0]/(f[x1] - f[x0]))*(x1 - x0) // N;
Print[PaddedForm[i, 5], PaddedForm[x0, {12, 6}],
PaddedForm[x1, {12, 6}],
PaddedForm[x2, {12, 6}], PaddedForm[f[x2], {12, 6}]];
If[Abs[x2 - x1] < tol || Abs[x2 - x0] < tol, {Print["The root is: ", x2], Exit[]}];
If[f[x0]*f[x2] > 0, x0 = x2, x1 = x2], {i, 1, n}];
Print["Maximum iteration failed"];
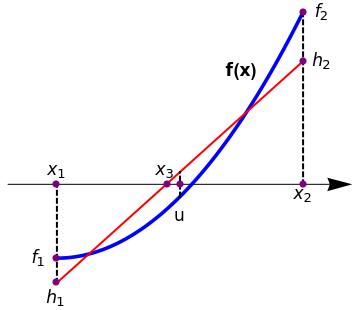
Ridders’ Method
|
plot = Plot[1*x^2, {x, 0, 1}, AspectRatio -> 1,
PlotStyle -> {Thickness[0.01], Blue}, Axes -> False, PlotRange -> {{-0.2, 1.2}, {-0.2, 1.4}} ]
line = Graphics[{Thick, Red, Line[{{0, -0.1}, {1, 0.8}}]},
Epilog -> {PointSize[0.03], Pink, Point[{{0.5, 0.5}}]}];
arrow = Graphics[{Arrowheads[0.07], Arrow[{{-0.2, 0.3}, {1.2, 0.3}}]}]; l1 = Graphics[{Thick, Dashed, Line[{{0, -0.1}, {0, 0.3}}]}]; l2 = Graphics[{Thick, Dashed, Line[{{0.5, 0.25}, {0.5, 0.35}}]}]; l3 = Graphics[{Thick, Dashed, Line[{{1, 0.3}, {1, 1}}]}]; t1 = Graphics[{Black, Text[Style[Subscript[x, 1], 16], {0, 0.36}]}]; t2 = Graphics[{Black, Text[Style[Subscript[h, 1], 16], {0, -0.16}]}]; t3 = Graphics[[{Black, Text[Style[Subscript[f, 1], 16], {-0.08, 0.0}]}]; t4 = Graphics[{Black, Text[Style["u", 16], {0.5, 0.17}]}]; t5 = Graphics[{Black, Text[Style[Subscript[x, 3], 16], {0.44, 0.36}]}]; t6 = Graphics[{Black, Text[Style[Subscript[x, 2], 16], {1, 0.26}]}]; t7 = Graphics[{Black, Text[Style[Subscript[h, 2], 16], {1.08, 0.8}]}]; t8 = Graphics[{Black, Text[Style[Subscript[f, 2], 16], {1.08, 1}]}]; t9 = Graphics[{Black, Text[Style["f(x)", Bold, 16], {0.75, 0.76}]}]; Show[arrow, plot, line, l1, l2, l3, t1, t2, t3, t4, t5, t6, t7, t8, t9, Epilog -> {PointSize[0.02], Purple, Point[{{0, -0.1}, {0, 0}, {0, 0.3}, {0.45, 0.3}, {0.5, 0.3}, {1, 0.8}, {1, 1}, {1, 0.3}}]}] |
|
| Ridders’ algorithm. | Mathematica code |
When a root is bracketed between x1 and x2, Ridders’ method first evaluates the function h(x) at the midpoin \( u = \left( x_1 + x_2 \right) /2 . \) Then for three equidistance x-values x1, u, and x2, the following requirement for the straight line connecting points (x1, f1) and (x2, f2) is met:
| Algorithm: | Ridders’ rule for determination of the root of the equation f(x) = 0 |
|
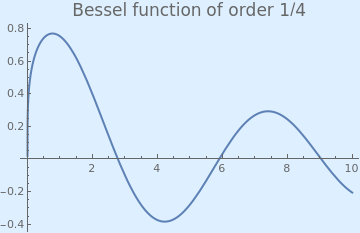
Example 4: Consider the Bessel function of the first kind of order 1/4:
|
We plot the Bessel function with the following Mathematica code:
Plot[BesselJ[1/4, x], {x, 0, 10}, PlotStyle -> Thick,
PlotLabel -> Style["Bessel function of order 1/4", FontSize -> 16],
Background -> LightBlue]
|
|
| Bessel function of order 1/4. | Mathematica code |
Since the Bessel function has a positive value at x = 2
Location of Roots
To roughly estimate the locations of the roots of the equation \( f(x) =0 \) over the interval [a,b], it make sense to make a uniform partition of the interval by sample points \( \left( x_n , y_n = f(x_n )\right) \) and use the following criteria:
- Ridders, C.J.F., A New Algorithm for Computing a Single Root of a Real Continuous Function, IEEE Transactions on Circuits and Systems, 1979, vol. CAS-26, No. 11, pp. 979–980.
Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)