Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the course APMA0330
Return to the main page for the course APMA0340
Return to the main page for the course APMA0360
Return to Part VI of the course APMA0330

Glossary

Preface

This section discusses a qualitative approach to the study of differential equations, and obtain qualitative information about the solutions directly from the differential equation, without actuallly finding a solution formula.

Direction Fields

For any differential equation in normal form

\[ y' = f(x,y) \qquad \mbox{or} \qquad \frac{{\text d}y}{{\text d}x} = f(x,y) \]
where f(x,y) is a well defined in some domain slope function. It is possible to obtain a graphical information about general behavior of the solution curves (are also called trajectories) from the differential equation itself without finding the equation that represents an actual solution.
A direction field or a slope field for a first order differential equation \( {\text d}y / {\text d}x = f(x,y) , \) is a field of short either straight line segments or arrows of slope f(x,y) drawn through each point (x,y) in some chosen grid of points in the (x,y) plane.

A striking way to visualize direction fields uses a magnet with iron filings dusted over a thin card placed horizontally and immediately above the magnet. Each iron filing becomes magnetized and tends to set itself in the direction of the resultant force at its mid-point. If the arrangement of the fillings is aided by gently tapping the card, the filings will distribute themselves approximately along the lines of force. Hence, each individual filing acts as a line-element through its mid-point. You can see many images of this at Google Images, putting "google images iron filings over a magnet" in your browser search bar, as for instance https://www.pinterest.com/ikesuorg/iron-filings/.

Direction fields could be visualized by plotting a list of vectors that are tangent to solution curves. It is as if we had a traffic policeman stationed at each point (x,y) on the plane and directed the traffic to flow along the direction specified by the slope function f(x,y). From this point of view, a solution is a curve that obeys the law at each of its points. Correspondingly, Mathematica uses a special command to plot direction fields: VectorPlot. It requires vector-valued input: one for abscissa (usually labeled by x or t) and another for ordinate. Therefore, to plot a direction field for a first order differential equation \( {\text d}y / {\text d}x = f(x,y) , \) a user needs to set 1 for the first coordinate and f(x,y) for the second one, so making the vector input \( \left( 1, f(x,y) \right) . \) Besides, Mathematica also offers their variations:
ListVectorPlot,
VectorDensityPlot, and
ListVectorDensityPlot.

Their applications will be clear from presented examples here and within first two parts.

Since by default, VectorPlot automatically enlarges/stretches the lengths of vectors, Mathematica offers an option, VectorScale to suppress changes in vector lengths. Let us look at two outputs generated without and with this option:

VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}] /. ar : Arrow[{p1_, p2_}] :> Tooltip[Arrow[{p1, p2}], p1]
and (we just changed the orientation, for fun)
VectorPlot[{-y, +x}, {x, -4, 4}, {y, -4, 4}, VectorScale -> {0.045, 0.9, None}, VectorPoints -> 16]

   
Vector plot with scaling (left) and without (right).
Notice in the upper right quadrant of the plot below, we have emphasized two of the arrows by adding a graphic point to the end (with a circle around it merely to draw your attention to it). The point represents the point of tangency the line portion of the arrow has with the (not shown) curve represented by a particular equation. The head of the arrow points in the direction of the next step on the curve. If you hover your mouse over the head of the arrow you see the coordinates of the point to which it is attached
vp1 = VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}] /. ar : Arrow[{p1_, p2_}] :> Tooltip[Arrow[{p1, p2}], p1];
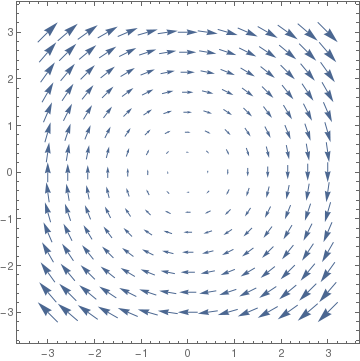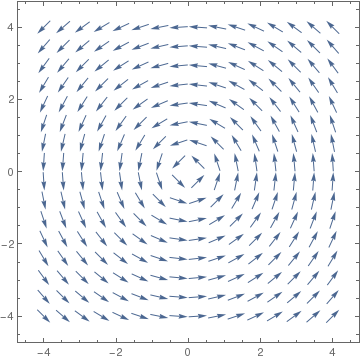pts = {{1.35386, 2.68245}, {0.416358, 1.05865}};
ptsG = Graphics[{{PointSize[Medium], Orange, Point[pts[[1]]]}, {PointSize[Medium], Blue, Point[pts[[2]]]}}];
cir = Graphics[{Circle[pts[[1]], .1], Circle[pts[[2]], .1]}];
Show[vp1, ptsG , cir]

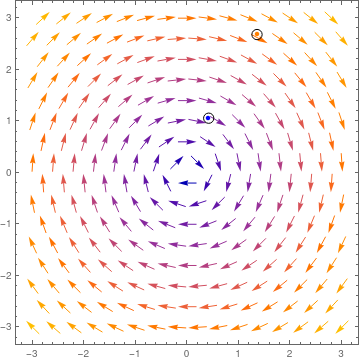
Sometimes we need to include axes into the direction field; this can be achieved, for instance, by enlarging the plotted area, as the following examples show.

sys1 = {u (1 - u + a v), r v (1 - v + b u)};
vp1 = VectorPlot[ sys1 /. {a -> 1/4, b -> 2, r -> 1}, {u, 0, 2}, {v, 0, 2}, VectorScale -> {0.045, 0.9, None}, VectorStyle -> {GrayLevel[0.2]}, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}];
sys2 = {u (1 - u + a v), r v (1 - v + b u)};
vp2 = VectorPlot[ sys2 /. {a -> 1/4, b -> 2, r -> 1}, {u, -0.2, 2}, {v, -0.2, 2}, VectorScale -> {0.045, 0.9, None}, VectorStyle -> {GrayLevel[0.2]}, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}];
GraphicsRow[{vp1, vp2}, Frame -> All]

   
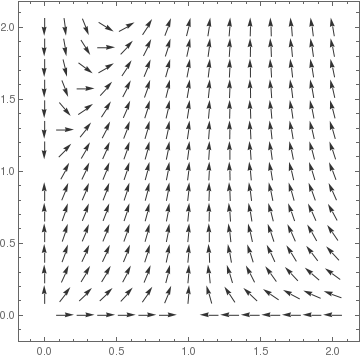Vector plot without axes (left) and with axes (right).

Ideally we'd get something like a tool-tip which shows the x,y position where I click (or where the mouse is currently hovering) and the evaluated vector (or scalar in the case of a scalar field) at that position. I think this would be a great way to "get a feel for" the values because by default the arrows are scaled automatically so they fit so I don't know anything about the relative magnitude of a particular arrow.

VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}] /. ar : Arrow[{p1_, p2_}] :> Tooltip[Arrow[{p1, p2}], p1]
There are many ways to do this. For example, using LocatorPane[{x,y}, back] that represents a pane with a locator at position {x,y} and background back Also, Mathematica offers a dynamic version of this command: LocatorPane[Dynamic[pt], back] that takes the locator position to be the dynamically updated current value of pt, with the value of pt being reset if the locator is moved. Imagine this is your vector function:
f[x_, y_] := {-1 - x^2 + y, 1 + x - y^2}

Now this will do the trick, where first line is the coordinate, and second is the function f evaluated at the coordinate. Red dot will follow the mouse. You can also bring the numbers with PlotLabel outside the graphics not to block the view. Since the plot itself is static you can also do VectorPlot[..., Epilog -> Dynamic[...]] instead of Dynamic[VectorPlot[....]]. On my system this makes the plot a lot more responsive.
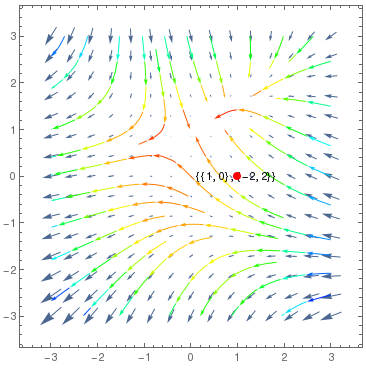
DynamicModule[{pt = {1, 0}},LocatorPane[Dynamic[pt],
VectorPlot[f[x, y], {x, -3, 3}, {y, -3, 3}, StreamPoints -> Coarse,
StreamColorFunction -> Hue, Epilog -> Dynamic@Inset[{pt, f @@ pt}, pt],
PerformanceGoal -> "Quality"], AutoAction -> True, Appearance -> Style["\[FilledCircle]", Red]]]
Direction field for the vector equation.
and then we export the figure
Export["pointdir.png", %]

We show how to use them by examples.

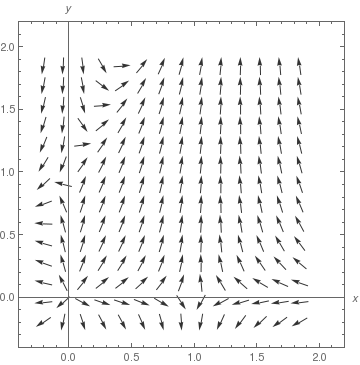
VectorPlot[{1, (y + Exp[x/2])/(x + Exp[y])}, {x, 0, 3}, {y, -1, 2}]

 One can draw the direction field either with arrows

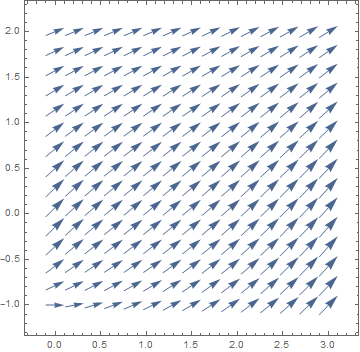
VectorPlot[{1, y^3 - 8*x}, {x, -1, 5}, {y, -5, 5}, VectorPoints -> 16, VectorStyle -> Arrowheads[0.028], Axes -> True]

or with drop feature

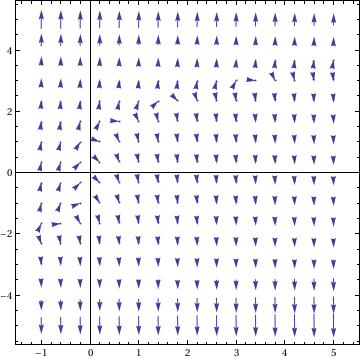
VectorPlot[{1, y^3 - 8*x}, {x, -1, 5}, {y, -5, 5}, VectorPoints -> 10, VectorStyle -> "Drop", Axes -> True]
Some other examples.
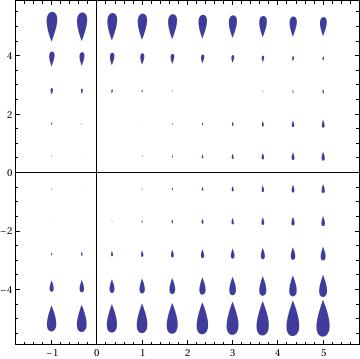VectorPlot[{-1 - y^2 + x, 1 + x - 2 y^3}, {x, -3, 3}, {y, -6, 6}, StreamPoints -> Coarse, StreamScale -> Full, StreamStyle -> Arrowheads[{{0.03, Automatic, Graphics[Circle[]]}}]]
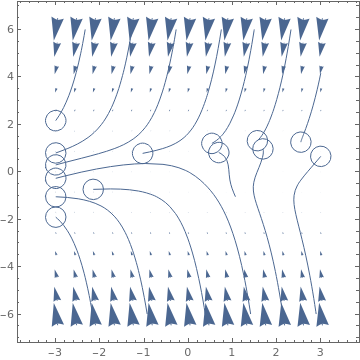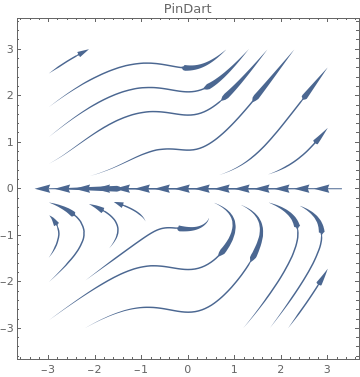
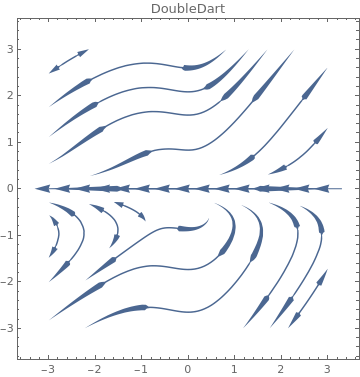
Table[VectorPlot[{-1+x^2-3y,7+2x-y},{x,-3,3},{y,-3,3},PlotLabel->s,StreamPoints->Coarse,StreamScale->{Full,All,0.05},StreamStyle->s],{s,{"Segment","Line"}}]
Table[VectorPlot[{-2 - y^2 + x, 1 + 7 x - y^3}, {x, -3, 3}, {y, -3,
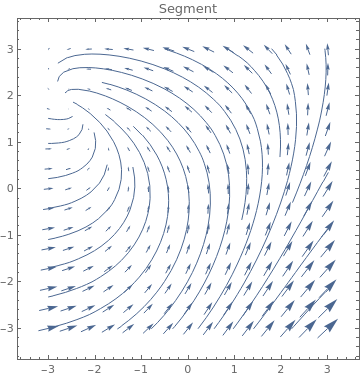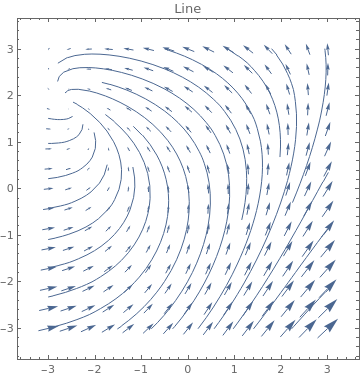3}, PlotLabel -> s, StreamPoints -> Coarse,
StreamScale -> {Full, All, 0.05},
StreamStyle -> s], {s, {"Arrow", "ArrowArrow", "CircleArrow"}}]
Table[VectorPlot[{-1 - y^2 + 3 x, -5 + 6 x - 3 y^3}, {x, -3,
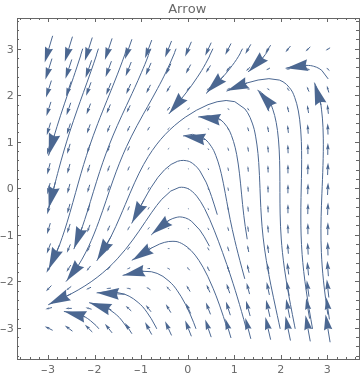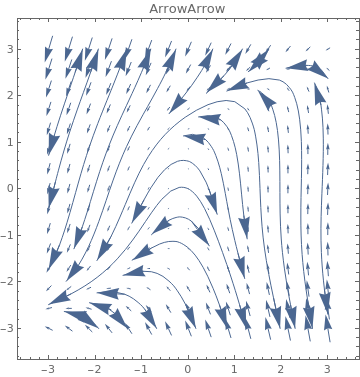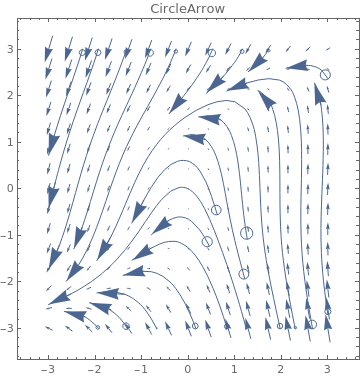3}, {y, -3, 3}, PlotLabel -> s, StreamScale -> {Full, All, 0.03}, StreamPoints -> Coarse,
StreamStyle -> s], {s, {"BarDot", "Dot", "DotArrow", "DotDot"}}
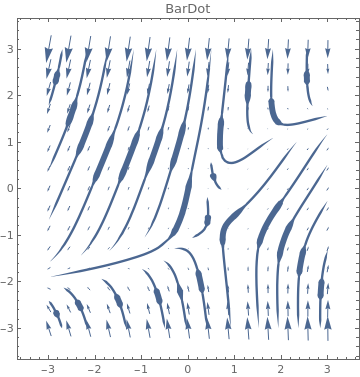Table[VectorPlot[{-1-4x^2+2y^3,-6+x-1.01y^3},{x,-3,3},{y,-3,3},PlotLabel->s,StreamScale->{Full,All,0.03},StreamPoints->Coarse,StreamStyle->s],{s,{"Drop","BackwardPointer","Pointer","Toothpick"}}]
Table[VectorPlot[{1+x^-2+y^-3,1+x^-1+y^-2},{x,-3,3},{y,-3,3},PlotLabel->s,StreamScale->{Full,All,0.03},StreamPoints->Coarse,StreamStyle->s],{s,{"Dart","PinDart","DoubleDart"}}]

 

ListVectorPlot

data = Table[{-1 + 2 x^2 + y, 1 - 3 x + y^2}, {x, -3, 3, 0.2}, {y, -3, 3, 0.2}];
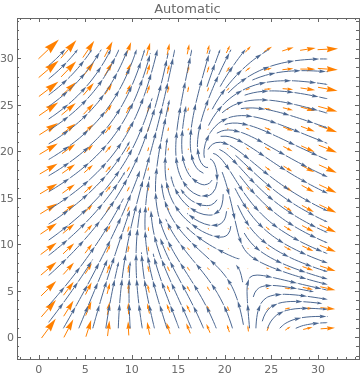
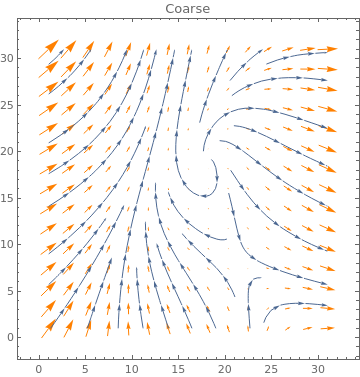
Table[ListVectorPlot[data, VectorStyle -> Orange, StreamPoints -> p,
PlotLabel -> p], {p, {Automatic, Coarse, Fine}}]
data = Table[{-1 + 2 x^2 + y, 1 - 3 x + y^2}, {x, -3, 3, 0.2}, {y, -3, 3, 0.2}];
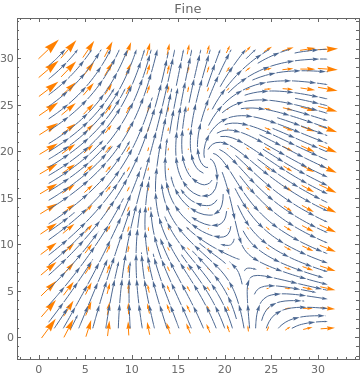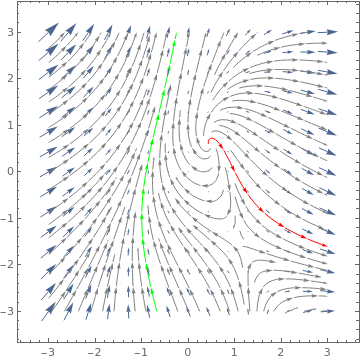
ListVectorPlot[data, DataRange -> {{-3, 3}, {-3, 3}}, StreamStyle -> Gray,
StreamPoints -> {{{{1, 0}, Red}, {{-1, -1}, Green}, Automatic}}]
data = Table[{y, -x}, {x, -2, 4, 0.7}, {y, -2, 4, 0.7}];
Table[ListVectorPlot[data, PlotLabel -> n, VectorStyle -> Orange,
StreamPoints -> Coarse, StreamScale -> {Full, n}], {n, {10, All}}]
ListVectorPlot3D[ Table[{x, y, z}, {x, -1, 2, .5}, {y, -1, 2, .5}, {z, -1, 2, .5}]]

 

VectorDensityPlot

Use VectorDensityPlot to visualize the field densities:
f[x_, y_] = (y + Exp[x/2])/(x + Exp[y])
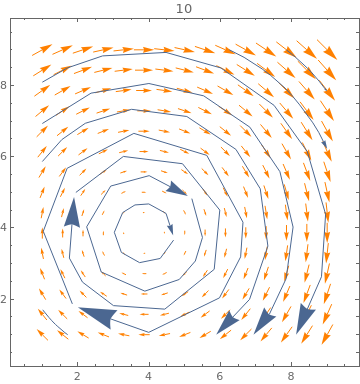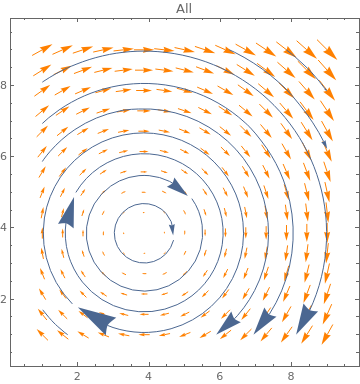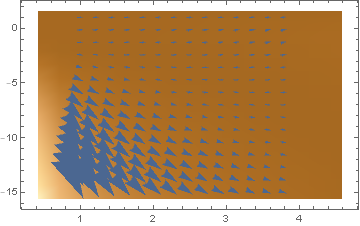
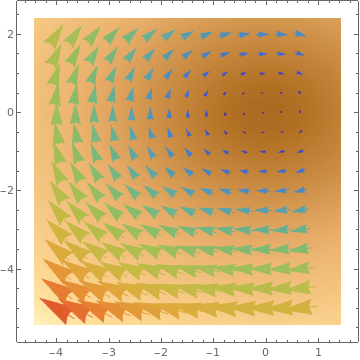
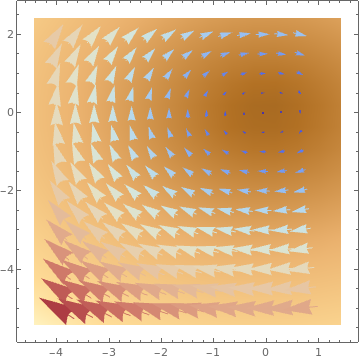
VectorDensityPlot[{1, f[x, y]}, {x, 1, 4}, {y, -15, 1}, AspectRatio -> 1/GoldenRatio]
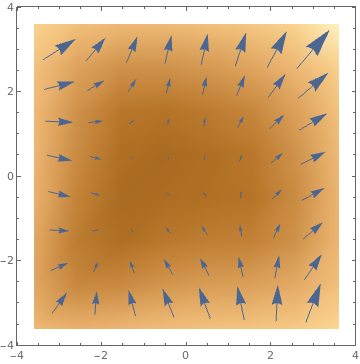
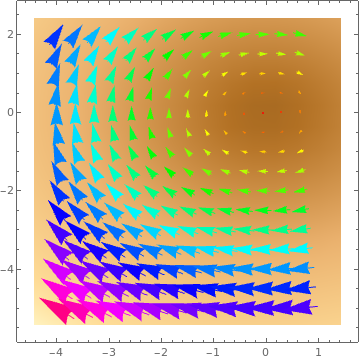
VectorDensityPlot[{-1 + x^2 + y, 1 + x + y^2}, {x, -3, 3}, {y, -3, 3}, VectorPoints -> 8]
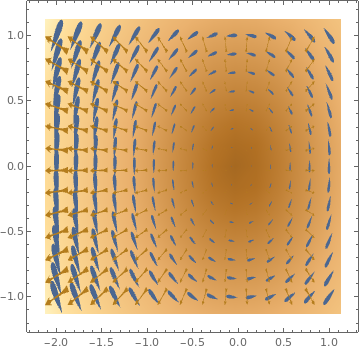
Table[VectorDensityPlot[{y, -x}, {x, -4, 1}, {y, -5, 2}, VectorScale -> Large, VectorColorFunction -> k], {k, {Hue, "Rainbow", "ThermometerColors"}}]
VectorDensityPlot[{{y, -x}, {x, y}}, {x, -2, 1}, {y, -1, 1}, VectorMarkers -> {"Drop", "Dart"}]
VectorDensityPlot[{-1 + 2 x^2 + y, 1 - 3 x + y^2}, {x, -3, 3}, {y, -3, 3}, VectorPoints -> 18, VectorStyle -> Arrowheads[0]]
VectorDensityPlot[{x, y}, {x, -.5, 4}, {y, -2, 3}, VectorPoints -> 8, PlotRange -> All,
VectorStyle -> Arrowheads[{{0.03, Automatic,
Graphics[Rectangle[{-0.5, -0.5}, {0.5, 0.5}]]}, {0.03, Automatic, Graphics[Circle[]]}}]]
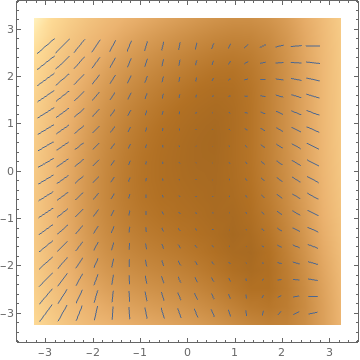
VectorDensityPlot[{{-1 + 2 x^2 + y, 1 - 3 x + y^2}, {(1 + x - y^2),
1 - .5 x^2 + y}}, {x, -3, 3}, {y, -3, 3}, VectorPoints -> 8, VectorStyle -> {Red, Blue}]

 

ListVectorDensityPlot

data = Table[{{x, -y} = RandomReal[{-1.5, 1.5}, {2}], {{y, x + x^3}, Abs[x - y]}}, {300}];
ListVectorDensityPlot[data, VectorPoints -> 8,
ColorFunction -> "Pastel", VectorColorFunction -> Hue]
data = Table[{x, -y}, {x, -.5, 3, 0.2}, {y, -.5, 3, 0.2}];
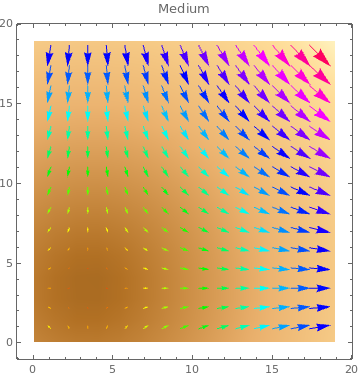
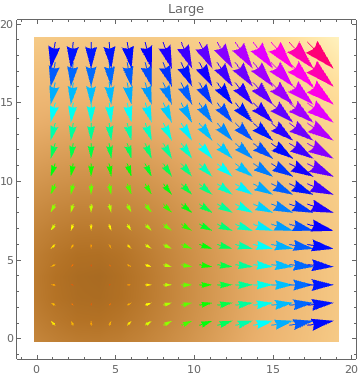
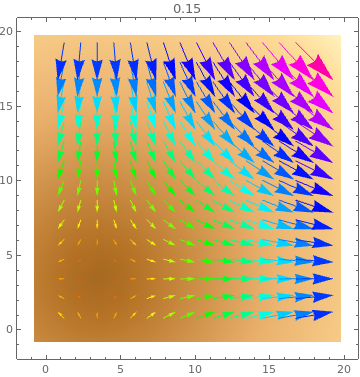
Table[ListVectorDensityPlot[data, VectorColorFunction -> Hue, PlotLabel -> s,
VectorScale -> s], {s, {Small, Medium, Large, 0.15}}]
data = Table[{-1 - x^2 + y, 1 + x - y^2}, {x, -3, 3, 0.2}, {y, -3, 3, 0.2}];
Table[ListVectorDensityPlot[data, PlotTheme -> k], {k, {"Marketing", "Detailed", "Business"}}]
data = Table[{1 + 2 x^2 + y, -1 - 3 x + 2 y^2}, {x, -3, 3, 0.2}, {y, -3, 3, 0.2}];
ListVectorDensityPlot[data, Mesh -> 5,
MeshFunctions -> Function[{x, y, vx, vy, n}, n]] ListVectorDensityPlot[data, Mesh -> 10,
MeshShading -> {Red, Yellow, Green, None}]
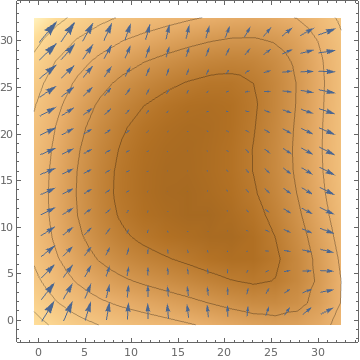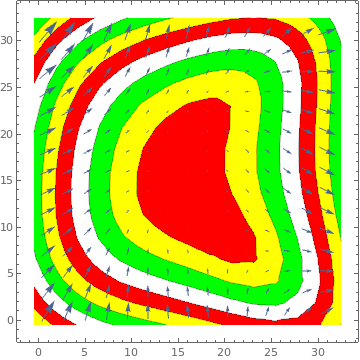data = Table[{-1 - 3 x^2 + 7 y, 1 - 4 x + 2 y^2}, {x, -3, 3, 0.2}, {y, -3, 3, 0.2}];
Table[ListVectorDensityPlot[data, Mesh -> 10,
MeshStyle -> s], {s, {Red, Thick, Directive[Red, Dashed]}}]
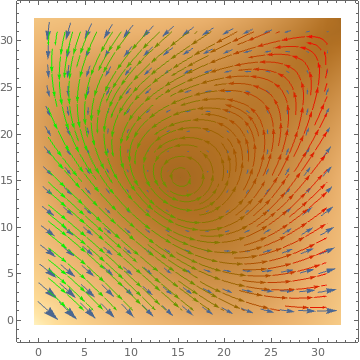
data = Table[{-1 + 2 x^2 - 7 y, 1 + 6 x - 2 y^2}, {x, -3, 3, 0.2}, {y, -3, 3, 0.2}];
ListVectorDensityPlot[data, StreamPoints -> Fine, StreamColorFunction ->
Function[{x, y, vx, vy, n}, Blend[{Green, Red}, x]]]

 

Return to Mathematica page
Return to the main page (APMA0330)
Return to the Part 1 (Plotting)
Return to the Part 2 (First Order ODEs)
Return to the Part 3 (Numerical Methods)
Return to the Part 4 (Second and Higher Order ODEs)
Return to the Part 5 (Series and Recurrences)
Return to the Part 6 (Laplace Transform)
Return to the Part 7 (Boundary Value Problems)