Preface

---

This section presents basic material about numerical solutions of parabolic equations.

Numerical Heat Solutions

---

We demonstrate application of finite difference schemes for numerical solution of the one-dimensional heat equation

where f(x) is a given function on the interval \( (0 , \ell ) . \) Usually, the boundary conditions are imposed on spacial variable x. For simplicity, we consider the boundary conditions of type I (called Dirichlet): where g₀ and g_l are specified temperatures at end points. As a rule, these functions are just constants. The heat equation models the temperature distribution in an insulated rod with ends held at constant temperatures g₀ and g_l when the initial temperature along the rod is known f. Although analytic solutions to the heat conduction equation can be obtained with Fourier series, we use the problem as a prototype of a parabolic equation for numerical solution.

Assume that the rectangle \( R= \{\,(x,t)\,:\, 0 \le x \le \ell , \ 0 \le t \le b \,\} \) is subdivided into n-1 and m-1 rectangles with sides Δx = h and Δt = k, as shown in the figure below.

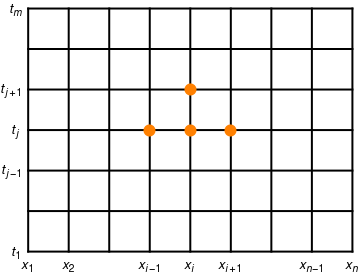
We are going to approximate the solution u(x,t) at grid points in successive rows \( \{ \,u(x_i , t)j )\,:\, i=1,2,\ldots , n \,\} \) for j=2,3,...,m. First, we approximate partial derivatives u_t and u_xx:

and The grid spacing is uniform in every row: x_i+1 = x_i + h and x_i-1 = x_i - h, and it is uniform in every column t_j+1 = t_j + k. Next, we drop the terms O(k) and O(h²) and use the approximation u_i,j for u(x_i, t_j) in the heat equation: which approximates the solution to the heat transfer equation. For convenience, the substitution is introduced, which leads to the explicit forward-difference equation This equation is used to create the (j+1)-th row across the grid, assuming that approximations in the j-th row are known. Notice that this formula explicitly gives the value u_i,j+1 in terms of u_i-1,j, u_i,j, and u_i+1,j. The corresponding computational stencil is represented below.

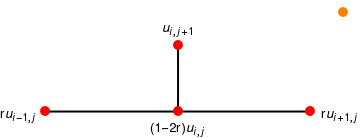
The simplicity of the above formula makes it appealing to use. However, it is important to utilize numerical techniques that are stable. If any error made at one stage of the calculations is eventually dampened out, the method is called stable. The above explicit forward-difference scheme is stable if and only if r is restricted to the interval \( 0 \le r \le \frac{1}{2} . \) This means that the step size k must satisfy so called the Courant--Friedrichs--Lewy or CFL condition: \( k \le h^2 /(2 \alpha^2 ) . \) The condition is named after Richard Courant (1888--1972), Kurt Friedrichs (1901--1982), and Hans Lewy (1904--1988) who described it in their 1928 paper. If the CFL condition is not fulfilled, errors committed in one line { u_i,j } might be magnified in subsequent lines { u_i,p } for some p > j. The next example illustrates this point.

Example: The forward-difference method is used to determine the solution of the heat equation

Program (Forward-difference method for the heat equation): to approximate the solution of \( u_t = \alpha^2 u_{xx} \) over \( R = \{\,(x,t) \,:\, 0 \le x \le \ell , \ 0 \le t \le b \) with u(x,0) = f(x), for 0 ≤ x ≤ ℓ, and u(0,t) = c₀, u(ℓ,t) = c_l, for 0 ≤ t ≤ b.

function U=forward(f,c0,cl,a,b,c,n,m)
% Input  -- f=u(x,0) as a string 'f'
%        -- c0=u(0,t) and cl=u(a,t)
%        -- a and b right end points of [0,a] and [0,b]
%        -- c=alpha^2 the thermal diffusivity in heat equation
%        -- n and m number of grid points over [0,a] and [0,b] 
% Output -- U solution matrix; 
% Initialize parameters and U
h=a/(n-1);
k=b/(m-1);
r=c*k/h^2;
s=1-2*r;
U=zeros(n,m);
% Boundary conditions
U(1,1:m)=c0;
U(n,1:m)=cl;
% Generate the first row
U(2:n-1,1)=feval(f,h:h:(n-2)*h)';
% Generate remaining rows of U
for j=2:m
    for j=2:n-1
        U(i,j)=s*U(i,j-1)+r*(U(i-1,j-1)+U(i+1,j-1));
    end
end
U=U';

 

 

An implicit finite difference scheme, invented in 1947 by John Crank (1916--2006) and Phyllis Nicholson (1917--1968), is based on numerical approximations for solutions of heat equation at the point (x,t+k/2) and that lies between the rows in the grid. Specifically, the approximation used for u_t(x,t+k/2) is obtained from the central-difference formula:

The approximation used for the second derivative u_xx(x,t+k/2) is the average of the approximations u_xx(x,t) and u_xx(x,t+k), which has an accuracy of the order O(h²): In a fashion similar to the previous derivation, we neglect the error terms O(k²) and O(h²) and substitute the remaining terms into the heat equation. Then employing the notation \( u_{i,j} = u(x_i , t_j ) \) will produce the finite difference scheme We also substitute \( r=\alpha^2 k/h^2 \) into the above formula. However, this time we must solve for the three "et to be computed" values u_i-1,j+1, u_i,j+1, and u_i+1,j+1. This is accomplished by placing them all on the left side of the equation. then rearrangement of the terms in the above difference equation results in the following Crank--Nicholson algorithm for i = 2,3,...,n-1. The terms on the right-hand side are all known. Hence the above equations form a tridiagonal linear system A X = B. Solving such tridiagonal systems was presented previously.

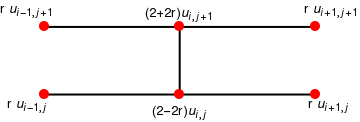
Program (Crank--Nicholson method for heat equation): to approximate the solution of \( u_t = \alpha^2 u_{xx} \) over \( R = \{\,(x,t) \,:\, 0 \le x \le \ell , \ 0 \le t \le b \) with u(x,0) = f(x), for 0 ≤ x ≤ ℓ, and u(0,t) = c₀, u(ℓ,t) = c_l, for 0 ≤ t ≤ b.

 
function U=crnich(f,c0,cl,a,b,c,n,m)
% Input  -- f=u(x,0) as a string 'f'
%        -- c0=u(0,t) and cl=u(a,t)
%        -- a and b right end points of [0,a] and [0,b]
%        -- c=alpha^2 the thermal diffusivity in heat equation
%        -- n and m number of grid points over [0,a] and [0,b] 
% Output -- U solution matrix; 
% Initialize parameters and U
h=a/(n-1);
k=b/(m-1);
r=c*k/h^2;
s1=2+2/r;
s2=2/r-2;
U=zeros(n,m);
% Boundary conditions
U(1,1:m)=c0;
U(n,1:m)=cl;
% Generate the first row
U(2:n-1,1)=feval(f,h:h:(n-2)*h)';
% Form the diagonal and off-diagonal elements of A and 
% the constant vector B and solve trigiagonal system AX=B
Vd(1,1:n)=s1*ones(1,n);
Vd(n)=1;
Vd(1)=1;
Va=-ones(1,n-1);
Va(n-1)=0;
Vc=-ones(1,n-1);
Vc(1)=0;
Vb(1)=c1;
Vb(n)=c2;
for j=2:m 
    for i=2:n-1
        Vb(i)=U(i-1,j-1)+U(i+1,j-1)+s2*U(i,j-1);
    end
    X=trisys(Va,Vd,Vc,Vb);
    U(1:n,j)=X';
end
U=U'

Example: The Crank--Nicholson method is used to determine the solution of the heat equation

 

 

 

 

Example: coupled Burgers equations

 

Example: coupled Newell--Whitehead--Segel equation

 

References

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions