Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part II of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

Planar Phase Portrait

Consider a systems of linear differential equations with constant coefficients

\begin{equation} \label{EqPhase.1} \dot{\bf x} = {\bf A}\,{\bf x} , \qquad\mbox{where} \quad \dot{\bf x} = {\text d}{\bf x}/{\text d}t , \end{equation}
and A is a square matrix. When matrix A in Eq.\eqref{EqPhase.1} is a 2×2 matrix and x(t) is a 2-dimensional column vector, this case is called planar, and we can take advatange of this to visualize the situation.

Since we know the structure of solutions to Eq.\eqref{EqPhase.1} from its fundamental matrix \( e^{{\bf A}\,t} , \) it is expected that the analysis of solutions near the origin is the most fruitful. It is not a surprise that this case requires a special attention.

An autonomous vector differential equation
\begin{equation} \label{EqPhase.2} \dot{\bf x} = {\bf f} ({\bf x}) , \qquad\mbox{where} \quad \dot{\bf x} = {\text d}{\bf x}/{\text d}t , \end{equation}
is said to have an equilibrium solution (also called stationary or critical point) x(t) = p if f(p) = 0. The critical point is called isolated if there is a neighborhood of the stationary point not containing another critical point.

Recall that a neighborhood of a point p is any set in ℝn that contains an open ball \( \| {\bf x} - {\bf p} \| = \sqrt{\left( x_1 - p_1 \right)^2 + \cdots +\left( x_n - p_n \right)^2 } < \varepsilon \) centered at p = [p1, …, pn]T. An equilibrium (also called stationary) solution of the autonomous system \eqref{EqPhase.2} is a point where the derivative of \( {\bf x}(t) \) is zero. An equilibrium solution is a constant solution of the system, and is usually called a critical point. For a linear system \( \dot{\bf x} = {\bf A}\,{\bf x}, \) an equilibrium solution occurs at each solution of the system (of homogeneous algebraic equations) \( {\bf A}\,{\bf x} = {\bf 0} . \) As we have seen, such a system has exactly one solution, located at the origin, if \( \det{\bf A} \ne 0 .\) If \( \det{\bf A} = 0 , \) then there are infinitely many solutions, and the critical point is not isolated.

Previously, we used a direction (or tangent) field to depict the behavior of solutions without actual solving the differential equation. Now we are going to enhance its features by adding arrows to accommodate time presence and plot some typical solutions. The accurate tracing of the parametric curves of the solutions is not an easy task without computers. However, we can obtain a very reasonable approximation of a trajectory by using the very same idea behind the slope field, namely the tangent line approximation.

The phase portrait of Eq.\eqref{EqPhase.1} or in general, \eqref{EqPhase.2}, is a geometric representation of the trajectories of a dynamical system in the phase plane. The phase portrait contains some typical solution curves along with arrows indicating time variance of solutions (from corresponding direction field) and possible separatrices (if any).
Recall that a separatrix is the boundary separating two modes of behaviour in a differential equation and not every dynamoc system has a separatrix. A sketch of a particular solution in the phase plane is called the trajectory or orbit or streamline of the solution. Solutions of Eq.\eqref{EqPhase.1} are plotted as parametric curves (with t as the parameter) on the Cartesian plane tracing the path of each particular solution \( {\bf x} = \left[ x_1 (t) , x_2 (t) \right]^{\mathrm T} , \ -\infty < t < \infty . \) Similar to a direction field for a single differential equation, a phase portrait is a graphical tool to visualize how the solutions of a given system of differential equations would behave in a neighborhood of the critical point.

We will classify the critical points of various systems of first order linear differential equations by their stability. Since the general treatment of stability and instability is given in Part III of this tutorial, it is reasonable to provide its descriptive definition.

A critical point is called an attractor or sink if every solution in a proximity of it moves toward to the stationary point (so it converges to the critical point) as t → +∞. Alternatively, if trajectories near a stationary point leave it as t → +∞, then the critical point is referred to as the repeller or source.
Remember that solutions to constant coefficient linear system of differential equations exist for all t ∈ (−∞, ∞). Since the independent variable t is associated with time (which in reality is not invertible), we are mostly interested in understanding the behavior of solutions when t → +∞. However, an attractor becomes a repeller when you consider t → −∞ and vice versa. Each set of initial conditions is represented by a different curve, or point. They consist of a plot of typical trajectories in the state space. This reveals information such as whether a critical point is an attractor, or a repeller or limit cycle is present for the chosen parameter value.

In addition, due to the truly two-dimensional nature of the parametric curves, we will also classify the type of those critical points based on the behavior of solutions near equilibria (or, rather, by the shape formed by the trajectories about each critical point).

In our study of phase portraits and critical points, we will encounter four types of critical points: nodes, saddle point, spiral, and center. Note that this is typical only for two-dimensional problems. Additionally, these critical points are based on the eigenvalues and eigenvectors of the constant coefficient linear system of differential equations. The table below emphasizes the relationship between the stability and type of critical point based on the eigenvalues.

 

Singular Matrices

If a square matrix is singular, then at least one of its eigenvalues is zero. In this case, the origin is not an isolated critical point and there is a line of stationary points. This line is an eigenspace corresponding to the zero eigenvalue and it is also a separatrix in the phase portrait.

Example 1: Consider the 2×2 matrix

\[ {\bf A} = \begin{bmatrix} 1&2 \\ 2& 4 \end{bmatrix} . \]
It has two eigenvalues
A = {{1, 2}, {2, 4}}
Eigenvalues[A]
{5, 0}
Then we find the corresponding eigenvectors:
Eigenvectors[A]
{{1, 2}, {-2, 1}}
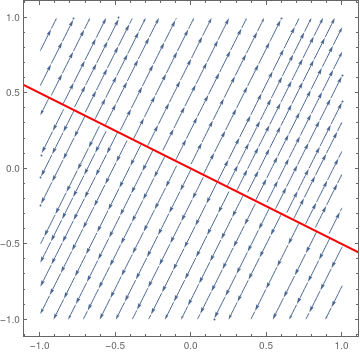
      So we know that the eigenvalue λ = 0 has a corresponding eigenvector [−2, 1]. Then we plot the direction field along with the separatrix corresponding to the eigenspace of λ = 0.
sp = StreamPlot[{x + 2*y, 2*x + 4*y}, {x, -1, 1}, {y, -1, 1}];
line = Graphics[{Thick, Red, Line[{{-2, 1}, {2, -1}}]}];
Show[sp, line]
       Separatrix is an example of non-isolated equilibria.            Mathematica code

   ■

Isolated Equilibria

As a rule, we will only consider systems of linear differential equations whose coefficient matrix A has a nonzero determinant.

In two-dimensional space, it is possible to completely classify the critical points of various systems of first order linear differential equations by their stability. In addition, due to the truly two-dimensional nature of the parametric curves, we will also classify the type of those critical points by their shapes (or, rather, by the shape formed by the trajectories about each critical point). Their classification is based on eigenvalues of the coefficient matrix. Therefore, we consider different cases.

There are four types of critical points. To characterize them, it is convenient to use polar coordinates. Suppose that the solution curve of the autonomous planar differential equation dx/dt = f(x) can be written as x = x(t), y = y(t), where x = [x(t), y(t)]T is a two-dimensional column vector. Then in polar coordinates, their trajectory can be written as

\begin{equation} \label{EqPhase.3} r = \rho (t) \ge 0, \qquad \theta = \omega (t) , \end{equation}
with x(t) = ρ(t) cosω(t),         y(t) = ρ(t) sinω(t). For matrix \( {\bf A} = \begin{bmatrix} a & b \\ c& d \end{bmatrix} , \) the polar variables satisfy the equations:
\begin{equation} \label{EqPhase.4} \dot{r} = r \left[ a\,\cos^2 \theta + \left( b+c \right) \cos\theta\,\sin\theta + d\,\sin^2 \theta \right] , \qquad \dot{\theta} = c\,\cos^2 \theta + \left( d-a \right) \cos\theta\,\sin \theta -b\,\sin^2 \theta . \end{equation}

 

Nodes

A critical point (0,0) of the constant coefficient autonomous equation \eqref{EqPhase.1} is said to be a node if \( \lim_{t\to +\infty} \left\vert \omega (t) \right\vert = \) constant or \( \lim_{t\to -\infty} \left\vert \omega (t) \right\vert = \) constant, when x(t) belongs to some neighborhood of the critical point. In the former case, the critical point is called nodal sink, and in latter, it is a nodal source.
Nodes are critical points with the property that a trajectories arrive or depart from the critical point along some directory. In turn, there are known of three types of nodes:
An equilibrium solution of an autonomous system of differential equations \( \dot{\bf x} = {\bf f}\left( {\bf x}\right) \) is called a node if nearby trajectories approach it or depart from the critical point along some definite direction (semi-straight line). Correspondingly, the critical point is referred to as nodal sink or nodal source, depending whether trajectories approach the stationary point or depart from it as t → +∞.
The trajectories that are the eigenvectors move in straight lines. The rest of the trajectories move, initially when near the critical point, roughly in the same direction as the eigenvector of the eigenvalue with the smaller absolute value. Then, farther away, they would bend toward the direction of the eigenvector of the eigenvalue with the larger absolute value.

For constant coefficient linear differential equations, classification of critical points can be performed based on eigenvalues of the corresponding constant matrix.

Case 1: Diagonal real-valued matrix with the same entries and of the same sign. A proper node can be observed only when the matrix of the system is a constant real multiple of the diagonal matrix:

\[ \alpha \, \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} = \begin{bmatrix} \alpha &0 \\ 0&\alpha \end{bmatrix} \quad \mbox{ where } \alpha \quad \mbox{is an arbitrary nonzero constant} . \]
In this case, the system is uncoupled and each equation can be solved separately. Numbers on the diagonal are eigenvalues of the matrix. See the following example. Then the general solution is
\[ {\bf y}(t) = \begin{bmatrix} y_1 (t) \\ y_2 (t) \end{bmatrix} = c_1 \begin{bmatrix} \xi \\ 0 \end{bmatrix} e^{\lambda\,t} + c_2 \begin{bmatrix} 0 \\ \eta \end{bmatrix} e^{\lambda\,t} , \]
with arbitrary constants c1 and c2.

Example 2: Consider the following 2×2 matrices

\[ {\bf A}_1 = \begin{bmatrix} 1&0 \\ 0& 1 \end{bmatrix} , \qquad {\bf A}_2 = \begin{bmatrix} -1&\phantom{-}0 \\ \phantom{-}0& -1 \end{bmatrix} . \]
Upon plotting the corresponding phase portraits, we see that matrix A1 generate proper nodal source at the origin, whereas matrix A2 corresponds to proper nodal sink.
StreamPlot[{x, y}, {x, -1, 1}, {y, -1, 1}, ClippingStyle -> {Blue, Red}]
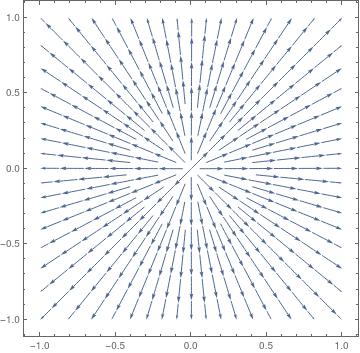
VectorPlot[{x, 2*y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific"]
StreamPlot[{-x, -y}, {x, -1, 1}, {y, -1, 1}, StreamPoints -> 30]
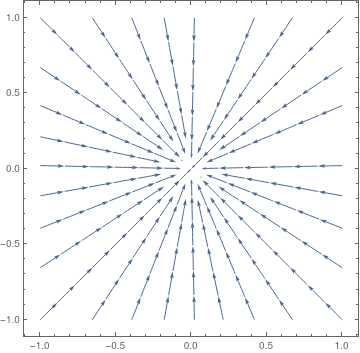
VectorPlot[{-x, -2*y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Web"]
           
Figure 2: Proper nodal source, matrix A1.           Figure 3: Proper nodal sink, matrix A2.
   ■

Case 2: Distinct real eigenvalues of the same sign. Then the general solution of the linear system \( \dot{\bf x} = {\bf A}\,{\bf x}, \) is

\[ {\bf x} (t) = c_1 \,{\bf \xi} \, e^{\lambda_1 t} + c_2 \,{\bf \eta} \, e^{\lambda_2 t} , \]

where \( \lambda_1 \) and \( \lambda_2 \) are distinct real eigenvalues, \( {\bf \xi} \) and \( {\bf \eta} \) are corresponding eigenvectors, and \( c_1 , c_2 \) are arbitrary real constants.

When eigenvalues λ1 and λ2 are both positive, or are both negative, the phase portrait shows trajectories either moving away from the critical point toways infinity (for positive eigenvalues), or moving directly towards and converging to the critical point (for negative eigenvalues). The trajectories that are the eigenvectors move in straight lines. The rest of the trajectories move, initially when near the critical point, roughly in the same direction as the eigenvector of the eigenvalue with the smaller absolute value. Then, farther away, they would bend toward the direction of the eigenvector of the eigenvalue with the larger absolute value. This type of critical point is called a node. It is asymptotically stable if eigenvalues are both negative, unstable if eigenvalues are both positive.

Stability: It is unstable if both eigenvalues are positive; asymptotically stable if they are both negative.

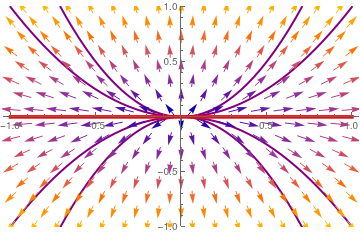
Example 3: We start with the diagonal matrix and corresponding autonomous differential equation

\[ {\bf B} = \begin{bmatrix} 1&0 \\ 0&2 \end{bmatrix} , \qquad \frac{{\text d}{\bf y}}{{\text d}t} = {\bf B} \,{\bf y}(t) . \]
So the given system is decoupled
\[ \dot{x} = x , \qquad \dot{y} = 2\,y , \]
with the general solution
\[ {\bf y}(t) = \begin{bmatrix} x(t) \\ y(t) \end{bmatrix} = c_1 \begin{bmatrix} 1 \\ 0 \end{bmatrix} e^{t} + c_2 \begin{bmatrix} 0 \\ 1 \end{bmatrix} e^{2t} . \]
Here, c1 and c2 are arbitrary constants. We can find the explicit solution from the equation
\[ \frac{{\text d}y}{{\text d}x} = \frac{\dot{y}}{\dot{x}} = \frac{2y}{x} \qquad \Longrightarrow \qquad y = x^2 . \]
      We plot the direction field along with some trajectories and separatrix y = 0. Another eigenspace x = 0 (vertical line) is not actually a separatrix, and it is not shown.
vp = VectorPlot[{x, 2*y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific"];
tb = Plot[Table[c*x^2, {c, -2, 2}], {x, -1, 1}, PlotStyle -> {Thick, Purple}, PlotRange -> {-1, 1}];
line = Graphics[{Red, Thickness[0.01], Line[{{-1, 0}, {1, 0}}]}];
Show[tb, vp, line]

     Mathematica code.
       Separatrix y = 0 (in red) and phase portrait for matrix B. The origin is a nodal source---repeller.            

For another diagonal matrix
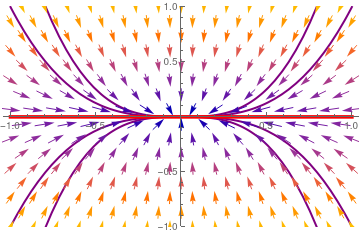
\[ {\bf B}_2 = \begin{bmatrix} -1&\phantom{-}0 \\ \phantom{-}0&-3 \end{bmatrix} , \qquad \frac{{\text d}{\bf y}}{{\text d}t} = {\bf B}_2 \,{\bf y}(t) . \]
we have a similar phase portrait, but the origin becomes nodal sink.
      Upon separation of variables, we obtain its general solution
\[ \frac{{\text d}y}{{\text d}x} = \frac{\dot{y}}{\dot{x}} = \frac{-3y}{-x} \qquad \Longrightarrow \qquad y = x^3 . \]
We plot the direction field along with some trajectories and separatrix y = 0
vp = VectorPlot[{-x, -3*y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific"];
tb = Plot[Table[c*x^2, {c, -2, 2}], {x, -1, 1}, PlotStyle -> {Thick, Purple}, PlotRange -> {-1, 1}];
line = Graphics[{Red, Thickness[0.01], Line[{{-1, 0}, {1, 0}}]}];
Show[tb, vp, line]
       Separatrix y = 0 (in red) and phase portrait for matrix B2. The origin is a nodal sink (attractor).            Mathematica code

   ■
An example of a stable node is provided by the overdamped oscillator: \( \ddot{x} + 3\dot{x} + x = 0 . \)

Example 4: Consider two matrices

\[ {\bf A}_1 = \begin{bmatrix} -5&2 \\ -4&1 \end{bmatrix} , \qquad {\bf A}_2 = \begin{bmatrix} 2&1 \\ 1&2 \end{bmatrix} \]
A1 = {{-5, 2}, {-4, 1}}
Eigenvalues[A1]
{-3, -1}
This tells us that the origin is the attractor because both eigenvalues are real negative numbers.
Eigenvectors[A1]
{{1, 1}, {1, 2}}
So we know that separatrix is going along each eigenvector corresponding to distinct eigenvalues. We plot the corresponding eigenlines; one of them corresponding to the largest absolute value (λ = −3) is indicated by double arrow and another eigenline (λ = −1) is labeled by a single arrow.
arr1 = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{1, 1}, {0, 0}}]}];
arr1a = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{1, 1}, {0.1, 0.1}}]}];
arr2 = Graphics[{Purple, Thick, Arrowheads[0.06], Arrow[0.5*{{1, 2}, {0.2, 0.4}}]}];
arr4 = Graphics[{Purple, Thick, Arrowheads[0.06], Arrow[0.5*{{-1, -2}, {-0.2, -0.4}}]}];
arr3 = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{-1, -1}, {0, 0}}]}];
arr3a = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{-1, -1}, {-0.1, -0.1}}]}];
sp = StreamPlot[{-5*x + 2*y, -4*x + y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific", StreamStyle -> Blue];
Show[arr1, arr1a, arr2, arr3, arr3a, arr4, sp]

Now we perform a similar job with another matrix A2.

A2 = {{2, 1}, {1, 2}}
Eigenvalues[A2]
{3, 1}
This tells us that the origin is a repeller because both eigenvalues are real positive numbers.
Eigenvectors[A2]
{{1, 1}, {-1, 1}}
vp = VectorPlot[{2*x + y, x + 2*y}, {x, -1, 1}, {y, -1, 1}, StreamStyle -> Blue];
arr1 = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {1, 1}}]}];
arr1a = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {0.9, 0.9}}]}];
arr2 = Graphics[{Orange, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {-1, 1}}]}];
arr4 = Graphics[{Orange, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {1, -1}}]}];
arr3 = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {-1, -1}}]}];
arr3a = Graphics[{Red, Thick, Arrowheads[0.06], Arrow[{{0, 0}, {-0.9, -0.9}}]}];
Show[arr1, arr1a, arr2, arr3, arr3a, arr4, vp]
The graphs below show phase portrait around the critical point (origin) along with separatricies that go along eigenlines (generated by eigenvectors). The eigenline corresponding to the dominant eigenvalue (having largest absolute value) is shown with double arrow and red color.
     
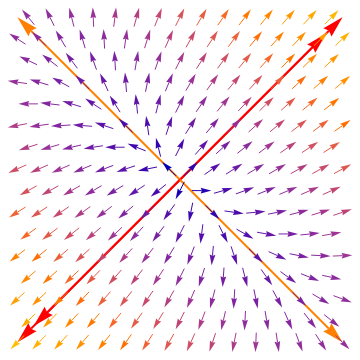
Figure 6: Improper nodal source with dominated separatrix labeled by double arrow.       Figure 7: Improper nodal sink.
   ■

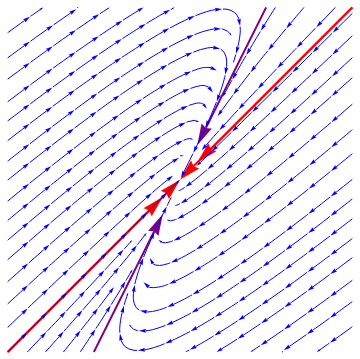
Case 3: Repeated real eigenvalue with one eigenvector. If a square 2×2 matrix is not diagonal and has a defective (repeated) eigenvalue, then the matrix has only one eigenvector. It is not diagonalizable and its general solution is of the form

\[ {\bf x} (t) = e^{{\bf A}t} {\bf c} = c_1 \,{\bf \xi} \, e^{\lambda\, t} + c_2 \,e^{\lambda\, t} \left( t\,{\bf \xi} + {\bf \eta} \right) , \]
where ξ is the eigenvector and η is so called the generalized eigenvector. The original is the degenerate node, either attractor if its eigenvalue is negative, or repeller if its eigenvalue is positive. The trajectories either all diverge away from the critical point towards infinity (when eigenvalue λ > 0) or all converge towards the critical point (when eigenvalue λ < 0). This type of critical point is called an improper node. It is asymptotically stable if \( \lambda <0 ,\) unstable if \( \lambda >0 .\) The phase portrait is presented in the following example.

Example 5: Consider two matrices

\[ {\bf A}_3 = \begin{bmatrix} 5&-3 \\ 3& -1 \end{bmatrix} , \qquad {\bf A}_4 = \begin{bmatrix} -5&-3 \\ \phantom{-}3&\phantom{-}1 \end{bmatrix} . \]
Using Mathematica, we determine that matrix A3 has one defective eigenvalue λ = 2; this tells us that the origin is the repeller.
A3 = {{5, -3}, {3, -1}};
Eigenvalues[A3]
{2, 2}
Eigenvectors[A3]
{{1, 1}, {0, 0}}
We plot the direction field and the separatrix (in red) that is spanned on the eigenvectors.
vp = VectorPlot[{5*x - 3*y, 3*x - y}, {x, -1, 1}, {y, -1, 1}, StreamStyle -> Blue];
line = Graphics[{Red, Thick, Line[{{-1, -1}, {1, 1}}]}];
Show[line, vp]
Then we repeat the same job for matrix A4.
A4 = {{-5, -3}, {3, 1}};
Eigenvalues[A3]
{-2, -2}
Eigenvectors[A4]
{{-1, 1}, {0, 0}}
sp = StreamPlot[{-5*x - 3*y, 3*x + y}, {x, -1, 1}, {y, -1, 1}, StreamStyle -> Blue];
line = Graphics[{Red, Thickness[0.01], Line[{{-1, 1}, {1, -1}}]}];
Show[line, sp]
     
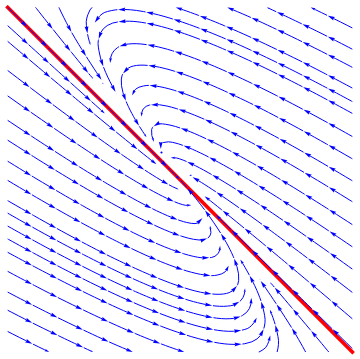
Figure 8: Degenerate nodal source.       Figure 9: Degenerate nodal sink.
   ■

 

Saddle points

A critical point (0,0) of the constant coefficient autonomous equation \eqref{EqPhase.1} is said to be a saddle point if there are two trajectories approaching the origin along opposite directions, and all other orbits close to either of them and to (0,0) tend away from them as t becomes infinite.

Case 4: Distinct real eigenvalues are of opposite signs. In this type of phase portrait, the trajectories given by the eigenvectors of the negative eigenvalue initially start at infinity before moving towards and eventually converging at the critical point. The trajectories that represent the eigenvectors of the positive eigenvalue move in exactly the opposite way: starting at the critical point before diverging to infinity. Every other trajectory starts at infinity, moves toward but never converges to the critical point, and then changes direction and moves back towards infinity. All the while it would roughly follow the 2 sets of eigenvectors. This type of critical point is called a saddle point. It is always unstable.

Stability: It is always unstable.

Example 6: Consider a system of ordinary differential equations

\[ \frac{{\text d}}{{\text d} t} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1&2 \\ 2&1 \end{bmatrix} \, \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} . \]
We can enter this equation into Mathematica either as a vector
f[x_, y_] = {x + 2*y, 2*x + y}; Print["X' = ", MatrixForm[f[x, y]]]
\( X' = \begin{pmatrix} x+2\,y\\ 2\,x +y \end{pmatrix} \)
or as two equations
Print["x' = ", f[x, y][[1]], ", y' = ", f[x, y][[2]]]
\( x' = x + 2\,y, \quad y' = 2\,x + y \)

The coefficient matrix \( {\bf A} = \begin{bmatrix} 1&2 \\ 2&1 \end{bmatrix} \) has two distinct real eigenvalues \( \lambda_1 =3 \) and \( \lambda_2 =-1 . \) Therefore, the critical point, which is the origin, is a saddle point, unstable. We plot the corresponding phase portrait using the following codes. Mathematica provides us at least two options: either StreamPlot or VectorPlot (for the latter we give two versions without normalization and with it).

splot = StreamPlot[{x + 2*y, 2*x + y}, {x, -4, 4}, {y, -3, 3}, StreamColorFunction -> "Rainbow"];
Manipulate[ Show[splot, ParametricPlot[ Evaluate[ First[{x[t], y[t]} /.
NDSolve[{x'[t] == x[t] + 2*y[t], y'[t] == 2*x[t] + y[t], Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0, T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}}, Locator}, SaveDefinitions -> True]
and the phase portrait with VectorPlot
Show[VectorPlot[f[x, y], {x, -4, 4}, {y, -4, 4}], Frame -> True, BaseStyle -> {FontFamily -> "Times", FontSize -> 14}]
Show[VectorPlot[f[x, y]/Norm[f[x, y]], {x, -4, 4}, {y, -4, 4}], Frame -> True, BaseStyle -> {FontFamily -> "Times", FontSize -> 14}]
   StreamPlot    VectorPlot    VectorPlot with normalization
       
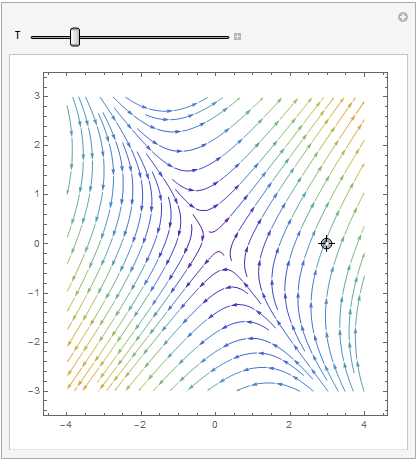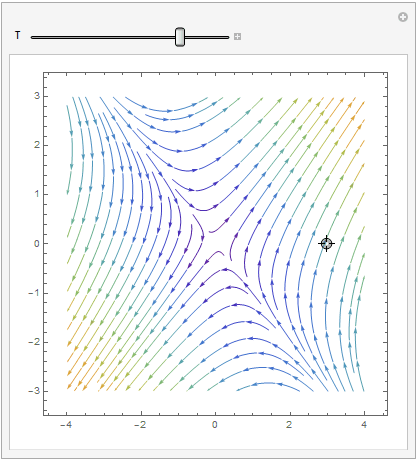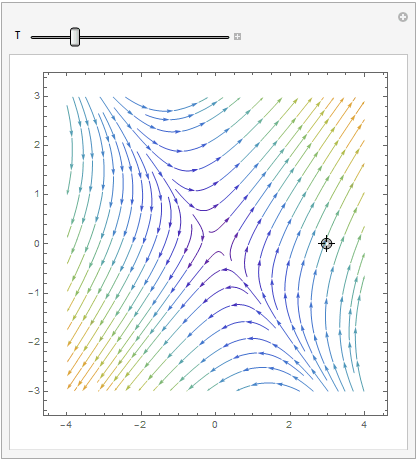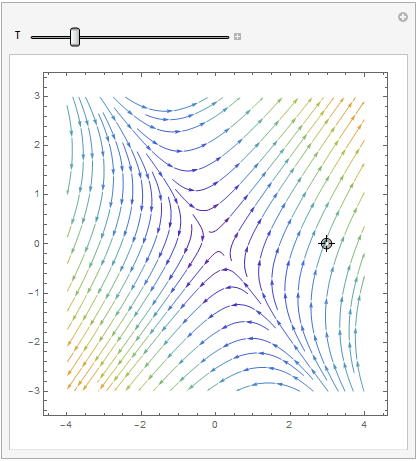
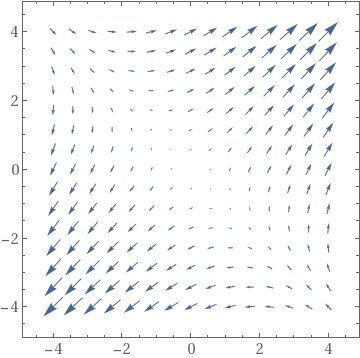
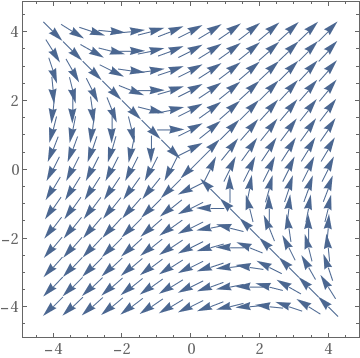
It is clear that the origin is an unstable equilibrium solution.    ■

 

 

Spiral points

A critical point (0,0) of the constant coefficient autonomous equation \eqref{EqPhase.1} is said to be a spiral point if the following three conditions hold for all orbits in some neighbohood of the origin.
  • all trajectories are defined on t0 < t < ∞ or −∞ < t < t0 for some t0;
  • \( \lim_{t\to +\infty} r (t) = 0 \) or \( \lim_{t\to -\infty} r (t) = 0 . \)
  • \( \lim_{t\to +\infty} \left\vert \omega (t) \right\vert = \infty \) or \( \lim_{t\to -\infty} \left\vert \omega (t) \right\vert = \infty . \)

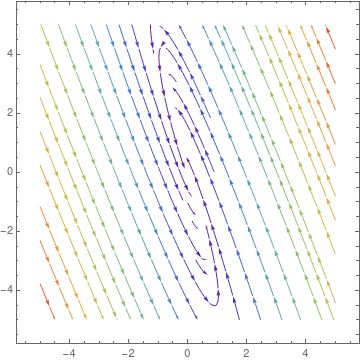
Case 5: Complex conjugate eigenvalues. When the real part of eigenvalues is nonzero, the trajectories still retain the elliptical traces. However, with each revolution, their distances from the critical point grow/decay exponentially according to the term \( e^{\Re\lambda\,t} , \) where \( \Re\lambda \) is the real part of the complex λ, the eigenvalue. Therefore, the phase portrait shows trajectories that spiral away from the critical point toways infinity (when \( \Re\lambda > 0 \) ), or trajectories that spiral toward, and converge to the critical point (when \( \Re\lambda < 0 \) ). This type of critical point is called a spiral point. It is asymptotically stable if \( \Re\lambda < 0 ,\) it is unstable if \( \Re\lambda > 0 . \)

An example of a stable spiral is provided by the underdamped oscillator: \( \ddot{x} + \dot{x} + x = 0 . \)

Example 7: Consider two matrices

\[ {\bf A}_5 = \begin{bmatrix} -1&13 \\ -1& \phantom{1}3 \end{bmatrix} , \qquad {\bf A}_6 = \begin{bmatrix} -3&13 \\ -1&\phantom{3}1 \end{bmatrix} . \]
The eigenvalues of both matrices are complex conjugate numbers:
A5 = {{-1, 13}, {-1, 3}}; Eigenvalues[A5]
{1 + 3 I, 1 - 3 I}
and
A6 = {{-3, 13}, {-1, 1}}; Eigenvalues[A6]
{-1 + 3 I, -1 - 3 I}
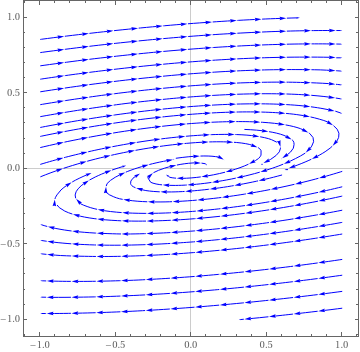
      We plot the direction field in a neighborhood of the asymptotically stable stationary point. Note that trajectories approach the origin in clockwise direction.
StreamPlot[{-3*x + 13*y, -x + y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
       Spiral critical point for matrix A6.            Mathematica code

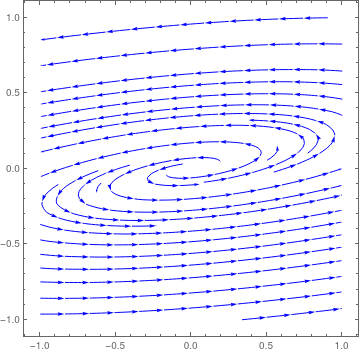
      We plot the direction field in a neighborhood of the asymptotically stable stationary point for matrix −A6. Note that trajectories approach the origin in counterclockwise direction.
StreamPlot[{3*x - 13*y, x - y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Detailed", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
       Spiral asymptotically stable critical point for matrix −A6.            Mathematica code

Now we do a similar job for matrix A5 that has unstable critical point at the origin.
      We plot the direction field in a neighborhood of the ustable stationary point. Note that trajectories depart from the origin in clockwise direction.
StreamPlot[{-x + 13*y, -x + 3*y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Minimal", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
       Spiral unstable critical point for matrix A5.            Mathematica code

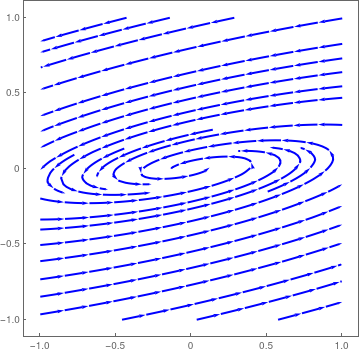
      We plot the direction field in a neighborhood of the unstable stationary point for matrix −A5. Note that trajectories depart from the origin in counterclockwise direction.
StreamPlot[{x - 13*y, x - 3*y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Web", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
       Spiral unstable critical point for matrix −A5.            Mathematica code

   ■

 

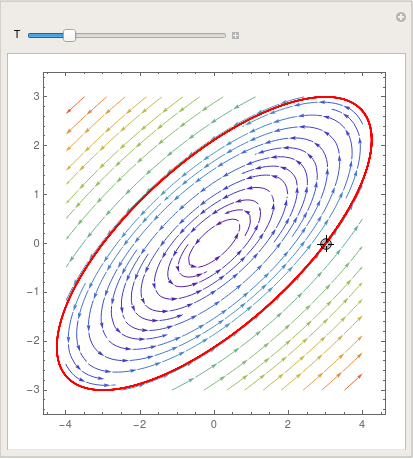
Center

A critical point (0,0) of the constant coefficient autonomous equation \eqref{EqPhase.1} is said to be a center if there exists a neighborhood containing countably many closed trajectories, each containing the origin and diameters tend to zero.

Case 6: Two pure complex conjugate eigenvalues. When the real part of the eigenvalues is zero, the trajectories neither converge to the critical point nor move toways infinitey. Rather, they stay in constant, elliptical (or, rarely, circular) orbits. This type of critical point is called a center. It has a unique stability classification shared by no other: stable (or neutrally stable).

An example of a center is provided by the simple harmonic oscillator: \( \ddot{x} + x = 0 . \)

Example 8: Consider the system of differential equations

\[ \frac{{\text d}{\bf x}}{{\text d}t} \equiv \frac{\text d}{{\text d}t} \begin{bmatrix} x(t) \\ y(t) \end{bmatrix} = \begin{bmatrix} x-y \\ 5x-y \end{bmatrix} . \]
The corresponding matrix
\[ {\bf A} = \begin{bmatrix} 1&-1 \\ 5&-1 \end{bmatrix} \]
has two complex conjugate pure imaginary eigenvalues
B = {{1, -1}, {5, -1}}; Eigenvalues[B]
{2 I, -2 I}
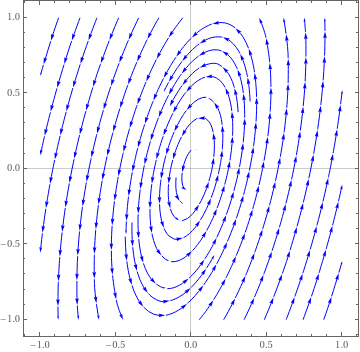
      We plot the direction field.
StreamPlot[{x -y, 5*x - y}, {x, -1, 1}, {y, -1, 1}, PlotTheme -> "Scientific", StreamStyle -> Blue, PerformanceGoal -> "Quality", StreamPoints -> 25]
       Center critical point.            Mathematica code

   ■
Eigenvalues Condition Type of Critical Point Stability
λ1 > λ2 > 0 tr(A) > 0 and tr²(A) > 4 det(A), det(A) > 0 Nodal source (node) Unstable
λ1 < λ2 < 0 tr(A) < 0 and tr²(A) > 4 det(A), det(A) > 0 Nodal sink (node) Asymptotically stable
λ1 < 0 < λ2 detA < 0 Saddle point Unstable
λ1 = λ2 > 0
diagonal matrix		 A = k I with k>0 Proper node (star) Unstable
λ1 = λ2 < 0
diagonal matrix 		A = k I with k<0 Proper node (star) Asymptotically stable
λ1 = λ2 > 0
missing eigenvector		 A = k1 I + k2 I with k>0 Improper/degenerate node Unstable
λ1 = λ2 < 0
missing eigenvalue 		A = k1 I + k2 I with k<0 Improper/degenerate node Asymptotically stable
λ = α ± jβ,     α > 0 tr(A) > 0 and tr²(A) < 4 det(A) Spiral point Unstable
λ = α ± jβ,     α < 0 tr(A) < 0 and tr²(A) < 4 det(A) Spiral point Asymptotically stable
λ = ± jβ tr(A) = 0 and tr²(A) < 4 det(A) Center Stable

 

Mathematica plots phase portraits

Mathematica gives several options to plot phase portraits for planar systems of differential equations. We show them by examples. Matrix

\[ \begin{bmatrix} 13&4 \\ 4&7 \end{bmatrix} \]
has two positive distinct eigenvalues
c = {{13, 4}, {4, 7}};
Eigenvalues[c]
{15, 5}
Eigenvectors[c]
{{2, 1}, {-1, 2}}
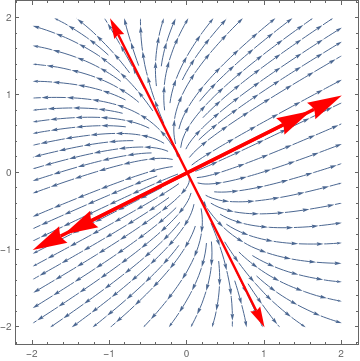
      Then we plot direction field and two separatrices using StreamPlot
ar1 = Graphics[{Red, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {2, 1}}]}];
ar1a = Graphics[{Red, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {1, 0.5}*1.6}]}];
ar2 = Graphics[{Red, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {-2, -1}}]}];
ar2a = Graphics[{Red, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {-1, -0.5}*1.6}]}];
ar3 = Graphics[{Red, Thickness[0.007], Arrowheads[0.06], Arrow[{{0, 0}, {-1, 2}}]}];
ar3a = Graphics[{Red, Thickness[0.007], Arrowheads[0.06], Arrow[{{0, 0}, {1, -2}}]}];
sp = StreamPlot[{13 x + 4 y, 4 x + 7 y}, {x, -2, 2}, {y, -2, 2}];
Show[sp, ar1, ar1a, ar2, ar2a, ar3, ar3a]
       Nodal repeller and two separatreces.            Mathematica code

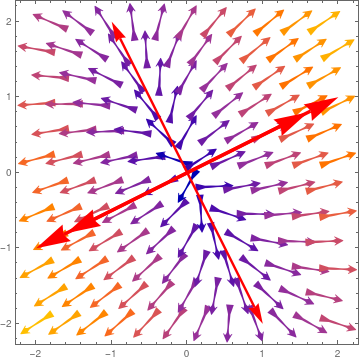
      Then we plot the direction field with VectorPlot command. As usual, the dominated eigenspace is identified with double arrow.
ar1 = Graphics[{Red, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {2, 1}}]}];
ar1a = Graphics[{Red, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {1, 0.5}*1.6}]}];
ar2 = Graphics[{Red, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {-2, -1}}]}];
ar2a = Graphics[{Red, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {-1, -0.5}*1.6}]}];
ar3 = Graphics[{Red, Thickness[0.007], Arrowheads[0.06], Arrow[{{0, 0}, {-1, 2}}]}];
ar3a = Graphics[{Red, Thickness[0.007], Arrowheads[0.06], Arrow[{{0, 0}, {1, -2}}]}];
vp = VectorPlot[{13 x + 4 y, 4 x + 7 y}, {x, -2, 2}, {y, -2, 2}, VectorScale -> 0.1, VectorPoints -> 12, VectorStyle -> "Dart"];
Show[vp, ar1, ar1a, ar2, ar2a, ar3, ar3a]
       Two Separatrices divide the phase plane into four parts.            Mathematica code

 

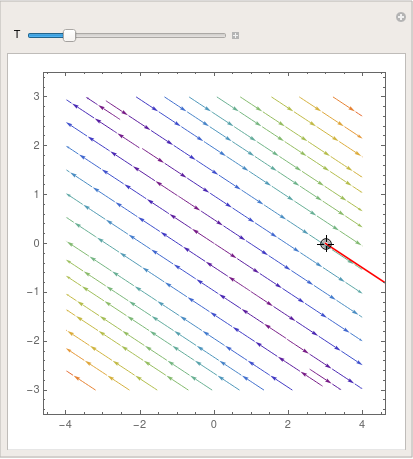
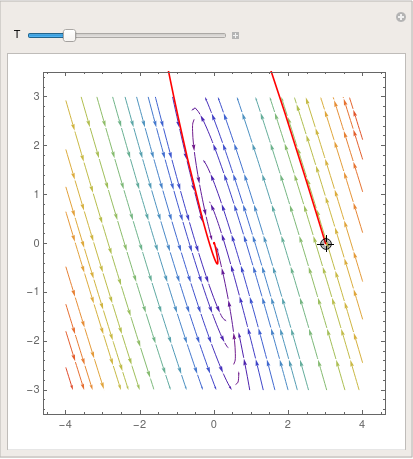
We can take advantage of the Manipulate command that allows one to change
(in our case) the initial point along with the direction field:

 

     
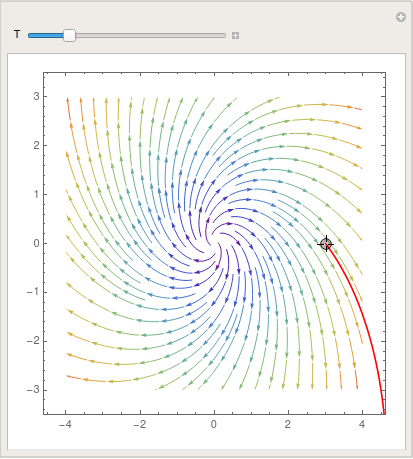
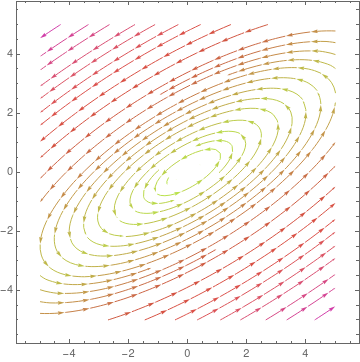
parta = StreamPlot[{x + y, y - x}, {x, -4, 4}, {y, -3, 3},
StreamColorFunction -> "Rainbow"];
Manipulate[
Show[parta,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == x[t] + y[t], y'[t] == y[t] - x[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
       Demonstration of Manipulate command.            Mathematica code

To save the image, use Mathematica command Export:

Export["foo.gif",%]

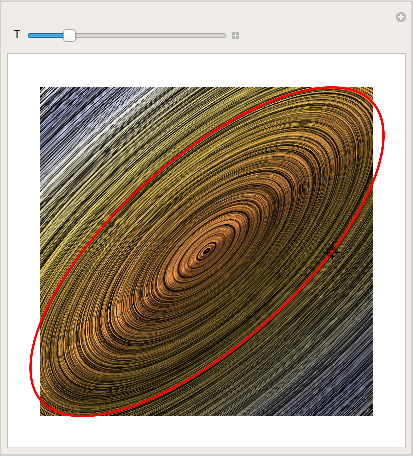
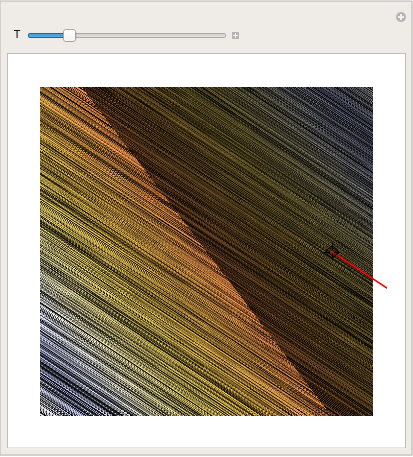
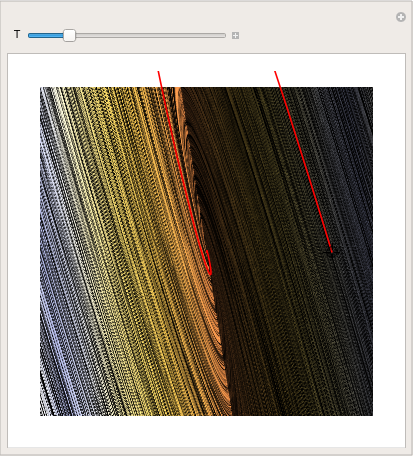
You can even make a cool picture by using LineIntegralConvolutionPlot:

     
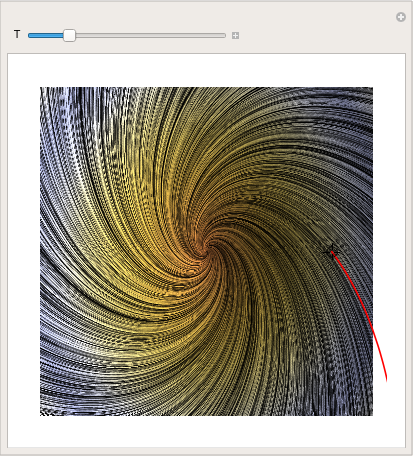
parta = LineIntegralConvolutionPlot[{{x + y, y - x}, {"noise", 1000,
1000}}, {x, -4, 4}, {y, -3, 3}, ColorFunction -> "BeachColors",
LightingAngle -> 0, LineIntegralConvolutionScale -> 3,
Frame -> False];
Manipulate[
Show[parta,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == x[t] + y[t], y'[t] == y[t] - x[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
       Demonstration of LineIntegralConvolutionPlot command.            Mathematica code


To put three colors into the plot, one may use

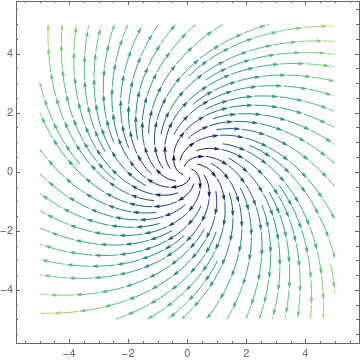
StreamPlot[{x + y, y - x}, {x, -5, 5}, {y, -5, 5}, StreamColorFunction -> "BlueGreenYellow"]

partb = StreamPlot[{x - 2*y, x - y}, {x, -4, 4}, {y, -3, 3},
StreamColorFunction -> "Rainbow"];
Manipulate[
Show[partb,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == x[t] - 2*y[t], y'[t] == -y[t] + x[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]

To save the image as gif-file, type:

Export["foo.gif",%]
partb = LineIntegralConvolutionPlot[{{x - 2*y, x - y}, {"noise", 1000, 1000}}, {x, -4,
4}, {y, -3, 3}, ColorFunction -> "BeachColors",
LightingAngle -> 0, LineIntegralConvolutionScale -> 3,
Frame -> False];
Manipulate[
Show[partb,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == x[t] - 2*y[t], y'[t] == -y[t] + x[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
Export["foo.gif",%]
matrixb = StreamPlot[{x - 2*y, x - y}, {x, -5, 5}, {y, -5, 5}, StreamColorFunction -> "NeonColors"]
partc = StreamPlot[{2*x + 2*y, -y - x}, {x, -4, 4}, {y, -3, 3},
StreamColorFunction -> "Rainbow"];
Manipulate[
Show[partc,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == 2*x[t] + 2*y[t], y'[t] == -y[t] - x[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
Export["foo.gif",%]
partc = LineIntegralConvolutionPlot[{{2*x + 2*y, -y - x}, {"noise", 1000,
1000}}, {x, -4, 4}, {y, -3, 3}, ColorFunction -> "BeachColors",
LightingAngle -> 0, LineIntegralConvolutionScale -> 3,
Frame -> False];
Manipulate[
Show[partc,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == 2*x[t] + 2*y[t], y'[t] == -y[t] - x[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
matrixc =
StreamPlot[{2*x + 2*y, -x - y}, {x, -5, 5}, {y, -5, 5},
StreamColorFunction -> "PlumColors"]
partd = StreamPlot[{5*x - 6*y, 3*x - 4*y}, {x, -4, 4}, {y, -3, 3},
StreamColorFunction -> "Rainbow"];
Manipulate[
Show[partd,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == 5*x[t] - 6*y[t], y'[t] == 3*x[t] - 4*y[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
partd = LineIntegralConvolutionPlot[{{5*x - 6*y, 3*x - 4*y}, {"noise", 1000,
1000}}, {x, -4, 4}, {y, -3, 3}, ColorFunction -> "BeachColors",
LightingAngle -> 0, LineIntegralConvolutionScale -> 3,
Frame -> False];
Manipulate[
Show[partd,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == 5*x[t] - 6*y[t], y'[t] == 3*x[t] - 4*y[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
matrixd =
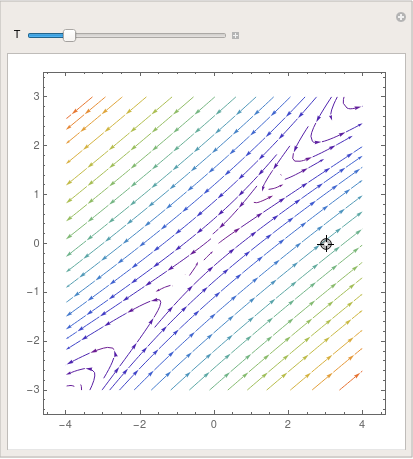
StreamPlot[{5*x - 6*y, 3*x - 4*y}, {x, -5, 5}, {y, -5, 5},
StreamColorFunction -> "StarryNightColors"]
parte = StreamPlot[{-4*x - y, 2*y + 10*x}, {x, -4, 4}, {y, -3, 3},
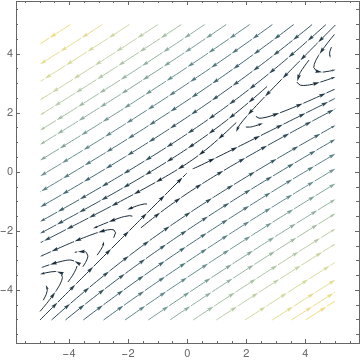
StreamColorFunction -> "Rainbow"];
Manipulate[
Show[parte,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == -4*x[t] - y[t], y'[t] == 2*y[t] + 10*x[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
parte = LineIntegralConvolutionPlot[{{-4*x - 1*y, 10*x + 2*y}, {"noise", 1000,
1000}}, {x, -4, 4}, {y, -3, 3}, ColorFunction -> "BeachColors",
LightingAngle -> 0, LineIntegralConvolutionScale -> 3,
Frame -> False];
Manipulate[
Show[parte,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == -4*x[t] - 1*y[t], y'[t] == 10*x[t] + 2*y[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]

matrixe = StreamPlot[{-4*x - y, 10*x + 2*y}, {x, -5, 5}, {y, -5, 5}, StreamColorFunction -> "Rainbow"]

There is another way to visualize solutions to vector differential e quation---use VectorPlot :

A={{1,-2},{3,5}};
Show[VectorPlot[A.{x, y}, {x, -3, 3}, {y, -3, 3}], Frame -> True,
BaseStyle -> {FontFamily -> "Times", FontSize -> 14}]

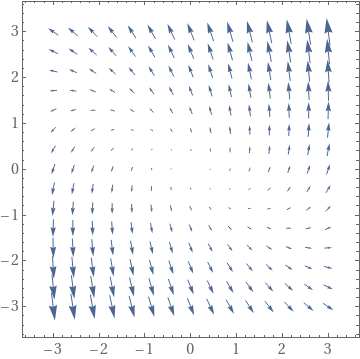
If one wants to see equal size arrows, type:

Show[VectorPlot[
A.{x, y}/(10^-8 + Norm[A.{x, y}]), {x, -3, 3}, {y, -3, 3}],
Frame -> True, BaseStyle -> {FontFamily -> "Times", FontSize -> 14}]
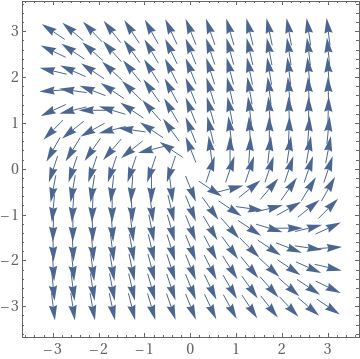
If you have a list of square matrices, and you want to determine stability of the origin for each matrix, it makes sense to organize it is a loop. For example,
A1 = {{2, 4}, {7, 5}};
A2 = {{-1, 2}, {-5, 5}};
A3 = {{1, -6}, {6, 1}};
A4 = {{-1, -2}, {1, 1}};
A5 = {{-1, -4}, {2, -5}};
A6 = {{1, -4}, {1, 5}};
A7 = {{2, -4}, {3, -5}};
Alist = {A1, A2, A3, A4, A5, A6, A7};    (*List of the different matrices*)

(*The below loop evaluates the relative signs of the eigenvalues, and \ then determines what type of critical points and stability it has. *)

Do[Print[ i, " " ];
If[(Eigenvalues[Alist[[i]]][[1]] > 0 && Eigenvalues[Alist[[i]]][[2]] > 0) && (Eigenvalues[Alist[[i]]][[ 2]] != Eigenvalues[Alist[[i]]][[1]]), Print["a) Nodal Source"]; Print["b) Unstable"]];
If[(Eigenvalues[Alist[[i]]][[1]] < 0 && Eigenvalues[Alist[[i]]][[2]] < 0) && (Eigenvalues[Alist[[i]]][[ 2]] !=E igenvalues[Alist[[i]]][[1]]), Print[ "a) Nodal Sink"]; Print[ "b) Asymptotically stable"]];
If[(Eigenvalues[Alist[[i]]][[1]] > 0 && Eigenvalues[Alist[[i]]][[2]] < 0) || (Eigenvalues[Alist[[i]]][[1]] < 0 && Eigenvalues[Alist[[i]]][[2]]> 0), Print["a) Saddle Point"]; Print["b) Unstable"]];
If[(Eigenvalues[Alist[[i]]][[1]] > 0 && Eigenvalues[Alist[[i]]][[2]] == Eigenvalues[Alist[[i]]][[1]]) && (Eigenvectors[Alist[[i]]][[ 1]] == Eigenvectors[Alist[[i]]][[2]]), Print["a) Proper Node/Star Point"]; Print["b) Unstable"]];
If[(Eigenvalues[Alist[[i]]][[1]] < 0 && Eigenvalues[Alist[[i]]][[2]]==E igenvalues[Alist[[i]]][[1]]) && (Eigenvectors[Alist[[i]]][[ 1]]==E igenvectors[Alist[[i]]][[2]]), Print[ "a) Proper Node/Star Point"]; Print[ "b) Asymptotically Stable"]];
If[(Eigenvalues[Alist[[i]]][[1]] > 0 && Eigenvalues[Alist[[i]]][[2]] == Eigenvalues[Alist[[i]]][[1]]) && (Eigenvectors[Alist[[i]]][[ 1]] != Eigenvectors[Alist[[i]]][[2]]), Print["a) Improper/Degenerate Node"]; Print["b) Unstable"]];
If[(Eigenvalues[Alist[[i]]][[1]] < 0 && Eigenvalues[Alist[[i]]][[2]]==E igenvalues[Alist[[i]]][[1]]) && (Eigenvectors[Alist[[i]]][[ 1]] !=E igenvectors[Alist[[i]]][[2]]), Print[ "a) Improper/Degenerate Node"]; Print[ "b) Asymptotically Stable"]];
If[Re[Eigenvalues[Alist[[i]]][[1]]] > 0 && Im[Eigenvalues[Alist[[i]]][[1]]] != 0, Print["a) Spiral Point"]; Print["b) Unstable"]];
If[Re[Eigenvalues[Alist[[i]]][[1]]] < 0 && Im[Eigenvalues[Alist[[i]]][[1]]] !=0 , Print[ "a) Spiral Point"]; Print[ "b) Asymptotically Zero"]];
If[Re[Eigenvalues[Alist[[i]]][[1]]] == 0 && Im[Eigenvalues[Alist[[i]]][[1]]] != 0, Print["a) Center"]; Print["b) Stable"]];
Print["c)"]; StreamPlot[{Alist[[i]][[1, 1]]*x + Alist[[i]][[1, 2]]*y, Alist[[i]][[2, 1]]*x + Alist[[i]][[2, 2]]*y}, {x, -3, 3}, {y, -3, 3}, StreamSyle->Fine] // Print, {i, 1, Legnth[Alist]}];

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions