Preface

This section gives an introduction to two dimensional (also called planar) systems of ordinary differential equations.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part III of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

The EquationTrekker package is a great package for plotting and exploring phase portraits

Planar equations

A tangent vector at each given point can be calculated directly from the given matrix-vector equation \( \dot{\bf x} = {\bf A}\,{\bf Ax} , \) using the position vector x = (x1, x2).

In first part of the course, we discussed the direction field for first order differential equations. The construction of a direction field is equally useful in the study of autonomous systems (when slope vector does not depend on time explicitly) of two first-order equations. It provides an overall view of where the solution curves go, and the arrows show which way the system moves as time increases.

A phase portrait of a planar system is a representative set of its solutions, plotted as parametric curves (with t as the parameter) on the Cartesian plane tracing the path of each particular solution (x, y) = (x1(t), x2(t)), −∞ < t < ∞. Similar to a direction field, a phase portrait is a graphical tool to visualize how the solutions of a given system of differential equations would behave in the long run. Just like a direction field, a phase portrait can be a tool to predict the behaviors of a system’s solutions. To do so, we draw a grid on the phase plane. Then, at each grid point x = (α, β), we can calculate the solution trajectory’s instantaneous direction of motion at that point by using the given system of equations to compute the tangent / velocity vector, x′ In this context, the Cartesian plane where the phase portrait resides is called the phase plane. The parametric curves traced by the solutions are sometimes also called their trajectories.

Mathematica utilizes several dedicated commands for plotting phase portraits: VectorPlot and ListVectorPlot3D, VectorDensityPlot, SliceVectorPlot3D, and StreamPlot, StreamDensityPlot, ListStreamPlot, LineIntegralConvolutionPlot; they may include ParametricPlot, DensityPlot for plotting such direction fields.

We consider systems of first order ordinary differential equations in normal form on the plane
\begin{equation} \label{EqPlanar.1} \begin{cases} \dot{x} = f (x , y) , \\ \dot{y} = g (x , y) , \end{cases} \end{equation}
where we use notation x and y for dependent variables. As usual, the overdot denotes the derivative with respect to time variable t. Of course, the above system can be written in compact vector form
\begin{equation} \label{EqPlanar.2} \frac{{\text d} {\bf x}}{{\text d}t} = {\bf f}({\bf x} ) , \end{equation}
where
\[ {\bf x} (t) = \begin{bmatrix} x (t) \\ y (t) \end{bmatrix} , \qquad {\bf f} (x , y) = \begin{bmatrix} f (x , y) \\ g (x , y) \end{bmatrix} \]
are 2-column vectors. In engineering and physics, it is a custom to denote a derivative with respect to time variable t by dot: \( \dot{\bf x} = {\text d}{\bf x} / {\text d} t. \)

If an initial position of the vector \( {\bf x} (t) \) is known, we get an initial value problem:

\[ \frac{{\text d} {\bf x}}{{\text d}t} = {\bf f}({\bf x} ) , \qquad {\bf x} (t_0 ) = {\bf x}_0 , \]
where \( {\bf x}_0 \) is a given column vector.

It is convenient to use Manipulate command to analyze dependence of solutions on some input parameters. First, we demonstrate dependence of solution of the damped pendulum equation with periodic input \( x'' + 0.1\, x' + \sin (x) = \cos t, \quad x(0) =a, \ x' (0) =0.1 \) on the input initial position.

     
Manipulate[
sol = NDSolve[{x''[t] + 0.1*x'[t] + Sin[x[t]] == Cos[t],
x[0] == xInit, x'[0] == 0.1}, {x}, {t, 0, 50}];
ParametricPlot[Evaluate[{x[t], x'[t]} /. sol, {t, 0, 20}]], {xInit, 0, 1}]
Export["pendulum4.png", %]
       Plot of solution to driven pendulum equation.            Mathematica code

A point \( {\bf a} = (a,b) \) is said to be a critical point of the planar autonomous system \eqref{EqPlanar.1} if
\[ f(a,b) =0 , \qquad g(a,b) = 0. \]
A critical point is also called an equilibrium point, a stationary point, or a rest point.
Intuitively, the equilibrium point corresponds to a state not moving away from the prescribed point, since the zero vector is attached to the equilibrium, causing the path to remain there indefinitely as time moves forward.
Let (x(t), y(t)) be a solution of a two-dimensional (planar) autonomous system \eqref{EqPlanar.1}. The trace of (x(t), y(t)) as t varies is a curve in the plane. This curve is called trajectory or orbit.
Note that two different solutions may represent the same trajectory. The trajectories do not cross. The trajectories fill the domain Ω, called the phase space, since through every point a trajectory passes. This is a consequence of existence and uniqueness theorem. Note that trajectories consisting of single point correspond to critical points.

A critical point for the system \eqref{EqPlanar.1} is called node if every orbit with arrive or depart it in a definite directory. A node is said to be a proper node if every half-line through it is a tangent to some trajectory.

For autonomous systems with two dimensional phase space, three types of trajectories are possible. A trajectory consisting of single point (corresponding to equilibrium solutions), and if trajectory has more than one point, then it could be a closed curve (corresponding to periodic solutions), or a curve without self-intersection. For autonomous systems in three or more dimensions, there could be other kinds of trajectories, including chaotic orbits (see next chapter).

There are several definitions of stability of critical points for systems of first order differential equations. Historically, the first rigorous definition of stability using ε-δ-notation was proposed in 1892 by the Russian mathematician A.M. Lyapunov (1857--1918).

Let \( {\bf a} = (a,b) \) be a critical point of the autonomous system of equations \eqref{EqPlanar.1}. The critical point a is called
  1. Stable (in the sense of Lyapunov) when, given arbitrary ε > 0, there exists a δ = δ(ε) > 0 so small that if
    \begin{equation} \label{EqStable.1a} \left\vert x(0) - a \right\vert < \delta , \qquad \left\vert y(0) - b \right\vert < \delta , \end{equation}
    then
    \begin{equation} \label{EqStable.2a} \left\vert x(t) - a \right\vert < \varepsilon , \qquad \left\vert y(t) - b \right\vert < \varepsilon , \end{equation}
    for all t > 0 and all orbits x = x(t), y = y(t) of the system \eqref{EqPlanar.1}.
  2. Asymptotically stable if it is Lyapunov stable and there exists δ > 0 such that relations \eqref{EqStable.1a} imply
    \begin{equation} \label{EqStable.3a} \lim_{t\to\infty} \left\vert x(t) - a \right\vert =0 , \qquad \lim_{t\to\infty} \left\vert y(t) - b \right\vert =0 , \end{equation}
    for all trajectories of x = x(t), y = y(t) of the system \eqref{EqPlanar.1}.
  3. Uniformly stable if, for each ε > 0 there is a δ = δ(ε) > 0 independent of the initial t0 such that
    \[ |x\left( t_0 \right) | < \delta , \quad |y\left( t_0 \right) | < \delta , \quad \Longrightarrow \quad |x(t) < \varepsilon , \ |y(t) < \varepsilon , \qquad \forall t \ge t_0 \ge 0, \]
    is satisfied, for all t0 ≥ 0.
  4. Unstable when it is not stable.

 

Critical Points of Planar Autonomous Systems

Suppose that Eq.(1) has an equilibrium point P(x*, y*) that is assumed to be isolated. And suppose further that we want to characterize the nature of the behavior of the system in the neighborhood of point P. A tempting way to proceed would be to expand functions f(x, y) and g(x, y) into Taylor series about the critical point P(x0, y0) and truncate theseries at the linear terms. The motivation for such a move is that near the equilibrium point, the quadratic and higher order terms are much smaller than the linear terms, and so they can be neglected. A convenient way to do this is to define two new coordinates ξ and η such that
\[ \xi = x- x^{\ast} , \qquad \eta = y - y^{\ast} . \]
Then we obtain
\[ \frac{{\text d}x}{{\text d}t} = \frac{{\text d}\left( x - x^{\ast} \right)}{{\text d}t} = \frac{{\text d}\xi}{{\text d}t} = \frac{\partial f}{\partial x} \,\xi + \frac{\partial f}{\partial y} \,\eta + \cdots , \qquad \frac{{\text d}y}{{\text d}t} = \frac{{\text d}\left( y - y^{\ast} \right)}{{\text d}t} = \frac{{\text d}\eta}{{\text d}t} = \frac{\partial g}{\partial x} \,\xi + \frac{\partial g}{\partial y} \,\eta + \cdots , \]
where the partial derivatives are evaluated at point P and where we have used the fact that f and g vanish at P since it is an equilibrium point. We can rewrite these expressions in concise way
\[ \frac{{\text d}}{{\text d}t} \begin{bmatrix} x(t) \\ y(t) \end{bmatrix} = \dot{\bf x} (t) = {\bf J}({\bf x}^{\ast})\,{\bf x} + \cdots = \left. \begin{bmatrix} f_x & f_y \\ g_x & g_y \end{bmatrix}\right\vert_{x=x^{\ast}, y=y^{\ast}} \begin{bmatrix} x(t) \\ y(t) \end{bmatrix} + \cdots , \]
where constant matrix J(x*) is referred to as the Jacobian matrix for Eq.\eqref{EqPlanar.1}. Now if we were satisfied with the linear approximation, we could apply the classification system described in the previous section, and we could classify a given critical point.

This sounds like a good idea, but there is a problem with it: How can we be assured that the nonlinear terms that we have truncated do not play a significant role in determining the local behavior? The answer to this question is provided by famous Grobman--Hartman theorem., discussed in section.

As an example of the sort of thing that can go wrong, consider a standard harmonic oscillator and its nonlinear perturbation:

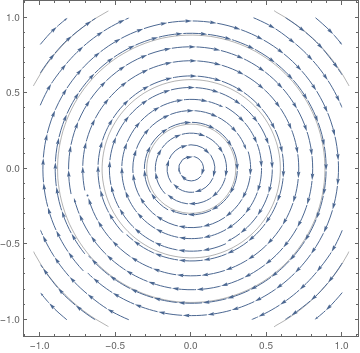
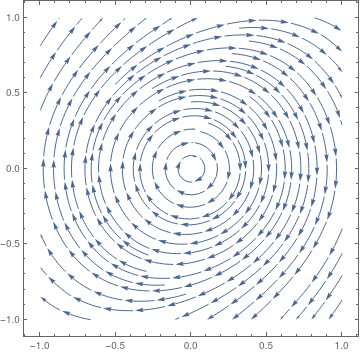
\[ \ddot{x} + x = 0 \qquad \mbox{and} \qquad \ddot{x} - \varepsilon \dot{x}^3 + x = 0 . \]
The origin (0,0) is a center for the harmonic oscilaltor because the corresponding matrix \( \begin{bmatrix} \phantom{-}0&1 \\ -1&0 \end{bmatrix} \) has two complex comjugate eigenvalues ±j. On the other hand, the perturbed system has the same Jacobian matrix, but it has unbounded solutions. Hence, its linearization does not provide corret information about behavior of solutions in a neighbohood of the origin, the equilibrium point.

     
Linear oscilaltor (stable).       Nonlinear oscillator (unstable).

StreamPlot[{y, -x}, {x, -1, 1}, {y, -1, 1}, Mesh -> 4]
StreamPlot[{y, 0.5*y^3 - x}, {x, -1, 1}, {y, -1, 1}, StreamScale -> {{0.1, 0.1}, Automatic}]

In order to use the linear equations for characterization of an equilibrium point of nonlinear system, we need sufficient conditions that guarantee the use of linearization. Since a linear system is completely characterized by its eigenvalues, we need sufficient conditions for a relation between the Jacobian and the corresponding nonlinear system.

An equilibrium point is said to be hyperbolic if all the eigenvalues of its linearized system of equations has non-zero real part.
Theorem 1 (Lyapunov): 1. An equilibrium point in a nonlinear system is asymptotically Lyapunov stable if all the eigenvalues of the corresponding Jacobian have negative real parts.
2. An equilibrium point in a nonlinear system is Lyapunov unstable if there exists at least one eigenvalue of the corresponding Jacobian that has a positive real part.

Thus, Lyapunov’s theorems state that if the equilibrium is hyperbolic, then the linearized system of equations correctly predict the Lyapunov stability in the nonlinear system. (Note that in the second of Lyapunov’s theorems, it is not necessary for the equilibrium to be hyperbolic since the presence of an eigenvalue with positive real part implies instability even if it is accompanied by other eigenvalues with zero real part.) If an equilibrium point is hyperbolic, then we saw that the linear system of equations correctlyrepresent the nonlinear system locally, as far as Lyapunov stability goes. For a hyperbolic equilibrium point, the topology of the linearized system is the same as the topology of the nonlinear system in some neighborhood of the equilibrium point. Specifically, for a hyperbolic equilibrium point P, there is a continuous 1:1 invertible transformation (a homeomorphism) defined on some neighborhood of P that maps the motions of the nonlinear system to the motions of the linearized system. This is called the Grobman--Hartman theorem

To clasify isolated equilibria, it is convenient to employ polar coordinates cenetred at the critical point: r = ρ(t), θ = ω(t). Recall that there are four types of critical points: A critical point of the nonlinear system is called center if there exists a sequence of periodic orbits {Cn} such that each of these contains all later trajectories and the origin in the interior such that
\[ C_n \to \mbox{ origin} \qquad \mbox{as} \quad n \to \infty \]
Example:
\[ \dot{x} = -y -x \sqrt{x^2 + y^2}, \qquad \dot{x} = x -y \sqrt{x^2 + y^2} \]
The polar equations corresponding the given nonlinear system of equations are
\[ \dot{r} = - r^2, \qquad \dot{x\theta} = 1 \]
The solution of this system passing through the point (r0, θ0) at t0 when r0 \ne 0 is
\[ r = \rho (t) = \frac{1}{t+ 1/r_0} , \qquad \theta = \omega (t) - t+ \theta_0 . \]
Therefore,
\[ r = \rho (t) \to 0 , \qquad \mbox{and} \qquad \theta \to \infty \qquad\mbox{as} \quad t \to +\infty . \]
The origin is a spiral although it is a center for its linear approximation.
eigenvalues linear system nonlinear system
real both positive equal proper or improper node unstable similar to node or spiral point unstable
different node unstable same
both negative equal proper or improper node as. stable similar to node or spiral point as. stable
different node as. stable same
positive and negative saddle point unstable same
complex
not real		 real part positive. spiral point unstable same
real part negative spiral point as. stable same
real part zero center stable similar to center or spiral point ?

``same'' means that type and stability for the nonlinear problem are the same as for the corresponding linear problem. If we look at at smaller and smaller neighborhoods of the critical point, the phase portrait looks more and more like the phase portrait of the corresponding linear system.

``?'' means that this cannot be determined on basis of the corresponding linear problem.

Note that the table only considers the case of nonzero eigenvalues. In this case we always have an isolated critical point.

Some Examples of Planar Systems

Example 1: The Zhukovskii problem or phugoid model, which assumesthat the wing travels with constant angle-of-attack, is a two-dimensional ordinary differentialequation for flight from which phugoid oscillations, which couple forward velocity with pitchangle, arise. Imagine a glider operating in a vertical plane. Let v be the speed of glider and u be the angle flight path makes with the horizontal axes. In the absence of drag (friction), the dimensionless equations of motion are:
\[ \frac{{\text d}v}{{\text d}t} = -\sin u - \varepsilon v^2 . \qquad v\,\frac{{\text d}u}{{\text d}t} = v^2 - \cos u , \qquad -\pi < u < \pi , \quad v> 0 . \]
When drag force is neglected (ε=0), critical points are obtained upon solving the system of equations
\[ \sin u =0, \qquad \frac{v^2 - \cos u}{v} = 0. \]
Since u = nπ,     n = 0, ±π, ±2π, …, cosing function at these points oscillates. Therefore, inside our domain, we have the only two equilibrium points: (0, ±1).

We plot phase portrates for two cases, when grad force is taking into account and when it is neglected.

vp = VectorPlot[{-Sin[u], (v^2 - Cos[u])/v}, {u, -Pi, Pi}, {v, -0.5, 1.5}, MaxRecursion -> 5];
p = StreamPlot[{-Sin[u], (v^2 - Cos[u])/v}, {u, -Pi, Pi}, {v, -0.5, 1.5}, MaxRecursion -> 5];
Show[sp, vp] sp2 = StreamPlot[{-Sin[u] - 0.5*v^2, (v^2 - Cos[u])/v}, {u, -Pi, Pi}, {v, -0.5, 1.7}, MaxRecursion -> 5];
vp2 = VectorPlot[{-Sin[u] - 0.5*v^2, (v^2 - Cos[u])/v}, {u, -Pi, Pi}, {v, -0.5, 1.5}, MaxRecursion -> 5];
Show[sp2, vp2]
     
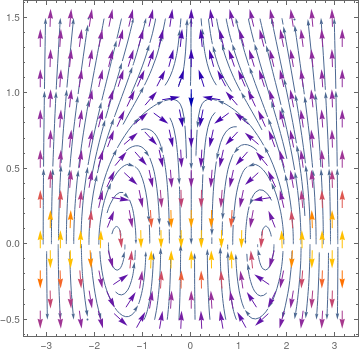
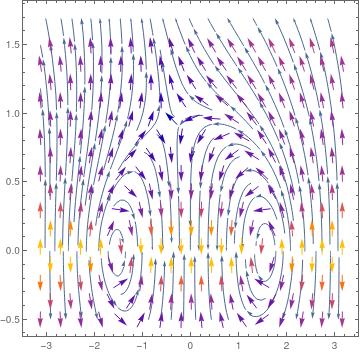
Phase portrait without drag force.       Phase portrait with drag force.
   ■
Example: Consider the dynamic system written in polar coordinates
\[ \dot{r} = \frac{r}{1+r}, \qquad \dot{\theta} = \frac{1}{1+r} \]

Consider the following non-linear system of ordinary differential equations

\[ \dot{x} = x - x^2 -xy , \qquad \dot{y} = 3y- xy - 2y^2 . \]
xdot1[x_, y_] := x - x^2 - x*y;
ydot1[x_, y_] := 3 y - x*y - 2 y^2;
a = Solve[{xdot1[x, y] == 0, ydot1[x, y] == 0}, {x, y}, Reals]
b = Reap[Do[Sow[{x, y} /. i], {i, a}]][[2, 1]]
Reap[Do[Sow[Eigenvalues[mat1[x, y] /. a[[n]]]], {n, Length[a]}]][[2, 1]]
mat1[x_, y_] = {{D[xdot1[x, y], x],
D[xdot1[x, y], y]}, {D[ydot1[x, y], x], D[ydot1[x, y], y]}}
Out[3]= {{x -> -1, y -> 2}, {x -> 0, y -> 0}, {x -> 0, y -> 3/2}, {x -> 1, y -> 0}}
Out[4]= {{-1, 2}, {0, 0}, {0, 3/2}, {1, 0}}
Out[5]=
{Eigenvalues[mat1[-1, 2]], Eigenvalues[mat1[0, 0]],
Eigenvalues[mat1[0, 3/2]], Eigenvalues[mat1[1, 0]]}
Out[6]= {{1 - 2 x - y, -x}, {-y, 3 - x - 4 y}}
c = mat1[b[[1, 1]], b[[1, 2]]]
Eigenvalues[c]
d = mat1[b[[2, 1]], b[[2, 2]]]
Eigenvalues[d]
Out[7]= {{1, 1}, {-2, -4}}
Out[8]= {1/2 (-3 - Sqrt[17]), 1/2 (-3 + Sqrt[17])}
Out[9]= {{1, 0}, {0, 3}}
Out[10]= {3, 1}
e = mat1[b[[3, 1]], b[[3, 2]]]
Eigenvalues[e]
f = mat1[b[[4, 1]], b[[4, 2]]]
Eigenvalues[f]
Out[11]= {{-(1/2), 0}, {-(3/2), -3}}
Out[12]= {-3, -(1/2)}
Out[13]= {{-1, -1}, {0, 2}}
Out[14]= {2, -1}
StreamPlot[{xdot1[x, y], ydot1[x, y]}, {x, -5, 5}, {y, -5, 5},
StreamScale -> Large, StreamStyle -> LightOrange, VectorPoints -> 10,
VectorColorFunction -> "AvocadoColors", Epilog -> {PointSize[Large], Point[b]}]

Out[23]= {{x -> -1, y -> 2}, {x -> 0, y -> 0}, {x -> 0, y -> 3/2}, {x -> 1, y -> 0}}
Out[24]= {{-1, 2}, {0, 0}, {0, 3/2}, {1, 0}}
Out[25]= {Eigenvalues[mat1[-1, 2]], Eigenvalues[mat1[0, 0]],
Eigenvalues[mat1[0, 3/2]], Eigenvalues[mat1[1, 0]]}
Out[26]= {{1 - 2 x - y, -x}, {-y, 3 - x - 4 y}}
Out[27]= {{1, 1}, {-2, -4}}
Out[28]= {1/2 (-3 - Sqrt[17]), 1/2 (-3 + Sqrt[17])}
Out[29]= {{1, 0}, {0, 3}}
Out[30]= {3, 1}
Out[31]= {{-(1/2), 0}, {-(3/2), -3}}
Out[32]= {-3, -(1/2)}
Out[33]= {{-1, -1}, {0, 2}}
Out[34]= {2, -1}

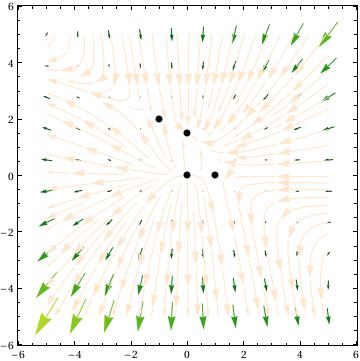
Explanation:

This command solves for all of the critical points and stores them as "a"

a = Solve[{xdot1[x, y] == 0, ydot1[x, y] == 0}, {x, y}, Reals]

This command transforms the critical points so that they are no longer in a list with x's and y's. This allows you to plot all of the critical points.

b = Reap[Do[Sow[{x, y} /. i], {i, a}]][[2, 1]]

This command creates a function of the matrix used for linearization.

mat1[x_, y_] = {{D[xdot1[x, y], x], D[xdot1[x, y], y]}, {D[ydot1[x, y], x], D[ydot1[x, y], y]}}


This command create a list of matrices, where each matrix corresponds to one of the critical points from the list in "a". Order is preserved so the first critical point will be associated with the first matrix in c.

c = mat1[x, y] /. a

This command creates a list of eigenvalues, where each set of eigenvalues corresponds to one of the critical points. Order is preserved so the first critical point will be associated with the the first set of eigenvalues.

Reap[Do[Sow[Eigenvalues[mat1[x, y] /. a[[n]]]], {n, Length[a]}]][[2, 1]]

The plot, which uses "b" to plot all of the critical point. "a" cannot be used here because it is not of the correct form for the function epilog which plots points.

StreamPlot[{xdot1[x,y], ydot1[x,y]}, {x, -5, 5}, {y, -5, 5},
StreamScale -> Large, StreamStyle -> LightOrange, VectorPoints -> 10,
VectorColorFunction -> "AvocadoColors", Epilog -> {PointSize[Large], Point[b]}]

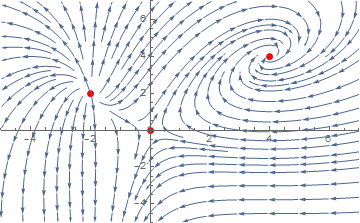
Example 2. We can plot the phase portrait manually:

sp = StreamPlot[{-x^2 - 2*x + x*y + 2*y, -x^2 + 4*x - x*y + 4*y}, {x, -5, 7}, {y, -5, 7}, PerformanceGoal -> "Quality"]
pp = ListPlot[{{0, 0}, {-2, 2}, {4, 4}}, PlotStyle -> {Thick, Red, PointSize[Large]}, PlotRange -> {{-5, 7}, {-5, 7}}]
Show[pp, sp]
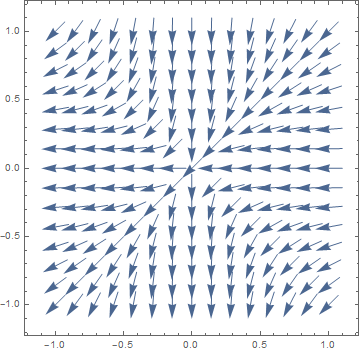
You can make use of option VectorScale. Setting None will cause all the vectors to have the same length. Or you can improvise with a custom function to make the best view of the arrows (#5 the fifth argument is vector's norm):
VectorPlot[{-(x^2/(x^2 + y^2)^(3/2)), -(y^2/(x^2 + y^2)^(3/ 2))}, {x, -1, 1},
{y, -1, 1}, VectorScale -> {Automatic, Automatic, #}] & /@ {None, Function[If[#5 > 50, None, #5^.3]]}
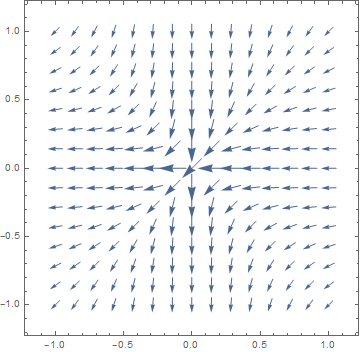In some cases, adding a potential to the vector field (in case it can be found) is a good idea:
f[x_, y_] = Integrate[ -(x*x/(x^2 + y^2)^(3/2)), x]
f2[x_, y_] = Simplify[D[f[x, y], y]]
f1[x_, y_] = Simplify[D[f[x, y], x]]
Show[ContourPlot[f[x, y], {x, -1, 1}, {y, -1, 1}, ContourStyle -> Directive[Red, Dashed],
ColorFunction -> "Rainbow", Contours -> 20],
VectorPlot[{f1[x, y], f2[x, y]}, {x, -1, 1}, {y, -1, 1},
VectorScale -> {Automatic, Automatic, Function[If[#5 > 50, None, #5^.3]]}, VectorStyle -> Black]]

 

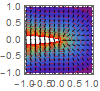
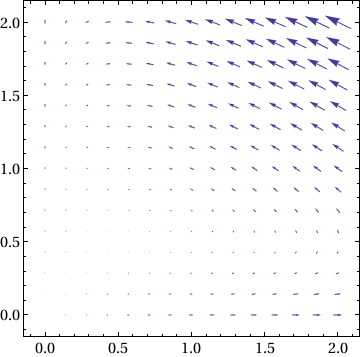
2.3.2. Autonomous Systems

f[x_, y_] = {x - 2 x y, -.5 y + x y};
Print["X' = ", MatrixForm[f[x, y]]]
Out[4]=
X' = (x-2 x y
-0.5 y+x y )
Print["x' = ", f[x, y][[1]], ", y' = ", f[x, y][[2]]]
Out[5]=
x' = x-2 x y, y' = -0.5 y+x y

Show[VectorPlot[f[x, y], {x, 0, 2}, {y, 0, 2}], Frame -> True,
BaseStyle -> {FontFamily -> "Times", FontSize -> 14}]
Show[VectorPlot[
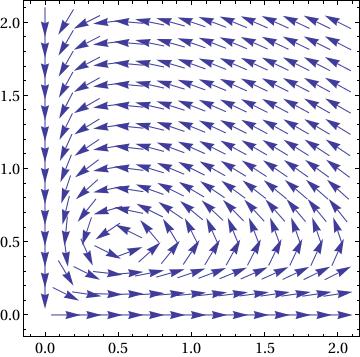
f[x, y]/(10^-8 + Norm[f[x, y]]), {x, 0, 2}, {y, 0, 2}],
Frame -> True, BaseStyle -> {FontFamily -> "Times", FontSize -> 14}]
p2 = Show[
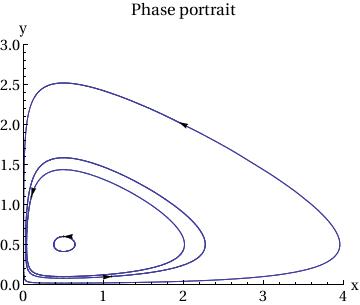
ParametricPlot[
Table[{x[t], y[t]} /. sol[[j]], {j, Length[ic]}], {t, 0, T},
PlotRange -> {{0, 4}, {0, 3}}],
Table[Graphics[{Arrowheads[.03],
Arrow[{ic[[j]], ic[[j]] + .01 f[ic[[j, 1]], ic[[j, 2]] ] }]}],
{j, Length[ic]}],
AxesLabel -> {"x", "y"},
BaseStyle -> {FontFamily -> "Times", FontSize -> 14},
PlotLabel -> "Phase portrait"
]


Plot[{x[t] /. sol[[1]], y[t] /. sol[[1]]}, {t, 0, T},
PlotStyle -> {{Thickness[0.01], RGBColor[1, 0, 0]}, {Thickness[0.01],
RGBColor[0, 1, 0]}}, AxesOrigin -> {0, 0},
AxesLabel -> {"t", "x(t),y(t)"},
BaseStyle -> {FontFamily -> "Times", FontSize -> 14},
PlotLabel -> "Time courses: Red - x(t), Green - y(t)"]

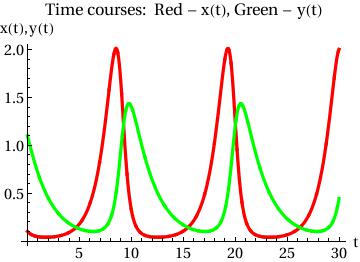
Example. Consider the system of autonomous equations

\[ \dot{x} = x^2 -3\,xy, \qquad \dot{y} = 2xy-y^2 . \]
First, we plot the direction field using StreamPLot command:
StreamPlot[{x^2 - 3*x*y, 2*x*y - y^2}, {x, -3, 3}, {y, -3, 3}]
Then we can use NDSolve function to solve the given system numerically subject to some initial conditions:
deq1 = x'[t] == x[t]^2 - 3*x[t]*y[t];
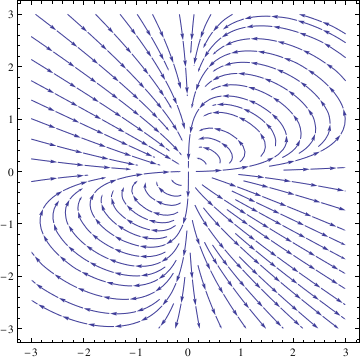
deq2 = y'[t] == 2*x[t]*y[t] - y[t]^2;
soln = NDSolve[{deq1, deq2, x[0] == 1, y[0] == 1}, {x[t], y[t]}, {t, -10, 10}];
Next, we plot the corresponding solutions curve with the command
x = soln[[1, 1, 2]]; y = soln[[1, 2, 2]]; ParametricPlot[{x, y}, {t, -10, 10}, PlotStyle -> Thick]
We can plot as many such solutions curves as we want, and then display them simultaneously. For example, the following command creates a list of solution curves corresponding to the initial conditions \( x(0) = n/10, \quad y(0) =n/10 \) for \( n=-4,-3,\ldots , 3,4. \)
curve = Table[n, {n, -4, 4}]; curvep = Table[n, {n, 0, 4}];
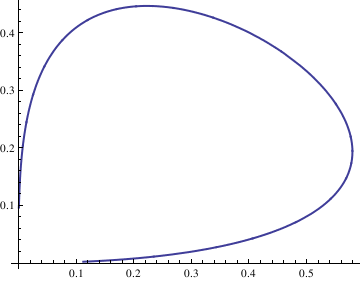
Do[Clear[x, y];
soln = NDSolve[{deq1, deq2, x[0] == n/10, y[0] == n/10}, {x[t], y[t]}, {t, -10, 10}];
x = soln[[1, 1, 2]];
y = soln[[1, 2, 2]];
curve[[n]] = ParametricPlot[{x, y}, {t, -10, 10}, PlotStyle -> Thick], {n, -4, 4}];
Show[curve[[-4]], curve[[-3]], curve[[-2]], curve[[-1]], curve[[1]], curve[[2]], curve[[3]], curve[[4]], AspectRatio -> 1]
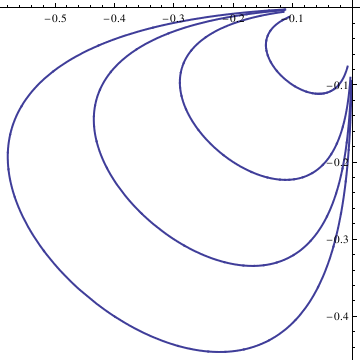
To display solutions in the first quadrant, we type:
Do[Clear[x, y];
soln = NDSolve[{deq1, deq2, x[0] == n/10, y[0] == n/10}, {x[t], y[t]}, {t, -10, 10}];
x = soln[[1, 1, 2]];
y = soln[[1, 2, 2]];
curvep[[n]] = ParametricPlot[{x, y}, {t, -10, 10}, PlotStyle -> Thick], {n, 0, 4}];
Show[curvep[[0]], curvep[[1]], curvep[[2]], curvep[[3]], curvep[[4]], AspectRatio -> 1]

 

F[x_, y_] := -y^3;
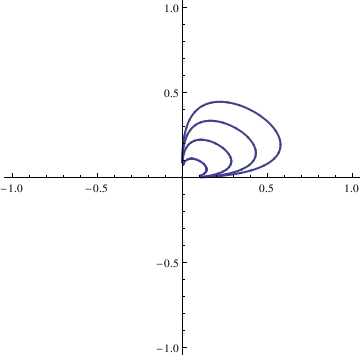
G[x_, y_] := x^3;
sol = NDSolve[{x'[t] == F[x[t], y[t]], y'[t] == G[x[t], y[t]],
x[0] == 1, y[0] == 0}, {x, y}, {t, 0, 3*Pi},
WorkingPrecision -> 20]
ParametricPlot[Evaluate[{x[t], y[t]}] /. sol, {t, 0, 3*Pi}]

X[t_] := Evaluate[x[t] /. sol]
Y[t_] := Evaluate[y[t] /. sol]
fns[t_] := {X[t], Y[t]};
len := Length[fns[t]];
Plot[Evaluate[fns[t]], {t, 0, 3*Pi}]

 

 

 

 

 

Applications

 

F[x_, y_] := -y^3;
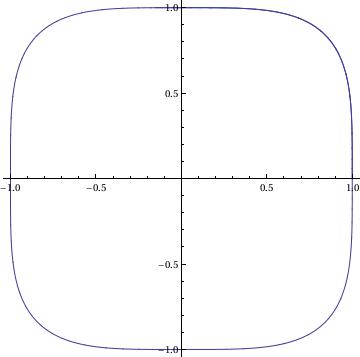
G[x_, y_] := x^3;
sol = NDSolve[{x'[t] == F[x[t], y[t]], y'[t] == G[x[t], y[t]],
x[0] == 1, y[0] == 0}, {x, y}, {t, 0, 3*Pi},
WorkingPrecision -> 20]
ParametricPlot[Evaluate[{x[t], y[t]}] /. sol, {t, 0, 3*Pi}]

Out[11]=
{{x -> InterpolatingFunction[{{0, 9.4247779607693797154}}, <>],
    y -> InterpolatingFunction[{{0, 9.4247779607693797154}}, <>]}}
X[t_] := Evaluate[x[t] /. sol]
Y[t_] := Evaluate[y[t] /. sol]
fns[t_] := {X[t], Y[t]};
len := Length[fns[t]];
Plot[Evaluate[fns[t]], {t, 0, 3*Pi}]

 

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions