MATHEMATICA

TUTORIAL

under the terms of the GNU General Public License (GPL)

for the Second Course. Part V: Even and Odd Functions

Glossary

There are two known classes of functions for which the Euler--Fourier formulas for the coefficients can be simplified: even and odd. We define them as follows

Properties involving addition and subtraction:

• The sum of two even functions is even, and any constant multiple of an even function is even.
• The sum of two odd functions is odd, and any constant multiple of an odd function is odd.
• The difference between two odd functions is odd.
• The difference between two even functions is even.
• The sum of an even and odd function is neither even nor odd, unless one of the functions is equal to zero over the given domain.

Properties involving multiplication and division:

• The product of two even functions is an even function.
• The product of two odd functions is an even function.
• The product of an even function and an odd function is an odd function.
• The quotient of two even functions is an even function.
• The quotient of two odd functions is an even function.
• The quotient of an even function and an odd function is an odd function.

Properties involving composition:

• The composition of two even functions is even.
• The composition of two odd functions is odd.
• The composition of an even function and an odd function is even.
• The composition f ○ g = f(g) of any function f with an even function g is even (but not vice versa).

Other algebraic properties:

• Any linear combination of even functions is even. The set of even functions form a vector space over the real numbers ℝ. Similarly, any linear combination of odd functions is odd, and the odd functions also form a vector space over the reals. In other words, every function f(x) can be written uniquely as the sum of an even function and an odd function:
  \[ f(x)=f_{\text{e}}(x)+f_{\text{o}}(x) , \]
  where
  \[ f_{\text{e}}(x)=\tfrac {1}{2} \left[ f(x)+f(-x) \right] , \]
  is even and
  \[ {\displaystyle f_{\text{o}}(x)={\tfrac{1}{2}}[f(x)-f(-x)]} \]
  is odd. For example, if \( f(x) = e^x , \) then its even part, f_e, is cosh(x) and its odd part, f_o, is sinh(x).

Basic calculus properties:

• The derivative of an even function is odd.
• The derivative of an odd function is even.
• The integral of an odd function from -A to +A is zero (where A is finite, and the function has no vertical asymptotes between -A and A): \( \int_{-A}^A f_{\text{o}}(x) \,{\text d}x = 0. \)
• The integral of an even function from -A to +A is twice the integral from 0 to +A (where A is finite, and the function has no vertical asymptotes between -A and A): \( \int_{-A}^A f_{\text{e}}(x) \,{\text d}x = 2 \int_0^A f_{\text{e}}(x) \,{\text d}x . \) This also holds true when A is infinite, but only if the integral converges).

Series properties:

• The Maclaurin series of an even function includes only even powers.
• The Maclaurin series of an odd function includes only odd powers.
• The Fourier series of a periodic even function includes only cosine terms.
• The Fourier series of a periodic odd function includes only sine terms.

Fourier Sine Series and Fourier Cosine Series

If a function f(x) is defined on a finite interval (𝑎, b), it can be extended periodically in three different ways:

1. Periodically with period \( T= b-a . \) This can be achieved by expanding f into regular real Fourier series:
   \begin{equation} \label{EqEven.1} f(x) \sim \frac{a_0}{2} + \sum_{n\ge 1} \left[ a_n \cos \left( \frac{2\pi nx}{T} \right) + b_n \sin \left( \frac{2\pi nx}{T} \right) \right] , \qquad a_n = \frac{2}{T} \int_T f(x) \,\cos \frac{2\pi nx}{T}\,{\text d}x , \quad b_n = \frac{2}{T} \int_T f(x) \,\sin \frac{2\pi nx}{T}\,{\text d}x ; \quad n=0,1,2,\ldots ; \end{equation}
   or complex Fourier series:
   \begin{equation} \label{EqEven.2} f(x) \sim \mbox{P.V.} \sum_{n=-\infty}^{+\infty} \hat{f}(n)\, e^{2{\bf j}\pi nx/T} , \qquad \hat{f}(n) = \frac{1}{T} \int_T f(x)\, e^{-2{\bf j}\pi nx/T} \,{\text d}x , \quad n=0, \pm 1, \pm 2, \ldots . \end{equation}
2. Periodically with period \( T= 2(b-a) = 2\ell , \) with ℓ = b−𝑎, by making the extension an even function. This can be achieved upon expanding f into Fourier cosine series:
   \begin{equation} \label{EqEven.3} f(x) \sim \frac{a_0}{2} + \sum_{n\ge 1} a_n \cos \frac{n\pi x}{\ell} , \qquad a_n = \frac{2}{\ell} \int_{0}^{\ell} f(x) \,\cos \frac{n\pi x}{\ell}\,{\text d}x ; \quad n=0,1,2,\ldots . \end{equation}
3. Periodically with period \( T= 2(b-a) = 2\ell \) by making the extension an odd function. This can be achieved upon expanding f into Fourier sine series:
   \begin{equation} \label{EqEven.4} f(x) \sim \sum_{n\ge 1} b_n \sin \frac{n\pi x}{\ell} , \qquad a_n = \frac{2}{\ell} \int_{0}^{\ell} f(x) \,\sin \frac{\pi nx}{\ell}\,{\text d}x ; \quad n=1,2,\ldots . \end{equation}

We demonstrate all these approaches in the following examples. Example 1: Fourier series for saw-tooth function

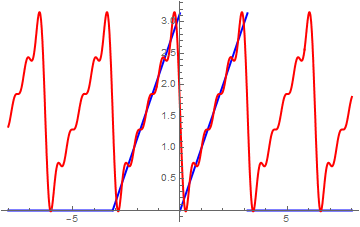
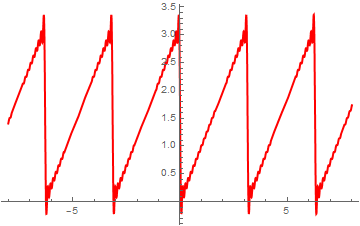
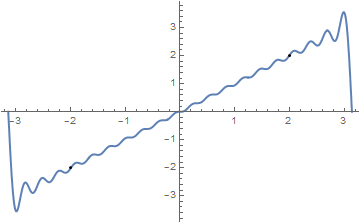
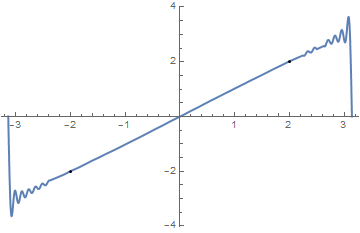
Example 1: We start with a simple function, which is of saw-tooth type: \( g(t) = t \) on the interval (0, π ) that we first extend periodically with period π and then expand it into regular Fourier series:

\[ f(t) = \begin{cases} t , & \quad \mbox{when $t\in (0, \pi )$, } \\ t + \pi , & \quad \mbox{when $t\in (-\pi , 0)$. } \end{cases} \]

a0 = Integrate[t, {t, 0, Pi}]*2/Pi
ak = Simplify[ Integrate[t*Cos[k*t], {t, 0, Pi}, Assumptions -> Element[k, Integers]]/Pi + Integrate[(t + Pi)*Cos[k*t], {t, -Pi, 0}, Assumptions -> Element[k, Integers]]/Pi ]
bk = Simplify[ Integrate[t*Sin[k*t], {t, 0, Pi}, Assumptions -> Element[k, Integers]]/Pi + Integrate[(t + Pi)*Sin[k*t], {t, -Pi, 0}, Assumptions -> Element[k, Integers]]/Pi ]
fourier[m_] := Pi/2 + Sum[ak*Cos[k*t] + bk*Sin[k*t], {k, 1, m}]

\[ f(t) = \frac{\pi}{2} - \sum_{k\ge 0} \frac{1}{k} \left[ 1+ (-1)^k \right] \sin (kt) = \frac{\pi}{2} - \sum_{n\ge 1} \frac{1}{n} \, \sin (2n\,t) . \]

There are three options to determine the Fourier series. First, we define a piecewise continuous function

f[t_] = Piecewise[{{t + Pi, -Pi < x < 0}, {t, 0 < t < Pi}}]

With this at hand, we can either evaluate Fourier coefficients directly

an = Assuming[Element[n, Integers], Integrate[f[x]*Cos[n*x], {x, -Pi, Pi}]/Pi]
bn = Assuming[Element[n, Integers], Integrate[f[x]*Sin[n*x], {x, -Pi, Pi}]/Pi]

or use standard Mathematica command (to see 10 first coefficients)

FourierTrigSeries[f[x], x, 10]

Another option is to consider the given function of the interval (0, π):

\[ f(x) = \frac{a_0}{2} + \sum_{n\ge 1} a_n \cos (2nx) + b_n \sin (2nx) , \]

where

\begin{align*} a_0 &= \frac{2}{\pi} \int_0^{\pi} t\,{\text d}t = \pi , \\ a_n &= \frac{2}{\pi} \int_0^{\pi} t\,cos (2nt)\, {\text d}t = 0, \qquad n> 0, \\ b_n &= \frac{2}{\pi} \int_0^{\pi} t\,sin (2nt)\, {\text d}t = \frac{1}{n} , \qquad n=1,2,\ldots . \end{align*}

An = 2*Integrate[t*Cos[2*n*t], {t, 0, Pi}]/Pi
Bn = 2*Integrate[t*Sin[2*n*t], {t, 0, Pi}]/Pi

Then we plot partial sums with 10 and 50 terms:

f[x_] = Piecewise[{{x, 0 < x < Pi}, {x + Pi, -Pi < x < 0}}]
Plot[{f[t], fourier[50]}, {t, -8, 8}, PlotStyle -> {{Thick, Blue}, {Thick, Red}}]

Now we extend the given function in even way on the interval \( (-\pi , \pi ) . \) This interval was chosen for simplicity to avoid application of option FourierParameters that was explained in the introductory web page.

periodicExtension[func_] := func[Abs[Mod[t, 2*Pi, -1*Pi]]]
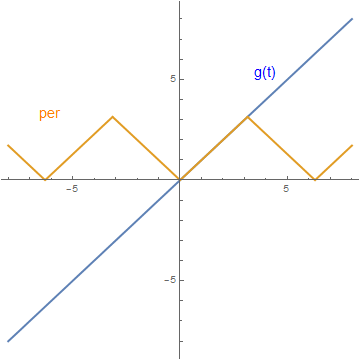
g[t_] = t
per = periodicExtension[g]
a = Plot[{g[t], per}, {t, -8, 8}, PlotStyle -> Thick, AspectRatio -> 1]
Show[a, Graphics[{Text[Style["g(t)", FontSize -> 14, Blue], {4, 5.3}], Text[Style["per", FontSize -> 14, Orange], {-6, 3.3}]}]]

Now we turn our attention to even extension of the given function:

\[ f_e (t) = \begin{cases} \phantom{-}t , & \quad \mbox{when $t\in (0, \pi )$, } \\ -t , & \quad \mbox{when $t\in (-\pi , 0)$. } \end{cases} \]

Its cosine Fourier expansion is

\[ f_e (t) = \frac{\pi}{2} +\frac{2}{\pi} \, \sum_{k\ge 0} \frac{1}{k^2} \left[ (-1)^k -1\right] \cos (kt) = \frac{\pi}{2} - \frac{4}{\pi}\,\sum_{k\ge 0} \frac{1}{(2k+1)^2} \, \cos ((2k+1)t) . \]

We plot partial cosine Fourier sums with 10 and 50 terms:

a0 = Integrate[t, {t, 0, Pi}]*2/Pi
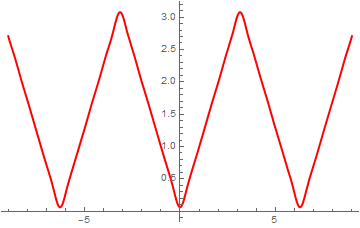
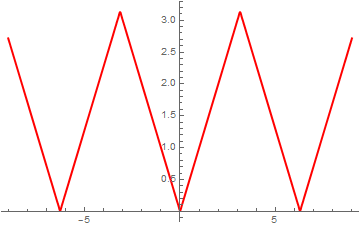
ak = Simplify[Integrate[t*Cos[k*t], {t, 0, Pi}]*2/Pi ]
even[m_] := Pi/2 + Sum[ak*Cos[k*t], {k, 1, m}]
Plot[{even[50]}, {t, -8, 8}, PlotStyle -> {Thick, Red}]

Since the function g(t) = t is an odd function, we apply the Mathematica command FourierTrigSeries[g[t], t, 5] to find its sine Fourier series approximation with 5 terms:

Out[4]= 2 Sin[t] - Sin[2 t] + 2/3 Sin[3 t] - 1/2 Sin[4 t] + 2/5 Sin[5 t]

We check the answer with manual evaluation:

bk = Integrate[t*Sin[k*t], {t, 0, Pi}]*2/Pi

Out[5]= (-2 k \[Pi] Cos[k \[Pi]] + 2 Sin[k \[Pi]])/(k^2 \[Pi])

Therefore, the odd extension of the function g(t) becomes

\[ t = -2\,\sum_{k\ge 1} \frac{1}{k} \, (-1)^k \sin (kt) , \quad t \in (-\pi, \pi ). \]

Then we plot sine Fourier approximations with 10 and 50 terms:

odd[m_] = -2*Sum[(-1)^k/k*Sin[k*t], {k, 1, m}]
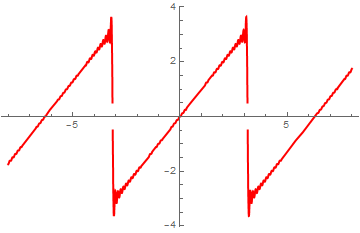
Plot[odd[10], {t, -8, 8}, PlotStyle -> {Thick, Red}]

 

FourierSinCoefficient[ expr , t, n] gives the n-th coefficient in the Fourier sine series expansion of expr.
FourierCosCoefficient[ expr , t, n] gives the n-th coefficient in the Fourier cosine series expansion of expr.
FourierCosSeries[expr, t , n] gives the n-order Fourier cosine series expansion of expr in t.
FourierSinSeries[expr, t , n] gives the n-order Fourier sine series expansion of expr in t.

 

Similarly, we get sine Fourier series (Gibbs overshoot and undershoot are given explicitly):

FourierSinSeries[x, x, 50, FourierParameters -> {1, Pi/2}];
Plot[%, {x, -1.5, 3.5}, PlotStyle -> Thick, Ticks -> {{-1, 1, 3}, {2.358, -2.358}}]

Finally, we demonstrate animation for Fourier series approximations. s[x_, m_] = Pi/2 - Sum[Sin[2*n*x]/n, {n, 1, m}]; animation = Table[Plot[s[x, m], {x, -0.1, Pi + 0.1}, PlotRange -> {0, 3.2}, PlotStyle -> Thickness[0.008], PlotLabel -> "Fourier approximation depends on " <> ToString[m] <> " terms"], {m, 0, 100, 2}]; Export["saw.gif", animation, "AnimationRepetitions" -> 200]

Example 2: Let us consider the function f(x) = x, assuming it is defined in the interval [-π , π ].

f[x_] := x
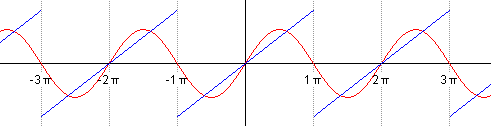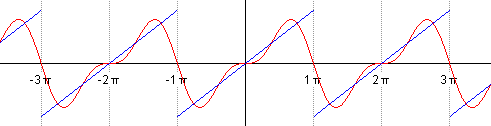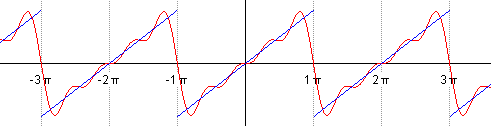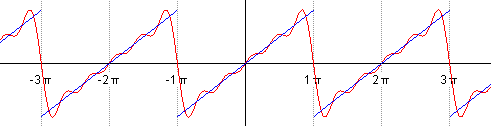
a0 = (1/Pi)* Integrate[f[x], {x, −Pi, Pi}];
an = (1/Pi)* Integrate[f[x]*Cos[n*x], {x, −Pi, Pi}, Assumptions -> Element[n, Integers]];
bn = (1/Pi)* Integrate[f[x]*Sin[n*x], {x, −Pi, Pi}, Assumptions -> Element[n, Integers]];
Print[{a0, an, bn}]

Out[5]= {0,0,(2 (-n \[Pi] Cos[n \[Pi]]+Sin[n \[Pi]]))/(n^2 \[Pi])}

Note that we used option Assumptions to tell Mathematica that n is an integer. Then we define the finite sum Fourier approximation containing m terms:

fourier[m_] := a0 /2 + Sum[an Cos[n x] + bn Sin[n x], {n, 1, m}]
Plot[fourier[10], {x, -Pi, Pi}, Epilog -> Point[{{2, 2}, {-2, -2}}], PlotStyle -> {Thick, Black}]

Now we repeat calculations with m=20 and m=50 terms:

Plot[fourier[20], {x, -Pi, Pi}, Epilog -> Point[{{2, 2}, {-2, -2}}], PlotStyle -> Thick]
Plot[fourier[50], {x, -Pi, Pi}, Epilog -> Point[{{2, 2}, {-2, -2}}], PlotStyle -> Thick]

Example 3: Since the function sin(x/2) is an odd function on the interval [-π,π], we can expand it into sine Fourier series explicitly:

\[ \sin \left( \frac{x}{2} \right) \sim \frac{2}{\pi} \sum_{n\ge 1} (-1)^{n+1} \frac{n}{n^2 -1/4} \,\sin (nx) , \qquad x\in (-\pi , \pi ). \]

We check with Mathematica whether partial sums approximate the given function:

F[x_]=2/Pi*Sum[(-1)^(n+1)*n/(n*n-1/4) * Sin[n*x] , {n,1,30}];
Plot[{Sin[x/2], F[x]}, {x,-5,5}, PlotStyle->Thick]

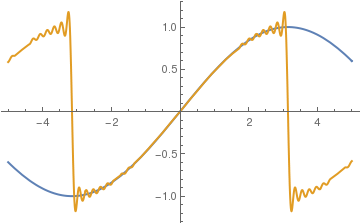
We can also expand the given function sin(x/2) into cosine Fourier series by expanding it to negative semi-axis in even way. First, we calculate Fourier coefficients:

a0=2/Pi*Integrate[Sin[x/2], {x,0,Pi}];
an= Simplify[2/Pi*Integrate[Sin[x/2]*Cos[n*x], {x,0,Pi}]];

4/\[Pi]
(4 - 8 n Sin[n \[Pi]])/(\[Pi] - 4 n^2 \[Pi])

This gives us the following cosine Fourier series:

\[ \sin \left( \frac{x}{2} \right) \sim \frac{2}{\pi} - \frac{4}{\pi} \sum_{n\ge 1} \frac{1}{4n^2 -1} \, \cos (nx) , \qquad x\in [-\pi , \pi ] . \]

F[x_]= 2/Pi - 4/Pi*Sum[1/(4*n*n-1) * Cos[n*x], {n,1,30}];
Plot[{Sin[x/2], F[x]}, {x,-5,10}, PlotStyle->Thick]

So the partial sum with 30 terms gives a very good approximation for the function sin(x/2) on the interval [0,π]. ■

Example 4: Now we use cosine and sine Fourier series for the half-wave rectifier of function f(x) = 1-x:

\[ f(x) = \begin{cases} 1-x , & \ \mbox{ if } 0 < x < 1, \\ 0, & \ \mbox{ if } 1 < x < 2. \end{cases} \]

Let us start with cosine series, which gives even periodic expansion of the given function:

f[x_] = Piecewise[{{1 - x, 0 < x < 1}, {0, 1 < x < 2}}];
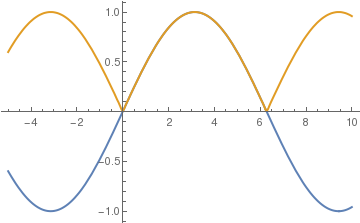
FourierCosSeries[f[x], x, 3]

out[10]= 1/(2 \[Pi]) + (4 Cos[x] Sin[1/2]^2)/\[Pi] + (
Cos[2 x] Sin[1]^2)/\[Pi] + (4 Cos[3 x] Sin[3/2]^2)/(9 \[Pi])

coscurve5Pi=FourierCosSeries[f[x], x, 5];
Plot[coscurve5Pi, {x, -1.5, 3.5}]

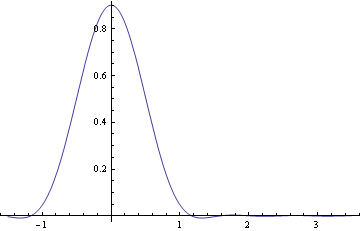
then with 50 terms:

coscurve50Pi=FourierCosSeries[f[x], x, 5];
Plot[coscurve50Pi, {x, -1.5, 3.5}]

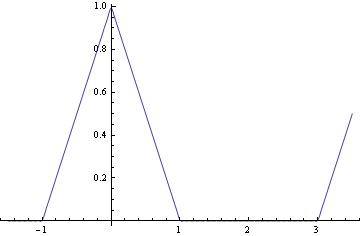
Then we repeat these calculation for cosine series on the interval of length 2:

FourierCosSeries[f[x], x, 5, FourierParameters -> {1, Pi/2}];
Plot[%, {x, -1.5, 3.5}]

We can also find sine Fourier series for this piecewise function.

f[x_] = Piecewise[{{1 - x, 0 < x < 1}, {0, 1 < x < 2}}];
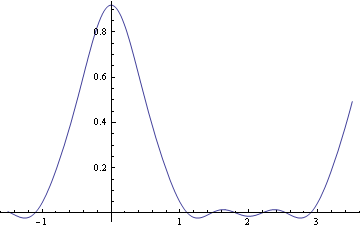
FourierSinSeries[f[x], x, 25, FourierParameters -> {1, Pi/2}];
Plot[%, {x, -1.5, 3.5}, PlotStyle->Thick, PlotRange->{-1.1,1.1}]

■

We consider two examples for derivations of trigonometric identities using Fourier series expansions.

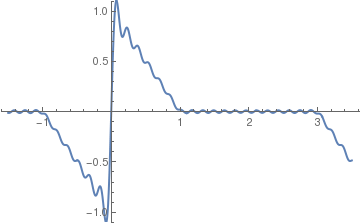
Example 5A: We are going to prove the well-known trigonometric identity:

\[ \cos^2 x = \frac{1+ \cos 2x}{2} . \]

Since the cosine function is an even periodic function with the fundamental period 2π, we expand its product with itself into cosine Fourier series

\[ \cos^2 x = \frac{a_0}{2} + \sum_{k\ge 1} a_k \cos \left( \frac{k\pi x}{L} \right) , \qquad \mbox{with } L = \pi . \]

The Euler-Fourier coefficients are determined with Mathematica:

f[x_] = (Cos[x])^2
L=Pi
a0 = 2/L*Integrate[f[x], {x, 0, L}]
ak = 2/L*Integrate[f[x]*Cos[x*k*Pi/L], {x, 0, L}]

(2 (-2 + k^2) Sin[k \[Pi]])/(k (-4 + k^2) \[Pi])

Since sin kπ = 0 for any integer k, all coefficients \( a_k = 0 \) except k = 2, which we calculate separately:

a2 = 2/L*Integrate[f[x]*Cos[x*2*Pi/L], {x, 0, L}]

1/2

Therefore, the Fourier expansion of the function cos² contains only two nonzero terms corresponding to k = 0 and k = 2. This proves the identity above.

However, we notice that cos² is actually a periodic function with period π, so we can find its cosine Fourier series with 2 L = π:

\[ \cos^2 x = \frac{a_0}{2} + \sum_{k\ge 1} a_k \cos \left( \frac{k\pi x}{L} \right) , \qquad \mbox{with } L = \pi /2. \]

Mathematica helps:

L=Pi/2
a0 = 2/L*Integrate[f[x], {x, 0, L}]
ak = 2/L*Integrate[f[x]*Cos[x*k*Pi/L], {x, 0, L}]

(4 Sin[k \[Pi]])/((4 k - 4 k^3) \[Pi])

This yields

\[ \cos^2 x = \frac{1}{2} + \sum_{k\ge 1} \frac{2 \, \sin k\pi}{k \left( k-1 \right)\left( k+1 \right) \pi} \cos \left( 2k\pi x \right) . \]

Again, the coefficient \( a_1 \) should be calculated separately because it is undefined as 0/0.

a1 = 2/L*Integrate[f[x]*Cos[x*1*Pi/L], {x, 0, L}]

1/2

So we again obtain the correct answer.

Now we consider another function that coincides with cos²x on the interval (-π,π):

\[ f_1 (x) = \begin{cases} -\cos^2 x , & \ \pi /2 \le x \le \pi , \\ \phantom{-}\cos^2 x , & \ -\pi /2 \le x \le \pi /2 , \\ -\cos^2 x , & \ -\pi \le x \le -\pi /2 . \end{cases} \]

We expand this even function defined on the interval (-π,π) into Fourier series

\[ f_1 (x) = \sum_{n\ge 0} a_n \cos \left( n\pi x \right) , \]

where \( a_0 =0 \) and

\[ a_n = \frac{2}{\pi} \int_0^{\pi /2} \cos^2 x\,\cos \left( n\, x \right) {\text d}x - \frac{2}{\pi} \int_{\pi /2}^{\pi} \cos^2 x\,\cos \left( n\, x \right) {\text d}x = - \frac{4}{\pi}\,\frac{\sin n\pi /2}{n \left( n-2 \right) \left( n+2 \right)} \]

because

an = Integrate[f[x]*Cos[n*x], {x, 0, Pi/2}] - Integrate[f[x]*Cos[n*x], {x, Pi/2, Pi}]

-((2 Sin[(n \[Pi])/2])/(-4 n + n^3)) - ( 2 Sin[(n \[Pi])/2] + (-2 + n^2) Sin[n \[Pi]])/(n (-4 + n^2))

Finally, we get

\[ f_1 (x) = - \frac{4}{\pi} \sum_{k\ge 0} \frac{2\, (-1)^k}{\left( 2k+1 \right)\left( 2k-1 \right)\left( 2k+3 \right)} \, \cos \left( 2k+1 \right) x . \]

Therefore, we have two Fourier representations for the same function cos²x on the interval (−π, π) but with respect to different sets of cosine functions. Finally, we plot cos²x along with 10-term cosine Fourier approximation to the function f₁(x).

F[x_] = - (4/Pi)* Sum[2*(-1)^k *Cos[(2*k + 1)*x]/(4*k^2 - 1)/(2*k + 3), {k, 0, 10}]
a = Plot[{F[x], (Cos[x])^2}, {x, -4, 4}, PlotStyle -> Thick]
text1 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(f\), \(1\)]\)(x)", FontSize -> 14, Black], {1.4, -0.6}]]
text2 = Graphics[ Text[Style["\!\(\*SuperscriptBox[\(cos\), \(2\)]\)(x)", FontSize -> 14, Black], {1.6, 0.6}]]
Show[a, text1, text2]

Example 5B: Now we derive the identity:

\[ \cos^3 x = \frac{\cos 3x + 3\, \cos x}{4} . \]

First, we start with cosine Fourier series on the interval (−π, π):

\[ \cos^3 x = \sum_{k\ge 1} A_k \cos \cos \left( \frac{k\pi x}{L} \right) , \qquad \mbox{with } L = \pi . \]

The Euler-Fourier coefficients are determined with Mathematica:

g[x_] = (Cos[x])^3;
L = Pi a0 = 2/L*Integrate[g[x], {x, 0, L}]
ak = 2/L*Integrate[g[x]*Cos[x*k*Pi/L], {x, 0, L}]
a2 = 2/L*Integrate[g[x]*Cos[x*2*Pi/L], {x, 0, L}]

-((2 k (-7 + k^2) Sin[k \[Pi]])/((9 - 10 k^2 + k^4) \[Pi]))

These coefficients are all zeroes except values where the denominator vanishes. So we find its roots:

Solve[9 - 10 k^2 + k^4 == 0, k]

{{k -> -3}, {k -> -1}, {k -> 1}, {k -> 3}}

So we need to recalculate coefficients corresponding to indices k = 1 and 3.

a1 = 2/L*Integrate[g[x]*Cos[x*1*Pi/L], {x, 0, L}]
a3 = 2/L*Integrate[g[x]*Cos[x*3*Pi/L], {x, 0, L}]

3/4
1/4

Therefore, we get

\[ \cos^3 x = \frac{3}{4}\,\cos x + \frac{3}{4}\, \cos 3x . \]

Now we repeat calculations for the cosine Fourier series on the interval (0,π/2).

\[ \cos^3 x = \frac{A_0}{2} + \sum_{k\ge 1} A_k \cos \cos \left( 2k\pi x \right) , \qquad A_k = \frac{4}{\pi} \int_0^{\pi /2} \cos^3 x\, \cos \left( 2k\pi x \right) {\text d}x . \]

L = Pi/2
a0 = 2/L*Integrate[g[x], {x, 0, L}]
ak = 2/L*Integrate[g[x]*Cos[x*k*2], {x, 0, L}]

(24 Cos[k \[Pi]])/((9 - 40 k^2 + 16 k^4) \[Pi])

The denominator vanishes for noninteger values:

Solve[9 - 40 k^2 + 16 k^4 == 0, k]

{{k -> -(3/2)}, {k -> -(1/2)}, {k -> 1/2}, {k -> 3/2}}

We conclude that

\[ \cos^3 x = \frac{4}{3\pi} + \frac{24}{\pi} \sum_{k\ge 1} \frac{(-1)^k}{9-40 k^2 + 16 k^4} \,\cos \left( 2k\pi x \right) . \]

So we obtained two cosine Fourier series for cos³x on the interval (-π/2,π/2).    ■

Example 6: We consider an integrable function that does not satisfy the Dirichlet conditions and for which we don't have sufficient conditions that guarantee pointwise convergence of the corresponding Fourier series (which is actually the Fourier sine series because the function is odd).

\[ f(x) = \sin \left( \frac{1}{x} \right) , \qquad -\ell < x < \ell . \tag{6.1} \]

This function belongs to 𝔏²(−ℓ, ℓ) for any positive ℓ. For simplicity, we set ;ℓ = 1 and get

f[x_] = Sin[1/x] N[Integrate[f[x]^2, {x,-1,1}]]

1.3469135365315457

\[ \int_{-1}^1 f^2 (x)\,{\text d}x =\int_{-1}^1 \sin^2 \left( \frac{1}{x} \right) \,{\text d}x \approx 1.3469135365315457 . \]

We formally expand this function into Fourier sine series

\[ \sin \left( \frac{1}{x} \right) = \sum_{n\ge 1} b_n \sin \left( \pi x \right) , \tag{6.2} \]

where coefficients

\[ b_n = 2 \int_0^1 \sin \left( \frac{1}{x} \right) \sin \left( n \pi x \right) {\text d} x , \qquad n= 1 ,2 , 3, \ldots , \tag{6.3} \]

can be evaluated only numerically.

SF10[x_] = Sum[2 *NIntegrate[Sin[1/x]*Sin[n*Pi*x], {x, 0, 1}]*Sin[n*Pi*x], {n, 10}];
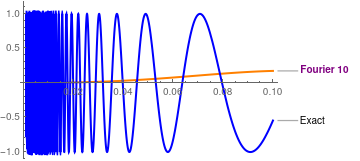
Plot[{Callout[SF10[x], "Fourier 10", LabelStyle -> Directive[Purple, Bold]], Callout[Sin[1/x], "Exact"]}, {x, 0, 1}, PlotStyle -> {{Thick, Orange}, {Thick, Blue}}]
Plot[{Callout[SF10[x], "Fourier 10", LabelStyle -> Directive[Purple, Bold]], Callout[Sin[1/x], "Exact"]}, {x, 0.001, 0.1}, PlotStyle -> {{Thick, Orange}, {Thick, Blue}}]

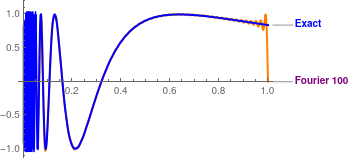
Then we repeat calculations with 100 terms:

SF100[x_] = Sum[2 *NIntegrate[Sin[1/x]*Sin[n*Pi*x], {x, 0, 1}]*Sin[n*Pi*x], {n, 100}];
Plot[{Callout[SF100[x], "Fourier 100", LabelStyle -> Directive[Purple, Bold]], Callout[Sin[1/x], "Exact", LabelStyle -> Directive[Blue, Bold]]}, {x, 0.001, 1}, PlotStyle -> {{Thick, Orange}, {Thick, Blue}}]
Plot[{Callout[SF100[x], "Fourier 100", LabelStyle -> Directive[Purple, Bold]], Callout[Sin[1/x], "Exact", LabelStyle -> Directive[Blue, Bold]]}, {x, 0.001, 0.1}, PlotStyle -> {{Thick, Orange}, {Thick, Blue}}]

We apply Cesàro summation.

CF100[x_] = Sum[(1 - n/100)*2 *NIntegrate[Sin[1/x]*Sin[n*Pi*x], {x, 0, 1}]* Sin[n*Pi*x], {n, 100}];
Plot[{Callout[CF100[x], "Cesaro 100", LabelStyle -> Directive[Red, Bold]], Callout[Sin[1/x], "Exact", LabelStyle -> Directive[Blue, Bold]]}, {x, 0.005, 1}, PlotStyle -> {{Thick, Red}, {Thick, Blue}}]
Plot[{Callout[CF100[x], "Cesaro 100", LabelStyle -> Directive[Red, Bold]], Callout[Sin[1/x], "Exact", LabelStyle -> Directive[Blue, Bold]]}, {x, 0.005, 0.1}, PlotStyle -> {{Thick, Red}, {Thick, Blue}}]

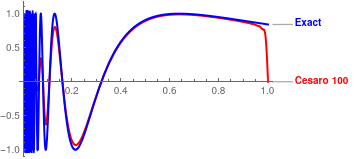
Finally, we take 1000 terms:

SF1000[x_] = Sum[2 *NIntegrate[Sin[1/x]*Sin[n*Pi*x], {x, 0, 1}]*Sin[n*Pi*x], {n, 1000}];
Plot[{Callout[SF1000[x], "Fourier 1000", LabelStyle -> Directive[Purple, Bold]], Callout[Sin[1/x], "Exact", LabelStyle -> Directive[Blue, Bold]]}, {x, 0.005, 1}, PlotStyle -> {{Thick, Orange}, {Thick, Blue}}]
Plot[{Callout[SF1000[x], "Fourier 1000", LabelStyle -> Directive[Purple, Bold]], Callout[Sin[1/x], "Exact"]}, {x, 0.005, 0.02}, PlotStyle -> {{Thick, Orange}, {Thick, Blue}}]

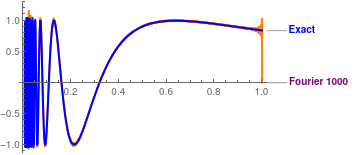
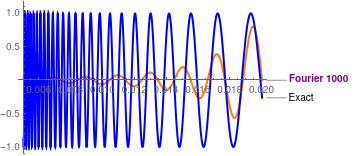
Cesàro summation gives:
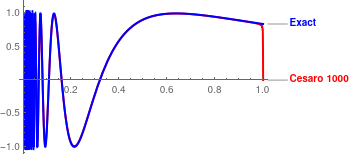
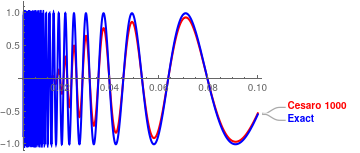
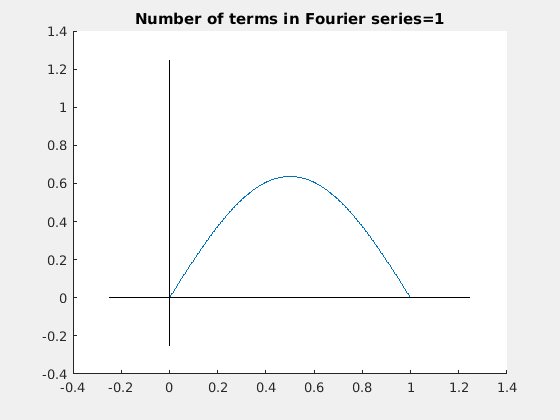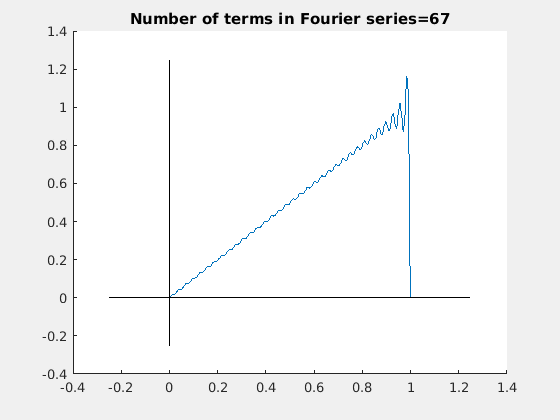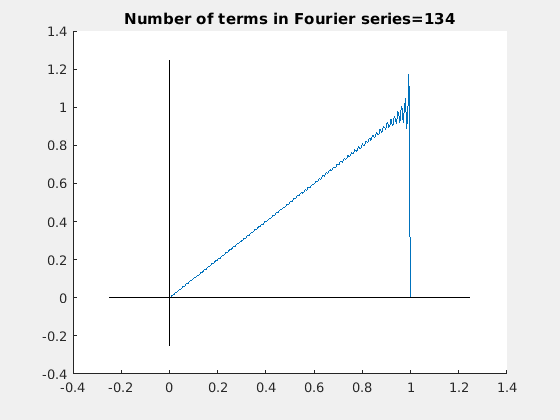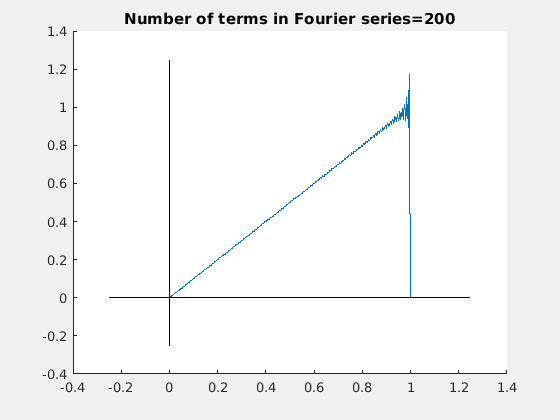
We compare which of two approximations, Fourier or Cesàro, gives a better approximation using their graphical outputs. Since human's eyes have a resolution of about 5%, it gives us only qualitative conclusion. Working with 1000-term approximations, we conclude that the Cesàro approximation is accurate enough after x > 0.1. When x → 0, Cesàro approximation tends to zero and does not match the function. On the other hand, Fourier approximation gives a reasonable accuracy forx > 0.04, but exhibits the Gibbs phenomenon at the boundary x = 1,
   ■

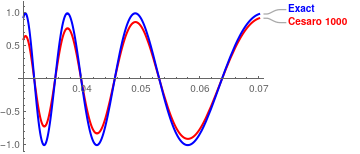
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions