Preface

Newmerical solutions of the system of algebraic equations is the topic of this section.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part IV of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

In certain cases, such as when a system of equations is large, iterative methods of solving equations such as Gauss--Seidel method are more advantageous. Elimination methods, such as Gaussian Elimination, are prone to round-off errors for a large set of equations whereas iterative methods allow the user to control round-off error. Also if the physics of the problem are well known, initial guesses needed in iterative methods can be made more judiciously for faster convergence.

Jacobi Iteration

We start with an example that clarifies the method.

Example: Consider the system of equations

\[ \begin{split} 4x-2y+z&=9, \\ 2x+8y-3z&=19, \\ x+2y -5z&=2. \end{split} \]
These equations can be written in the form
\[ \begin{split} x&= (9+2y-z)/4 , \\ y&=(19-2x+3z)/8 , \\ z&=(x+2y-2)/5. \end{split} \]
This suggests the following Jacobi itterative process
\[ \begin{split} x_{k+1}&= (9+2y_k -z_k )/4 , \\ y_{k+1}&=(19-2x_k +3z_k )/8 , \\ z_{k+1}&=(x_k +2y_k -2)/5. \end{split} \]
Starting with some initial values, say (2,1,0), we fill out the table
i  x_i  y_i  z_i 
0  2  1  0 
1  2.75  1.875  0.4 
2  3.0875  1.8375  0.9 
3  2.94375  1.94062  0.9525 
4  2.98219  1.99625   0.965 
5  3.00688  1.99133  0.994938 
6  2.99693  1.99638  0.997906 
7  2.99871  1.99998  0.997939 
8  3.00051  1.99955  0.999736 
9  2.99984  1.99977  0.999921 
10  2.99991  2.00001  0.999878 
This iterative process unambiguously indicates that the given system has the solution (3,2,1).
x[0] = 2; y[0] = 1; z[0] = 0;
Do[{x[i + 1] = N[(9 + 2*y[i] - z[i])/4], y[i + 1] = N[(19 - 2*x[i] + 3*z[i])/8], z[i + 1] = N[(x[i] + 2*y[i] - 2)/5]}, {i, 0, 10}]
Do[Print["i=", i, " x= ", x[i], " y= ", y[i], " z= ", z[i]], {i, 0, 10}]
■

This process is called Jacobi iteration and can be used to solve certain types of linear systems. it is named after the German mathematician Carl Gustav Jacob Jacobi (1804--1851), who made fundamental contributions to elliptic functions, dynamics, differential equations, and number theory. His first name is sometimes given as Karl and he was the first Jewish mathematician to be appointed professor at a German university.

Linear systems with as many as 100,000 or more variables often arise in the solutions of partial differential equations (Chapter 7). The coefficient matrices for these systems are sparse; that is, a large percentage of the entries of the coefficient matrix are zero. An iterative process provides an efficient method for solving these large systems.

Sometimes the Jacobi mathod does not work. Let us experiment with the following system of equations.

Example: Consider the system of equations

\[ \begin{split} 4x-2y+8z&=16, \\ 2x+y-5z&=3, \\ 5x+2y -z&=18. \end{split} \]
We rewrite these equations as
\[ \begin{split} x&= (16+2y-8z)/4 , \\ y&= 3-2x+5z , \\ z&= 5x +2y-18. \end{split} \]
This suggests the following Jacobi iterative process
\[ \begin{split} x_{k+1}&= (9+2y_k -z_k )/4 , \\ y_{k+1}&=(19-2x_k +3z_k )/8 , \\ z_{k+1}&=(x_k +2y_k -2)/5. \end{split} \]
Starting with some initial values, say (2,1,0), we fill out the table
i  x_i  y_i  z_i 
0  2  1  0 
1  4.5  -1  -6 
2  15.5  -36  2.5 
3  -19  -15.5  -12.5 
4  21.25  -21.5   -144. 
5  281.25  -759.5  45.25 
6  -466.25  -333.25  -130.75 
7  98.875  281.75  -3015.75 
8  6176.38  -15273.5  1039.88 
9  -9712.5  -7150.38  316.875 
10  -4204.94  21012.4  62881.3 
So this iterative process cannot converge to (3,2,1), true solution. ■

The last example shows that we need some criterion to determine whether the Jacobi iteration will converge. Hence, we make the following definition.

A square matrix A of dimensions \( n \times n \) is said to be strictly diagonally dominated provided that

\[ | a_{k,k} | > \sum_{j=1, j\ne k}^n |a_{k,j}| \qquad \mbox{for} \quad k=1,2,\ldots , n. \]
This means that in each row of the matrix the magnitude of the element on the main diagonal must exceed the sum of the magnitudes of all other elements in the row. ■

Theorem (Jacobi iteration): Suppose that A is a strictly diagonally dominant matrix. Then A x = b has a unique solution x = p. Iteration using Jacobi formula

\[ x_j^{(k+1)} = \frac{1}{a_{j,j}} \left[ b_j - a_{j,1} x_1^{(k)} - \cdots - a_{j,j-1} x_{j-1}^{(k)} - a_{j,j+1} x_{j+1}^{(k)} - \cdots - a_{j,n} x_n^{(k)} \right] , \quad j=1,2,\ldots , n , \]
will produce a sequence of vectors \( \left\{ {\bf p}_k \right\}_{k\ge 0} \) that will converge to p for any choice of the starting vector p0. ■

Seidel Method

Gauss-Seidel method is used to solve a set of simultaneous linear and nonlinear equations, A x = b, where \( {\bf A} = \left[ a_{i,j} \right] \) is a square \( n \times n \) matrix, x is unknown n-vector, and b is a given n-vector. If b depends on x, we will write it as \( {\bf b} = {\bf f} ({\bf x}) . \) We consider first the case when b is a given vector not depending on x.

Example: The system of equations

\[ \begin{split} 4x-2y+z&=9, \\ 2x+8y-3z&=19, \\ x+2y -5z&=2. \end{split} \]
can be iterated as follows:
\[ \begin{split} x_{k+1}&= (9+2y_k -z_k )/4 , \\ y_{k+1}&=(19-2x_{k+1} +3z_k )/8 , \\ z_{k+1}&=(x_{k+1} +2y_{k+1} -2)/5. \end{split} \]
x[0] = 2; y[0] = 1; z[0] = 0; xp = x[0]; yp = y[0]; zp = z[0];
Do[{{xp = N[(9 + 2 y[k] - z[k])/4], yp = N[(19 - 2 xp + 3 z[k])/8],
zp = N[(xp + 2 yp - 2)/5]}, {x[k + 1] = xp, y[k + 1] = yp, z[k + 1] = zp}}, {k, 0, 10}]
Do[Print["i=", i, " x= ", x[i], " y= ", y[i], " z= ", z[i]], {i, 0, 10}]
■
It seems reasonable that xk+1 could be used in place of xk in the computations of yk+1 and zk+1. Similarly, yk+1 might be used in computation of zk+1. Such algorithm, also known as the Liebmann method or the method of successive displacement, is named after the German mathematicians Carl Friedrich Gauss (1777--1855) and Philipp Ludwig von Seidel (1821--1896). This algorithm was only mentioned in a private letter from Gauss to his student Gerling in 1823. A publication was not delivered before 1874 by Seidel, who also discovered in 1847 the crucial analytic concept of uniform convergence. In 1857, von Seidel decomposed the first order monochromatic aberrations into five constituent aberrations. They are now commonly referred to as the five Seidel Aberrations. The lunar crater Seidel is named after him. The following table confirms that with Gauss-Seidel ietration converges faster than Jacobi.

If we start with \( {\bf p}_0 = (2,1,0) , \) then iteration will converge to the solution (3,2,1) much faster than under Jacobi method.
k  x_k  y_k  z_k 
0  2  1  0 
1  2.75  1.6875  0.825 
2  2.8875  1.9625  0.9625 
3  2.99063  1.98828  0.993438 
4  2.99578  1.99859  0.998594 
5  2.99965  1.99956  0.999754 
6  2.99984  1.99995  0.999947 
7  2.99999  1.99995  0.999947 
8  2.99999  1.99998  0.999991 
9  3.  2.  1. 
10  3.  2.  1. 

The linear equation A x = b can be rewritten as

\[ x_i = \frac{1}{a_{i,i}} \left( b_i - \sum_{j=1, \ j\ne i}^n a_{i,j} b_j \right) , \quad\mbox{for}\quad i =1,2,\ldots n. \]
In certain cases, such as when a system of equations is large, iterative methods of solving equations such as Gauss-Seidel method are more advantageous. Elimination methods, such as Gaussian Elimination, are prone to round-off errors for a large set of equations whereas iterative methods, such as Gauss-Seidel method, allow the user to control round-off error. Also if the physics of the problem are well known, initial guesses needed in iterative methods can be made more judiciously for faster convergence.

The following are the input parameters to begin the simulation. The user can change those values that are highlighted and the worksheet will calculate an approximate solution to the system of equations.

Below, maxit iterations are conducted and values of the previous approximations, present approximations, absolute relative approximate error, and maximum absolute relative approximate error are calculated at the end of each iteration.
absea = Array[0, n];
Print[" "]
For[k = 1, k <= maxit, k++,
Print["Iteration Number"];
Print[k];
Print["Previous iteration values of the solution vector"];
Xold = x;
Print[Xold];
For[i = 1, i <= n, i++, summ = 0;
For[j = 1, j <= n, j++,
If[i != j, summ = summ + A[[i, j]]*x[[j]]]];
x[[i]] = N[(RHS[[i]] - summ)/A[[i, i]]]];
Maxabsea = 0.0;
For[i = 1, i <= n, i++,
absea[[i]] = Abs[(x[[i]] - Xold[[i]])/x[[i]]]*100.0;
If[absea[[i]] > Maxabsea, Maxabsea = absea[[i]]]];
Print["New iterative values of the solution vector"];
Print[x];
Print["Absolute percentage relative approximate error"];
Print[absea];
Print["Maximum absolute percentage relative approximate error"];
Print[Maxabsea];
Print[" "]; Print["__________________________________________"]; Print[" "];]
The last iteration above generates an approximate value with the given number of maximum iterations. The exact answer can be found by using Mathematica's built-in tools. The exact answer, last iterative solution vector, absolute relative true error (abset), maximum absolute relative true error (maxabset), and maximum absolute relative approximate error are given below.
B = LinearSolve[A, RHS];
abset = Array[0, n];
Maxabset = 0.0;
For[i = 1, i <= n, i++, abset[[i]] = Abs[(B[[i]] - x[[i]])/B[[i]]]*100.0;
If[Maxabset <= abset[[i]], Maxabset = Abs[abset[[i]]]]];
Print["Exact Answer"]
Print[B]
Print[" "]; Print["_______________________________________"]; Print[" "];
Print["Last Iterative Value"]
Print[x]
Print[" "]; Print["_______________________________________"]; Print[" "];
Print["Absolute percentage relative true error"]
Print[abset]
Print[" "]; Print["_______________________________________"]; Print[" "];
Print["Maximum absolute percentage relative true error"]
Print[Maxabset]
Print[" "]; Print["_______________________________________"]; Print[" "];
Print["Maximum absolute percentage relative approximate error"]
Print[Maxabsea]

 

Wegstein Algorithm

In 1958, J.H. Wegstein proposed (Comm ACM, 1, 9, 1958) another method for solving

 

We extend the methods studied previously to the case of systems of nonlinear equations. Let us start with planar case and consider two functions
\[ f(x,y) = x^2 - 2*x - y + 1, \qquad g(x,y) = x^2 + 9*y^2 - 9 . \]
We seek a method of solution for the system of nonlinear equations
\[ f(x,y) = 0, \qquad g(x,y) = 0 . \]
By plotting implicitly these two curves, we see that the given system of equations has two roots: (0,1) and (1.88241, 0.778642).
a = Plot[y /. Solve[x^2 - 2*x - y + 1 == 0], {x, -4, 4}, AspectRatio -> 1]
b = Plot[y /. Solve[x^2 + 9*y^2 - 9 == 0], {x, -4, 4}, AspectRatio -> 1]
Show[a, b, PlotRange -> {-0.5, 1.5}]
or
ContourPlot[x^2 - 2*x - y + 1 == 0, {x, -5, 5}, {y, -3, 3}, AspectRatio -> Automatic]
NSolve[{x^2 + 9*y^2 - 9 == 0, x^2 - 2*x - y + 1 == 0}, {x, y}]

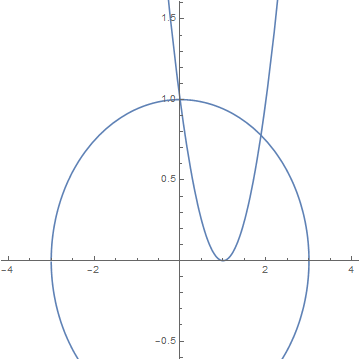
Fixed Point Iteration

We consider the problem \( {\bf x} = {\bf g} \left( {\bf x} \right) , \) where \( {\bf g}: \, \mathbb{R}^n \mapsto \mathbb{R}^n \) is the function from n-dimensional space into the same space. The fixed-point iteration is defined by selecting a vector \( {\bf x}_0 \in \mathbb{R}^n \) and defining a sequence \( {\bf x}_{k+1} = {\bf g} \left( {\bf x}_k \right) , \quad k=0,1,2,\ldots . \)

A point \( {\bf x} \in \mathbb{R}^n \) is a fixed point of \( {\bf g} \left( {\bf x} \right) \) if and only if \( {\bf x} = {\bf g} \left( {\bf x} \right) . \) A mapping \( {\bf f} \left( {\bf x} \right) \) is a contractive mapping if there is a positive number L less than 1 such that

\[ \left\| {\bf f} \left( {\bf x} \right) - {\bf f} \left( {\bf y} \right) \right\| \le L\, \| {\bf x} - {\bf y} \| , \qquad 0 < L < 1 . \]

Theorem: Let \( {\bf g} \left( {\bf x} \right) \) be a continuous function on \( \Omega = \left\{ {\bf x} = (x_1 , x_2 , \ldots x_n ) \, : \ a_i < x_i < b_i \right\} \) such that

  • \( {\bf g} \left( \Omega \right) \subset \Omega ; \)
  • \( {\bf g} \left( {\bf x} \right) \) is a contraction.
Then
  • g has a fixed point \( {\bf x} \in \Omega \) and the sequence \( {\bf x}_{k+1} = {\bf g} \left( {\bf x}_k \right) , \quad k=0,1,2,\ldots ; \quad {\bf x}_0 \in \Omega \) converges to x;
  • \( \| {\bf x}_k - {\bf x} \| \le L^k \,\| {\bf x}_0 - {\bf x} \| . \) ■

Example:

Example. We apply the fixed point iteration to find the roots of the system of nonlinear equations

\[ f(x,y) = x^2 - 2\,x - y + 1 =0, \qquad g(x,y) = x^2 + 9\,y^2 - 9 =0. \]
The first equation can be used to solve for either x or y. Depending on our choice, we can add either 18y or 2x to the second equation. So we have two formulas for iteration:
\[ \begin{cases} x &= \frac{1}{2} \left[ x^2 -y+1 \right] , \\ y &= \frac{1}{18} \left[ x^2 + 9\,y^2 -9 + 18\,y \right] , \end{cases} \qquad\mbox{or} \qquad \begin{cases} y &= \left( x -1 \right)^2 , \\ x &= \frac{1}{2} \left[ (x+1)^2 + 9\,y^2 -10 \right] . \end{cases} \]
These two system of equations are used to write the recursive formulas. Start with an initial point (0,0.5), and then compute the sequence \( \left\{ (x_k , y_k ) \right\} \) according to the formula:
\[ \begin{cases} x_{k+1} &= \frac{1}{2} \left[ x^2_k -y_k +1 \right] , \\ y_{k+1} &= \frac{1}{18} \left[ x^2_k + 9\,y^2_k -9 + 18\,y \right] . \end{cases} \]
Then we repeat calculations according to the second formula:
\[ \begin{cases} y_{k+1} &= \left( x_k -1 \right)^2 , \\ x_{k+1} &= \frac{1}{2} \left[ (x_k +1)^2 + 9\,y_k^2 -10 \right] . \end{cases} \]
x[0] = 0; y[0] = 0.5;
Do[{x[k + 1] = N[(x[k]^2 - y[k] + 1)/2], y[k + 1] = N[(x[k]^2 + 9*y[k]^2 - 9 + 18*y[k])/18]}, {k, 0, 50}]
Do[Print["i=", i, " x= ", x[i], " y= ", y[i]], {i, 0, 10}]
x[0] = 0; y[0] = 0.5;
Do[{y[k + 1] = N[(x[k] - 1)^2], x[k + 1] = N[((x[k] + 1)^2 + 9*y[k]^2 - 10)/2]}, {k, 0, 10}]
Do[Print["i=", i, " x= ", x[i], " y= ", y[i]], {i, 0, 10}]
We summarize the results of computations in the table
k  x_k  y_k    k  x_k  y_k 
0  0  0.5    0  0  0.5 
1  0.25  0.125    1  -3.375  1 
2  0.46875  -0.363715    2  2.32031   19.1406 
3  0.791721  -0.785364    3  1649.15  1.74323 
4  1.20609  -0.942142    4  1.3615*1010  2.71639*106 
5  1.6984  -0.917512    5  3.41314*1013  1.85369*1012 
6  2.40104  -0.836344    6  5.97938*1026  1.16495*1027 
7  3.80067  -0.666331         
8  8.0557  -0.141829         
9  33.0181  2.9734         
So we see that both sequences diverge from the fixed point (0,1).

If we use the starting value (1.5, 0.5), then

k  x_k  y_k    k  x_k  y_k 
0  1.5  0.5    0  1.5  0.5 
1  1.375  0.25    1  -0.75  0.25 
2  1.32031  -0.113715    2  -4.6875  3.0625 
3  1.42847  -0.510404    3  44.0039  32.3477 
4  1.77547  -0.766785    4  5716.34  1849.34 
5  2.45953  -0.797679    5  3.17342056*107  3.26652*107 
6  3.92349  -0.643461    6  5.3050884*1015  1.00706*1015 
7  8.5186  -0.0812318    7  1.86357*1031  2.8144*1031 
8  36.8239  3.45355    8     
9  676.774  84.2505    9     
So both sequences diverge. ■

We want to determine why our iterative equations were not suitable for finding the solution near both fixed points (0, 1) and (1.88241, 0.778642). To answer this question, we need to evaluate the Jacobian matrix:

\[ {\bf J} (x,y) = \begin{bmatrix} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} \\ \frac{\partial g}{\partial x} & \frac{\partial g}{\partial y} \end{bmatrix} . \]

Theorem: Assume that the functions f(x,y) and g(x,y) and their first partial derivatives are continuous in a region that contain the fixed point (p,q). If the starting point is chosen sufficiently close to the fixed point and if

\[ \begin{cases} \left\vert \frac{\partial f}{\partial x}(p,q) \right\vert + \left\vert \frac{\partial f}{\partial y}(p,q) \right\vert < 1, \\ \left\vert \frac{\partial g}{\partial x}(p,q) \right\vert + \left\vert \frac{\partial g}{\partial y}(p,q) \right\vert < 1, \end{cases} \]
then the iteration
\[ x_{k+1} = f(x_k , y_k ) , \qquad y_{k+1} = g(x_k , y_k ) , \qquad k=0,1,2,\ldots ; \]
converges to the fixed point (p,q). ■

Seidel Method

An improvement analogous to the Gauss-Seiel method for linear systems, of fixe-point iteration can be made. Suppose we try to solve the system of two nonlinear equations
\[ x = f(x,y) , \qquad y= g(x,y) . \]
Staring with some initial point \( (x_0 , y_0 ) , \) we compute the sequence according to the following formulas, called Seidel method:
\[ x_{k+1} = f(x_k ,y_k ) , \qquad y_{k+1} = g(x_{k+1} ,y_k) , \qquad k=0,1,2,\ldots . \]

Wegstein Algorithm

Let \( {\bf g} \, : \, \mathbb{R}^n \mapsto \mathbb{R}^n \) be a continuous function. Suppose we are given a system of equations

\[ \begin{split} x_1 &= g_1 \left( x_1 , x_2 , \ldots , x_n \right) , \\ x_2 &= g_2 \left( x_1 , x_2 , \ldots , x_n \right) , \\ \vdots & \qquad \vdots \\ x_n &= g_n \left( x_1 , x_2 , \ldots , x_n \right) . \end{split} \]
Then Wegstein iteration equations can we written as
\[ \begin{split} x_1^{(k+1)} &= q_1 x_1^{(k)} + \left( 1- q_1 \right) g_1 \left( x_1^{(k)} , x_2^{(k)} , \ldots , x_n^{(k)} \right) , \\ x_2^{(k+1)} &= q_2 x_2^{(k)} + \left( 1- q_2 \right) g_2 \left( x_1^{(k)} , x_2^{(k)} , \ldots , x_n^{(k)} \right) , \\ \vdots & \qquad \vdots \\ x_n^{(k+1)} &= q_n x_n^{(k)} + \left( 1- q_n \right) g_n \left( x_1^{(k)} , x_2^{(k)} , \ldots , x_n^{(k)} \right) , \end{split} \]
where
\[ q_i = \dfrac{\partial g_i / \partial x_i}{\partial g_i / \partial x_i -1} \qquad\mbox{evaluated at} \quad \left( x_1^{(k)} , x_2^{(k)} , \ldots , x_n^{(k)} \right) , \qquad i=0,1,2,\ldots n; \]
Here again k denotes the number of the iteration.

In planar case, we have two equations

\[ x= f(x,y), \qquad y= g(x,y) . \]
The Wegstein iterations become
\[ \begin{cases} X_{k+1} &= q_1 X_k + \left( 1-q_1 \right) f\left( X_k , Y_k \right) , \\ Y_{k+1} &= q_2 Y_k + \left( 1-q_2 \right) g\left( X_k , Y_k \right) , \end{cases} \]
where
\[ q_1 = \frac{f_x}{f_x -1} , \qquad q_2 = \frac{g_y}{g_y -1} \]
are evaluated at the point \( \left( x_k , y_k \right) . \) Then
\[ \begin{cases} x_{k+1} &= q_1 x_k + \left( 1-q_1 \right) f\left( X_{k+1} , Y_{k+1} \right) , \\ y_{k+1} &= q_2 y_k + \left( 1-q_2 \right) g\left( X_{k+1} , Y_{k+1} \right) , \qquad k=0,1,2,\ldots . \end{cases} \]
A condition for Wegstein algorithm to be stable at a root is
\[ \left\vert \frac{f_x \,g_y}{\left( f_x -1 \right)\left( g_y -1 \right)} \right\vert < 1 . \]

Example:

Example. We apply the Wegstein algorithm to find the roots of the system of nonlinear equations

\[ x^2 - 2\,x - y + 1 =0, \qquad x^2 + 9\,y^2 - 9 =0. \]
By adding and subtracting x and y from each equation, respectively, we reduce the given problem to fixed point system of equations:
\[ x= f(x,y) = x^2 - x - y + 1 , \qquad y = g(x,y) = x^2 + 9\,y^2 - 9 +y . \]
We know that such system of equations has two real fixed points (0,1) and (1.88241, 0.778642). Their partial derivatives are \( f_x = 2x-1 \) and \( g_y = 18\,y +1 . \) At the first fixed point (0,1) we have
\[ \left\vert \frac{f_x \,g_y}{\left( f_x -1 \right)\left( g_y -1 \right)} \right\vert_{x=0, y=1} = \frac{19}{36} < 1 , \]
while at the another point (1.88241, 0.778642) its value is
\[ \left\vert \frac{f_x \,g_y}{\left( f_x -1 \right)\left( g_y -1 \right)} \right\vert_{x=1.88241, y=0.778642} = 1.67841 > 1 . \]
So we expect that the sequence of Wegstein iterations will converge to the fixed point (0,1), but it will diverge from another fixed point (1.88241, 0.778642). ■

Newton's Methods

The Newton methods have problems with the initial guess which, in general, has to be selected close to the solution. In order to avoid this problem for scalar equations we combine the bisection and Newton's method. First, we apply the bisection method to obtain a small interval that contains the root and then finish the work using Newton’s iteration.

For systems, it is known the global method called the descent method of which Newton’s iteration is a special case. Newton’s method will be applied once we get close to a root.

Let us consider the system of nonlinear algebraic equations \( {\bf f} \left( {\bf x} \right) =0 , \) where \( {\bf f} \,:\, \mathbb{R}^n \mapsto \mathbb{R}^n , \) and define the scalar multivariable function

\[ \phi ({\bf x}) = \frac{1}{2}\, \sum_{i=1}^n f_i^2 ({\bf x} ) = \frac{1}{2}\,{\bf f}^T \,{\bf f} \]
The function φ has the following properties.
  • \( \phi ({\bf x}) \ge 0 \) for all \( {\bf x} \in \mathbb{R}^n . \)
  • If x is a solution of \( {\bf f} \left( {\bf x} \right) =0 , \) then φ has a local minimum at x.
  • At an arbitrary point x0, the vector \( - \nabla \phi ({\bf x}_0 ) \) is the direction of the most rapid decrease of φ.
  • φ has infinitely many descent directions.
  • A direction u is descent direction for φ at x if and only if \( {\bf u}^T \nabla \phi ({\bf x}) < 0 . \)
  • Special descent directions:
    (a) Steepest descent method: \( {\bf u}_k = -JF^T ({\bf x}_k )\, {\bf f} ({\bf x}_k ) , \)
    (b) Newton’s method: \( {\bf u}_k = -JF^{-1} ({\bf x}_k )\, {\bf f} ({\bf x}_k ) . \) ■

For scalar problems \( f (x) =0 , \) the descent direction is given by \( - \phi' (x) = -2\,f(x) \,f' (x) \) while Newton’s method yields \( -f(x) / f' (x) \) which has the same sign as the steepest descent method.

The question that arises for all descent methods is how far should one go in a given descent direction. To answer this question, there are several techniques and conditions to guarantee convergence to a minimum of φ. For a detailed discussion consult the book by

Numerical Methods for Unconstrained Optimization and Nonlinear Equations, by J. E. Dennis, Jr. and Robert B. Schnabel. Published: 1996, ISBN: 978-0-89871-364-0
http://www.math.vt.edu/people/adjerids/homepage/teaching/F09/Math5465/chapter2.pdf

 

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions