Return to computing page for the second course APMA0340
Return to computing page for the fourth course APMA0360
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to Mathematica tutorial for the fourth course APMA0360
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to the main page for the fourth course APMA0360
Return to Part VII of the course APMA0340
Introduction to Linear Algebra with Mathematica
Glossary
Preface
This section presents applications of Legendre polynomials for solving Laplace's equation in spherical coordinates.
Laplace's equation in spherical coordinates
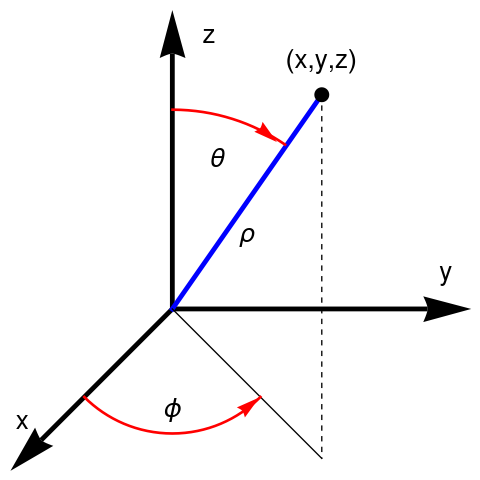
Let us introduce in ℝ³ spherical coordinates (0 ≤ ρ, 0 ≤ θ < π, 0 ≤ ϕ < 2π):
\[
\begin{split}
x &= \rho\,\cos \phi\,\sin\theta , \\
y &= \rho\,\sin \phi\,\sin\theta , \\
z &= \rho\,\cos\theta ;
\end{split} \qquad \Longrightarrow \qquad \phi = \begin{cases}
\arctan \left( y/x \right) , & \ \mbox{ if} \quad x > 0 , \\
\arctan \left( y/x \right) + \pi , & \ \mbox{ if} \quad x < 0 \mbox{ and } y \ge 0, \\
\arctan \left( y/x \right) - \pi , & \ \mbox{ if} \quad x < 0 \mbox{ and } y < 0, \\
+\frac{\pi}{2} , & \ \mbox{ if} \quad x = 0 \mbox{ and } y > 0, \\
-\frac{\pi}{2} , & \ \mbox{ if} \quad x = 0 \mbox{ and } y < 0, \\
\mbox{undefined}, & \ \mbox{ if} \quad x = 0 \mbox{ and } y=0.
\end{cases} .
\]
As usual, the location of a point (x, y, z) is specified by the distance ρ of the point from the origin, the angle ϕ between the position vector and the z-axis, the polar angle measured down from the north pole, and the azimuthal angleq θ from the x-axis to the projection of the position vector onto the xy plane, analogous to longitude in earth measuring coordinates:
\[
\rho = \sqrt{x^2 + y^2 + z^2} \ge 0 \qquad\mbox{and} \qquad \theta = \mbox{arccos} \frac{z}{\rho} = \begin{cases}
\arctan \frac{\sqrt{x^2 + y^2}}{z} , & \mbox{ if } z > 0, \\
\pi + \arctan \frac{\sqrt{x^2 + y^2}}{z} , & \mbox{ if } z < 0, \\
+ \frac{\pi}{2} , & \mbox{ if } z = 0 \mbox{ and } xy \ne 0 , \\
\mbox{undefined} , & \mbox{ i } x=y=z=0 .
\end{cases}
\]
|
az = Graphics[{Black, Thickness[0.01], Arrowheads[0.1],
Arrow[{{0, 0}, {0, 1.2}}]}];
ax = Graphics[{Black, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {-0.65, -0.65}}]}]; ay = Graphics[{Black, Thickness[0.01], Arrowheads[0.1], Arrow[{{0, 0}, {1.2, 0}}]}]; line = Graphics[{Blue, Thickness[0.01], Line[{{0, 0}, {0.6, 0.86}}]}]; line1 = Graphics[{Black, Dashed, Line[{{0.6, 0.86}, {0.6, -0.6}}]}]; line2 = Graphics[{Black, Line[{{0, 0}, {0.6, -0.6}}]}]; circle1 = Graphics[{Red, Thick, Circle[{0, 0}, 0.8, {Pi/2, 0.97}]}]; circle2 = Graphics[{Red, Thick, Circle[{0, 0}, 0.5, {-Pi/4, -3*Pi/4}]}]; ar1 = Graphics[{Red, Arrowheads[0.05], Arrow[{{0.36, 0.72}, {0.42, 0.67}}]}]; ar2 = Graphics[{Red, Arrowheads[0.05], Arrow[{{0.3, -0.395}, {0.35, -0.355}}]}]; disk = Graphics[Disk[{0.6, 0.86}, 0.03]]; tx = Graphics[{Black, Text[Style["x", 20], {-0.6, -0.45}]}]; ty = Graphics[{Black, Text[Style["y", 20], {1.1, 0.15}]}]; tz = Graphics[{Black, Text[Style["z", 20], {0.15, 1.1}]}]; tf = Graphics[{Black, Text[Style[\[Phi], 20], {0.18, 0.6}]}]; tt = Graphics[{Black, Text[Style[\[Theta], 20], {0, -0.4}]}]; tp = Graphics[{Black, Text[Style["(x,y,z)", 20], {0.6, 1.0}]}]; tr = Graphics[{Black, Text[Style[\[Rho], 20], {0.3, 0.3}]}]; Show[ax, ay, az, line, line1, line2, circle1, circle2, ar1, ar2, \ disk, tx, ty, tz, tf, tt, tp, tr] |
|
| Spherical coordinates. | Mathematica code |
The Laplace's equation Δu = 0 in spherical coordinates (ρ θ ϕ) can be written as
\begin{equation} \label{EqSphere.1}
\nabla^2 u = \frac{1}{\rho^2} \,\frac{\partial}{\partial \rho} \left( \rho^2 \frac{\partial u}{\partial \rho} \right) + \frac{1}{\rho^2 \sin \phi} \,\frac{\partial}{\partial \phi} \left( \sin\phi \,\frac{\partial u}{\partial\phi} \right) + \frac{1}{\rho^2 \sin^2 \phi} \,\frac{\partial^2 u}{\partial \theta^2} = 0.
\end{equation}
We look for partial nontrivial (not identically zero) solutions of equation \eqref{EqSphere.1} that is represented as a product of two functions
\[
u(\rho , \theta , \phi ) = R(\rho )\, Y(\theta , \phi ) .
\]
Substituting this product-function into Eq.\eqref{EqSphere.1} and divide the result by u, we obtain
\[
\frac{1}{R(\rho )} \,\frac{\partial}{\partial \rho} \left( \rho^2 \frac{\partial R}{\partial \rho} \right) + \frac{1}{Y(\theta , \phi )} \left[ \frac{1}{\sin \phi} \,\frac{\partial}{\partial \phi} \left( \sin\phi \,\frac{\partial Y}{\partial\phi} \right) + \frac{1}{\sin^2 \phi} \,\frac{\partial^2 Y}{\partial \theta^2} \right] = 0.
\]
The first term in the left-hand side does not depend on angles (θ, ϕ). Therefore, the equation is valid only when every term is a constant:
\[
\frac{1}{R(\rho )} \,\frac{\partial}{\partial \rho} \left( \rho^2 \frac{\partial R}{\partial \rho} \right) = \lambda ,
\]
and
\[
\frac{1}{Y(\theta , \phi )} \left[ \frac{1}{\sin \phi} \,\frac{\partial}{\partial \phi} \left( \sin\phi \,\frac{\partial Y}{\partial\phi} \right) + \frac{1}{\sin^2 \phi} \,\frac{\partial^2 Y}{\partial \theta^2} \right] = -\lambda ,
\]
where λ is a constant. From these equations, it follows
\begin{equation} \label{EqSphere.2}
\rho^2 \frac{{\text d}^2 R}{{\text d}\rho^2} + 2\rho\,\frac{{\text d}R}{{\text d}\rho} - \lambda\,R(\rho ) = 0,
\end{equation}
and
\begin{equation} \label{EqSphere.3}
\frac{1}{\sin \phi} \,\frac{\partial}{\partial \phi} \left( \sin\phi \,\frac{\partial Y}{\partial\phi} \right) + \frac{1}{\sin^2 \phi} \,\frac{\partial^2 Y}{\partial \theta^2} + \lambda\, Y(\theta , \phi ) = 0.
\end{equation}
Eq.\eqref{EqSphere.3} can also be solved by separation of variables Y(θ, ϕ) = Θ(θ) Φ(ϕ), which leads to
\[
\frac{\Theta (\theta )}{\sin \phi} \,\frac{{\text d}}{{\text d} \phi} \left( \sin\phi \,\frac{{\text d}\Phi}{{\text d}\phi} \right) + \frac{\Phi (\phi )}{\sin^2 \phi} \,\frac{{\text d}^2 \Theta}{{\text d} \theta^2} + \lambda\, \Theta (\theta )\, \Phi(\phi ) = 0 \qquad \Longrightarrow \qquad - \lambda\,\sin^2 \phi - \frac{\sin\phi}{\Phi (\phi )} \,\frac{{\text d}}{{\text d} \phi} \left( \sin\phi \,\frac{{\text d}\Phi}{{\text d}\phi} \right) = \frac{1}{\Theta (\theta )} \,\frac{{\text d}^2 \Theta}{{\text d} \theta^2} .
\]
Since we separate variables, we get two equations
\[
\frac{1}{\Theta (\theta )} \,\frac{{\text d}^2 \Theta}{{\text d} \theta^2} = -\mu \qquad \Longrightarrow \qquad \frac{{\text d}^2 \Theta}{{\text d} \theta^2} + \mu \,\Theta (\theta ) = 0
\]
and
\[
\lambda\,\sin^2 \phi + \frac{\sin\phi}{\Phi (\phi )} \,\frac{{\text d}}{{\text d} \phi} \left( \sin\phi \,\frac{{\text d}\Phi}{{\text d}\phi} \right) = \mu \qquad \Longrightarrow \qquad \sin\phi\,\frac{{\text d}}{{\text d} \phi} \left( \sin\phi \,\frac{{\text d}\Phi}{{\text d}\phi} \right) - \left( \mu - \lambda\,\sin^2 \phi \right) \Phi (\phi ) = 0 .
\]
From the latter, we get a Sturm--Liouville problem
\[
\frac{{\text d}^2 \Theta}{{\text d} \theta^2} + \mu \,\Theta (\theta ) = 0 , \qquad \Theta (\theta ) = \Theta (\theta + 2 \pi ) ,
\]
with eigenvalues μ = m², for which correspond eigenfunctions are
\[
\Theta_m (\theta ) = a_m \cos m\theta + b_m \sin m\theta , \qquad m=0,1,2,\ldots .
\]
Here 𝑎m and bm are some real constants.
Substuting this value μ = m² into equation for Φ, we get the Sturm--Liouville problem
\[
\sin\phi\,\frac{{\text d}}{{\text d} \phi} \left( \sin\phi \,\frac{{\text d}\Phi}{{\text d}\phi} \right) + \left( \lambda\,\sin^2 \phi - m^2 \right) \Phi (\phi ) = 0, \qquad \Phi (0) < \infty , \quad \Phi (\pi ) < \infty .
\]
Upon making substitution x = cos(ϕ) and dividing by sin²(ϕ), we obtain a familiar
Sturm--Liouville problem
\[
\frac{\text d}{{\text d}x} \left( 1 - x^2 \right) \frac{{\text d}P(x)}{{\text d}x} + \left( \lambda - \frac{m^2}{1-x^2} \right) P(x) = 0 , \qquad P(-1) < \infty , \quad P(1) < \infty .
\]
The latter is a Sturm--Liouville problem for the associated Legendre polynomials and we find eigenvalues and corresponding eigenfunctions:
\[
\lambda_n = n(n+1) , \qquad P(x) = P_{n,m} (x) = P_n^m (x) , \qquad n=0,1,2,\ldots ,
\]
where Pn,m(x), also denoted by Pnm(x), are the associated Legendre polynomials.
With this in hand, we determine eigenvalues and eigenfunctions for equation
\eqref{EqSphere.3}:
\begin{equation} \label{EqSphere.4}
Y_{n,m} (\theta , \phi ) = P_n^m (\cos\theta ) \left[ a_m \cos m\phi + b_m \sin m\phi \right] , \qquad m=0,1,2,\ldots , n, \quad n=0,1,2,\ldots .
\end{equation}
These functions Yn,m(θ,
ϕ) are called spherical functions. These functions are orthogonal
\begin{equation} \label{EqSphere.5}
\iint_{\Sigma}
Y_{n,m} (\theta , \phi )\, Y_{i,j} (\theta , \phi )\, \sin\theta\,{\text d}\theta\,{\text d}\phi = 0 \qquad\mbox{if} \quad m\ne i \quad \mbox{or} \quad m \ne j .
\end{equation}
Using Mathematica, we find first ten spherical functions:
Series[1/Sqrt[1 - 2*x*t + t^2], {t, 0, 10}]
| n | m | Spherical function | ||
|---|---|---|---|---|
| n = 0 | m = 0 | Y0,0(θ, ϕ) = 1 | ||
| n = 1 | m = 0 | Y1,0(θ, ϕ) = cosθ | ||
| n = 1 | m = 1 | \( \displaystyle Y_{1,1} (\theta , \phi ) = -\sin \theta \left( a_1 \cos\phi + b_1 \sin\phi \right) \) | ||
| n = 2 | m = 0 | \( \displaystyle Y_{2,0} (\theta , \phi ) = \frac{1}{2} \left( 3 \cos^2 \theta -1 \right) \) | ||
| n = 2 | m = 1 | \( \displaystyle Y_{2,1} (\theta , \phi ) = -3\cos \theta\,\sin\theta \left[ a_1 \cos\phi + b_1 \sin\phi \right] \) | ||
| n = 2 | m = 2 | \( \displaystyle Y_{2,2} (\theta , \phi ) = 3\,\sin^2 \theta \left[ a_2 \cos 2\phi + b_2 \sin 2\phi \right] \) | ||
| n = 3 | m = 0 | \( \displaystyle Y_{3,0} (\theta , \phi ) = \frac{1}{2}\,\cos \theta \left( 5\cos^2 \theta - 3 \right) \) | ||
| n = 3 | m = 1 | \( \displaystyle Y_{3,1} (\theta , \phi ) = \frac{3}{2}\,\sin \theta \left( 1 - 5 \cos^2 \theta \right) \left[ a_1 \cos \phi + b_1 \sin \phi \right] \) | ||
| n = 3 | m = 2 | \( \displaystyle Y_{3,2} (\theta , \phi ) = 15\cos\theta \,\sin^2 \theta \left[ a_2 \cos 2\phi + b_2 \sin 2\phi \right] \) | ||
| n = 3 | m = 3 | \( \displaystyle Y_{3,3} (\theta , \phi ) = -15\,\sin^3 \theta \left[ a_3 \cos 3\phi + b_3 \sin 3\phi \right] \) | ||
| n = 4 | m = 0 | \( \displaystyle Y_{4,0} (\theta , \phi ) = \frac{1}{8} \left( 35\,\cos^4 \theta - 30\,\cos^2 \theta + 3 \right) \) | ||
| n = 4 | m = 1 | \( \displaystyle Y_{4,1} (\theta , \phi ) = \frac{5}{2}\,\cos \theta \,\sin\theta \left( 3 - 7 \cos^2 \theta \right) \left[ a_1 \cos \phi + b_1 \sin \phi \right] \) | ||
| n = 4 | m = 2 | \( \displaystyle Y_{4,2} (\theta , \phi ) = \frac{15}{2}\,\sin^2 \theta \left( 7\,\cos^2 \theta -1 \right) \left[ a_2 \cos 2\phi + b_2 \sin 2\phi \right] \) | ||
| n = 4 | m = 3 | \( \displaystyle Y_{4,3} (\theta , \phi ) = -105\,\cos\theta \,\sin^3 \theta \left[ a_3 \cos 3\phi + b_3 \sin 3\phi \right] \) | ||
| n = 4 | m = 4 | \( \displaystyle Y_{4,4} (\theta , \phi ) = 105\,\sin^4 \theta \left[ a_4 \cos 4\phi + b_4 \sin 4\phi \right] \) | ||
| n = 5 | m = 0 | \( \displaystyle Y_{5,0} (\theta , \phi ) = \frac{1}{8}\,\cos\theta \left( 63\,\cos^4 \theta - 70\,\cos^2 \theta + 15 \right) \) |
Since Eq.\eqref{EqSphere.2} is an Eiler's ordinary differential equation, the general solution of the radial equation becomes
\[
R(\rho ) = R_n (\rho ) = A_n \rho^{n} + B_n \rho^{-n-1} ,
\]
with some constants An and Bn. So partial nontrivial solutions of Laplace's equation are products of the radial solutions and spherical functions: \( \displaystyle u_{n,m} (\rho , \theta , \phi ) = R_n (\rho )\, Y_{n,m} (\theta , \phi ) . \) Since Laplace's equation is homogeneous, any sum of these partial solutions will be also solutions of Laplace's equation. Hence, we seek the solution of
Laplace's equation as infinte sum:
\begin{equation} \label{EqSphere.6}
u(\rho , \theta , \phi ) = \sum_{n\ge 0} R_n (\rho ) \sum_{m=0}^n
Y_{n,m} (\theta , \phi ) = \sum_{n\ge 0} \left[ A_n \rho^{n} + B_n \rho^{-n-1} \right] \sum_{m=0}^n P_n^m (\cos\theta ) \left( a_m \cos m\phi + b_m \sin m\phi \right) .
\end{equation}
In particular, if we seek a solution in a domain not containing the origin, then its solution can be expressedthrough spherical functions as
\begin{equation} \label{EqSphere.7}
u(\rho , \theta , \phi ) = \sum_{n\ge 0} \left( \frac{R}{\rho} \right)^{n+1} \sum_{m=0}^n
Y_{n,m} (\theta , \phi ) = \sum_{n\ge 0} \left( \frac{R}{\rho} \right)^{n+1} \sum_{m=0}^n P_n^m (\cos\theta ) \left( a_m \cos m\phi + b_m \sin m\phi \right) .
\end{equation}
When we seek a harmonic function in a domain containing the origin, it solution becomes
\begin{equation} \label{EqSphere.8}
u(\rho , \theta , \phi ) = \sum_{n\ge 0} \left( \frac{\rho}{R} \right)^{n} \sum_{m=0}^n
Y_{n,m} (\theta , \phi ) = \sum_{n\ge 0} \left( \frac{\rho}{R} \right)^{n} \sum_{m=0}^n P_n^m (\cos\theta ) \left( a_m \cos m\phi + b_m \sin m\phi \right) .
\end{equation}
Example 1:
Example 2:
Example 3: Let us consider the interior Neumann problem for a sphere of radius 2:
\[
\nabla^2 u = 0 \quad (\rho < 3) , \qquad \left. \frac{\partial u}{\partial \rho} \right\vert_{\rho =3} = f(\theta , \phi ) .
\]
Example 4: Let us consider the outer Neumann problem for a sphere of radius 2:
\[
\nabla^2 u = 0 \quad (\rho > 2) , \qquad \left. \frac{\partial u}{\partial \rho} \right\vert_{\rho =2} = f(\theta , \phi ) .
\]
Accoding to formula \eqref{EqSphere.6}, we seek solution of the given boundary value problem in the form
\[
u(\rho , \theta , \phi ) = \sum_{n\be 0} \rho^{-n-1} \sum_{m=0}^n P_n^m (\cos\theta ) \left( a_m \cos m\phi + b_m \sin m\phi \right) .
\]
End of Example 2
Axisymmetric Laplace's equation in spherical coordinates
In case of axisymmetric solutions, Eq.\eqref{EqSphere.1} becomes
\begin{equation} \label{EqSphere.9}
\nabla^2 u = \frac{1}{\rho^2} \,\frac{\partial}{\partial \rho} \left( \rho^2 \frac{\partial u}{\partial \rho} \right) + \frac{1}{\rho^2 \sin \phi} \,\frac{\partial}{\partial \phi} \left( \sin\phi \,\frac{\partial u}{\partial\phi} \right) = 0.
\end{equation}
According to separation of variables method, we seek for partial nontrivial solutions of Eq.\eqref{EqSphere.7} in te form u(ρ, ϕ) = R(ρ)Φ(ϕ). Upon substiting this form into Eq.\eqref{EqSphere.7}, we obtain
\[
\Phi (\phi ) \,\frac{\text d}{{\text d} \rho} \left( \rho^2 \frac{{\text d} R(\rho )}{{\text d} \rho} \right) + \frac{R(\rho )}{\sin \phi} \,\frac{\text d}{{\text d} \phi} \left( \sin\phi \,\frac{{\text d} \Phi (\phi )}{{\text d}\phi} \right) = 0 \qquad \Longrightarrow \qquad
\frac{1}{R} \,\frac{\text d}{{\text d} \rho} \left( \rho^2 \frac{{\text d} R(\rho )}{{\text d} \rho} \right) - \frac{1}{\Phi (\phi )\,\sin \phi} \,\frac{\text d}{{\text d} \phi} \left( \sin\phi \,\frac{{\text d} \Phi (\phi )}{{\text d}\phi} \right) = -\lambda .
\]
A function of one independent variable (ρ) can be equal to another function of independent avriable ϕ only when both functions are constant. This yields two equations containing a parameter λ:
\[
\rho^2 \frac{{\text d}^2 R}{{\text d}\rho^2} + 2\rho\,\frac{{\text d}R}{{\text d}\rho} - \lambda\,R(\rho ) = 0,
\tag{\ref{EqSphere.2}}
\]
and
\begin{equation} \label{EqSphere.10}
\frac{1}{\sin \phi} \,\frac{\partial}{\partial \phi} \left( \sin\phi \,\frac{\partial \Phi}{\partial\phi} \right)
+ \lambda\, \Phi (\phi ) = 0 , \qquad \Phi (0) < \infty , \quad \Phi (\pi /2) < \infty .
\end{equation}
Sturm--Liouville problem \eqref{EqSphere.8} is a particular case of \eqref{EqSphere.3}; so we conclude that λ = n(n +1) , n = 0, 1, 2, …, are its eigenvalues and the corresponding eigenfunctions are
\[
\Phi_n (\phi ) = P_n (\cos\phi ) , \qquad n=0,1,2,\ldots .
\]
- Clenshaw, C.W., Norton, H.J.: The solution of nonlinear ordinary differential equations in chebyshev series. The Computer Journal, 1963, {\bf 6}, Issue 1, 88–92; https://doi.org/10.1093
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions