Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part I of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

Preface

This section provides the general introduction to

Bessel functions of second kind

 

Bessel function of second kind

The Bessel function of the second kind of order ν is defined as follows: \[ Y_{\nu} (x) = \frac{\cos \nu \pi \, J_{\nu} (x) - J_{-\nu} (x)}{\sin \nu \pi} . \]
This function is called either after Heinrich Martin Weber (1875--1913), who introduced Yν(x) in 1873, or after Carl Neumann (1832--1925), with notation Nν(x). Since there is no standard notation, we will distinguish them by defining the Neumann function N∋(x) = πY∋(x) as π multiple of the Weber function:
\[ N_{\nu} (x) = \pi\,Y_{\nu} (x) . \]
These functions are clearly solutions of the Bessel equation, as they are linear combinations of Bessel functions of the first kind. However, if ν is an integer, then Y∋(x), as defined, is the indeterminate form 0/0. Therefore, we need to use l’Hospital’s Rule to determine whether the limit as ν approaches an integer n is nonzero, so that we can obtain a meaningful solution.

Applying l’Hospital’s Rule yields

\[ \begin{split} Y_{\nu} (x) &= \lim_{\nu \to n} \,\frac{\cos \nu \pi \, J_{\nu} (x) - J_{-\nu} (x)}{\sin \nu \pi} \\ &= \lim_{\nu \to n} \,\frac{-\pi\,\sin \nu\pi \,J_{\nu} (x) + \cos \nu \pi \, \frac{\text d}{{\text d}\nu} \, J_{\nu} (x) - \frac{\text d}{{\text d}\nu} \, J_{-\nu} (x)}{\pi\,\cos \nu\pi} \\ &= \lim_{\nu \to n} \,\frac{1}{\pi} \left[ \frac{\text d}{{\text d}\nu} \, J_{\nu} (x) - \frac{\text d}{{\text d}\nu} \, J_{-\nu} (x) \right] . \end{split} \]
Using the series definition of the Bessel function of the first kind,
\[ J_{\nu} (x) = \sum_{k\ge 0} \frac{(-1)^k}{k!\,\Gamma (k+\nu +1)} \left( \frac{x}{2} \right)^{2k+\nu} , \]
as well as the digamma function
\[ \psi (x) = \frac{\text d}{{\text d}x}\, \ln \Gamma (x) = \frac{\Gamma' (x)}{\Gamma (x)} , \]
we obtain
\[ \begin{split} Y_{n} (x) &= \frac{1}{\pi} \left[ \sum_{k\ge 0} \frac{(-1)^k}{k! \, (k+n)!} \left( \frac{x}{2} \right)^{2k+n} \ln \left( \frac{x}{2} \right) + (-1)^n \sum_{k\ge 0}\frac{(-1)^k}{k! \, (k-n)!} \left( \frac{x}{2} \right)^{2k-n} \ln \left( \frac{x}{2} \right) \right] \\ & \quad - \frac{1}{\pi} \left[ \sum_{k\ge 0} \frac{(-1)^k \Gamma' (k+n+1)}{k! \,(k+n)!^2} \left( \frac{x}{2} \right)^{2k+n} + (-1)^n \sum_{k\ge 0} \frac{(-1)^k \Gamma' (k-n+1)}{k! \,(k-n)!^2} \left( \frac{x}{2} \right)^{2k-n} \right] \\ &= \frac{1}{\pi} \left[ J_n (x)\, \ln \left( \frac{x}{2} \right) + (-1)^n J_{-n} (x)\, \ln \left( \frac{x}{2} \right) \right] \\ & \quad - \frac{1}{\pi} \left[ \sum_{k\ge 0} \frac{(-1)^k \psi (k+n+1)}{k!\,(k+n)!} \left( \frac{x}{2} \right)^{2k+n} + (-1)^n \sum_{k\ge 0} \frac{(-1)^k \psi (k+n+1)}{k!\,(k-n)!} \left( \frac{x}{2} \right)^{2k-n} \right] \\ &= \frac{2}{\pi} \, J_n (x)\, \ln \left( \frac{x}{2} \right) \\ & \quad - \frac{1}{\pi} \left[ \sum_{k\ge 0} \frac{(-1)^k \psi (k+n+1)}{k!\,(k+n)!} \left( \frac{x}{2} \right)^{2k+n} + (-1)^n \sum_{k\ge -n} \frac{(-1)^{k+n} \psi (k+1)}{k!\,(k+n)!} \left( \frac{x}{2} \right)^{2k+n} \right] \\ &= \frac{2}{\pi} \, J_n (x)\, \ln \left( \frac{x}{2} \right) - \frac{(-1)^n}{\pi} \,\sum_{k=-n}^{-1} \frac{(-1)^k \psi (k+1)}{k!\,(k+n)!} \left( \frac{x}{2} \right)^{2k+n} \\ & \quad - \frac{1}{\pi} \sum_{k\ge 0} \frac{(-1)^k}{k! \,(k+n)!} \left( \frac{x}{2} \right)^{2k+n} \left[ \psi (k+n+1) + \psi (k+1) \right] \\ &= \frac{2}{\pi} \, J_n (x)\, \ln \left( \frac{x}{2} \right) - \frac{(-1)^n}{\pi} \,\sum_{k=0}^{n-1} \frac{(-1)^k \psi (k-n+1)}{k!\,(k-n)!} \left( \frac{x}{2} \right)^{2k-n} \\ & \quad - \frac{1}{\pi} \sum_{k\ge 0} \frac{(-1)^k}{k! \,(k+n)!} \left( \frac{x}{2} \right)^{2k+n} \left[ \psi (k+n+1) + \psi (k+1) \right] \\ &= \frac{2}{\pi} \, J_n (x)\, \ln \left( \frac{x}{2} \right) - \frac{1}{\pi} \,\sum_{k=0}^{n-1} \frac{(n-k-1)!}{k!} \left( \frac{x}{2} \right)^{2k-n} \\ & \quad - \frac{1}{\pi} \sum_{k\ge 0} \frac{(-1)^k}{k!\, (k+n)!} \left( \frac{x}{2} \right)^{2k+n} \left[ \psi (k+n+1) + \psi (k+1) \right] , \end{split} \]
where we have used the limit
\[ \lim_{z\to -n} \,\frac{\psi (z)}{\Gamma (z)} = (-1)^{n-1} n! \, . \]
We can see from the above expression for Yn(x) that it is indeed linearly independent of Jn(x), so that we have two linearly independent solutions of the Bessel equation for integer order n. Also, unlike Jn(x), the Weber function is singular at x = 0.

Using the identity \( \psi (n) = H_{n-1} - \gamma , \) we have

\begin{align*} Y_0 (x) &= \frac{2}{\pi} \left[ \gamma + \ln \left( \frac{x}{2} \right) \right] J_0 (x) - \frac{2}{\pi} \sum_{k\ge 0} \frac{(-1)^k}{k!\, k!}\left( \frac{x}{2} \right)^{2k} H_k , \\ Y_n (x) &= \frac{2}{\pi} \left[ \gamma + \ln \left( \frac{x}{2} \right) \right] J_n (x) - \frac{1}{\pi} \sum_{k= 0}^{n-1} \frac{(n-k-1)!}{k!}\left( \frac{x}{2} \right)^{2k-n} - \frac{1}{\pi} \sum_{k\ge 0} \frac{(-1)^k }{k!\, (k+n)!}\left( \frac{x}{2} \right)^{2k +n} \left[ H_k + H_{k+n} \right] , \end{align*}
where γ ≈ 0.5772156649… is the Euler constant (also called the Euler-Mascheroni constant in honor of Lorenzo Mascheroni (1750--1800)), which is implemented in the Wolfram Language as EulerGamma, and Hn is the n-th harmonic number:
\[ H_n = 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} = \sum_{k=1}^n \frac{1}{k} . \]
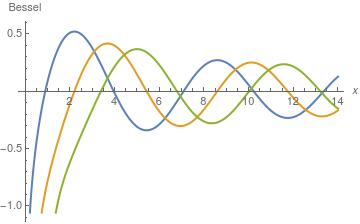
All Weber functions are unbounded at the origin, as it is seen from the plot.
Plot[{BesselY[0, x], BesselY[1, x], BesselY[2, x]}, {x, 0.01, 14}, AxesLabel -> {x, Bessel}, PlotStyle -> {Thick}, PlotLegends -> "Expressions"]
Graphs of Weber functions.
The Wronskian is
\[ W \left[ J_{\nu} (x), Y_{\nu} (x) \right] = J_{\nu +1} (x)\,Y_{\nu} (x) - J_{\nu} (x)\,Y_{\nu +1} (x) = \frac{2}{\pi\,x} . \]
Also
\[ J'_{\nu} (x)\,Y_{\nu} (x) - Y'_{\nu} (x) \,J_{\nu} (x) = - \frac{2}{\pi x} . \]

Integral Representations

Bessel functions of the second kind also have integral representations. We have
\begin{align*} Y_0 (x) &= - \frac{2}{\pi} \int_0^{\infty} \cos \left( x\,\cosh t \right) {\text d} t , \\ Y_n (x) &= \frac{1}{\pi} \int_0^{\pi} \sin \left( x\,\sin t - nt \right) {\text d} t - \frac{1}{\pi} \int_0^{\infty} \left[ e^{nt} +(-1)^n e^{-nt} \right] e^{-x\,\sinh t} {\text d} t . \end{align*}

 

  1. Bowman, Frank Introduction to Bessel Functions (Dover: New York, 1958). ISBN 0-486-60462-4.
  2. Dutka, J., On the early history of Bessel functions, Archive for History of Exact Sciences, volume 49, pages 105–134 (1995). https://doi.org/10.1007/BF00376544
  6. Watson, G.N., A Treatise on the Theory of Bessel Functions, Cambridge University Press; 2nd edition (August 1, 1995). ISBN-13 ‏ : ‎ 978-0521483919

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions