Preface

This section gives an introduction to the most important feature of nonlinear ordinary differential equations: critical or equilibrium points and their stabilities. These points are analyzed without actual solving the differential equation. Stability theory deals with the effect of disturbances on time-processes in real systems. It is also important to know how solutions behave near equilibrium points, including basin of attraction.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part III of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

Stability

We turn our attention to a very important part of the qualitative analysis of differential equations---stability, which can be considered as the study of the effects caused by disturbances. The stability problems originated from mechanics and engineering where possible perturbations should be taken into account. The requirement of keeping some parameters (as the frequency and the voltage) constant under acting disturbances clearly leads to a stability problem. Thus, equilibrium solutions that correspond to configurations in which the physical system does not move, can only be observed in everyday situations when they are stable. An unstable equilibrium can be discovered within a short period of time because slight perturbations in the system or its physical surroundings will immediately dislodge the system far away from equilibrium. It is hard to catch up details for a moving car (unstable), but one can easily observe a parking car (which is in a stable position).

A physical system in perfect balance may be very difficult to achieve (a pencil standing on its point is unstable) or easy to maintain (oscillating pendulum near its downward position). If initial conditions are nudged a little bit, but the resulting solution of the differential equation undergoes a substantial movement away from the equilibrium, we describe this situation as unstable. Without some basic theoretical understanding of the nature of solutions, equilibrium points, and stability properties, one would not be able to understand when numerical solutions (even those provided by standard packages) are to be trusted. Moreover, when testing a numerical scheme, it helps to have already assembled a repertoire of nonlinear problems in which one already knows one or more explicit analytic solutions. Further tests and theoretical results can be based on first integrals (also known as conservation laws) or, more generally, Lyapunov functions, periodic solutions, and chaotic regions. To facilitate understanding, we mostly concentrate our attention on two dimensional case.

A point p is called a critical point or stationary point or equilibrium of the vector differential equation dx/dt = f(x, t) at time t0 if for all t ≥ t0,
\[ {\bf f}({\bf p},t) = {\bf 0} \qquad \mbox{or} \qquad \begin{split} f_1 \left( p_1 , p_2 , \ldots , p_n , t \right) = 0, \\ f_2 \left( p_1 , p_2 , \ldots , p_n , t \right) = 0, \\ \cdots \\ f_n \left( p_1 , p_2 , \ldots , p_n , t \right) = 0, \\ \end{split} \]
where p = [ p1, p2, … , pn ]T is the n-column vector (equilibrium).
The solution set of each equation fk(p1, p2, …, pn) = 0,   k = 1, 2, …, n, is referred to as the k-th nullcline.
Equilibrium or stationary points are intersections of all k-nullclines. Each k-nullcline (if any) separates solutions into disjoint subsets: in one of them the k-th component of the vector solution always increases, while in the other subsets the k-th component decreases.
A critical point x* of the autonomous system dx/dt = f(x) is called an isolated equilibrium point is there is no other stationary point arbitrary closed to it.

In the following, we will also assume that the equilibrium is an isolated critical point. This means that the point p ∈ ℝn is an isolated stationary point, if there is a positive number r such that the r-neighborhood \( U_r = \| {\bf x} - {\bf b} \| < r \) of b contains no critical points other than b. Here

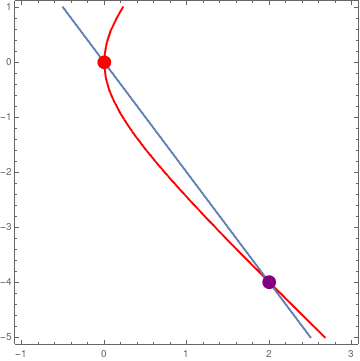
Example 1: The equilibrium points of the nonlinear planar system

\[ \dot{x} = 4\,x - y^2 + 2\,x^2 , \qquad \dot{y} = 2\,x + y , \]
are found by solving the algebraic system
\[ \begin{cases} 4\,x - y^2 + 2\,x^2 &= 0 , \\ 2\,x + y &= 0 . \end{cases} \]
      The x-nullcline is a parabola 4 x = y² - 2 x², and y-nullcline is the straight line y = −2 x. Their intersection consists of two stationary points: the origin (0,0) and (2,−4).
n1 = ContourPlot[4*x - y^2 + 2*x^2 == 0, {x, -1, 3}, {y, -5, 1}, ClippingStyle -> Automatic, ColorFunction -> Hue, ContourStyle -> Thick];
n2 = ContourPlot[2*x + y == 0, {x, -1, 3}, {y, -5, 1}, ClippingStyle -> Automatic, ColorFunction -> Black, ContourStyle -> Thick];
point = Graphics[{PointSize[0.04], Point[{{0, 0}, {2, -4}}, VertexColors -> {Red, Purple}]}];
Show[n1, n2, point]
       Figure 1: Intersections of two nullclines.            Mathematica code

Solve[{2*x + y == 0, 4*x - y^2 + 2*x^2 == 0}, {x, y}]
{{x -> 0, y -> 0}, {x -> 2, y -> -4}}
   ■

Note that if p is an equilibrium of the vector system at t0, then it is also a stationary point for all t ≥ t0. A nonlinear system may have a number of equilibrium states. For autonomous vector equation
\[ \frac{{\text d}{\bf x}}{{\text d}t} = {\bf f} \left( {\bf x} \right) , \]
a point p is an equilibrium at some time t if and only if it is a critical point at all times
\[ {\bf f}\left( {\bf p} \right) = {\bf 0} . \]
The origin x = 0 may or may not be a critical point of a nonlinear system dx/dt = f(x). However, if the system has an equilibrium b that is not the origin, then without any loss of generality, it can be translated to the origin by shifting dependent variables: u = x − b. So we can always assume that the critical point of the system, if it exists, is at the origin. f(b) = 0,

The theory of stability was introduced and further developed by the celebrated Russian mathematician Alexandr Lyapunov (also Liapunov) in 1892. His monograph, entitled: The General Problem of the Stability of Motion, includes so many fruitful ideas and results of primary significance that the whole theory of stability can be divided into two periods, viz. Pre-Lyapunov period and Post-Lyapunov periods.

First of all Lyapunov provided a rigorous definition of motion stability. The absence of such a definition had often caused misunderstandings since otherwise a motion which is stable in one sense can be unstable in another. Then he suggested two main methods for analyzing the stability problems of motions. Of these, the second method, also called The Direct Lyapunov Method is widely popular due to its simplicity and efficiency

Let f be a map f : ℝn → ℝn. Consider a general autonomous (also known as time invariant) vector equation
\begin{equation} \label{EqStability.1} \frac{{\text d} {\bf x}}{{\text d}t} = {\bf f}({\bf x} ) , \qquad {\bf x} \in \mathbb{R}^n . \end{equation}
Let p∈ℝn be a critical point (or stationary point), that is f(p) = 0. This constant function x(t) = p is also called the equilibrium solution of Eq.\eqref{EqStability.1} because it satisfies the vector equation \( \dot{\bf x} = {\bf f}({\bf x}) . \) Any solution y(t) is said to be stable (or Lyapunov stable) if, given ε > 0, there exists a δ = δ(ε) > 0 such that, for any other solution, u(t), of Eq.\eqref{EqStability.1} satisfying ∥y(t0) - u(t0)∥ < δ (where \( \| {\bf x} \| = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \) is a norm in ℝn), then ∥y(t) - u(t)∥ < ε for t > t0, t0∈ℝ. A solution which is not stable is said to be unstable.
An equilibrium solution is stable if whenever the initial state is near that point, but not at the equilibrium point, the state remains near it, as time increases.
Theorem 1: If y(t) is a solution of the autonomous vector differential equation \( {\text d}{\bf x}/{\text d}t = {\bf f}\left( {\bf x} \right) \) in the interval (𝑎, b), then for any constant c the function u(t) = y(t+c) is also a solution of Eq.\eqref{EqStability.1} in the interval (𝑎−c, b−c).
Obviously, the property above does not hold for nonautonomous differential systems.

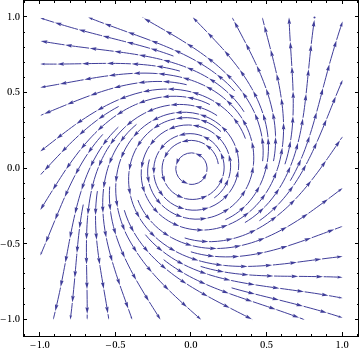
Example 2: Consider the nonlinear system of differential equations \[ \dot{x} = -y + x \left( x^2 + y^2 \right) , \qquad \dot{y} = x + y \left( x^2 + y^2 \right) . \]

      Upon plotting the phase portrait, we see that the origin is a stable critical point.
sp = StreamPlot[{-y + x*(x^2 + y^2), x + y*(x^2 + y^2)}, {x, -1, 1}, {y, -1, 1}, PerformanceGoal -> "Quality", StreamPoints -> 35, PlotTheme -> "Classic"]
       Figure 1: Phase portrait.            Mathematica code

   ■

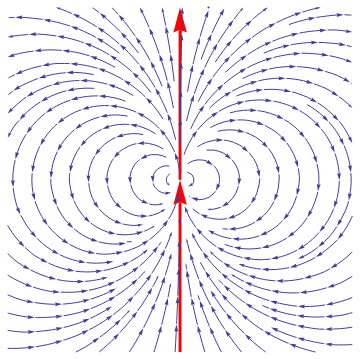
Example: Consider the nonlinear autonomous system of equations

\[ \dot{x} = 2xy , \qquad \dot{y} = y^2 - x^2 . \]
Upon plotting its phase portrait, we observe two families of circles whose midpoints lie on the x-axis and which are tangent to the y-axis at the origin.
     
sp=StreamPlot[{2*x*y, y^2 - x^2}, {x, -1, 1}, {y, -1, 1}, PerformanceGoal -> "Quality", PlotTheme -> "Classic"];
ar = Graphics[{Red, Thickness[0.008], Arrowheads[0.07], Arrow[{{0, -1}, {0, 0}}]}]; line = Graphics[{Red, Thickness[0.008], Arrowheads[0.07], Arrow[{{0, 0}, {0, 1}}]}];
Show[line, ar, sp]
Introducing polar coordinates
\[ x= t\,\cos\theta , \qquad y = r\,\sin\theta , \]
we obtain
\[ \dot{r} = r^2 \sin\theta , \qquad \dot{\theta} = -r\,\cos\theta . \]
We derive the separable equation
\[ \frac{{\text d}r}{{\text d}\theta} = \frac{\dot{r}}{\dot{\theta}} = -r\,\tan\theta \qquad \left( \theta \ne \frac{\pi}{2} , \quad \theta \ne \frac{3\pi}{2} \right) . \]
       Figure 1: Phase portrait.            Mathematica code

The solution of the latter becomes
\[ r = \rho (t) = r_0 \left\vert \cos\theta \right\vert , \qquad \theta \ne \frac{\pi}{2} , \quad \theta \ne \frac{3\pi}{2} , \]
and
\[ \theta = \frac{\pi}{2} , \quad \theta = \frac{3\pi}{2} . \]
The two halves of the y-axis are also trajectories; they decompose the plane into two elliptic sectors, so they form the separatrix. Along the y-axis we have
\[ \dot{r} = \pm t^2 \qquad \Longrightarrow \qquad \rho (t) = \left( \frac{1}{r_0} -t \right)^{-1} \quad \mbox{ or } \quad \rho (t) = \left( \frac{1}{r_0} +t \right)^{-1} . \]
So one of the solutions blows up. The remaining motions tend toward the origin. Arbitrarily close to the origin there exist starting points such that the phase curve passing through them moves further than an arbitrarily pre-assigned distance R away from the origin. These starting points lie between the circles with radius R centered at (R/2, 0) and (−R/2, 0). The larger R becomes, the narrower is the intersection of the two circular discs.    ■

The constant solution x(t) = p of the autonomous vector differential equation \( \dot{\bf x} = {\bf f}({\bf x}) \) is asymptotically stable if it is stable and, moreover, there exists δ > 0 such that if the initial position x0 is closed to the critical point p, so \( \| {\bf x}_0 - {\bf p} \| < \delta , \) then \( \lim_{t\to +\infty} {\bf x}\left( t; t_0 , {\bf x}_0 \right) = {\bf p} , \) where x(t; t0, x0) is the solution to the initial value problem
\begin{equation} \label{EqStability.2} \dot{\bf x} = {\bf f}({\bf x}) , \qquad {\bf x}\left( t_0 \right) = {\bf x}_0 . \end{equation}

Example:    ■

An important generalization of the previous definition is uniform asymptotic stability when both of the initial moment t0 and of the initial position x0 of the the perturbed motion do not affect the long-term behavior of the solution.

The equilibrium solution x(t) = p of the autonomous vector differential equation \( \dot{\bf x} = {\bf f}({\bf x}) \) is uniformly asymptotically stable if there exist a positive number δ0 and functions δ(·), T(·) such that \( \| {\bf x}_0 - {\bf p} \| < \delta (\varepsilon ) \) implies \( \| {\bf x} \left( t; t_0 ,{\bf x}_0 \right) - {\bf p} \| < \varepsilon \) , for all t ≥ t0 and if \( \| {\bf x}_0 - {\bf p} \| < \delta_0 , \) then \( \| {\bf x}\left( t; t_0 , {\bf x}_0 \right) - {\bf p} \| < \varepsilon \) for all t ≥ t0 + T(ε).
Asymptotic stability does not imply anything about how long it takes to converge to a prescribed critical point. On the other hand, in case of constant coefficient autonomous vector differential equation, asymptotic stability implies exponential convergence to the stationary point because we know the structure of the exponential matrix \( e^{{\bf A}t} . \)

There is a domain of attraction such that whenever the initial condition belongs to this domain the solution approaches the equilibrium state at large times.
Let p be a critical point of the system of autonomous equations dx/dt = f(x). If p is an attractor, then the set of points in the space of system variables such that initial conditions chosen in this set dynamically evolve to a particular attractor is called the basin of attraction or region of asymptotic stability.
For an attractor, its basin of attraction is the set of initial conditions leading to long-time behavior that approaches that attractor. Thus the qualitative behavior of the long-time motion of a given system can be fundamentally different depending on which basin of attraction the initial condition lies in (e.g., attractors can correspond to periodic, quasiperiodic or chaotic behaviors of different types).

There are known other definitions of stability (for instance, in Poincaré sense); however, the definitions above (in Lyapunov sense) are mostly used. Before the end of the nineteen century, most of research and applications of differential equations was centered around the analytic expression of solutions of differential equations. Upon the influence of the famous French mathematician Henri Poincaré (1854--1912), the topic of differential equations shifted to the study of the global properties of the solutions without solving the differential equations themselves. The important contributions of Poincaré came at the eve of twentieth century slightly later the Lyapunov discovery. Stability applications have seeped into industry such as in engineering applications, where the common practice is to run a process in “steady state”. For the system that the engineer is interested in, it is frequently of much greater importance to know that the system is approaching a stable equilibrium and will remain there for long time periods, than to have an exact computation of short term transient behavior. Computers make it possible to find approximately the solutions of differential equations on a finite interval of time, but they do not answer the qualitative aspects of the global behavior of phase curves.

A fundamental problem in the theory of differential equations is to study the motion of the system u sing the vector field that induces the differential equations. Qualitative analysis involves questions of the type: Do the solutions go to infinity, or do they remain bounded within a certain region? What conditions must a vector field satisfy in order for the solutions to remain within a given region? Do nearby solutions act similarly to a particular solution of interest? These are questions of qualitative type, in contrast with analytic methods that tend to search for a formula to express each solution of a differential equation. Some authors separate asymptotic stability property when t → ∞ from stability and consider asymptotic stability without requirement for critical point to be stable.

If an unstable equilibrium solution x* of the autonomous vector equation \eqref{EqPlanar.2} is approached by other solutions x(t) = ψ(t) so that
\[ \lim_{t\to \infty} \left\| {\bf x}^{\ast} - \psi (t) \right\| = 0, \]
then x* is called quasi-asymptotically stable.
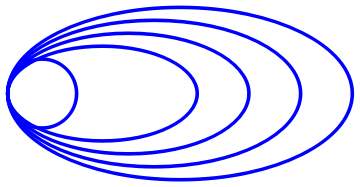
      x* A typical quas-asymptotically stable critical point may have the following phase portrait.
c1 = Graphics[{Blue, Thickness[0.01], Circle[{0, 0}, 0.4]}];
c2 = Graphics[{Blue, Thickness[0.01], Circle[{1.6, 0}, {2, 1}]};
c3 = Graphics[{Blue, Thickness[0.01], Circle[{1.3, 0}, {1.7, 0.85}]}];
c4 = Graphics[{Blue, Thickness[0.01], Circle[{1.0, 0}, {1.4, 0.7}]}];
c5 = Graphics[{Blue, Thickness[0.01], Circle[{0.7, 0}, {1.1, 0.55}]}];
Show[c1, c2, c3, c4, c5]
       Quas-asymptotically stable critical point            Mathematica code

An equilibrium x* is unstable if there exists a positive number ε such that for any δ ≤ ε such that there is at least one solution x = φ(t) that starts within δ-neighborhood of the critical point and be at distance more that ε from the equilibrium solution.

 

The following (pathological) examples demonstrate that an equilibrium solution can be unstable, but asymptotically stable. This means that there exists a positive number ε such that the magnitude of every nearby solution exceeds it, but eventually all solutions approach the critical point as t → ∞.

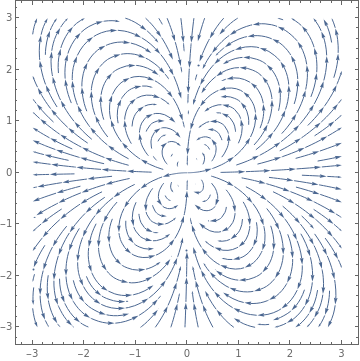
Example: Consider the following system \eqref{EqPlanar.1} due to Thomas Brown (Rassias, J.M., Counter-Examples in Differential Equations, page 95 )

\[ \frac{{\text d}x}{{\text d}t} = \begin{cases} 2xy, & \ \mbox{ in } \Omega_1 \cup \Omega_2 \cup \Omega_3 , \\ \frac{2xy}{3 - 4\,|x|}, & \ \mbox{ in } \Omega_4 ; \end{cases} \qquad \frac{{\text d}y}{{\text d}t} = \begin{cases} y^2 - x^2 , & \ \mbox{ in } \Omega_1 \cup \Omega_2 \\ 4\,|x| - y^2 - 3 x^2 , & \ \mbox{ in } \Omega_3 , \\ \frac{4\,|x| - y^2 - 3 x^2}{3 - 4/|x|} , & \ \mbox{ in } \Omega_4 ; \end{cases} \]
where
\begin{align*} \Omega_1 : &\mbox{the lower half-plane } \ y \le 0; \\ \Omega_2 : &\mbox{the locus } \ x^2 + y^2 \le 2|x|, \mbox{ consisting of the discs } \ \left( x \pm 1 \right)^2 + y^2 \le 1; \\ \Omega_3 : &\mbox{the half-strip } \ |x| \le 2, \ y > 0 , \ \mbox{ extended to } \ \Omega_2 ; \\ \Omega_4 : &\mbox{the locus } \ |x| > 2, \ y> 2 . \end{align*}
This system of equations is unstable, but
\[ \lim_{t\to\infty} \left\vert x(t) \right\vert =0 , \qquad \lim_{t\to\infty} \left\vert y(t) \right\vert =0 , \]
for all orbits.
     
circle1 = Graphics[{Thick, Blue, Circle[{0.5, 0.0}, 0.5]}];
circle2 = Graphics[{Thick, Blue, Circle[{1.0, 0.0}, 1.0]}];
arrow1 = Graphics[{Arrowheads[0.04], Blue, Arrow[{{0.98, 0.15}, {1.0, 0}}]}];
arrow2 = Graphics[{Arrowheads[0.045], Blue, Arrow[{{1.98, 0.15}, {2.0, 0}}]}];
circle3 = Graphics[{Thick, Blue, Circle[{1.5, 0.0}, 1.5]}];
arrow3 = Graphics[{Arrowheads[0.045], Blue, Arrow[{{2.98, 0.15}, {3.0, 0}}]}];
c1a = Graphics[{Thick, Blue, Circle[{-0.5, 0.0}, 0.5]}];
a1a = Graphics[{Arrowheads[0.04], Blue, Arrow[{{-0.98, 0.15}, {-1.0, 0}}]}];
c2a = Graphics[{Thick, Blue, Circle[{-1.0, 0.0}, 1.0]}];
a2a = Graphics[{Arrowheads[0.045], Blue, Arrow[{{-1.98, 0.15}, {-2.0, 0}}]}];
c3a = Graphics[{Thick, Blue, Circle[{-1.5, 0.0}, 1.5]}];
a3a = Graphics[{Arrowheads[0.045], Blue, Arrow[{{-2.98, 0.15}, {-3.0, 0}}]}];
c4a = Graphics[{Thick, Blue, Circle[{-2.2, 0.0}, 2.2, {0, -4.5}]}];
c4 = Graphics[{Thick, Blue, Circle[{2.2, 0.0}, 2.2, {-Pi, 1.6}]}];
a4 = Graphics[{Arrowheads[0.05], Blue, Arrow[{{0.32, -1.19}, {0.24, -1.1}}]}];
a4a = Graphics[{Arrowheads[0.05], Blue, Arrow[{{-0.32, -1.19}, {-0.24, -1.1}}]}];
exp = Plot[2.08 + Exp[-x], {x, 0.4, 2.1}, PlotStyle -> {Thick, Blue}];
expa = Plot[2.08 + Exp[x], {x, -2.6, -0.4}, PlotStyle -> {Thick, Blue}];
xa = Graphics[{Arrowheads[0.05], Black, Arrow[{{-4.0, 0}, {5.0, 0}}]}];
xt = Graphics[ Text[StyleForm["x", FontSize -> 18, FontColor -> Black], {4.8, 0.4}]];
ya = Graphics[{Arrowheads[0.05], Black, Arrow[{{0.0, -2.0}, {0.0, 3.7}}]}];
yt = Graphics[ Text[StyleForm["y", FontSize -> 18, FontColor -> Black], {0.4, 3.6}]];
Show[circle1, arrow1, circle2, arrow2, circle3, arrow3, c1a, a1a, c2a, a2a, c3a, a3a, c4, c4a, a4, a4a, exp, expa, ya, yt, xa, xt]
       Some solution trajectories.            Mathematica code

   ■

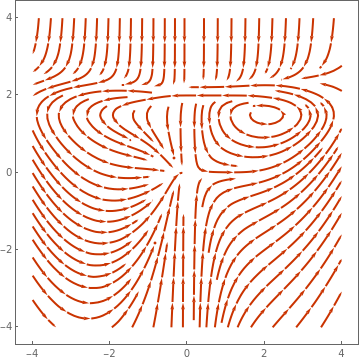
Example: Consider the planar system

\[ \frac{{\text d}x}{{\text d}t} = x-y + \frac{xy - x^3 - y^2 x}{\sqrt{x^2 + y^2}} , \qquad \frac{{\text d}y}{{\text d}t} = x+y - \frac{x^2 + y^3 + x^2 y}{\sqrt{x^2 + y^2}} \]
Upon plotting its phase portrait, we see that the origin is unstable critical point, but (1, 0) is a quasi-stable equilibrium position.
     
StreamPlot[{x - y + (x*y - x^3 - x*y^2)/Sqrt[x^2 + y^2], x + y - (x^2 + y^3 + y*x^2)/Sqrt[x^2 + y^2]}, {x, -2, 2}, {y, -2, 2}, Mesh -> 11, MeshShading -> {Red, None}]
       Figure 2: Quasi-stable critical point (1,0).            Mathematica code

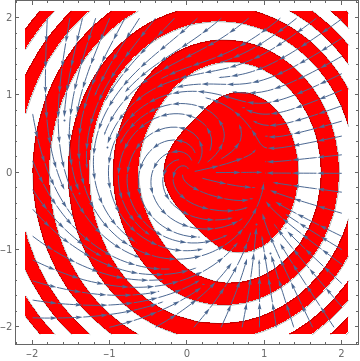
Another unprecedentedly ugly example of quisi-stable system: All solutions nearby 0 goes back to 0, since nearby solutions in the left half plane naturally converge to 0, and nearby solutions in the right half plane first converge to the x-axis, then wind back to the left half plane.

     
StreamPlot[{x^2 + (-(x^2 + 1/16) (y - 1/2)^3) Boole[y >= 1/2], -y + (y - 1)^2 y Boole[y >= 1] - 500 (y - 2)^4 Boole[y >= 2] + (x + 1)^3 Boole[x <= -1] + (x - 1)^3 Boole[x >= 1]}, {x, -4, 4}, {y, -4, 4}, PlotTheme -> "Web"]
       Figure 3: Quasi-stable critical point (1,0).            Mathematica code

   ■

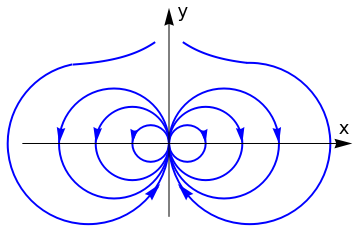
Example: Consider an electric field E given by

\[ {\bf E} = \frac{1}{r^4} \left( 3\cos^2 \theta -1 \right) {\bf r} + \frac{1}{r^4} \,\sin (2\theta )\, \overrightarrow{\theta} . \]
To plot a direction field with Mathematica, we need to convert polar coordinates into rectangular ones because Mathematica provides StreamPlot only for Cartesian coordinates. First, we convert our field
field = 3/(4 r^4) (3 Cos[\[Theta]]^2 - 1) Overscript[r, "^"] + 3/(4 r^4) Sin[2 \[Theta]] Overscript[\[Theta], "^"]
(3 (-1 + 3 Cos[\[Theta]]^2) \!\(\*OverscriptBox[\(r\), \("^"\)]\))/(4 r^4) + (3 \!\(\*OverscriptBox[\(\[Theta]\), \("^"\)]\) Sin[2 \[Theta]])/(4 r^4)
to Cartesian form.
tocartesian = {Overscript[r, "^"] -> x/r Overscript[x, "^"] + y/r Overscript[y, "^"], Overscript[\[Theta], "^"] -> -(y/Sqrt[x^2 + y^2]) Overscript[x, "^"] + x/Sqrt[x^2 + y^2] Overscript[y, "^"], r -> Sqrt[x^2 + y^2], \[Theta] -> ArcTan[x, y]};
and a rule to make this into a list afterwards
cartesianlist = (a_ Overscript[x, "^"] + b_ Overscript[y, "^"]) -> {a, b};
Then we can let Mathematica repeatedly apply (//.) our tocartesian rule to eliminate all occurences of r and then let FullSimplify help us to eliminate the trigonometric functions. At last we use cartesianlist to switch to list form:
cartesianfield = FullSimplify[field //. tocartesian] /. cartesianlist
{(6 x^3 - 9 x y^2)/( 4 (x^2 + y^2)^(7/2)), -((3 y (-4 x^2 + y^2))/(4 (x^2 + y^2)^(7/2)))}
For convenient usage we define our own PolarStreamPlot function
PolarStreamPlot[{rfield_, thetafield_}, opts___] :=
Module[{tocartesian, cartesianlist, field, cartesianfield}, tocartesian = {Overscript[r, "^"] -> x/r Overscript[x, "^"] + y/r Overscript[y, "^"], Overscript[\[Theta], "^"] -> -(y/Sqrt[x^2 + y^2]) Overscript[x, "^"] + x/Sqrt[x^2 + y^2] Overscript[y, "^"], r -> Sqrt[x^2 + y^2], \[Theta] -> ArcTan[x, y]};
cartesianlist = (a_ Overscript[x, "^"] + b_ Overscript[y, "^"]) -> {a, b};
field = rfield Overscript[r, "^"] + thetafield Overscript[\[Theta], "^"];
cartesianfield = FullSimplify[field //. tocartesian] /. cartesianlist;
StreamPlot[cartesianfield, opts]]
      Now we can feed it our original r-θ field definition directly
PolarStreamPlot[{3/(4 r^4) (3 Cos[\[Theta]]^2 - 1), 3/(4 r^4) Sin[2 \[Theta]]}, {x, -3, 3}, {y, -3, 3}, PlotTheme -> "Detailed"]
       Figure 4: Quasi-stable electric field.            Mathematica code
   ■
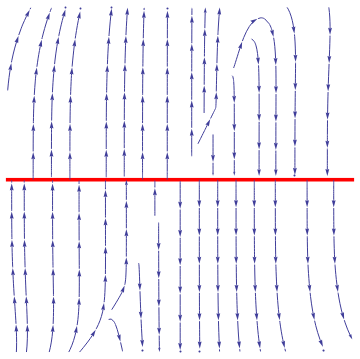
Example 4: W.Hahn, 1967. A system whose all solutions are approaching the equilibrium, x = 0, without this equilibrium being asymptotically stable
\[ \dot{x} = \frac{x^2 \left( y-x \right) y^5}{\left( x^2 + y^2 \right) \left( 1 + \left( x^2 + y^2 \right)^2 \right)} , \qquad \dot{y} = \frac{y^2 \left( y - 2x \right)}{\left( x^2 + y^2 \right) \left( 1 + \left( x^2 + y^2 \right)^2 \right)} . \]
      We plot the phase portrait for the given system of nonlinear differential equations
f1[x_, y_] = x^2 *(y - x)*y^5/(x^2 + y^2)/(1 + (x^2 + y^2)^2);
f2[x_, y_] = y^2 *(y - 2*x)/(x^2 + y^2)/(1 + (x^2 + y^2)^2);
sp = StreamPlot[{f1[x, y], f2[x, y]}, {x, -1, 1}, {y, -1, 1}, PerformanceGoal -> "Quality", StreamPoints -> 35, PlotTheme -> "Classic"];
line = Graphics[{Red, Thickness[0.01], Line[{{-1, 0}, {1, 0}}]}];
Show[line, sp]
       Figure 1: Phase portrait.            Mathematica code

   ■
We will mostly apply stability or instability property to isolated stationary points for autonomous equations.
A solution y(t) of Eq.\eqref{EqStability.1} is said to be asymptotically stable if it is Lyapunov stable and for any other solution u(t) of Eq.\eqref{EqStability.1}, there exists a constant b > 0 such that, if ∥y(t0) - u(t0)∥ < b, then \( \lim_{t\to +\infty} \| {\bf y}(t) - {\bf u}(t) \| = 0. \)
If every solution of the autonomous system \eqref{EqStability.1} approaches some solution y(t), not necessarily critical point, as t → +∞, then it is called globally asymptotically stable.
Both definitions imply that we have information on the infinite time existence of solutions. This is obvious for equilibrium solutions, but is not necessarily so for nearby solutions. Note that these definitions are for autonomous systems because for nonautonomous systems parameters δ and b depend explicitly on t0.
Theorem 2: All solutions of the linear differential system \( \dot{\bf y} = {\bf A}(t)\,{\bf y} \) are stable if and only if they are bounded.
Corollary 1: If the real parts of the multiple eigenvalues of the matrix A are negative, and the real parts of the simple eigenvalues of the matrix A are nonpositive, then all solutions of the linear constant coefficient vector differential equation \( \dot{\bf y} = {\bf A}\,{\bf y} \) are stable.
Corollary 2: If the real parts of the eigenvalues of the matrix A are negative, then all solutions of the linear constant coefficient vector differential equation \( \dot{\bf y} = {\bf A}\,{\bf y} \) are asymptotically stable.

The stability of equilibrium solutions of constant coefficient linear systems of differential equations depends completely on the roots of the characteristic polynomial det(λI − A) = 0. The following theorem, credited to the German mathematician Adolf Hurwitz (1859–1919).

Theorem Hurwitz: A necessary and sufficient condition for the negativity of the real parts of all zeros of the polynomial
\[ \lambda^n + a_{n-1} \lambda^{n-1} + \cdots + a_1 \lambda + a_0 \]
with real coefficients is the positivity of all the leading principal minors of the n × n Hurwitz matrix
\[ \begin{pmatrix} a_{n-1} & 1 & 0 & 0 & 0 & \cdots & 0 \\ a_{n-3} & a_{n-2} & a_{n-1} & 1 & 0 & \cdots & 0 \\ a_{n-5} & a_{n-4} & a_{n-3} & a_{n-2} & a_{n-1} & \cdots & 0 \\ \vdots& \vdots & \vdots & \vdots& \vdots & \ddots & \vdots \\ 0&0&0&0&0 & \cdots & a_0 \end{pmatrix} , \]
that is,
\[ a_{n-1} > 0, \quad \begin{vmatrix} a_{n-1} & 1 \\ a_{n-3} & a_{n-2} \end{vmatrix} > 0 , \quad \begin{vmatrix} a_{n-1}& 1 & 0 \\ a_{n-3}& a_{n-2} & a_{n-1} \\ a_{n-5} & a_{n-4} & a_{n-3} \end{vmatrix} > 0 , \ldots . \]
Let x(t) = p be a critical point of the autonomous vector differential equation \( \dot{\bf y} = {\bf f}\left( {\bf y} \right) , \) x∈ℝn and f = [f1, f2, … , fn]T be a holomorphic vector function in a neighborhood of the isolated critical point p. Then the critical point is called a hyperbolic if none of the eigenvalues of the Jacobian matrix
\begin{equation} \label{EqStability.3} {\bf J} ({\bf p}) = \texttt{D}{\bf f}({\bf p}) = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \cdots & \frac{\partial f_n}{\partial x_n} \end{bmatrix}_{{\bf x} = {\bf p}} \end{equation}
have zero real part.

Planar Systems

The concepts of asymptotic stability, stability, and instability can be easily visualized by considering two-dimensional models. Let φ(t) = [x(t), y(t)] be the trajectory and x∗ = (x∗, (y∗) be an isolated critical point to the autonomous system. We say that a point P((x, y) approaches he critical point x∗ if \( \lim_{t\to\infty} x(t) = x^{\ast} \) and \( \lim_{t\to\infty} y(t) = y^{\ast} \) ✴

We consider systems of first order ordinary differential equations in normal form on the plane

\begin{equation} \label{EqPlanar.1} \begin{cases} \dot{x} = f (x , y) , \\ \dot{y} = g (x , y) , \end{cases} \end{equation}
where we use notation x and y for dependent variables. As usual, the overdot denotes the derivative with respect to time variable t. Of course, the above system can be written in compact vector form
\begin{equation} \label{EqPlanar.2} \frac{{\text d} {\bf x}}{{\text d}t} = {\bf f}({\bf x} ) , \end{equation}
where
\[ {\bf x} (t) = \begin{bmatrix} x (t) \\ y (t) \end{bmatrix} , \qquad {\bf f} (x , y) = \begin{bmatrix} f (x , y) \\ g (x , y) \end{bmatrix} \]
are 2-column vectors. In engineering and physics, it is a custom to denote a derivative with respect to time variable t by dot: \( \dot{\bf x} = {\text d}{\bf x} / {\text d} t. \)

Example 5:    ■

 

  1. Alligood, K.T., Sauer, T.D., and Yorke, J.A., Chaos. An Introduction to Dynamical Systems, 1996, Springer-Verlag, New York, QA614.8.A44 1996
  2. Cesari, L., Asymptotic Behavior and Stability Problems in Ordinary Differential Equations, Springer-Verlag, Berlin, Heidelberg, 2014. ISBN-13 : 978-3662015308
  3. Hahn, W. Stability of Motion, Springer-Verlag, Berlin, Heidelberg, 1967.

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions