Preface

This section provides numerous examples of modeling in mechanical problems.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part I of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

Mechanical Problems

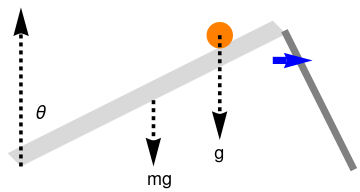
Example 1: The following example is inspired by a phenomenon presented in Sutton's classical book (Demonstration Experiments in Physics, McGraw-Hill, New York, 1938) for demonstration that different points at a rigid rod pivoted at one end have distinct falling accelerations that can exceed the corresponding acceleration of the center of mass. Its analysis leads to determination of the center of percussion or center of oscillation of a rigid rod/stick (with respect to a particular axis of rotation)

If we neglect friction, all freely falling point objects will fall at the acceleration of gravity, commonly called g. A ball is placed on one end of a uniform rod/stick , which is pivoted at the other end and makes initially an angle of about π/6 radians with the horizontal surface. The support of the elevated end of the stick is suddenly dropped, together with the ball. The falling end of the stick accelerates at a greater rate than the free-falling ball, proving that its acceleration is greater than g, the acceleration of gravity.

      We plot the falling stick with a ball:
rod = Graphics[{LightGray, Polygon[{{0, 0}, {-0.1, 0.1}, {1.9, 1.1}, {2.0, 1.0}}]}];
support = Graphics[{Gray, Thickness[0.02], Line[{{2.5, 0}, {2.0, 1.0}}]}];
ball = Graphics[{Orange, Disk[{1.5, 0.99}, 0.1]}];
ar = Graphics[{Blue, Thickness[0.02], Arrowheads[0.08], Arrow[{{1.9, 0.8}, {2.2, 0.8}}]}];
ar1 = Graphics[{Black, Dashed, Thickness[0.01], Arrowheads[0.08], Arrow[{{1, 0.5}, {1, 0}}]}];
ar2 = Graphics[{Black, Dashed, Thickness[0.01], Arrowheads[0.08], Arrow[{{0, 0}, {0, 1.2}}]}];
ar3 = Graphics[{Black, Dashed, Thickness[0.01], Arrowheads[0.08], Arrow[{{1.5, 0.99}, {1.5, 0.2}}]}];
t1 = Graphics[{Black, Text[Style["g", 18], {1.5, 0.1}]}];
t2 = Graphics[{Black, Text[Style["\[Theta]", 18], {0.15, 0.4}]}];
t3 = Graphics[{Black, Text[Style["mg", 18], {1.05, -0.1}]}];
Show[rod, support, ball, ar, ar1, ar2, ar3, t1, t2, t3]
       Falling stick with a ball.            Mathematica code

Let θ = θ(t) be the angular displacement of the rod from the vertical axis at time t, with θ0 = θ(0) defining the initial elevation of stick end. Suppose that the rod has length ℓ and mass m, with center of gravity at a distance of λℓ, from the hinge. The uniform rod has the moment of inertia around the axis at the hinge to be I0 = βmℓ². For the case of a thin uniform rod, λ = ½ and β = ⅓. Since any point object falls with a constant acceleration g ≈ 9.81, we can assume that the ball is of unit mass.

The equation for the rod along (without the ball) can be obtained by using Newton's second law for rotation around a fixed hinged point (which can be chosen as the origin) to give

\[ \beta m \ell^2 \ddot{\theta} = \lambda \ell mg\,\sin\theta \qquad \Longleftrightarrow \qquad \ddot{\theta} = \omega^2 \sin\theta , \tag{1.1} \]
where
\[ \omega^2 = \frac{\lambda g}{\beta\ell} \quad \left[ = \frac{3g}{2\ell} \quad\mbox{in uniform case} \right] \tag{1.2} \]
Since this is a standard pendulum equation, we can integrate under the initial conditions
\[ \theta (0) = \theta_0 , \quad \dot{\theta}(0) = 0 . \]
This gives us the velocity:
\[ \frac{1}{2}\,\left( \dot{\theta} \right)^2 = \omega^2 \int_{\theta_0}^{\theta} \sin\psi\,{\text d}\psi \qquad \Longrightarrow \qquad \dot{\theta} (t) = \omega\sqrt{\lambda} \left[ \cos\theta_0 - \cos \theta \right]^{1/2} \tag{1.3} \]
The time required for rotation from θ0 to π/2 can now be found by integrating \( {\text d}t/{\text d}\theta = \left( \dot{\theta} \right)^{-1} \) from Eq.(3.3) to get
\[ T = \int_{\theta_0}^{\pi /2} \left( \dot{\theta} \right)^{-1} {\text d}\theta . \tag{1.4} \]
You can compare its value with time needed for the ball to reach the growund:
\[ T_0 = \left[ \frac{2\alpha \ell}{g}\,\cos\theta_0 \right]^{1/2} \tag{1.5} \]
that follows from the equation \( \alpha \ell \cos\theta_0 = \frac{1}{2}\, g\,T_0^2 . \)

The critical position of the ball is determined by α = α* when the acceleration of the point of its contact is equal to g. Since the acceleration of any point located at αℓ position is

\[ a = \alpha\ell\,\ddot{\theta} = \frac{\alpha\ell}{\beta}\,g\sin\theta . \]
Equating its value to gsinθ, we obtain the critical position
\[ \alpha^{\ast} = \beta / \lambda \quad \left[ = \frac{2}{3} \quad\mbox{in the uniform case} \right] . \tag{1.6} \]

However, the value (3.6) does not guarantee that the rod reaches the ground before the ball does. To calculate T from Eq.(1.4), we transfer the integral by substitution

  1. Adams, J.L., Acceleration greater than "g", The Physics Teacher, 1982, Issue 2, pp. 100--101; https://doi.org/10.1119/1.2340956
  2. Bacon, M.E., Harpst, M.R., and Nakazawa, R., Falling sticks and falling balls, The Physics Teacher, 2002, 40, 333–335 (Sept. 2002)
  3. Haber-Schaim, U., On qualitative problems, The Physics Teacher, 1992, 30, Issue 5, p. 260; https://doi.org/10.1119/1.2343533
  4. Härtel, H., The falling stick with 𝑎 > g, The Physics Teacher, 2000, 38, January, pp. 54--55. https://doi.org/10.1119/1.880430
  5. Hilton, W.A., Free fall paradox, The Physics Teacher, 1965, 3, Issue 7, pp. 323--324, https://doi.org/10.1119/1.2349174
  6. Shash, S., Shore, J.A., and Spekkens, K., The falling rod race, The Physics Teacher, 2020, 58, November, pp. 596--598; https://doi.org/10.1119/10.0002387
  7. Theron, W., The "faster than gravity" demonstration revisited, American Journal of Physics, 1988, 56, Issue 8, pp. 736--739. https://doi.org/10.1119/1.15513
  8. Varieschi, G, and Kamiya, K., Toy models for the falling chimney, American Journal of Physics, 2003, 71, No, 9, pp. 1025--1031. https://doi.org/10.1119/1.1576403
  9. Young, W.M., Faster than gravity!, American Journal of Physics, 1984, 52, No. 12, pp. 1142--1143. https://doi.org/10.1119/1.13745
   ■

 

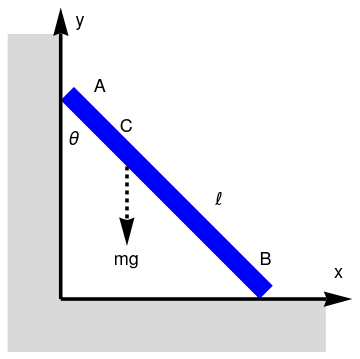
The sliding ladder paradox

In this section, we consider a classical problem of sliding under gravity a rigid ladder that is supported at a vertical wall with one end while touching a horizontal floor with another end. There are many versions of this problem either taking into account friction at one of the ends or considering nonuniform ladder. In 1985, Freeman and Palffly-Muhoray noted that motion of the top end of the ladder approaches infinite speed that gave them a reason to call this problem a paradox. Actually, the learning ladder is loosing a contact with the wall at some point and becomes a pendulum pivoting at its floor end.

We sketch the learning ladder with Mathematica:

pol = Graphics[{LightGray, Polygon[{{0, 0}, {0, 2}, {-0.4, 2}, {-0.4, -0.4}, {2, -0.4}, {2, 0}, {0, 0}}]}];
ladder = Graphics[{Blue, Polygon[{{0, 1.5}, {0.1, 1.6}, {1.6, 0.1}, {1.5, 0}}]}];
ar1 = Graphics[{Black, Thickness[0.01], Arrowheads[0.08], Arrow[{{0, 0}, {2.2, 0}}]}];
ar2 = Graphics[{Black, Thickness[0.01], Arrowheads[0.08], Arrow[{{0, 0}, {0, 2.2}}]}];
ar3 = Graphics[{Black, Dashed, Thickness[0.01], Arrowheads[0.08], Arrow[{{0.5, 1}, {0.5, 0.4}}]}];
tl = Graphics[{Black, Text[Style["\[ScriptL]", 18, FontFamily -> "Mathematica1"], {1.2, 0.75}]}];
tx = Graphics[{Black, Text[Style["x", 18], {2.1, 0.2}]}];
ty = Graphics[{Black, Text[Style["y", 18], {0.15, 2.1}]}];
tA = Graphics[{Black, Text[Style["A", 18], {0.3, 1.6}]}];
tB = Graphics[{Black, Text[Style["B", 18], {1.55, 0.3}]}];
tC = Graphics[{Black, Text[Style["C", 18], {0.5, 1.3}]}];
t3 = Graphics[{Black, Text[Style["mg", 18], {0.5, 0.3}]}];
t4 = Graphics[{Black, Text[Style["\[Theta]", 18], {0.1, 1.2}]}];
Show[pol, ladder, ar1, ar2, ar3, t3, t4, tx, ty, tl, tA, tB, tC]
Ladder diagram
We assume that the ladder of length ℓ and mass m makes an angle θ(t) with the vertical positive axis (y) in two dimensional xy-space. The center of mass is situated at point C, which in case of a uniform stick is in the center of ladder. The top end of the ladder is denoted by A and it touched the floor at point B.

In 1744, L.Euler introduced the angular momentum (moment of momentum) A of a system of particles with respect to the fixed origin of an inertial frame

\begin{equation} \label{EqMoment.1} {\bf A} = \sum_{\alpha} {\bf x}_{\alpha} \times {\bf p}_{\alpha} = \sum_{\alpha} {\bf x}_{\alpha} \times m_{\alpha} {\bf v}_{\alpha} , \end{equation}
where xα and pα are the vectors of position and momentum of the αth particle of mass mα, respectively. For a corresponding Lagrangian ℒ(x, v), we have
\[ {\bf p}_{\alpha} = \partial{\cal L}/\partial {\bf v}_{\alpha} . \]
The moments of a particle is defined by
\[ {\bf p}_{\alpha} = m_{\alpha} {\bf v}_{\alpha} = m_{\alpha} \frac{\text d}{{\text d}t} \,{\bf x}_{\alpha} = m_{\alpha} \dot{\bf x}_{\alpha} . \]
Then differentiating Eq.\eqref{EqMoment.1}, we get
\[ \frac{\text d}{{\text d}t} \,{\bf A} = \sum_{\alpha} \left( {\bf v}_{\alpha} \times {\bf p}_{\alpha} + {\bf x}_{\alpha} \times \frac{\text d}{{\tyext d}t} \,{\bf p}_{\alpha} \right) . \]
But vα × pα = mαvα × vα = 0; therefore,
\[ \frac{\text d}{{\text d}t} \,{\bf A} = \sum_{\alpha} {\bf x}_{\alpha} \times \frac{\text d}{{\text d}t} \,{\bf p}_{\alpha} \]
Now Newton's second law of motion, applied to the αth particle, is
\[ \frac{\text d}{{\text d}t} \,{\bf p}_{\alpha} = {\bf F}_{\alpha} , \]
where Fα is the resultant of forces acting on the αth particle.

The system of particles is now assumed to be isolated. This implies that Fα is the resultant only of the forces that all the other particles exert on the αth particles. Hence,

\[ {\bf F}_{\alpha} = \sum_{\beta \ne \alpha} {\bf F}_{\alpha\beta} , \]
where Fαβ is the force that the βth particle exerts on the αth particle. Then
\begin{align*} \frac{\text d}{{\text d}t} \,{\bf A} &= \sum_{\alpha} {\bf x}_{\alpha} \times {\bf F}_{\alpha} = \sum_{\alpha} {\bf x}_{\alpha} \times \sum_{\beta \ne \alpha} {\bf F}_{\alpha\beta} \\ \sum_{\alpha} \, \sum_{\beta \ne \alpha} {\bf x}_{\alpha} \times {\bf F}_{\alpha\beta} . \end{align*}
Now for every pair of numbers (α, β) in the summation there is another pair (β, α). The latter equation can be written as
\[ \frac{\text d}{{\text d}t} \,{\bf A} = \sum_{\alpha} \, \sum_{\beta \ne \alpha} \left( {\bf x}_{\alpha} \times {\bf F}_{\alpha\beta} + {\bf x}_{\beta} \times {\bf F}_{\beta\alpha} \right) . \]
Newton's third law of motion, in our notation, is
\[ {\bf F}_{\beta\alpha} = - {\bf F}_{\alpha\beta} , \]
so that finally the rate of change of the angular momentum becomes
\[ \frac{\text d}{{\text d}t} \,{\bf A} = \sum_{\alpha} \, \sum_{\beta \ne \alpha} \left( {\bf x}_{\alpha} - {\bf x}_{\beta} \right) \times {\bf F}_{\alpha\beta} . \]
The expression under summation, (xα - xβ) × Fαβ is the torque produced by a couple: Fαβ at the particle α and Fβα at particle β. This leads to the strong form of Newton's third law: in the interaction between two particles, the force on each is equal and opposite to the force on the other and is directed along a line joining them. We get the rate of change of the angular momentum to be
\begin{equation} \label{EqTorque.2} \frac{{\text d}{\bf A}}{{\text d}t} = {\bf \tau} = \sum_{\alpha} \, \sum_{\beta \ne \alpha} \left( {\bf x}_{\alpha} - {\bf x}_{\beta} \right) \times {\bf F}_{\alpha\beta} . \end{equation}

Hoverver, the angular momentum can be understood in different way by taking the reference point at P instead of the origin:

\begin{equation} \label{EqTorque.3} {\bf A}_P = \sum_{\alpha} \left( {\bf x}_{\alpha} -{\bf x}_{P} \right) \times m_{\alpha} {\bf v}_{\alpha} = \sum_{\alpha} \left( {\bf x}_{\alpha} -{\bf x}_{P} \right) \times m_{\alpha} \dot{\bf x}_{\alpha} . \end{equation}
For a time-independent mass, the rate of change of the angular momentum obeys the relation
\begin{equation} \label{EqTorque.4} \frac{{\text d}{\bf A}_P}{{\text d}t} = {\bf \tau}_P + M{\bf v}_{\text cm} \times {\bf v}_P , \end{equation}
where the torque τP is defined with respect to a fixed point P, xα is the position vector of αth particle in an inertial frame of reference of mass point mα, xP is the position vector of P in the inertial frame of reference, vα = dxα/dt, vP = dxP/dt, M is the total mass, and vcm is the velocity of the center of mass in the chosen inertial frame of reference.

If on other hand the angular momentum is understood as

\begin{equation} \label{EqTorque.5} {\bf A}_{PP} = \sum_{\alpha} \left( {\bf x}_{\alpha} -{\bf x}_{P} \right) \times m_{\alpha} \left( {\bf v}_{\alpha} - {\bf v}_P \right) = \sum_{\alpha} \left( {\bf x}_{\alpha} -{\bf x}_{P} \right) \times m_{\alpha} \left( \dot{\bf x}_{\alpha} - \dot{\bf x}_{P} \right) , \end{equation}
when velocities are evaluated relative to point P, the rate of change of the angular momentum becomes
\begin{equation} \label{EqTorque.6} \frac{{\text d}{\bf A}_{PP}}{{\text d}t} = {\bf \tau}_P + \left( {\bf x}_{\text cm} - {\bf x}_P \right) \times \left( - M\,\frac{{\text d} {\bf v}_P}{{\text d}t} \right) . \end{equation}
Here as in Eq.\eqref{EqTorque.4}, τP is the torque due to the forces exiting in the inertial frame of reference.
Torque Theorem: The torque is equal to the rate of change of angular momentum, Eq.\eqref{EqTorque.2}, if and only if
  • point P is the center of mass of the system;
  • point P is unaccelerated (relative to an internal frame);
  • the acceleration of point P is directed toward or away from the center of mass.

Hu has pointed out in 2011 that the equation of motion of a rolling body can also be derived without needing to know the forces acting at a point P being attached to the ground:

\begin{equation} \label{EqTorque.7} I_C\,\dot{\theta} + M\,{\bf x}_{\text cm} \times \left( \ddot{\theta} \right) = {\bf \tau} , \end{equation}
where \( \ddot{\theta} \) is the acceleration of the center of mass relative to an inertial frame. For a body rotating in a plane, the torque equation can be written as
\begin{equation} \label{EqTorque.8} {\bf \tau}_c = \frac{1}{\omega} \,\frac{\text d}{{\text d}t} \left( \frac{I_c}{2}\,\omega^2 \right) = I_c \frac{{\text d}^2 \theta}{{\text d} t^2} + \frac{\omega}{2}\, I_c , \qquad \omega = \dot{\theta} , \end{equation}
where c denotes the instantaneous center, τc and Ic are the net external torque and the moment of inertia, respectively. Recall that the moment of inertia I (which was introduced in 1673 by Christiaan Huygens) is defined as the ratio of the net angular momentum A of a system to its angular velocity ω around a principal axis, that is,
\[ I = \frac{A}{\omega} \]
In particular, the moment of inertia of the body that consists of point-masses is the sum
\[ I = \sum_{\alpha} m_{\alpha} r^2_{\alpha} . \]

Example 2: Let a uniform rod ("ladder") of mass m and length 2ℓ is leaning against a wall at some angle. Suppose that it is released from the rest and slides in the xy-plane along a smooth wall and smooth floor.

In 1744, L.Euler introduced the angular momentum (moment of momentum) L with respect to the fixed origin of an inertial frame

\[ {\bf L} = {\bf x} \times {\bf p} = {\bf x} \times m{\bf v} , \]
which for a time-independent mass obeys the relation
\[ \frac{{\text d}{\bf L}}{{\text d}t} = {\bf x} \times {\bf F} = {\bf \tau}, \tag{1.1} \]
where the torque τ is defined with respect to the origin.    ■

Example 3:    ■

 

  1. Freeman, M., Palffy-Muhoray, P., On mathematical and physical ladders, American Journal of Physics, 1985, 53, pp. 276--277.
  2. Kapranidis,S., Koo, R., Variations of the sliding ladder problem, The College Mathematics Journal, 2008, 39, No. 3, pp. 374--379.
  3. Majumdar, P.,Roy, M., Friction controlled three stage ladder sliding motion in an non-conservative system: From pre-detachment to post-detachment, The African Review of Physics, 2012,
  4. McDonald, K.T., Comments on torque analysis, 2019, Princeton University.
  5. McDonald, K.T., Torque analysis of a sliding ladder, 2019, Princeton University.
  6. Scholten, P., Simoson, A., The falling ladder paradox, The College Mathematics Journal, 1996, 27, pp. 49--54.

 

Rolling sphere

  1. Hu, Ben Yu-Kuang, Rolling asymmetric discs on an inclined plane, European Journal of Physics, 2011, 32, pp. L51--L54.
  2. McDonald, K.T., Cylinder rolling on another rolling cylinder, Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544, 2018.
  3. McDonald, K.T., Cylinder rolling inside another rolling cylinder, Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544, 2016.
  4. McDonald, K.T., Slab rolling on a rolling cylinder, Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544, 2016.
  5. Romer, R.H., Motion of a sphere on a tolted turntable, American Journal of Physics, 1981, 49, Issue 10, pp. 985--986.
  6. Welner, K., Stable circular orbits of greelymoving balls on rotating discs, American Journal of Physics, 1979, 47, Issue 11, pp. 984--986.

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions