Preface

This section studies some first order nonlinear ordinary differential equations describing the time evolution (or “motion”) of those hamiltonian systems provided with a first integral linking implicitly both variables to a motion constant. An application has been performed on the Lotka--Volterra predator-prey system, turning to a strongly nonlinear differential equation in the phase variables.

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part III of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

The EquationTrekker package is a great package for plotting and exploring phase space

Limit Cycles

Consider a system of first order autonomous ordinary differential equations in normal form
\[ \frac{{\text d} {\bf x}}{{\text d}t} = {\bf f}({\bf x} ) , \]
where
\[ {\bf x} (t) = \begin{bmatrix} x_1 (t) \\ x_2 (t) \\ \vdots \\ x_n (t) \end{bmatrix} , \qquad {\bf f} (x_1 , x_2 , \ldots , x_n , t) = \begin{bmatrix} f_1 (x_1 , x_2 , \ldots , x_n ) \\ f_2 (x_1 , x_2 , \ldots , x_2 ) \\ \vdots \\ f_n (x_1 , x_2 , \ldots , x_n ) \end{bmatrix} \]
are n-column vectors. In engineering and physics, it is a custom to denote a derivative with respect to time variable t by dot: \( \dot{\bf x} = {\text d}{\bf x} / {\text d} t. \)

If an initial position of the vector \( {\bf x} (t) \) is known, we get an initial value problem:

\[ \dot{\bf x} \equiv \frac{{\text d} {\bf x}}{{\text d}t} = {\bf f}({\bf x} ) , \qquad {\bf x} (t_0 ) = {\bf x}_0 , \]
where \( {\bf x}_0 \) is a given column vector.

 

 

2.3.5. Limited Circles

Liénard's Theorem: A Liénard system \( \ddot{x} +f(x)\,\dot{x} + g(x) =0 \) has a unique and stable limit cycle surrounding the origin if it satisfies the following additional properties:

 

Example 1: Consider the undamped Duffing equation
\[ \ddot{x} +x +0.1\,x^3 =0, \]
which we transfer into the first-order system of equations
\[ v= \dot{\bf x} \qquad \dot{v} = -x-0.1\,x^3 . \]
dirfield = VectorPlot[{v, -x - 0.1*x^3}, {x, -4, 4}, {v, -5, 5}, Prolog -> {Thickness[0.001]},
Axes -> True, AspectRatio -> 1, VectorPoints -> 15, AxesLabel -> {x, v}]
There is a strong suggestion of periodic motion, in the way that the arrows circle around. Now we will construct some solutions and then display them with the direction field. We define the equation first.
duff[x0_, v0_] := {x'[t] == v[t], v'[t] == -x[t] - 0.1*(x[t])^3, x[0] == x0, v[0] == v0}
As before we define a function which will produce, but not display, the phase plane plot for given initial position \( (x_0, y_0 ) . \)
graph[x0_, v0_] :=
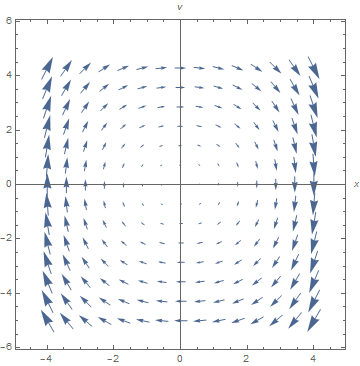
Module[{xans, vans},
{xans, vans} = {x[t], v[t]} /. Flatten[NDSolve[duff[x0, v0], {x[t], v[t]}, {t, 0, 8}]];
ParametricPlot[{xans, vans}, {t, 0, 8}, PlotRange -> {{-5.1, 5.1}, {-5, 5}},
AxesLabel -> {"x", "v"}, AspectRatio -> 1, DisplayFunction -> Identity,
PlotStyle -> RGBColor[1, 0, 0]]];
We try this for one initial condition
Show[graph[3.5, 0], DisplayFunction -> $DisplayFunction]
We get a closed curve, which is the signature of a periodic solution. Now we construct a family of solutions, using the list of initial conditions given below.
initlist = {{0.5, 0}, {1, 0}, {1.5, 0}, {2, 0}, {2.5, 0}, {3, 0}, {3.5, 0}, {4, 0}};
Now we produce all of the graphs without showing them individually
Module[{i, x0temp, v0temp, pair, newgraph}, graphlist = {};
Do[pair = initlist[[i]];
x0temp = First[pair]; v0temp = Last[pair]; newgraph = graph[x0temp, v0temp];
graphlist = Append[graphlist, newgraph], {i, 1, 8}]]
Now we plot them.
solgraph = Show[graphlist, DisplayFunction -> $DisplayFunction]
Finally we combine the solutions and the direction field.
Show[dirfield, solgraph]
Our graph shows that this interesting system has the property that every initial condition gives rise to a periodic solution. Of course if we remember that the equations describe an undamped spring mass system, such behavior is not so surprising. The equilibrium point at the origin is enclosed by the periodic solutions, but the system does not go to the equilibrium point. If we introduced some damping, all of the closed curves would change to spirals which would asymptotically approach the equilibrium point.     ■

 

Example 2: Consider the system of nonlinear differential equations
\[ \begin{split} \dot{x} &= -y - x^2 , \\ \dot{y} &= 2x - y^3 . \end{split} \]
According to Mathematica, the iven system has two critical points: the origin and
\[ \left( - 2^{1/5} , - 2^{2/5} \right) \approx \left( -1.1487 , - 1.31951 \right) . \]
Solve[2*x + x^6 == 0, x]
{{x -> 0}, {x -> (-2)^( 1/5)}, {x -> -2^(1/5)}, {x -> -(-1)^(2/5) 2^(1/5)}, {x -> (-1)^( 3/5) 2^(1/5)}, {x -> -(-1)^(4/5) 2^(1/5)}}
NSolve[2*x + x^6 == 0, x]
{{x -> -1.1487}, {x -> -0.354967 - 1.09248 I}, {x -> -0.354967 + 1.09248 I}, {x -> 0.}, {x -> 0.929316 - 0.675188 I}, {x -> 0.929316 + 0.675188 I}}
Upon plotting the direction field, we see that the origin is the center, but (-1.1487, -1.3195) is an unstable saddle point.



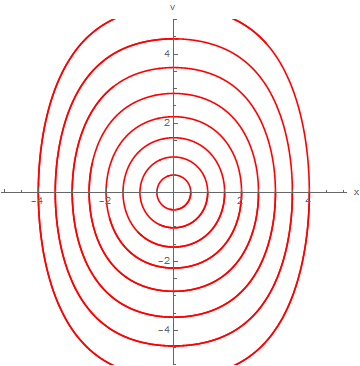
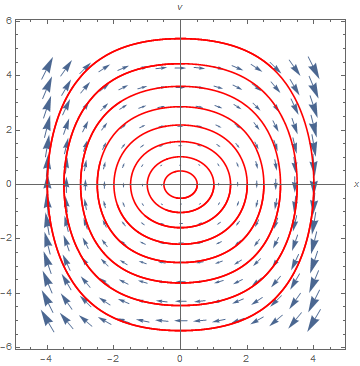
StreamPlot[{-y - x^2, 2*x - y^3}, {x, -2.5, 2.5}, {y, -2.5, 2.5}, StreamScale -> Large]
Then we solve the system numerically and plot x versus y to identify the limit cycle.



A = StreamPlot[{-y - x^2, 2*x - y^3}, {x, -2.5, 2.5}, {y, -2.5, 2.5}, StreamScale -> Large, PlotRange -> {{3, -3}, {3, -3}}];
sol = NDSolve[{x'[t] == -y[t] - (x[t])^2, y'[t] == 2*x[t] - (y[t])^3, x[0] == 1, y[0] == 1}, {x, y}, {t, 0, 150}];
B = ParametricPlot[Evaluate[{x[t], y[t]} /. sol], {t, -.1, 100}, PlotStyle -> {Blue, Thick}, PlotRange -> {{3, -3}, {3, -3}}] ; B2 = ParametricPlot[Evaluate[{x[t], y[t]} /. sol], {t, 95, 100}, PlotStyle -> {Red, Thickness[.012]}, PlotRange -> {{3, -3}, {3, -3}}];
Show[A, B, B2, PlotRange -> {{3, -3}, {3, -3}}]
Show[A, B, B2, PlotRange -> {{.5, -.5}, {.5, -.5}}]
    ■

 

Example 3: Consider the Rabinovich-- Fabrikant system
\begin{equation} \label{EqChaos.1} \begin{split} \dot{x} &= y \left( z-1 + x^2 \right) + \gamma \,x , \\ \dot{y} &= x \left( 3z + 1 - x^2 \right) + \gamma \, y , \\ \dot{z} &= -2z \left( \alpha + xy \right) , \end{split} \end{equation}
where α and γ are constants that control the evolution of the system.
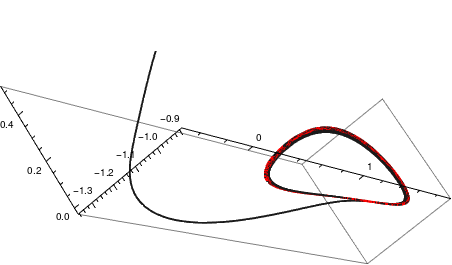
      We plot solutions to RF system when α = 1.14 and γ = 0.1 with the initial conditions
\[ x(0) = -1, \quad y(0) = 0, \quad z(0) = 0.5. \]
The corresponding limit circle (in red color) is clearly visible.
a = 1.14; gamma = 0.1;
sol = NDSolve[{x'[t] == y[t]*(z[t] - 1 + (x[t])^2) + gamma*x[t], y'[t] == x[t]*(3*z[t] + 1 - (x[t])^2) + gamma*y[t], z'[t] == -2*z[t]*(a + x[t]*y[t]), x[0] == -1, y[0] == 0, z[0] == 0.5}, {x, y, z}, {t, 0, 200}];
pp = ParametricPlot3D[ Evaluate[{x[t], y[t], z[t]} /. sol], {t, 0, 100}, PlotRange -> All, PlotTheme -> "Monochrome"];
lim = ParametricPlot3D[ Evaluate[{x[t], y[t], z[t]} /. sol], {t, 35, 100}, PlotRange -> All, PlotTheme -> "Monochrome", PlotStyle -> {Red, Thickness[.005]}];
Show[lim, pp]
       Rabinovich–Fabrikant system            Mathematica code

    ■

 

 

2.3.6. Applications

 

 


F[x_, y_] := -y^3;
G[x_, y_] := x^3;
sol = NDSolve[{x'[t] == F[x[t], y[t]], y'[t] == G[x[t], y[t]],
x[0] == 1, y[0] == 0}, {x, y}, {t, 0, 3*Pi},
WorkingPrecision -> 20]
ParametricPlot[Evaluate[{x[t], y[t]}] /. sol, {t, 0, 3*Pi}]

Out[11]=
{{x -> InterpolatingFunction[{{0, 9.4247779607693797154}}, <>],
    y -> InterpolatingFunction[{{0, 9.4247779607693797154}}, <>]}}
X[t_] := Evaluate[x[t] /. sol]
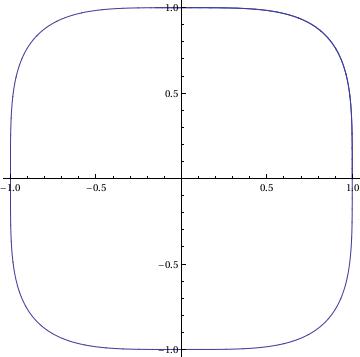
Y[t_] := Evaluate[y[t] /. sol]
fns[t_] := {X[t], Y[t]};
len := Length[fns[t]];
Plot[Evaluate[fns[t]], {t, 0, 3*Pi}]

V. Pendulum Equation

 

fx = Function[{x, y}, y]; fy = Function[{x, y}, -Sin[x] - 0.25*y]
portrait =
StreamPlot[{fx[x, y], fy[x, y]}, {x, -6, 6}, {y, -3, 3},
AspectRatio -> Automatic]
solution =
Function[point,
Function @@ {t, ({x[t], y[t]} /.
NDSolve[{x'[t] == fx[x[t], y[t]], y'[t] == fy[x[t], y[t]],
Thred[{x[time], y[time]} == point]}, {x, y}, {t, time,
time + 40}])[[1]]}]

Out[12]=
Function[point,
Function @@ {t, ({x[t], y[t]} /.
NDSolve[{Derivative[1][x][t] == fx[x[t], y[t]],
Derivative[1][y][t] == fy[x[t], y[t]],
Thred[{x[time], y[time]} == point]}, {x, y}, {t, time,
time + 40}])[[1]]}]

 

 

 

 

V. van der Pol Equation

splot = StreamPlot[{y, (1 - x^2) y - x}, {x, -4, 4}, {y, -3, 3}, StreamColorFunction -> "Rainbow"]; Manipulate[ Show[splot, ParametricPlot[ Evaluate[ First[{x[t], y[t]} /. NDSolve[{x'[t] == y[t], y'[t] == y[t] (1 - x[t]^2) - x[t] + 0.5 Cos[1.1 t], Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0, T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}}, Locator}, SaveDefinitions -> True]
Or just to show off (again a rip off from the documentation)
splot = LineIntegralConvolutionPlot[{{y, (1 - x^2) y - x}, {"noise", 1000, 1000}}, {x, -4, 4}, {y, -3, 3}, ColorFunction -> "BeachColors", LightingAngle -> 0, LineIntegralConvolutionScale -> 3, Frame -> False]; Manipulate[ Show[splot, ParametricPlot[ Evaluate[ First[{x[t], y[t]} /. NDSolve[{x'[t] == y[t], y'[t] == y[t] (1 - x[t]^2) - x[t]+0.5 Cos[1.1 t], Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0, T}, PlotStyle -> White]], {{T, 20}, 1, 100}, {{point, {3, 0}}, Locator}, SaveDefinitions -> True]
You can solve the equation with (you might want to change the initial conditions) :
sol[t_] = NDSolve[{x''[t] - (1 - x[t]^2) x'[t] + x[t] == 0.5 Cos[1.1 t], x[0] == 0, x'[0] == 1}, x[t], {t, 0, 10}][[1, 1, 2]]
Now you can use the solution as any other function; in particular, you can plot it versus its derivative :
ParametricPlot[{sol[t], sol'[t]}, {t, 0, 10}]

 

  1. D’Acunto M., Determination of limit cycles for a modified van der Pol oscillator. Mechanics Research Communications, 2006, 33:93–100. [doi:10.1016/j.mechrescom.2005.06.012]
  2. Gottlieb, H.P.W., 2006. Harmonic balance approach to limit cycles for nonlinear jerk equations. Journal of Sound and Vibration, 297:243–250. [doi:10.1016/j.jsv.2006.03.047]
  3. He, J.H., 2003. Determination of limit cycles for strongly nonlinear oscillators. Physical Review Letters, 90(17), Article No. 174301.
  4. He, J.H., 2006a. Determination of limit cycles for strongly nonlinear oscillators. Physic Review Letter, 90:174–181.

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions