Preface
This section concerns about numerical solutions to the Laplace equation.
Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part VI of the course APMA0340
Introduction to Linear Algebra with Mathematica
Glossary
Numerical Solutions to Laplace Equations
In this section, we discuss some algorithms to solve numerically boundary value porblems for Laplace's equation (∇2u = 0), Poisson's equation (∇2u = g(x,y)), and Helmholtz's equation (∇2u + k(x,y) u = g(x,y)). We start with the Dirichlet problem in a rectangle \( R = [0,a] \times [0,b] . \)
The Laplacian operator must be expressed in a discrete form suitable for numerical computations. The formula for approximating \( f'' (x) \) is obtained from
l1 = Graphics[{Thick,Line[{{0,1},{8,1}}]}];
l2 = Graphics[{Thick,Line[{{0,2},{8,2}}]}];
l3 = Graphics[{Thick,Line[{{0,3},{8,3}}]}];
l4 = Graphics[{Thick,Line[{{0,4},{8,4}}]}];
l5 = Graphics[{Thick,Line[{{0,5},{8,5}}]}];
la0 = Graphics[{Thick,Line[{{0,0},{0,5}}]}];
la1 = Graphics[{Thick,Line[{{1,0},{1,5}}]}];
la2 = Graphics[{Thick,Line[{{2,0},{2,5}}]}];
la3 = Graphics[{Thick,Line[{{3,0},{3,5}}]}];
la4 = Graphics[{Thick,Line[{{4,0},{4,5}}]}];
la5 = Graphics[{Thick,Line[{{5,0},{5,5}}]}];
la6 = Graphics[{Thick,Line[{{6,0},{6,5}}]}];
la7 = Graphics[{Thick,Line[{{7,0},{7,5}}]}];
la8 = Graphics[{Thick,Line[{{8,0},{8,5}}]}];
d0 = Graphics[{Orange, Disk[{4, 3}, 0.15]}];
d1 = Graphics[{Orange, Disk[{4, 4}, 0.15]}];
d2 = Graphics[{Orange, Disk[{4, 2}, 0.15]}];
d3 = Graphics[{Orange, Disk[{3, 3}, 0.15]}];
d4 = Graphics[{Orange, Disk[{5, 3}, 0.15]}];
r1 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(x\), \(i\)]\)", Medium], {4, -0.3}]];
r2 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(x\), \(i-1\)]\)", Medium], {3, -0.3}]];
r3 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(x\), \(i+1\)]\)", Medium], {5, -0.3}]];
r4 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(x\), \(n-1\)]\)", Medium], {7, -0.3}]];
r5 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(x\), \(n\)]\)", Medium], {8, -0.3}]];
r6 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(x\), \(2\)]\)", Medium], {1, -0.3}]];
r7 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(x\), \(1\)]\)", Medium], {0, -0.3}]];
t0 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(y\), \(1\)]\)", Medium], {-0.3, 0}]];
t1 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(y\), \(j-1\)]\)", Medium], {-0.4, 2}]];
t2 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(y\), \(j\)]\)", Medium], {-0.3, 3}]];
t3 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(y\), \(j+1\)]\)", Medium], {-0.4, 4}]];
t4 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(y\), \(m\)]\)", Medium], {-0.3, 5}]];
Show[l0,l1,l2,l3,l4,l5,la0,la1,la2,la3,la4,la5,la6,la7,la8,d0, d1, d2, d3, d4, r1,r2,r3,r4,r5,r6,r7, t0,t1,t2,t3,t4]
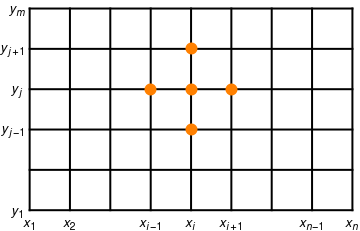
To solve Laplace's equation, we impose the approximation
l2 = Graphics[{Thick,Line[{{0,-2},{0,2}}]}];
d0 = Graphics[{Red, Disk[{0, 0}, 0.1]}];
d1 = Graphics[{Blue, Disk[{0, 2}, 0.1]}];
d2 = Graphics[{Blue, Disk[{0, -2}, 0.1]}];
d3 = Graphics[{Blue, Disk[{2, 0}, 0.1]}];
d4 = Graphics[{Blue, Disk[{-2, 0}, 0.1]}];
t0 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(-4 u\), \(i,j\)]\)", Medium], {0.4, -0.2}]];
t1 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(i-1,j\)]\)", Medium], {-2.2, -0.2}]];
t2 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(i+1,j\)]\)", Medium], {2.2, -0.2}]];
t3 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(i,j+1\)]\)", Medium], {0.2, 2.2}]];
t4 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(i,j-1\)]\)", Medium], {-0.2, -2.2}]];
Show[l1,l2,d0,d1,d2,d3,d4, t0,t1,t2,t3,t4]
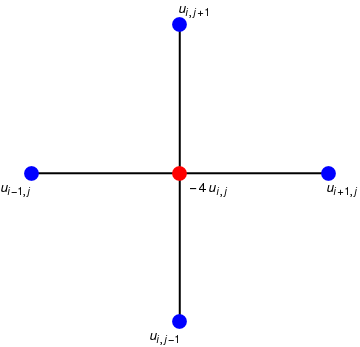
Assume that the values u(x,y) are known at the following boundary grid points:
Program (Dirichlet method for Laplace's equation): to approximate the solution of \( u_{xx} + u_{yy} =0 \) over \( R = \{\,(x,y) \,:\, 0 \le x \le a , \ 0 \le y \le b \) with \( u(x,0) = f_0 (x), \ u(x,b) = f_b (x) , \) for 0 ≤ x ≤ a;, and \( u(0,y) = g_0 (y), \ u(a,y) = g_a (y) , \) for 0 ≤ y ≤ b. It is assumed that Δx = Δy = h and that integers n and m exist so that a=nh and b=mh.
function U=dirichlet(f0,fb,g0,ga,a,b,h,tol,max1)
% Input -- f0,fb,g0,ga are boundary functions input as a strings
% -- a and b right end points of [0,a] and [0,b]
% -- h step size
% -- tol is the tolerance
% -- max1
% Output -- U solution matrix;
% Initialize parameters and U
n=fix(a/h)+1;
m=fix(b/h)+1;
ave=(a*(feval(f0,0)+feval(fb,0))+b*(feval(g0,0)+feval(ga,0)))/(2*a+2*b);
U=ave*ones(n,m);
% Boundary conditions
U(1,1:m)=feval(g0,0:h:(m-1)*h))';
U(n,1:m)=feval(ga,0:h:(m-1)*h))';
U(1:n,1)=feval(fa,0:h:(n-1)*h))';
U(1:n,m)=feval(fb,0:h:(n-1)*h))';
U(1,1)=(U(1,2)+U(2,1))/2;
U(1,m)=(U(i,m-1)+U(2,m))/2;
U(n,1)=(U(n-1,1)+U(n,2))/2;
U(n,m)=(U(n-1,m)+U(n,m-1))/2;
% SQR parameter
w=4/(2+sqrt(4-(cos(pi/(n-1))+cos(pi/(m-1)))^2));
% Refine approximations and sweep operator throughout the grid
err=1;
cnt=0;
while((err>tol)&(cnt<=max1))
err=0;
for j=2:m-1
for i=2:n-1
relx=w*(U(i,j+1)+U(i,j-1)+U(i+1,j)+U(i-1,j)-4*U(i,j))/4;
U(i,j)=U(i,j)+relx;
if (err<=abs(relx))
err=abs(relx);
end
end
end
cnt=cnt+1;
end
U=flipud(U');
l1 = Graphics[{Thick,Line[{{0,0},{0,8}}]}];
l2 = Graphics[{Thick,Line[{{0,8},{10,8}}]}];
l3 = Graphics[{Thick,Line[{{10,0},{10,8}}]}];
d0 = Graphics[{Blue, Disk[{0, 2}, 0.15]}];
d1 = Graphics[{Blue, Disk[{0, 4}, 0.15]}];
d2 = Graphics[{Blue, Disk[{0, 6}, 0.15]}];
d3 = Graphics[{Blue, Disk[{2, 0}, 0.15]}];
d4 = Graphics[{Blue, Disk[{2, 2}, 0.15]}];
d5 = Graphics[{Blue, Disk[{2, 4}, 0.15]}];
d6 = Graphics[{Blue, Disk[{2, 6}, 0.15]}];
d7 = Graphics[{Blue, Disk[{2, 8}, 0.15]}];
d8 = Graphics[{Blue, Disk[{4, 0}, 0.15]}];
d9 = Graphics[{Blue, Disk[{4, 2}, 0.15]}];
d10 = Graphics[{Blue, Disk[{4, 4}, 0.15]}];
d11 = Graphics[{Blue, Disk[{4, 6}, 0.15]}];
d12 = Graphics[{Blue, Disk[{4, 8}, 0.15]}];
d13 = Graphics[{Blue, Disk[{6, 0}, 0.15]}];
d14 = Graphics[{Blue, Disk[{6, 2}, 0.15]}];
d15 = Graphics[{Blue, Disk[{6, 4}, 0.15]}];
d16 = Graphics[{Blue, Disk[{6, 6}, 0.15]}];
d17 = Graphics[{Blue, Disk[{6, 8}, 0.15]}];
d18 = Graphics[{Blue, Disk[{8, 0}, 0.15]}];
d19 = Graphics[{Blue, Disk[{8, 2}, 0.15]}];
d20 = Graphics[{Blue, Disk[{8, 4}, 0.15]}];
d21 = Graphics[{Blue, Disk[{8, 6}, 0.15]}];
d22 = Graphics[{Blue, Disk[{8, 8}, 0.15]}];
d23 = Graphics[{Blue, Disk[{10, 2}, 0.15]}];
d24 = Graphics[{Blue, Disk[{10, 4}, 0.15]}];
d25 = Graphics[{Blue, Disk[{10, 6}, 0.15]}];
r1 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(2,1\)]\)", Medium], {2, -0.5}]];
r2 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(3,1\)]\)", Medium], {4, -0.5}]];
r3 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(4,1\)]\)", Medium], {6, -0.5}]];
r4 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(5,1\)]\)", Medium], {8, -0.5}]];
r5 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(1,2\)]\)", Medium], {-0.8, 2.0}]];
r6 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(1,3\)]\)", Medium], {-0.8, 4}]];
r7 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(1,4\)]\)", Medium], {-0.8, 6}]];
r8 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(6,2\)]\)", Medium], {10.8, 2}]]; r9 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(6,3\)]\)", Medium], {10.8, 4}]];
r10 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(6,4\)]\)", Medium], {10.8, 6}]];
r11 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(1,4\)]\)", Medium], {2, 8.6}]]; r12 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(6,2\)]\)", Medium], {4, 8.6}]];
r13 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(6,2\)]\)", Medium], {6, 8.6}]];
r14 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(u\), \(6,2\)]\)", Medium], {8, 8.6}]];
t0 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(1\)]\)", Medium], {2, 1.5}]];
t1 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(2\)]\)", Medium], {4, 1.5}]];
t2 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(3\)]\)", Medium], {6, 1.5}]];
t3 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(4\)]\)", Medium], {8, 1.5}]];
t4 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(5\)]\)", Medium], {2, 3.5}]];
t5 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(6\)]\)", Medium], {4, 3.5}]];
t6 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(7\)]\)", Medium], {6, 3.5}]];
t7 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(8\)]\)", Medium], {8, 3.5}]];
t8 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(9\)]\)", Medium], {2, 5.5}]];
t9 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(10\)]\)", Medium], {4, 5.5}]];
t10 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(11\)]\)", Medium], {6, 5.5}]];
t11 = Graphics[ Text[Style["\!\(\*SubscriptBox[\(p\), \(12\)]\)", Medium], {8, 5.5}]];
Show[l0,l1,l2,l3,d0,d1, d2, d3, d4,d5,d6,d7,d8,d9,d10,d11,d12,d13,d14,d15,d16,d17,d18,d19,d20,d21,d22,d23,d24,d25, r1,r2,r3,r4,r5,r6,r7, t0,t1,t2,t3,t4,t5,t6,t7,t8,t9,t10,t11]
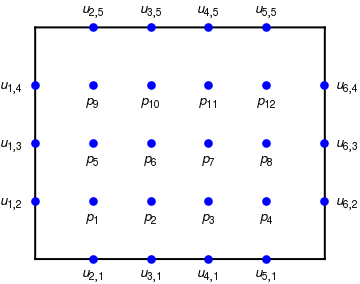
For example, suppose that the region is a rectangle with n=6 and m=5, and that the unknown values of u(xi,yj) at the twelve interior grid points are labeled p1, p2, ... ,p12 and positioned in the grid as shown in the figure above. The Laplacian computational formula is applied at each of the interior grid points, and the result is the system A p = b of twelve linear equations:
- Amir, M.J., Yaseen, M., Iqbal, R., Exact solutions of Laplace equation by differential transform method,
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions