Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part V of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

Preface

This section studies some first order nonlinear ordinary differential equations describing the time evolution (or “motion”) of spreading some deceases, including HIV, SIR, SEIR, and others.

HIV Models

The interaction of the HIV-1 virus with the body's immune system can be modeled by a system of differential equations similar to a predator-prey system. After an individual is infected with the HIV-1 virus, the amount of the virus in the bloodstream rises dramatically and the person will often suffer from flu-like symptoms. However, these symptoms will disappear after a period of weeks or months as the body begins to manufacture antibodies against the virus. Tests have been developed to determine the presence of HIV-1 antibodies. If a individual has such antibodies, then they are said to be HIV-1 positive. Once infected with the HIV-1 virus, it can be years before an HIV-positive patient exhibits the full symptoms of AIDS. The body's immune system fights the HIV-1 virus with white blood cells. The CD4-positive T-helper cells, a specific type of white blood cell, is especially important since it helps other cells fight the virus. However, the HIV-1 virus can destroy CD4-positive T-helper cells.

We can develop a system of differential equations to better understand the dynamics of the HIV-1 virus. Let V=V(t) be the population of the HIV-1 virus at time t. We will assume that the virus concentration is governed by the following differential equation,

\[ \frac{{\text d} V}{{\text d} t} \equiv \dot{P} = P - c\, V . \]
The first term in the right-hand side, P is some function of t that determines the rate at which new viral particles are created. The term −cV is the death rate for the virus. If someone discovers a drug that blocks the creation of new HIV-1 virions, then P would be zero and the virions would clear the body at the following rate,
\[ \dot{P} = - c\, V , \]
and \( V(t) = V_0 e^{-ct} , \) where V0 is the initial viral population.

Now let us consider a model for the concentration of T=T(t) of (uninfected) CD4-positive T-helper cells,

\[ \dot{T} = s + pT \left( 1- \frac{T}{T_{\max}} \right) - d_T T . \]
As usual, dot denotes derivative with respect to time t: \( \dot{T} = {\text d}T / {\text d} t . \) The constant s represents the rate at which T cells are created from sources in the body, such as the thymus. New CD4-positive T-helper cells can also be created from the proliferation of existing CD4-positive T-helper cells, and the second term in the equation represents the logistic growth of the T cells, where p is the maximum proliferation rate and Tmax is the T cell population density where proliferation ceases. Finally, dT is the death rate of the T cells.

The above equation has two equilibrium solutions:

\[ T = \frac{T_{\max}}{2p} \left( p- d_T \pm \sqrt{\frac{4ps}{T_{\max}} + \left( p -d_T \right)^2} \right) . \]

Like the influenza virus, the HIV-1 virus is an RNA virus. An RNA virus cannot reproduce on its own and must use the DNA from a host cell. To do this, the virus attaches itself to a CD4-positive T-helper cell and injects its RNA into the cell. This way the virus can use the T-cell's DNA to replicate itself using a process called reverse transcription, where a DNA copy of the virus's RNA is made. New virus particles are created, and the T cell eventually bursts releasing the virus into the body. If we let I be the concentration of infected T-cells, we can model this process with the following system of equations,

\begin{align*} \dot{I} &= k\,TV - \delta\,I , \\ \dot{V} &= N\delta \, I -c\, V , \end{align*}
where δ is the rate of loss of the virus producing T cells and N is the number of version's produced per infected T cell during its lifetime. The term k TV tells us the rate at which the HIV-1 virus infects T cells. This is the same idea as modeling how predators interact with prey in a Lotka--Volterra model. Thus, our complete model becomes
\begin{align*} \dot{T} &= s + pT \left( 1- \frac{T}{T_{\max}} \right) - d_T T -k\,TV , \\ \dot{I} &= k\,TV - \delta\,I , \\ \dot{V} &= N\delta \, I -c\, V . \end{align*}

The above system has one nontrivial critical point:

\[ T = \frac{c}{k\,N} , \quad I = \frac{k^2 N^2 s T_{\max} + ckN p T_{\max} - cd_T kN T_{\max} -c^2 p }{\delta k^2 N^2 T_{\max} } , \quad V = \frac{k^2 N^2 s T_{\max} + ckN p T_{\max} - cd_T kN T_{\max} -c^2 p }{ck^2 N T_{\max}} . \]
Then we calculate the Jacobian matrix:
JacobianMatrix[f_List?VectorQ, x_List] :=
Outer[D, f, x] /; Equal @@ (Dimensions /@ {f, x})
a = {s + p*T*(1 - T/tmax) - dt*T - k*T*V, k*T*V - d*i, n*d*i - c*V}
b = {T, i, V}
JacobianMatrix[a, b] // MatrixForm
\[ {\bf J} = \begin{bmatrix} p \left( 1- \frac{T}{T_{\max}} \right) -d_T - \frac{p\,T}{T_{\max}} - k\,V & 0 & -k\,T \\ k\,V & -\delta & k\,T \\ 0 & \delta N & -c \end{bmatrix} . \]
At this critical point, the Jacobian becomes
\[ {\bf J} (\mbox{critical}) = \begin{bmatrix} -\frac{kNs}{c} -\frac{cp}{kN T_{\max}} & 0 & -\frac{c}{N} \\ p + \frac{kNs}{c} - d_T & -\delta & \frac{c}{N} \\ 0 & \delta N & -c \end{bmatrix} . \]

One class of drugs that HIV infected patients receive are reverse transcriptase (RT) inhibitors. RT inhibitors block the action of reverse transcription and prevent the virus from duplicating. If one could find the perfect RT inhibitor, then k=0 and our system becomes

\begin{align*} \dot{T} &= s + pT \left( 1- \frac{T}{T_{\max}} \right) - d_T T , \\ \dot{I} &= - \delta\,I , \\ \dot{V} &= N\delta \, I -c\, V . \end{align*}

Unfortunately, no one has discovered a perfect RT inhibitor, so we will need to modify the system to account for the effectiveness of the RT inhibitor. We can accomplish this by adding an effectiveness factor 1-η to the k VT term. Our system now becomes

\begin{align*} \dot{T} &= s + pT \left( 1- \frac{T}{T_{\max}} \right) - d_T T -k\left( 1-\eta \right) TV , \\ \dot{I} &= k\left( 1-\eta \right) TV - \delta\,I , \\ \dot{V} &= N\delta \, I -c\, V . \end{align*}

If η=1, then the RT inhibitor is completely effective. On the other hand, if η=0, then the RT inhibitor is completely ineffective. We now have a model for how the HIV-1 virus interacts with the immune system. Researchers can use data to estimate the parameters and see exactly what types of solutions are possible.

Example: In this model, the fox population is divided into three classes, all of which are measured in population density (foxes/km²), namely, susceptibles, denoted by X, are foxes that are currently healthy but are susceptible to catching the virus; infected, denoted by Y, are foxes that have caught the virus but are not yet capable of passing on the virus; and finally, infectious, denoted by Z, are foxes that are capable of infecting the susceptibles. The relevant equations for the fox rabies epidemic are
\[ \begin{split} \dot{X} &= a\,X - \left( b+ \gamma N \right) X - \beta\,X\,Z, \\ \dot{Y} &= \beta\,X\,Z - \left( \sigma + b + \gamma N \right) Y , \\ \dot{Z} &= \sigma\,Y - \left( \alpha + b + \gamma N \right) Z , \end{split} \]
with N = X + Y + Z being the total fox density. Note that the above model has no category of recovered immune foxes because very few, if any, survive after acquiring the rabies virus. The meaning of the coefficients and their estimated values are given in the following table.
Meaning of coefficients
Symbol Meaning Value
a average per capita birth rate of foxes 1 yr-1
b average per capita intrinsic death rate 0.5 yr-1
β rabies transmission coefficient 79.67 km² yr-1
σ 1/σ is the average latent period (∼ 28 to 30 days) 13 yr-1
α death rate of rabid foxes (average life expectancy ∼ 5 days) 73 yr-1
γ &gammalN represents increased death rate when N is large enough to deplete the food supply 0.1--5 km²yr-1
    ■

SIR and SIRS Models

This topic describes the differential equations that govern the classic deterministic SIR and SIRS compartmental models and describes how to configure EMOD, an agent-based stochastic model, to simulate an SIR/SIRS epidemic. In SIR models, individuals in the recovered state gain total immunity to the pathogen; in SIRS models, that immunity wanes over time and individuals can become reinfected. The EMOD generic simulation uses an SEIR-like disease model by default. You can modify the default SEIR model to an SIR model by turning off the incubation period.

As the first step in the modeling process, we identify the independent and dependent variables. The independent variable is time t, measured in days. We consider two related sets of dependent variables. The first set of dependent variables counts people in each of the groups, each as a function of time:

The second set of dependent variables represents the fraction of the total population in each of the three categories. So, if N is the total population (7,900,000 in our example), we have
Example: We consider transmission dynamics of a Childhood disease outbreak in a community with direct inflow of susceptible and vaccinated new-born. Childhood diseases are increasingly becoming the most common form of infectious diseases. These diseases include measles, mumps, Influenza, smallpox, chicken pox, Rubella, Polio etc., which take special interest to children under-five years who are born highly susceptible. The following SEIR model has four epidemiological compartments: the susceptible S, an exposed E, an infective I, and a recovered group R, i.e. the vaccinated and treated group who poses permanent immunity to the disease. We assume the vaccines are 100% efficient and death rates μ due to causes other than the disease in the compartments are not equal to births, leading to varying population size N. People who are recruited into the community with e the proportion of susceptible that are vaccinated as P (with 0 < P < 1) and take the rest to be susceptible. We assume the vaccination rate as π. A susceptible person will progress into the exposed group by being in contact with an infective individual, estimated by a contact rate β2 or through contact with an exposed individual, estimated by a contact rate β1. An exposed individual Progresses from exposed to the infective compartment at a rate δ. An infective child progresses from infected to the recovered group due to treatment at a rate γ. We also assume α to be death rate due to disease infection.

The resulting differential equations for the model are

\begin{align*} \frac{{\text d}S}{{\text d}t} &= \left( 1- P \right) \pi N - \frac{\beta_1 E + \beta_2 I}{N}\,S - \mu\, S, \\ \frac{{\text d}E}{{\text d}t} &= \frac{\beta_1 E + \beta_2 I}{N}\, S - \left( \delta + \mu \right) E, \\ \frac{{\text d}I}{{\text d}t} &= \delta\, E - \left( \alpha + \gamma + \mu \right) I, \\ \frac{{\text d}R}{{\text d}t} &= P\pi \,N + \gamma \,I - \mu\,R, \end{align*}
subject to the initial conditions
\[ S(0) = s_) , \quad E(0) = E_0 , \quad I(0) = I_0 , \quad R(0) = R_) . \]
We also assume that all coefficients of the system, μ, β1, β2, π, α, γ, and δ are constants, and N = S + E + I + R. Adding the above equations, we obtain
\[ \frac{{\text d}N}{{\text d}t} = \left( \pi - \mu \right) N - \alpha\,I, \]
which exhibits a varying population size with deaths due to fatal diseases.     ■

Tumor-immune Models

A tumor, an abnormal growth of body tissue, may be malignant or benign. A malignant tumor can turn into cancer, which is difficult to cure once metastasized. With the immune system, the host usually controls the growth and division of tumor cells to prevent from becoming cancerous. In this process, the interaction between tumors and immune system is a complex phenomenon difficult to be understood completely. There are known many mathematical models to predict this interaction.

It is known that tumor cells can biochemically stimulate the production of immune cells (commonly called effector cells) such as cytotoxic T-cells, macrophages, and natural killer cells. Effector cells are cytotoxic to tumor cells and will retard the growth of tumor cells. Therefore, the interaction between tumor cells and effector cells can be regarded as an analog of the "predator-prey" interaction, where the predator is effector cells and the prey is tumor cells. On the other hand, effector cells can be neutralized by tumor cells, which means that the two types of cells are "competitive". The coexistence of these two relationships leads to the complexity of the dynamic behavior of resulting models.

The interaction between cells and effector cells are determined by three major factors: the malignant potential of a tumor, the tumor's antigenicity, and the immune response of the host. The malignant potential of a tumor represents its ability to metastasize, escape, and destroy the immune system. The degree of antigenicity of a tumor is defined as the initial size of the effector cell population that can be stimulated upon introduction of the antigen, which is associated with the tumor. It varies greatly from cancer to cancer and from patient to patient. Larger values represent tumor cells that present a well recognized antigen while small values represent tumor cells that present a weak antigen. The tumor response reflects the suppression of tumor growth by the host's immune system, where effector cells are recruited due to the presence of tumor cells. The recruitment of effector cells corresponding to the presence of tumor cells depends on tumor's antigenicity of tumor cells. The classical tumor-immune interaction models were first proposed by Kuznetsov et al. (1994) and Kirschner and Panetta (1998).

Following Li at al. (2021), we consider the following (normalized) model

\begin{equation} \label{EqTumor.1} \begin{split} \frac{{\text d}E}{{\text d}t} &= s + c\,T - \beta\, E\cdot T - E , \\ \frac{{\text d}T}{{\text d}t} &= r\, T \left( 1 - T - \frac{\alpha \, E}{1 + \varepsilon\, T} \right) , \end{split} \end{equation}
where E(t) and T(t) denote the numbers (or concentrations) of effector cells and tumor cells at time t, respectively. All coefficients in Eq.\eqref{EqTumor.1} are assumed to be positive.

Disregarding the last term in second equation of \eqref{EqTumor.1}, we get

\[ \frac{{\text d}T}{{\text d}t} \leqslant r\, T \left( 1 - T \right) \qquad \Longrightarrow \qquad \lim_{t\to \infty} \sup T(t) \leqslant 1 . \]
This combines with the first equation an estimate: \( \displaystyle \quad \lim_{t\to \infty} \sup E(t) \leqslant s+ c . \) Moreover, the set
\[ \Omega = \left\{ (E, T) \in \mathbb{R}^2_{+} \, : \ E \leqslant s + c , \quad T \leqslant 1 \right\} \]
is positively invariant for system \eqref{EqTumor.1}.

Obviously, system \eqref{EqTumor.1} always has equilibrium at P₀(s, 0), which is referred to as the tumor-free equilibrium, which belongs to the boundary of Ω. Other equilibrium points must be found from the system of equations

\begin{equation} \label{EqTumor.2} s + c\,T - \beta\, E\cdot T - E = 0, \quad 1 - T - \frac{\alpha \, E}{1 + \varepsilon\, T} = 0 . \end{equation}
From the first equation follows that \( \displaystyle E = \frac{s + c\,T}{1 + \beta\,T} . \) Substitution into the second one gives
\begin{equation} \label{EqTumor.3} 1 - T - \frac{\alpha \left( s + c\,T \right)}{\left( 1 + \varepsilon T \right)\left( 1 + \beta\,T \right)} = 0 . \end{equation}
Upon introducing function
\[ f(T) = 1 - \frac{\alpha \left( s + c\,T \right)}{\left( 1 + \varepsilon T \right)\left( 1 + \beta\,T \right)} , \]
we can rewrite Eq.\eqref{EqTumor.3} as
\[ f(T) = T . \]

Equilibrium point.
     
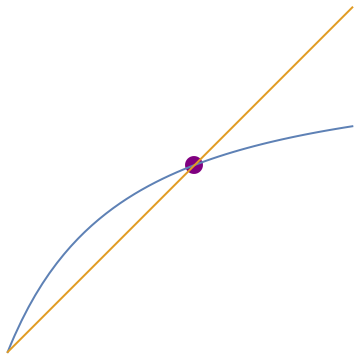
f[t_] = 1 - (1 + 0.5*t)/(1 + t)/(1 + 2*t);
plot=Plot[{f[t], t}, {t, 0, 1.2}, PlotStyle -> Thick];
point = Graphics[{PointSize[0.05], Purple, Point[{0.651, 0.651}]}]; Show[point, plot]
NSolve[f[t] == t, t]
{{t -> -1.15139}, {t -> 0.651388}, {t -> 0.}}

 

  1. Kirschner, D., Panetta, J.C., Modeling immunotherapy of the tumor-immune interaction, Journal of Mathematical biology, 1998, 37, pp. 235--252.
  2. Kuznetsov, V.A., Makalkin, I.A., Taylor, M.A., Perelson, A.S., Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis, Journal of Mathematical biology, 1994, 56, pp. 295--321.
  3. Li, J., Xie, X., Chen, Y., Zhang, D., Complex dynamics of a tumor-immune system with antigenicity, Applied Mathematics and Computation, 2021, 400, 126052.

 

  2. Bjørnstad, O.N., Shea, K., Krzywinski, M., The SEIRS model for infectious disease dynamics, Nature Methods, 2020, volume 17, pages 557–558. https://doi.org/10.1038/s41592-020-0856-2
  3. SIR and SIRS Models, IDM
  4. Smith, D. and Moore, L., The SIR Model for Spread of Disease - The Differential Equation Model, The American Mathematical Monthly,
  5. Yano, T.K., Makinde, O.D., Malonza, D.M., Modelling Childhood Disease Outbreak in a Community with Inflow of Susceptible and Vaccinated New-born, Global Journal of Pure and Applied Mathematics, 2016, Volume 12, Number 5, pp. 3895-3916.

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions