Preface

This section presents the famous van der Pol equation

Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part VI of the course APMA0340
Introduction to Linear Algebra

Glossary

van der Pol Equations

Balthasar van der Pol

  The van der Pol oscillator is a non-conservative oscillator that is modeled by the following differential equation

\begin{equation} \label{EqPol.1} \frac{{\text d}^2 x}{{\text d} t^2} - \mu \left( 1 - x^2 \right) \frac{{\text d}x}{{\text d} t} + x =0 \qquad \mbox{or} \qquad \ddot{x} - \mu \left( 1 - x^2 \right) \dot{x} + x =0 , \end{equation}
where x is the position coordinate---which is a function of the time t, and μ is a scalar parameter indicating the nonlinearity and the strength of the damping. This unforced differential equation was first introduced by Lord Rayleigh in 1883 to model the oscillations of a clarinet reed. However, the Dutch electrical engineer and physicist Balthasar van der Pol (1889--1959), who was known as Balth, was the first to initiate modern experimental and theoretical dynamics in the laboratory during the 1920s and 1930s. Balth was the first who used the above model in his research. He investigated electrical circuits by employing vacuum tubes and found that they have stable oscillations, now called limit cycles. He was awarded the Institute of Radio Engineers (now the IEEE) Medal of Honor in 1935. The asteroid 10443 van der Pol was named after him. Van der Pol built a number of electronic circuit models of the human heart to study the range of stability of heart dynamics. His investigations with adding an external driving signal were analogous to the situation in which a real heart is driven by a pacemaker.

In the September 1927 issue of the British journal Nature, Van der Pol and his colleague J. van der Mark published an article entitled "Frequency Demultiplication" in which they reported an "irregular noise" before transition from one subharmonical regime to another one. By reconstructing his electronic tube circuit, we now know that they had discovered deterministic chaos. Their paper is probably one of the first experimental reports of chaos. In particular, they considered the forced oscillations of a triode, but in the field of relaxation oscillations:

\[ \ddot{v} - \alpha \left( 1- v^2 \right) + \omega_0^2 v = \omega_1^2 E\,\sin \left( n \omega_1 t \right) \qquad\mbox{with} \quad \varepsilon = \frac{\alpha}{\omega_0} \gg 1 . \]
They showed that for n = 3, the above forced van der Pol equation admits an exact solution \( v(t) = 2\,\cos \left( \omega_0 t \right) \) for E = 2ε. It therefore appears that the frequency of this solution is three times the forcing one.

During the 1930s, Russian mathematicians Nikolai M. Krylov (1879--1955) and Nikolai N. Bogolyubov (1909--1992), inscribed the slowly varying amplitudes method unveiled a few years earlier by van der Pol in the framework of a theory that now bares their names. The Krylov--Bogolyubov averaging method is based on the averaging principle when the exact differential equation of the motion is replaced by its averaged version. Their work attracted quite a bit of attention with full support of the famous French mathematician Jacques Hadamard (1865--1963). They put mathematical foundation into van der Pol experimental research.

Between 1931 and 1933. many articles were published in Russian on the study of resonance and frequency demultiplication phenomena by a group of scientists, including Leonid Mandelshtam, Nikolai Papalexi, Alexandr Andronov, Semen Khaikin, and Alexander Witt. They analyzed the stability of periodic solutions based on Poincaré--Lindstedt method.

In 1945, M.L. Cartwright and J.E. Litlewood published the article where they showed that the van der Pol equation admits singular solutions for large values of parameter μ. Later in 1949, N. Levinson analytically analyzing the van der Pol equation confirms that it has singular solutions. On the basis of numerical simulations, it was observed that the transition from periodic oscillations to chaotic ones is possible. Further history of analyzing van der Pol oscillator could be found in the article by Ginoux and Letellier.

To analyze stability of solutions to van der Pol equation, we rewrite his second order differential equation

\[ \ddot{x} + x = \mu \left( 1 - x^2 \right) \dot{x} \]
in equivalent form of system of first order equations

\begin{equation} \label{EqPol.2} \begin{split} \dot{\bf x} &= v , \\ \dot{\bf v} &= -x - \mu \left( x^2 -1 \right) v . \end{split} \end{equation}
Upon equating slope functions to zero, we see that the system has one critical point---the origin. Now we choose a Lyapunov function in the form
\[ V(x,v) = x^2 + v^2 \qquad\Longrightarrow \qquad \dot{V} = 2\mu \dot{v}^2 \left( 1- x^2 \right) . \]
If μ is positive, then the derivative of V with respect to the van der Pol equation is also positive for |x| < 1, so the origin is unstable. This happens because energy is added to the system when the displacement is small, i.e. |x| < 1. The Lyapunov theorem guarantees that every trajectory starting inside the unit circle tends to a closed loop.

On the other hand, when x is large, the cubic term x3 becomes dominant and the damping becomes positive. In this case, \( \dot{V}(x,y) \le 0 . \) Energy is dissipated for large displacement corresponding to |x| > 1. Therefore, the system is expected to be restricted in some area around the fixed point and the system approaches a limit cycle. Using the Liénard's transformation \( y = x - x^3 / - \dot{x} /\epsilon , \) the van der Pol equation can be rewritten as

\[ \begin{split} \dot{x} &= \mu \left( x - \frac{1}{3}\, x^3 - y \right) , \\ \dot{y} &= x/\mu , \end{split} \]
which can be considered as the FitzHugh--Nagumo model, also known as the Bonhoeffer--van der Pol oscillator.
Flows of the van der Pol oscillator for small μ
Flows of the van der Pol oscillator for large μ

Actually, the van der Pol equation is a particular case of more general Liénard equation:

\[ \ddot{x} + f(x) \,\dot{x} + g(x) =0 , \]
named after the French physicist Alfred-Marie Liénard (1869--1958). The Van der Pol equation has no exact, analytic solution, but it has a limit cycle.
Theorem 1: There is one nontrivial periodic solution of the van der Pol equation and every other solution (except the equilibrium point at the origin) tends to this periodic solution.
Example 1: In order to obtain information regarding the approach to the limit cycle, we use a powerful perturbation method called the method of averaging. We begin with a system of the more general form:
\[ \ddot{x} + x = \mu \,f \left( x,\dot{x} \right) , \]
where in our case
\[ f \left( x,\dot{x} \right) = \left( 1 - x^2 \right) \dot{x} . \]
We seek its solution in the form:
\[ \begin{split} x &= a(t)\,\cos \left( t + \psi (t) \right) , \\ \dot{x} &= -a(t) \,\sin \left( t + \psi (t) \right) . \end{split} \]
Our motivation for this ansatz is that when µ is zero, the van der Pol equation has its solution of the above form with a and ψ constants. For small values of µ we expect the same form of the solution to be approximately valid, but now a and ψ are expected to be slowly varying functions of t. Differentiating equations for x and its derivative, we obtain the relation for unknown parameters a and ψ:
\[ \frac{{\text d}a}{{\text d}t} \,\cos \left( t + \psi (t) \right) -a\,\frac{{\text d}\psi}{{\text d}t} \,\sin \left( t + \psi (t) \right) =0. \]
Next differentiation of the velocity and using van der Pol equation, we come to
\[ -\frac{{\text d}a}{{\text d}t} \,\sin \left( t + \psi (t) \right) - a\,\frac{{\text d}\psi}{{\text d}t} \,\cos \left( t + \psi (t) \right) = \mu f \left( a(t)\,\cos \left( t + \psi \right) - a(t)\, \sin \cos \left( t + \psi \right) \right) . \]
Solving the above equation for \( \dot{a} \quad\mbox{and}\quad \dot{\psi} , \) we obtain
\[ \begin{split} \frac{{\text d}a}{{\text d}t} &= -\mu \,f \left( a(t)\,\cos (t+\psi ) , -a(t)\,\sin (t+\psi ) \right) \sin (t+\psi ) , \\ \frac{{\text d}\psi}{{\text d}t} &= -\frac{\mu}{a} \,f \left( a(t)\,\cos (t+\psi ) , -a(t)\,\sin (t+\psi ) \right) \sin (t+\psi ) , \end{split} \]
where
\[ \begin{split} f (\ldots , \ldots ) &= a\left( a^2 \cos^2 (t+\psi ) -1 \right) \sin (t+\psi ) , \\ \dot{a} &= -\mu \,a \left( a^2 \cos^2 (t+\psi ) -1 \right) \sin^2 (t+\psi ) , \\ \dot{\psi} &= -\mu \left( a^2 \cos^2 (t+\psi ) -1 \right) \sin (t+\psi ) \, \cos (t+\psi ) . \end{split} \]
So far our treatment has been exact and is essentially the procedure of variation of parameters which is used to obtain particular solutions to nonhomogenous linear differential equations. Now we introduce the following approximation: since µ is small, \( \dot{a} \quad\mbox{and}\quad \dot{\psi} , \) are also small. Hence a(t) and ψ(t) are slowly varying functions of t. Thus over one cycle of oscillations the quantities a(t) and ψ(t) on the right hand sides of the latter can be treated as nearly constant, and thus these right hand sides may be replaced by their averages:
\[ \frac{1}{2\pi} \,\int_0^{2\pi} {\text d} \phi \ldots . \]
This yields
\[ \begin{split} \dot{a} &= -\frac{\mu}{2\pi} \,\int_0^{2\pi} {\text d}\phi \,a \left( a^2 \cos^2 (t+\phi ) -1 \right) \sin^2 ( \phi ) , \\ \dot{\psi} &= -\frac{\mu}{2\pi} \,\int_0^{2\pi} {\text d}\phi \left( \cos^2 (t+\phi ) -1 \right) \sin ( \phi ) \,\cos ( \phi ) . \end{split} \]
The right hand side of the latter is zero. The averaging in the previous equation for \( \dot{\psi} \) can be done using the following trigonometric identities:
\[ \cos^2 (\phi ) = \frac{1}{2} \left[ 1 + \cos (2\phi ) \right] , \qquad \sin^2 (\phi ) = \frac{1}{2} \left[ 1 - \cos (2\phi ) \right] . \]
This leads to
\[ \begin{split} \int_0^{2\pi} {\text d}\phi \,\cos^2 \left( n \phi \right) &= \int_0^{2\pi} {\text d}\phi \,\sin^2 \left( n \phi \right) = \pi , \qquad n=1,2,\ldots , \\ \int_0^{2\pi} {\text d}\phi \,\cos \left( n \phi \right) &= \int_0^{2\pi} {\text d}\phi \,\sin \left( n \phi \right) = 0 , \qquad n=1,2,\ldots , \\ \int_0^{2\pi} {\text d}\phi \,\cos^4 \left( \phi \right) &= \frac{3}{4}\, \pi , \\ \int_0^{2\pi} {\text d}\phi \,a \left( a^2 \cos^2 (\phi ) -1 \right) \sin^2 (\phi ) \frac{\pi}{4} \, a \left( a^2 -4 \right) . \end{split} \]
So
\[ \dot{a} = \frac{\mu}{8} \,a \left( 4 - a^2 \right) . \]
The latter is a separable equation, which we integrate directly to obtain
\[ \ln \left( \frac{a+2}{a^2 (2-a)} \right) = \mu \left( t + t_0 \right) . \]
Therefore,
\[ a(t) \approx 2 - e^{-\mu \,t} . \]
■

Our next step in analyzing the trajectories of the van der Pol equation is to linearize the corresponding system of first order equations. Although Mathematica has a dedicated command JacobianMatrix, we calculate it directly. First, we build a matrix of its slope functions.

vdot[t_] = mu (1 - x[t]^2)*x'[t] - x[t]
Out[1]= -x[t] + mu (1 - x[t]^2) Derivative[1][x][t]
M = {{0, 1}, {D[vdot[t], x[t]], D[vdot[t], x'[t]]}}
Out[2]= {{0, 1}, {-1 - 2 mu x[t] Derivative[1][x][t], mu (1 - x[t]^2)}}
MO = M /. {x[t] -> 0, x'[t] -> 0}
Out[3]= {{0, 1}, {-1, mu}}
So the Jacobian matrix is
MO // MatrixForm
Out[4]= \( \begin{pmatrix} 0&1 \\ -1& \mu \end{pmatrix} \)
Since the Jacobian matrix has two eigenvalues with positive real part, the origin is unstable stationary point.
Eigenvalues[MO]
Out[3]= {1/2 (mu - Sqrt[-4 + mu^2]), 1/2 (mu + Sqrt[-4 + mu^2])}
The following example demonstrates a series of Mathematica codes for solving numerically the van der Pol equation. Note for numerical procedure NDSolve it does not matter whether the equation is homogeneous or driven.
Example 2: We start with a particular numerical value of parameter μ = 0.5. the initial conditions are chosen very close to zero.

     
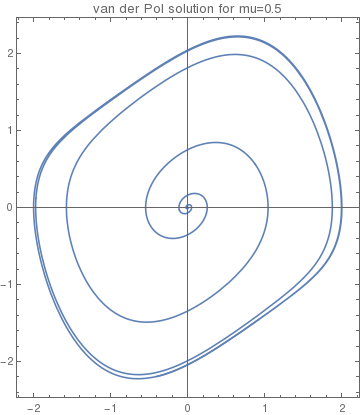
vdot[t_] = mu (1 - x[t]^2)*x'[t] - x[t]
vdot05[t_] = vdot[t] /. mu -> 0.5
Out[6]= -x[t] + 0.5 (1 - x[t]^2) Derivative[1][x][t]
Orbit1 = NDSolve[{v'[t] == vdot05[t], x'[t] == v[t], x[0] == 0.01,  v[0] == 0}, {x, v}, {t, 0, 40}]
Out[7]= {{x->InterpolatingFunction[{0.,40.}},<>],
v->InterpolatingFunction[{0.,40.}},<>]}}

plot05 = ParametricPlot[{x[t] /. Orbit1[[1]],
v[t] /. Orbit1[[1]]}, {t, 0, 40}, Frame -> True,
PlotLabel -> "van der Pol solution for mu =0.5"]
       A solution of the van der Pol equation \eqref{EqPol.1}.            Mathematica code

 

 Then we take another initial condition far away from the origin.

     
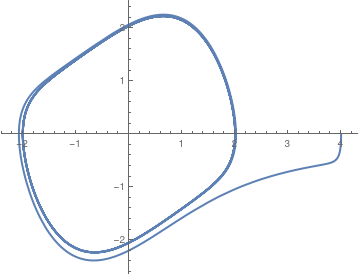
vdot[t_] = 0.5 (1 - x[t]^2)*v[t] - x[t]
Orbit2 = NDSolve[{v'[t] == 0.5 (1 - x[t]^2)*v[t] - x[t], x'[t] == v[t], x[0] == 4.0, v[0] == 0}, {x, v}, {t, 0, 40}];
plot054 = ParametricPlot[{x[t] /. Orbit2[[1]], v[t] /. Orbit2[[1]]}, {t, 0, 40}, PlotStyle -> Thick]
       Another solution to the van der Pol equation \eqref{EqPol.1}.            Mathematica code

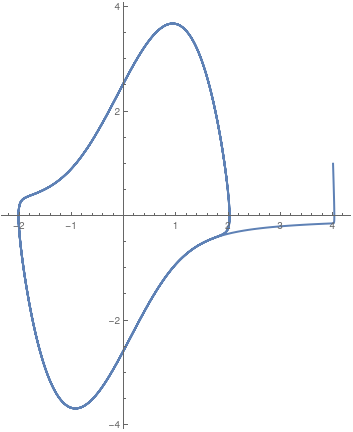
      Now we plot a solution curve when parameter μ is larger than 1,
vdot[t_] = 1.89 (1 - x[t]^2)*v[t] - x[t]
Orbit2 = NDSolve[{v'[t] == 0.5 (1 - x[t]^2)*v[t] - x[t], x'[t] == v[t], x[0] == 4.0, v[0] == 1.0}, {x, v}, {t, 0, 40}];
plot054 = ParametricPlot[{x[t] /. Orbit2[[1]], v[t] /. Orbit2[[1]]}, {t, 0, 40}, PlotStyle -> Thick]
       A solution curve to the van der Pol equation \eqref{EqPol.1} when μ = 1.89.            Mathematica code

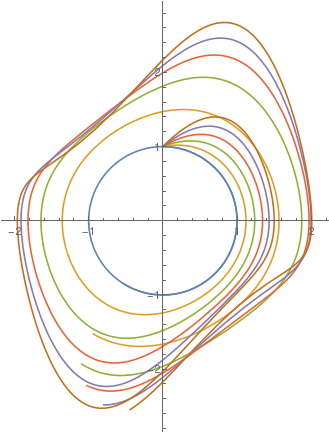
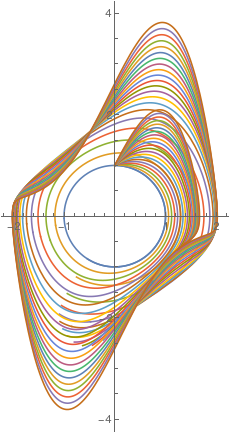
      Upon changing the value of parameter μ, we plot solutions to the van der Pol equation \eqref{EqPol.1}, starting with μ = 0 (the limit cycle has the form of pure circle), with step size 0.2 untill μ = 1.
sol[mu_?NumericQ] := First@NDSolve[{y''[t] - mu*(1 - y[t]^2) y'[t] + y[t] == 0, y[0] == 0, y'[0] == 1}, y, {t, 0, 10}]
ParametricPlot[Evaluate[{y[t], y'[t]} /. sol[#] & /@ Range[0, 1, 0.2]], {t, 0, 10}]
       A family of solutions to the van der Pol equation for different values of parameter μ.            Mathematica code

      You can also use ParametricNDSolve:
sol = ParametricNDSolveValue[{y''[t] - mu*(1 - y[t]^2) y'[t] + y[t] == 0, y[0] == 0, y'[0] == 1}, y, {t, 0, 10}, {mu}];
ParametricPlot[Evaluate[{sol[#][t], D[sol[#][t], t]} & /@ Range[0, 2, 0.1]], {t, 0, 10}]
The figure shows the change in graphs when parameter μ changes within the range [0, 2].
       A family of solutions to the van der Pol equation for different values of parameter μ.            Mathematica code

 

Now we pick up a large value for parameter μ:

vdot3[t_] = vdot[t] /. mu -> 3.0
Orbit3 = NDSolve[{v'[t] == vdot3[t], x'[t] == v[t], x[0] == 0.01, v[0] == 0}, {x, v}, {t, 0, 40}]
ParametricPlot[{x[t] /. Orbit3[[1]], v[t] /. Orbit3[[1]]}, {t, 0,
40}, Frame -> True, AspectRatio -> 1.0, PlotRange -> 5.1, PlotLabel -> "van der Pol solution for mu =3"]
Similarly, we take another initial conditions
Orbit33 =
NDSolve[{v'[t] == vdot3[t], x'[t] == v[t], x[0] == 3.0,
v[0] == 0}, {x, v}, {t, 0, 40}]
plot33 = ParametricPlot[{x[t] /. Orbit33[[1]],
v[t] /. Orbit33[[1]]}, {t, 0, 40}, Frame -> True,
AspectRatio -> 1.0, PlotRange -> 5.1,
PlotLabel -> "van der Pol solution for mu =3"]
ParametricPlot[
Evaluate[Table[{x[t], x'[t]} /.
NDSolve[{x''[t] - 3 (1 - (x[t])^2) x'[t] + x[t] == 0, x[0] == c,
x'[0] == 0}, {x[t], x'[t]}, {t, 0, 50}], {c, -1, 1, 0.1}]], {t,
0, 50}, PlotRange -> {{-3, 3}, {-5.1, 5.1}}, PlotStyle -> Purple]
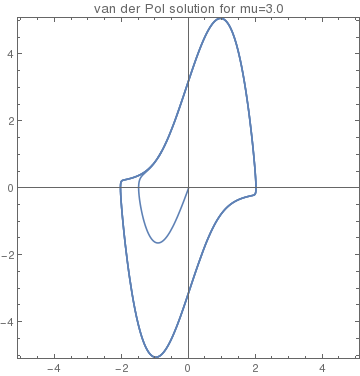
Solutions of van der Pol equation for
initial conditions inside the unit circle
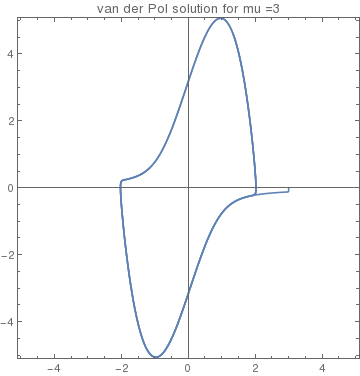
Solutions of van der Pol equation for
initial conditions outside the unit circle

 

Plot with colors (Orlando):

Show[Table[
ParametricPlot[
Evaluate[{x[t], x'[t]} /.
NDSolve[{x''[t] - 3 (1 - (x[t])^2) x'[t] + x[t] == 0, x[0] == c,
x'[0] == 0}, {x[t], x'[t]}, {t, 0, 50}]], {t, 0, 50},
PlotRange -> {{-3, 3}, {-5.1, 5.1}},
PlotStyle -> Hue[(c + 1)/2]], {c, -1, 1, 0.1}]]

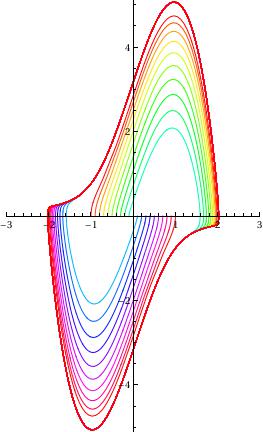
with two colors:

black = ParametricPlot[
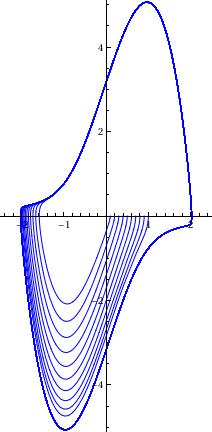
Evaluate[Table[{x[t], x'[t]} /.
NDSolve[{x''[t] - 3 (1 - (x[t])^2) x'[t] + x[t] == 0, x[0] == c,
x'[0] == 0}, {x[t], x'[t]}, {t, 0, 50}], {c, -1, 0, 0.1}]], {t,
0, 50}, PlotRange -> {{-2.5, 2.5}, {-5.1, 5.1}},
PlotStyle -> Black]

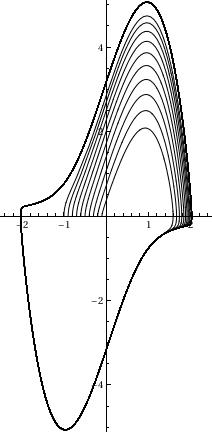
blue = ParametricPlot[
Evaluate[Table[{x[t], x'[t]} /.
NDSolve[{x''[t] - 3 (1 - (x[t])^2) x'[t] + x[t] == 0, x[0] == c,
x'[0] == 0}, {x[t], x'[t]}, {t, 0, 50}], {c, 0, 1, 0.1}]], {t,
0, 50}, PlotRange -> {{-2.5, 2.5}, {-5.1, 5.1}}, PlotStyle -> Blue]

Show[black, blue]

 

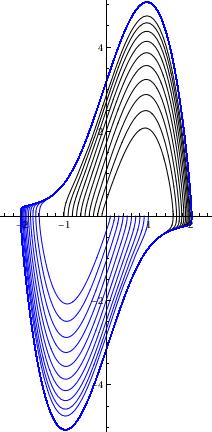
With direction field:

field = VectorPlot[{y, 1*(1 - x^2)*y - x}, {x, -4.2, 4.2}, {y, -6.5, 6.5}, VectorScale -> {Small, 1}]

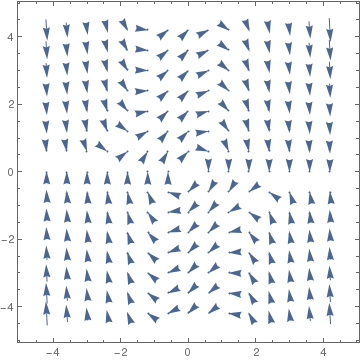
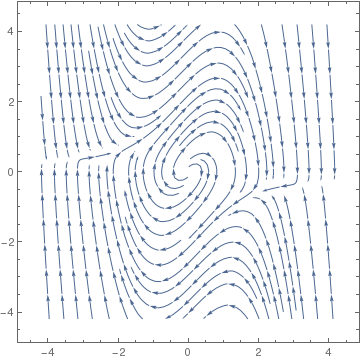
Instead of Vectorplot, sometimes StreamPlot presents the phase portrait better:

StreamPlot[{y, 1*(1 - x^2)*y - x}, {x, -4.2, 4.2}, {y, -4.2, 4.2}, VectorScale -> {Small, 1}]

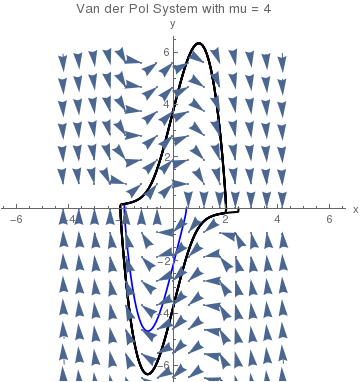
We plot solutions and vector field together.
de1 = x'[t] == y[t];
de2 = y'[t] == 4*(1 - (x[t])^2)*y[t] - x[t];
soln1 = NDSolve[{de1, de2, x[0] == 0.5, y[0] == 0}, {x, y}, {t, 0, 40}]
soln2 = NDSolve[{de1, de2, x[0] == 2.5, y[0] == 0}, {x, y}, {t, 0, 40}]
plot1 = ParametricPlot[Evaluate[{x[t], y[t]} /. soln1], {t, 0, 40},
PlotStyle -> {RGBColor[0, 0, 1], Thickness[0.005]}, DisplayFunction -> Identity, PlotRange -> 6.6]
plot2 = ParametricPlot[Evaluate[{x[t], y[t]} /. soln2], {t, 0, 40},
PlotStyle -> {Black, Thickness[0.006]}, DisplayFunction -> Identity]
Show[plot1, plot2, field, PlotLabel -> "Van der Pol System with mu = 4",
AxesLabel -> {"x", "y"}, DisplayFunction -> $DisplayFunction]

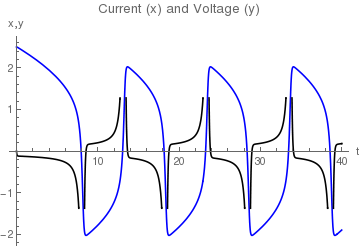
Kplot = Plot[Evaluate[x[t] /. soln2[[1]][[1]]], {t, 0, 40},
PlotStyle -> RGBColor[0, 0, 1], DisplayFunction -> Identity]

Vplot = Plot[Evaluate[y[t] /. soln2[[1]][[2]]], {t, 0, 40},
PlotStyle -> Black, DisplayFunction -> Identity]

Show[Kplot, Vplot, PlotLabel -> "Current (x) and Voltage (y)",
AxesLabel -> {"t", "x,y"}, DisplayFunction -> $DisplayFunction]

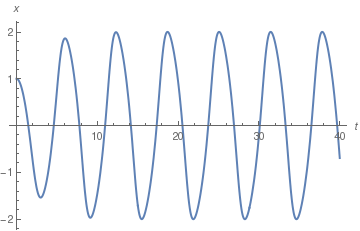
If you want to determine just one variable x, you don't need to transfer van der Pol equation to the system; Mathematica allows you to find it.

vanderpol[mu_] := NDSolve[{x''[t] + mu*(x[t]^2 -1)*x'[t] + x[t] ==0, x[0] == 1, x'[0] ==0}, x[t], {t,0,40}]
For example, entering
numsol05 = vanderpol[0.5]
Plot[x[t]/.numsol05, {t,0,40}, PlotStyle->Thick, AxesLabel->{t,x}]
returns a numerical solution to the initial value problem for van der Pol equation with μ = 0.5 and then graphs the result on the interval [0,40]:
Entering
numsol05/.t->3.7
{{x[3.7] -> -1.21224}}
provides the numerical value at t = 3.7. You can also plot the derivative of the numerical solution on the interval [0,40].
Plot[Evaluate[D[numsol05[[1,1,2]],t]], {t,0,40}]

Now we define a subroutine solgraph that depends on two parameters: μ and opts (which is shortcut for option in Plot command).

solgraph[mu_,opts___] := Module[{numsol1}, numsol1 = vanderpol[mu]; Plot[x[t]/.numsol1, {t,0,40}, opts, PlotRange -> {-3,3}, Ticks -> {{0,40},{-3,3}}, DisplayFunction -> Identity]]
For instance, entering
solgraph[3.5, DisplayFunction -> $DisplayFunction]
displays the graph of the solution to the van der Pol equation with μ = 0.5 on the interval [0,40]. We can change the value of μ by entering
muvals = {1/20,1/15,1/10, 1/5,1/2,1,2,2.3,4,7,9}
the list of numerical values of μ that we would like to calculate. So we plug in
graphs = Map[solgraph,muvals]
Here is another version of the code:
process[mu_]:=Module[
{sol,p1,p2,p3,data,system,z,x1, x2,t,ode1,ode2,timeScale},
ode1 =x1'[t]==x2[t];
ode2 =x2'[t]==z(1-x1[t]^2)x2[t]-x1[t];
timeScale ={t,0,80};
sol=First@NDSolve[ {ode1,ode2/.z->mu,x1[0]==0.01,x2[0]==0},
{x1[t],x2[t]},
timeScale,Method->{"Extrapolation", Method->"LinearlyImplicitEuler"}];
sol = {x1[t],x2[t]}/.sol;
p1 = Plot[Evaluate[sol[[1]]],
Evaluate[timeScale], Frame->True, FrameLabel->{"time","y(t)"}, PlotLabel->"\[Mu]="<>ToString[mu]];
p2 = Plot[Evaluate[sol[[2]]], Evaluate[timeScale],
Frame->True, FrameLabel->{"time","y'(t)"}, PlotLabel->"\[Mu]="<>ToString[mu], PlotStyle->RGBColor[1,0,0]];
data = Table[{Evaluate[sol[[1]]], Evaluate[sol[[2]]]}, Evaluate[timeScale]];
p3=ListPlot[data,Joined->True,Frame->True,
PlotLabel->"\[Mu]="<>ToString[mu], FrameLabel->{"y(t)","y'(t)"}, PlotRange->All];
{p1,p2,p3}
];
mu={0.1,.2,1,3,5,10};
r = process/@mu; Grid[r]
■

It is right time to mention some generalizations of the van der Pol equation. For instance, the following one:

\[ \ddot{x} + 2\beta \left( 1 - \alpha x^2 + \gamma x^4 \right) \dot{x} + x =0 . \]
Example 3: Chaos synchronization has received increasing attention as an interesting phe- nomenon of practical importance in coupled chaotic oscillators, due to its theoretical challenge and its great potential applications in secure communication, chemical reaction, biological systems and so on. Various types of synchronization have been studied.

One particular characteristic in the van der Pol model is that its phase depends on initial conditions. Therefore, if two van der Pol oscillators run with different initial conditions, their trajectory will finally circulate on the same limit cycle with different phases φ1 and φ2. The chaos synchronization problem can be formulated as follows: Given a chaotic system, which is considered as the master (or driving) system, and another identical system, which is considered as the slave (or response) system, the aim is to force the response of the slave system to synchronize the master system in such a way that the dynamical behaviors of these two systems be identical after a transient time.

■

Liénard's theorem can be used to prove that the system has a limit cycle. Applying the Liénard transformation \( y = x - x^3 / 3 - \dot{x}/\mu , \) where the dot indicates the time derivative, the Van der Pol oscillator can be written in its two-dimensional form:

\[ \begin{split} \dot{x} &= \mu \left( x - \frac{1}{3}\, x^3 -y \right) , \\ \dot{y} & = x/\mu . \end{split} \]

 

Driven van der Pol Equations

The forced, or driven, Van der Pol oscillator takes the 'original' function and adds a driving function Asin(ωt) to give a differential equation of the form:
\[ \ddot{x} -\mu \left( 1 - x^2 \right) \dot{x} +x = A\, \sin (\omega t), \]
where A is the amplitude, or displacement, of the wave function and ω is its angular velocity. We repeat calculations for nonhomogeneous van der Pol equation \( \ddot{x} - 0.5 \left( 1 - x^2 \right) \dot{x} + x = \sin (\pi t) : \)
Orbit22 = NDSolve[{v'[t] == vdot05[t] + Sin[Pi*t], x'[t] == v[t], x[0] == 4.0, v[0] == 0}, {x, v}, {t, 0, 40}];
plot22 = ParametricPlot[{x[t] /. Orbit22[[1]], v[t] /. Orbit2[[1]]}, {t, 0, 40}]
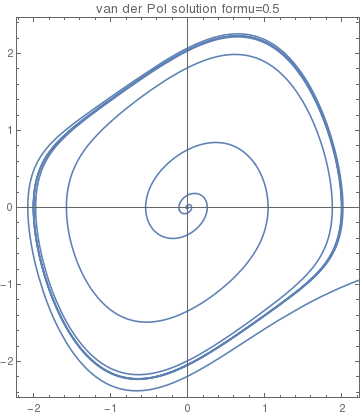
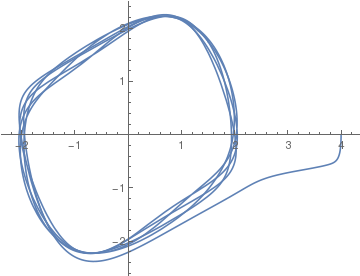
Solutions of homogeneous van der Pol equation
Solutions of nonhomoheneous van der Pol equation

Upon introducing new parameter ε = 1/μ², we convert the forced van der Pol equation to autonoumous system of equations:

\[ \begin{split} \epsilon\,\dot{x} &= y + x - x^3 /3 , \\ \dot{y} &= -x + A\,\sin \left( \omega \theta \right) , \\ \dot{\theta} &= \omega , \end{split} \]
where θ = ωt, \( y = \dot{x}/\mu^2 + x^3 /3 -x . \)

 

Chaos

If a forcing term F sin(ωdt) or F cos(ωdt) is added to the right-hand side of Eq.\eqref{EqPol.1}, then the solutions may, for certain values of α, be chaotic. That is, solutions may show sensitive dependence on initial conditions, making the precise behavior of the oscillator effectively unpredictable, even though it is governed by a deterministic equation.

During their experiments with frequency demultiplication in electrical circuits, van der Pol and van der Mark were the first to observe the onset of chaos in a simple nonlinear system. At the time, however, they did not fully appreciate the significance of this phenomenon. Inspired by van der Pol’s work, Mary Cartwright and J. E. Littlewood proceeded to investigate the problem mathematically. For a modern review of this subject, see J. M. T. Thompson and H. B. Stewart.

 

Hamiltonian for van der Pol Equations

One can also write a time-independent Hamiltonian formalism for the Van der Pol oscillator by augmenting it to a four-dimensional autonomous dynamical system using an auxiliary second-order nonlinear differential equation as follows:
\[ \begin{split} \ddot{x} -\mu \left( 1 - x^2 \right) \dot{x} +x = 0, \\ \ddot{y} -\mu \left( 1 - x^2 \right) \dot{y} +y = 0. \end{split} \]
Note that the dynamics of the original Van der Pol oscillator is not affected due to the one-way coupling between the time-evolutions of x and y variables. A Hamiltonian H for this system of equations can be shown to be
\[ H \left( x, y, p_x , p_y \right) = p_x p_y + x\,y - \mu \left( 1 - x^2 \right) y\, p_y , \]
where \( p_x = \dot{y} + \mu \left( 1 - x^2 \right) y \) and \( p_y = \dot{x} \) are the conjugate momenta corresponding to x and y, respectively.

 

  1. Adelakun, A.O., Njah, A.N., Olusola, O.I. and Wars, S.T., Computer and Hardware Modeling of Periodically Forced -Van der Pol Oscillator, Active and Passive Electronic Components Volume 2016, Article ID 3426713, 7 pages http://dx.doi.org/10.1155/2016/3426713.
  2. Albarakati, W.A., Lloyd, N.G. & Pearson, J.M., Transformation to Liénard form, Electronic Journal of Differential Equations, Vol. 2000 (2000), No. 76, pp. 1--11.
  3. Cartwright, M.L. and Litlewood, J.E., "On Non‐Linear Differential Equations of the Second Order: I. the Equation \( y'' - k (1 - y^2) y' +y = b\lambda k\,\cos (\lambda t + \alpha ), \) k large", Journal of the London Mathematical Society, 20, Issue 3, pp. 180--189, 1945; https://doi.org/10.1112/jlms/s1-20.3.180
  4. G. Chen and X. Dong, From Chaos to Order: Methodologies, Perspectives and Applications, World Scientific, Singapore, 1998.
  5. Cooper, M, Heidlauf, P. and Sands, T., Controlling Chaos—Forced van der Pol Equation.
  6. D’Acunto, M., Determination of limit cycles for a modified van der Pol oscillator, Mechanics Research Communications, 2006, Vol. 33, No. 1, pp. 93--98; doi: 10.1016/j.mechrescom.2005.06.012
  7. Dadfar, M.B. and Geer, J..F., Resonances and Power Series Solutions of the Forced Van Der Pol Oscillator, SIAM Journal of Applied Mathematics, Vol. 50, No. 5, pp. 1496--1506, 1990.
  8. Gh. Asadi Cordshooli and Vahidi, A.R., Phase synchronization of van der Pol--Duffing oscillators using decomposition method, Advanced Studies in Theoretical Physics, Vol. 3, No. 11, pp. 429--437.
  9. Ginoux, J.-M., and Letellier, C., Van der Pol and the history of relaxation oscillations: toward the emergence of a concept, 2012.
  10. Gleick, James, Chaos: Making a New Science 1987.
  11. Guckenheimer, J., Hoffman, K. and Weckesser, W., The Forced van der Pol Equation I: The Slow Flow and Its Bifurcations, SIAM Journal of Applied Dynamic Systems, 2003 Society for Industrial and Applied Mathematics Vol. 2, No. 1, pp. 1–35.
  12. Guckenheimer, J., Hoffman, K. and Weckesser, W., The Forced van der Pol Equation II: anards in the Reduced System , SIAM Journal of Applied Dynamic Systems, 2003 Society for Industrial and Applied Mathematics Vol. 2, No. 4, pp. 570--608.
  13. Holmes, P.J. and Rand, D.A., Bifurcation of the forced van der Pol oscillator, Quarterly of Applied Mathematics, 1978, No. 1, pp. 495--509.
  14. Janson, N.B., Balanov, A.G., Anishchenko, V.S., and McClintock, P.V.E., Phase relationships between two or more interacting processes from one-dimensional time series. I. Basic theory, Physical Review, E, Vol. 65, 036211 2002, doi: https://doi.org/10.1103/PhysRevE.65.036211
  15. Janson, N.B., Balanov, A.G., Anishchenko, V.S., and McClintock, P.V.E., Phase relationships between two or more interacting processes from one-dimensional time series. II. Application to heart-rate-variability data, Physical Review, E, Vol. 65, 036212 (2002)
  16. Levinson, N., A Second Order Differential Equation with Singular Solutions Norman Levinson, Annals of Mathematics, Second Series, Vol. 50, No. 1 (Jan., 1949), pp. 127-153 (27 pages).
  17. Kovacic, I. and Mickens, R.E., A generalized van der Pol type oscillator: Investigation of the properties of its limit cycle, Mathematical and Computer Modelling Volume 55, Issues 3–4, February 2012, Pages 645--653, https://doi.org/10.1016/j.mcm.2011.08.038
  18. Pinto, Carla and Machado, T., Complex-order forced van der Pol oscillator, Journal of Vibration and Control, 18(14) 2201–2209, 2011. doi: 0.1177/1077546311429150
  19. Semenova, N.I. and Anishchenko V.S., Fibonacci stairs and the Afraimovich-Pesin dimension for a stroboscopic section of a nonautonomous van der Pol oscillator, Chaos, Vol. 25, Issue 7, 073111 (2015); https://doi.org/10.1063/1.4926453
  20. Soomro, A.S., Tularam, G.A., Shaikh, M.M., A Comparison of Numerical Methods for Solving the Unforced Van Der Pol’s Equation, Mathematical Theory and Modeling, 2013, Vol. 3, No. 2.
  21. J. M. T. Thompson and H. B. Stewart, Nonlinear Dynamics and Chaos, 2nd ed., (Chichester: John Wiley & Sons, 2002).
  22. Tsatsos, Marios, Theoretical and Numerical Study of the van der Pol equation. 2006.
  23. Van der Pol, B. and Van der Mark, J., Frequency demultiplication, Nature, 120, Number 3019, 1927, pp. 363--364.
  24. Van der Pol oscillator
  25. van der Pol oscillator Scholarpedia.
  26. Xu, J.-X. and Jiang, J., The Global Bifurcation Characteristics of the Forced van der Pol oscillator, Chaos, Solitons, and Fracrals, Vol. 7. No. 1. pp 3--19. 1996.

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions