Preface
Not every solution to the Duffing equation is bounded---it depends on the initial conditions and pareametrers of the input periodic function.
Forced anharmonic motion
Our main concern is the existence of bounded solutions to the forced Duffing equation
Dependence on initial conditions

|
pfun = ParametricNDSolveValue[{x''[t] == -x[t] + x[t]^3/6 +
0.3*Cos[0.5*t], x[0] == a, x'[0] == b}, x, {t, 0, 100}, {a, b}];
allPars = Flatten[Chop[ Table[{a, b}, {a, -0.8, 2.5, 0.1}, {b, -1.5, 1.5, 0.1}]], {1, 2}];; validPars = {}; invalidPars = {}; Table[If[Apply[pfun, par]["Domain"] === {{0.`, 100.`}}, AppendTo[validPars, par], AppendTo[invalidPars, par]], {par, allPars}]; ListPlot[{validPars, invalidPars}, PlotLegends -> {"Valid Parameters", "Invalid Parameters"}, PlotStyle -> {Directive[PointSize[0.015]]}] |
|
| Region of bounded solutions | Mathematica code |
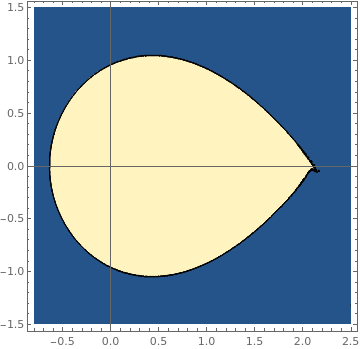
There is another approach:
|
fun1[a_?NumericQ, b_?NumericQ] := Module[
{res},
(* determine if domain is valid or invalid and return 1 or 0 respectively *) res = Quiet[pfun[a, b]]; Boole[res["Domain"] === {{0., 100.}}]; ]; ContourPlot[fun1[a, b], {a, -0.8, 2.5}, {b, -1.5, 1.5}, PlotPoints -> 50, MaxRecursion -> 3, Axes -> True, AxesOrigin -> {0, 0}] |
|
| Region of bounded solutions | Mathematica code |
|
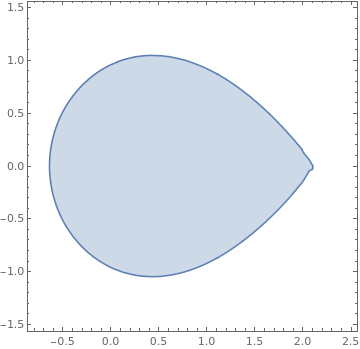
We make a region using the boolean function defined earlier
regionplot = RegionPlot[fun[a, b] >= 1, {a, -0.6, 2}, {b, -1, 1}]
|
|
| Region of bounded solutions | Mathematica code |

|
Create a boundary mesh from the region
mesh = BoundaryDiscretizeGraphics[regionplot]
|
|
| Boundary of the domain | Mathematica code |
|
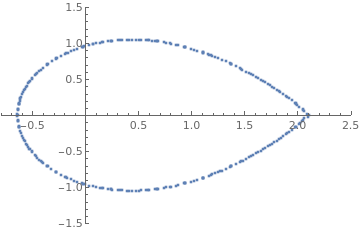
Now we generate the set of coordinates; however, they are not ordered. As you increase n using the slider, the curve fills up in random spots
Manipulate[
ListPlot[coord[[1 ;; n]], PlotRange -> {{-0.8, 2.5}, {-1.5, 1.5}}],
{{n, 50}, 1, Length[coord], 1}
]
|
|
| Boundary of the region | Mathematica code |
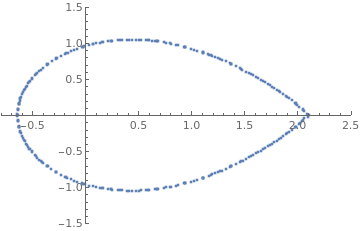
Next we sort the boundary coordinates.
MeshCells[] will give the lines that connect different points. Note that the arguments for Line[] are the coordinate indices (not the coordinate positions)
|
Use the slider below to see that the points are now ordered
Manipulate[
ListPlot[sortedcoord[[1 ;; n]],
PlotRange -> {{-0.8, 2.5}, {-1.5, 1.5}}],
{{n, 50}, 1, Length[sortedcoord], 1}
]
|
|
| The boundary of the domain, | Mathematica code |
Parametrizing the x- and y- coordinates separately in terms of pairs. Find the distance between each successive pair of points, and then the distances are added up cumulatively using
Accumulate[] (this will be the parameter for the x- and y- coordinates).
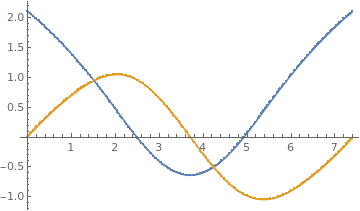
|
{px, py} = Transpose[{dist, #}] & /@ Transpose[sortedcoord];
{funca, funcb} = Interpolation[#, InterpolationOrder -> 1] & /@ {px, py}; Show[ Plot[{funca[p], funcb[p]}, {p, 0, dist[[-1]]}], ListPlot[{px, py}, PlotLegends -> {"\!\(\*SubscriptBox[\(p\), \ \(i\)]\),\!\(\*SubscriptBox[\(x\), \(i\)]\)", "\!\(\*SubscriptBox[\(p\), \(i\)]\),\!\(\*SubscriptBox[\(y\), \(i\ \)]\)"}] ] |
|
|
Plot of the boundary coordinates separately. |
Mathematica code |
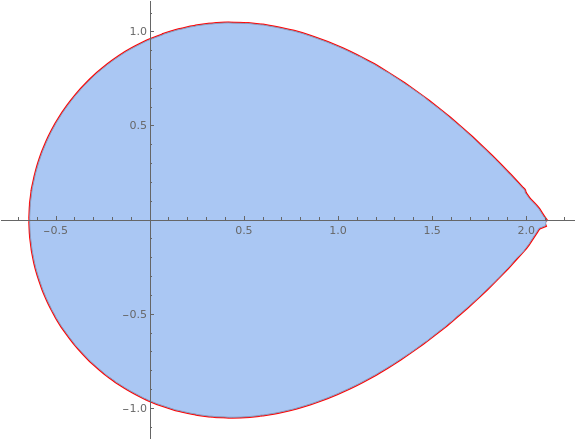
|
See the parametric plot of the interpolation function and compare to the region
Show[
ParametricPlot[{funca[p], funcb[p]}, {p, 0, dist[[-1]]},
PlotStyle -> {Thickness[0.005], Red}, ImageSize -> Large],
mesh
]
|
|
| The boundary of the domain, | Mathematica code |
Dependence on input values
ListPlot[divergentValues, AxesLabel -> {F, \[Omega]}]
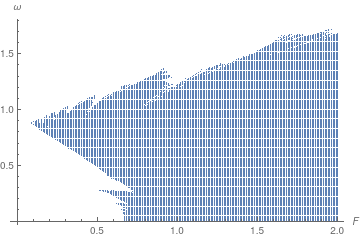
s = NDSolve[{x''[t]== -x[t] - x[t]^3 + 1*Cos[t], x[0]==1, x'[0]==0},x,{t,0,100}]
ParametricPlot[Evaluate[{x[t],x'[t]}/.s],{t,0,100}]
(* F = 1.5 *)
s2 = NDSolve[{x''[t]== -x[t] - x[t]^3 + 1.5*Cos[t], x[0]==1, x'[0]==0},x,{t,0,100}]
ParametricPlot[Evaluate[{x[t],x'[t]}/.s2],{t,0,100}]
(* F = 2.1 *)
s3 = NDSolve[{x''[t]== -x[t] - x[t]^3 + 2.1*Cos[t], x[0]==1, x'[0]==0},x,{t,0,100}]
ParametricPlot[Evaluate[{x[t],x'[t]}/.s3],{t,0,100}]
(* F = 3 *)
s4 = NDSolve[{x''[t]== -x[t] - x[t]^3 + 3*Cos[t], x[0]==1, x'[0]==0},x,{t,0,100}]
ParametricPlot[Evaluate[{x[t],x'[t]}/.s4],{t,0,100}]
(* omega = 2 *)
(* F = 1 *)
w = NDSolve[{x''[t]== -x[t] - x[t]^3 + 1*Cos[2*t], x[0]==1, x'[0]==0},x,{t,0,100}]
ParametricPlot[Evaluate[{x[t],x'[t]}/.w],{t,0,100}]
(* F = 0.5 *)
w2 = NDSolve[{x''[t]== -x[t] - x[t]^3 + 0.5*Cos[2*t], x[0]==1, x'[0]==0},x,{t,0,100}]
ParametricPlot[Evaluate[{x[t],x'[t]}/.w2],{t,0,100}]
(* F = 4.3 *)
w3 = NDSolve[{x''[t]== -x[t] - x[t]^3 + 4.3*Cos[2*t], x[0]==1, x'[0]==0},x,{t,0,100}]
ParametricPlot[Evaluate[{x[t],x'[t]}/.w3],{t,0,100}]
(* F = 5 *)
w4 = NDSolve[{x''[t]== -x[t] - x[t]^3 + 5*Cos[2*t], x[0]==1, x'[0]==0},x,{t,0,100}]
ParametricPlot[Evaluate[{x[t],x'[t]}/.w4],{t,0,100}]
- Hasting, C., Mischo, K., Morrison, M., Hands-on start to Wolftam Mathematica, 2020, third edition, WolframMedia.
Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations
Return to the Part 7 Special Functions