Return to computing page for the first course APMA0330
Return to computing page for the second course APMA0340
Return to Mathematica tutorial for the first course APMA0330
Return to Mathematica tutorial for the second course APMA0340
Return to the main page for the first course APMA0330
Return to the main page for the second course APMA0340
Return to Part VI of the course APMA0340
Introduction to Linear Algebra with Mathematica

Glossary

Applications

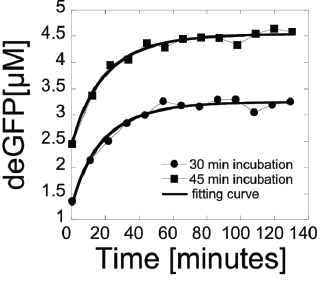
Example 1: A balance between protein and mRNA synthesis and degredation/inactivation can be modeled to help in laboratory testing of processes involving biological information. A certain study uses an E. coli cell-free expression system, where the informational elements (mRNA and proteins) are studied outside of the body and their respective cells. Testing processes in these conditions is key to developing new biological engineering applications.

In this example, we examine endogenous mRNA inactivation to better understand gene expression dynamics. The protein used is deGFP, which is a highly translatable green fluorescent protein. The following differential equations describe the rate of change over time of the concentration of deGFP mRNA (m), dark deGFP (deGFPd), and fluorescent deGFP (deGFPf).

\begin{align*} \frac{\text d}{{\text d} t}\, m(t) &= -B\,m(t) , \\ \frac{\text d}{{\text d} t}\,\mbox{deGRPd}(t) &= a\,m(t) -k\,\mbox{deGFPd} (t), \\ \frac{\text d}{{\text d} t} \,\mbox{deGFPf} (t)&= k\,\mbox{deGFPd}(t) . \end{align*} 
clear;
syms B m(t) deGFPd(t) a k deGFPf(t);
eqns=[diff(m)==-B*m;diff(deGFPd)==a*m-k*deGFPd;diff(deGFPf)==k*deGFPd]
The various constants are defined as the protein production rate a, the mRNA inactivation rate B, and the maturation time of the protein 1/k (including folding, etc). The following initial conditions are given in the study as the starting point for the respective assays:
\[ m(0) = \frac{1}{4}, \qquad \mbox{deGFPd} (0) = \frac{1}{4} , \qquad \mbox{deGFPf}(0) =0 . \] 
cond=[deGFPf(0)==0;deGFPd(0)==0.25;m(0)==0.25]
We solve the above differential equations using these initial conditions to find equations for the concentration of each item in terms of time. 
soln=dsolve([eqns;cond]);
deGFPd_(t)=soln.deGFPd
\[ \mbox{deGFPd} (t) = e^{-kt}\,\frac{B+a-k}{4\left( B-k \right)} - \frac{a}{4\left( B-k \right)} \, e^{-Bt} . \] 
m_(t)=soln.m
\[ m(t) = \frac{1}{4}\, e^{-Bt} . \] 
deGFPf_(t)=soln.deGFPf
\[ \mbox{deGFPf}(t) = \frac{B+a}{4\,B} - \frac{B+a-k}{4\left( B-k \right)}\, e^{-kt} + \frac{ak}{4B\left( B-k \right)}\, e^{-Bt} . \]
The study gives the final solved equation as
\[ [\mbox{deGFP}_f (t) = \frac{a\,m_0}{B\left( B-k \right)} \left( k\,e^{-Bt} - k +B - B\, e^{-kt} \right) . \]
where m0 is the concentration of active mRNA when transcription is ended. This equation is algebraically equivalent to the result given by MATLAB (once some higher order terms are removed). This model follows the collected data closely as shown on page 5 of Shin and Noireaux (2010).
Graphs of mRNA and proteins

Example 2: The differential equation governing the motion of a particle with electric charge q in an electromagnetic field is

\[ m\,\ddot{\bf r} = q \left( {\bf E} + {\bf v} \times {\bf B} \right) , \]
where m r, v, E, and B are, respectively, the mass of the particle, its position, its velocity, the electric field, and the magnetic field. This Lorentz force law (derived by Oliver Heaviside in 1889 a few years earlier than Hendrik Lorentz) can be written in component form as
\[ \begin{split} \ddot{x} (t) &= q \left( E_x + \dot{y}\, B_z - \dot{z}\, B_y \right) , \\ \ddot{y} (t) &= q \left( E_y + \dot{z}\, B_x - \dot{x}\, B_z \right) , \\ \ddot{z} (t) &= q \left( E_z + \dot{x}\, B_y - \dot{y}\, B_x \right) . \end{split} \]
We rewrite the above equation in vector form:
\[ \frac{{\text d}^2}{{\text d}t^2} \begin{bmatrix} x (t) \\ y(t) \\ z(t) \end{bmatrix} = q \begin{bmatrix} 0&B_z &-B_y \\ -B_z &0&B_x \\ B_y & -B_x &0 \end{bmatrix} \frac{{\text d}}{{\text d}t} \begin{bmatrix} x (t) \\ y(t) \\ z(t) \end{bmatrix} + q \begin{bmatrix} E_x \\ E_y \\ E_z \end{bmatrix} . \]

Example 3: Suppose that a ball of mass m is released with some initial velocity from a particular point over a surface. Then its position (x,y) is determined from the follwoing initial avlue problem

\[ \begin{split} \ddot{x} &= 0 , \\ \ddot{y} &= g , \end{split} \qquad \begin{bmatrix} x(0) \\ y(0) \end{bmatrix} = \begin{bmatrix} x0 \\ y0 \end{bmatrix} , \qquad \begin{bmatrix} \dot{x}(0) \\ \dot{y}(0) \end{bmatrix} = \begin{bmatrix} vx0 \\ vy0 \end{bmatrix} . \]
When the ball reaches the surface, it bounces back with velocity of k value of the original hit.

 

(*Calculates the position and velocity of the ball after one bounce \ on a given curve*)
OneBounce[k_, ramp_][{t0_, x0_, xp0_, y0_, yp0_}] :=
Module[{sol, t1, x1, xp1, y1, yp1, gramp, gp},
sol = First[ NDSolve[{x''[t] == 0, x'[t0] == xp0, x[t0] == x0, y''[t] == -9.8,
y'[t0] == yp0, y[t0] == y0}, {x, y}, {t, t0, Infinity},
Method -> {"EventLocator", "Event" :> y[t] - ramp[x[t]]},
MaxStepSize -> 0.01]];
t1 = InterpolatingFunctionDomain[x /. sol][[1, -1]];
{x1, xp1, y1, yp1} = Reflection[k, ramp][{x[t1], x'[t1], y[t1], y'[t1]} /. sol];
Sow[{x[t] /. sol, t0 <= t <= t1}, "X"];
Sow[{y[t] /. sol, t0 <= t <= t1}, "Y"];
Sow[{x1, y1}, "Bounces"];
{t1, x1, xp1, y1, yp1}]

 

(*Calculates the position and velocity of the ball after reflecting \ off of the curve*)
Reflection[k_, ramp_][{x_, xp_, y_, yp_}] :=
Module[{gramp, gp, xpnew, ypnew}, gramp = -ramp'[x];
If[Not[NumberQ[gramp]], Print["Could not compute derivative"];
Throw[$Failed]];
gramp = {-ramp'[x], 1};
If[gramp.{xp, yp} == 0, Print["No reflection"];
Throw[$Failed]];
gp = {1, -1} Reverse[gramp];
{xpnew, ypnew} = (k/(gramp.gramp)) (gp gp.{xp, yp} - gramp gramp.{xp, yp});
{x, xpnew, y, ypnew}]

 

(*Calculates the path of the ball over a specific range of x bounce \ by bounce and plots it*)
BouncingBall[k_, ramp_, {x0_, y0_}] :=
Module[{data, end, bounces, xmin, xmax, ymin, ymax}, If[y0 < ramp[x0], Print["Start above the ramp"];
Return[$Failed]];
data = Reap[Catch[Sow[{x0, y0}, "Bounces"];
NestWhile[OneBounce[k, ramp], {0, x0, 0, y0, 0}, Function[1 - #1[[1]] / #2[[1]] > 0.01], 2, 25]], _, Rule];
end = data[[1, 1]];
data = Last[data];
bounces = ("Bounces" /. data);
xmax = Max[bounces[[All, 1]]];
xmin = Min[bounces[[All, 1]]];
ymax = Max[bounces[[All, 2]]];
ymin = Min[bounces[[All, 2]]];
Show[{Plot[ramp[x], {x, xmin, xmax}, PlotRange -> {{xmin, xmax}, {ymin, ymax}}, AspectRatio -> (ymax - ymin) / (xmax - xmin)],
ParametricPlot[ Evaluate[{Piecewise["X" /. data], Piecewise["Y" /. data]}], {t, 0, end}, PlotStyle -> RGBColor[1, 0, 0]]}]]
Now we apply these subroutings to different surfaces.
ramp[x_] := If[x < 1, 1 - x, 0];
BouncingBall[.7, ramp, {0, 1.25}]
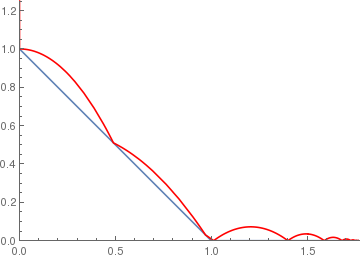(* 0.7 means the coefficient of rebouncing *)
circle[x_] := If[x < 1, Sqrt[1 - x^2], 0];
BouncingBall[.7, circle, {.1, 1.25}]
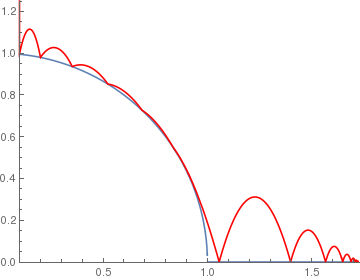wavyramp[x_] := If[x < 1, 1 - x + .05 Cos[11 Pi*x], 0];
BouncingBall[.75, wavyramp, {0, 1.25}]
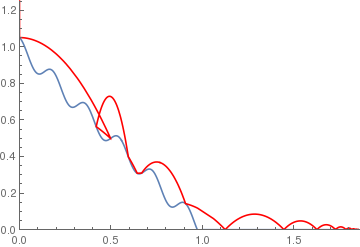(*Small slope linear with high friction*)

lowslopelr[x_] := If[x < 1, 1 - 0.1 x, 0];
BouncingBall[.5, lowslopelr, {0, 1.25}]
(*Sine wave ramp*)
sineramp[x_] := If[x < 5, 1 - .5 Sin[x], 0];
BouncingBall[.75, sineramp, {0, 1.25}]
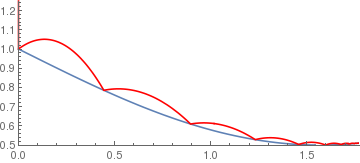arccosramp[x_] := If[-1 < x < 1, ArcCos[x], 0];
BouncingBall[.5, arccosramp, {-0.1, 2.3}]
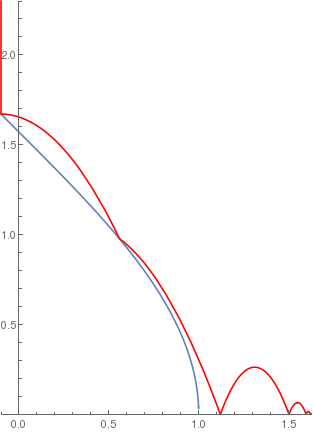(*Logarithmic ramp*)
logramp[x_] := If[x < 2, 2 - Log[x + 1], 0];
BouncingBall[.65, logramp, {0, 3}]
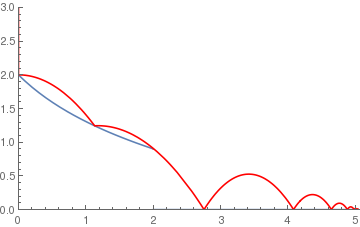(*Parabolic ramp*)
squareramp[x_] := If[x < 4, x^2, 0];
BouncingBall[.7, squareramp, {.5, 1}]
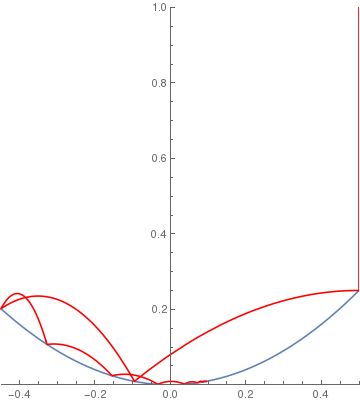(*Cubic ramp*)
cuberamp[x_] := If[-1 < x < 5, 4 (x^3) - x, 0];
BouncingBall[.9, cuberamp, {-0.25, .5}]
   ■

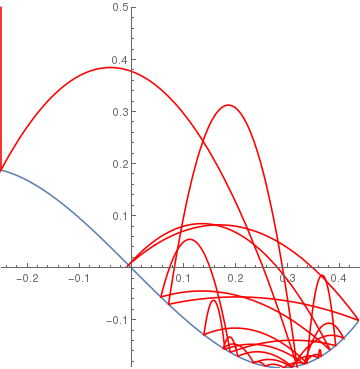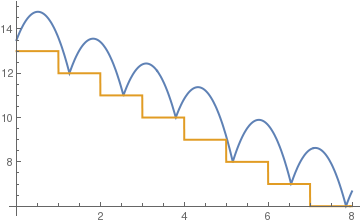
Example 4: Now we consider a bouncing ball on stairs.

(*standard stairs*)
c = .75;
sol = NDSolve[{y''[t] == -9.8, y[0] == 13.5, y'[0] == 5, a[0] == 13, WhenEvent[y[t] - a[t] == 0, y'[t] -> -c y'[t]], WhenEvent[Mod[t, 1], a[t] -> a[t] - 1]}, {y, a}, {t, 0, 8}, DiscreteVariables -> {a}];
Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 8}, PlotStyle -> Thick]
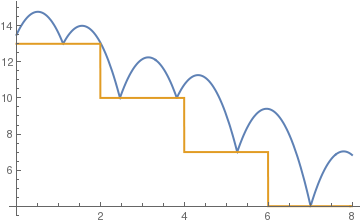
(*tall steps*)
c= .6;
sol = NDSolve[{y''[t] == -9.81, y[0] == 13.5, y'[0] == 5, a[0] == 13, WhenEvent[y[t] - a[t] == 0, y'[t] -> -c y'[t]], WhenEvent[Mod[t, 2], a[t] -> a[t] - 3]}, {y, a}, {t, 0, 8}, DiscreteVariables -> {a}];
Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 8}, PlotStyle -> Thick]
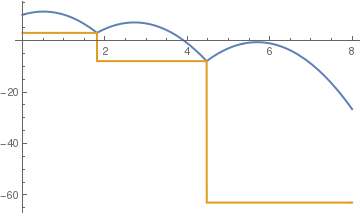
(*positive to negative steps*)
c = .5;
sol = NDSolve[{y''[t] == -9.81, y[0] == 10, y'[0] == 5, a[0] == 4, WhenEvent[y[t] == a[t], y'[t] -> -c y'[t]], WhenEvent[Mod[t, 2], a[t] -> 1 - a[t]], WhenEvent[ y[t] < a[t] , y''[t] = -y'[t]]}, {y, a}, {t, 0, 4}, DiscreteVariables -> {a}];
Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 8}, PlotStyle -> {Thick, Thick}]
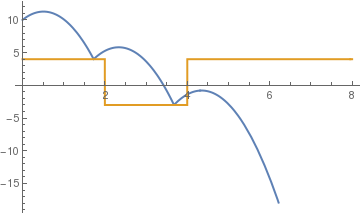   standard stairs    tall steps    positive to negative steps
(*corner to corner bounces (c)*)
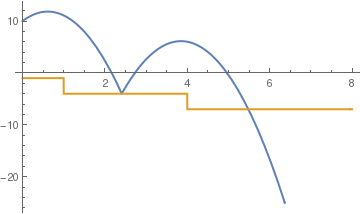
c= .7;
sol = NDSolve[{y''[t] == -9.81, y[0] == 10, y'[0] == 5, a[0] == 3, WhenEvent[y[t] == a[t], y'[t] -> -c y'[t]], WhenEvent[a[t] == y[t], a[t] -> 1 - (a[t])^2], WhenEvent[ y[t] < a[t] , y''[t] = -y'[t]]}, {y, a}, {t, 0, 10}, DiscreteVariables -> {a}];
Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 8}, PlotStyle -> {Thick, Thick}]

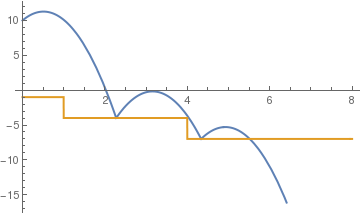
(*time based steps*)
c = .5;
sol = NDSolve[{y''[t] == -9.81, y[0] == 10, y'[0] == 5, a[0] == -1, WhenEvent[y[t] == a[t], y'[t] -> -c y'[t]], WhenEvent[t == -a[t], a[t] -> a[t] - 3], WhenEvent[ y[t] < a[t] , y''[t] = -y'[t]]}, {y, a}, {t, 0, 5}, DiscreteVariables -> {a}];
Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 8}, PlotStyle -> {Thick, Thick}]

c = 0.8;
sol = NDSolve[{y''[t] == -9.81, y[0] == 10, y'[0] == 6, a[0] == -1, WhenEvent[y[t] == a[t], y'[t] -> -c y'[t]], WhenEvent[t == -a[t], a[t] -> a[t] - 3], WhenEvent[ y[t] < a[t] , y''[t] = -y'[t]]}, {y, a}, {t, 0, 5}, DiscreteVariables -> {a}];
Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 8}, PlotStyle -> {Thick, Thick}]
   corner to corner bounces    time based steps    elastic bounce
   ■

 

Return to Mathematica page
Return to the main page (APMA0340)
Return to the Part 1 Matrix Algebra
Return to the Part 2 Linear Systems of Ordinary Differential Equations
Return to the Part 3 Non-linear Systems of Ordinary Differential Equations
Return to the Part 4 Numerical Methods
Return to the Part 5 Fourier Series
Return to the Part 6 Partial Differential Equations