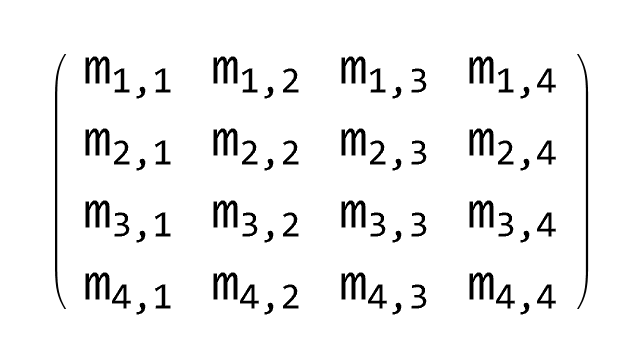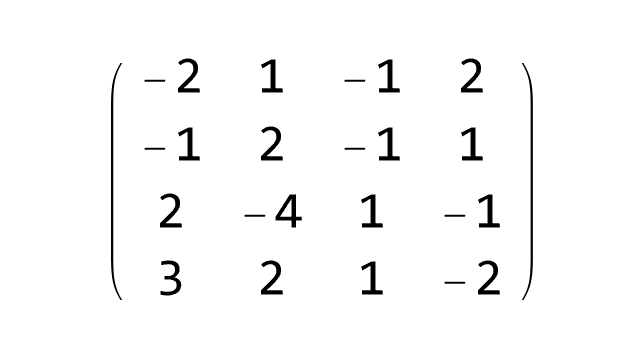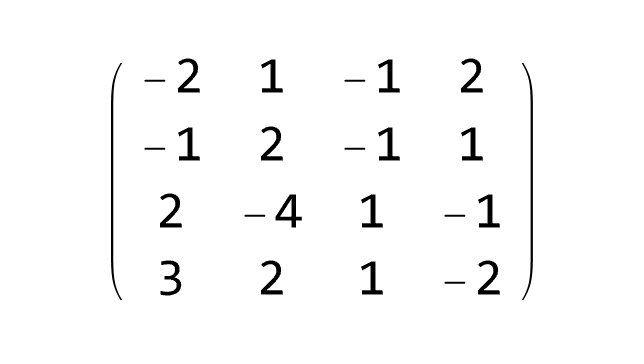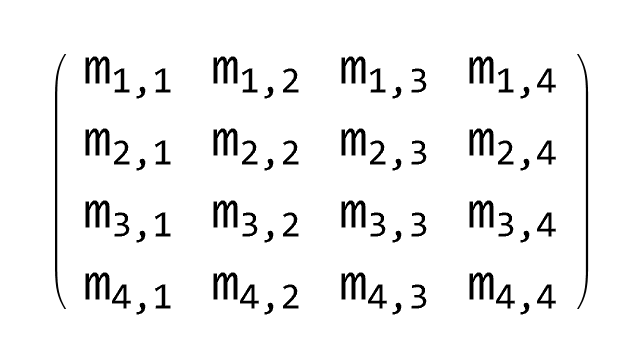Rank Estimations
The rank of a matrix is the order of the highest
order sub-matrix having non-zero determinant.
Theorem 1:
Rank of matrix posseses the following properties.
- Let A be an m × n matrix. Then rank(A) ≤ min{m, n}.
- Only zero matrix has rank zero.
- A square matrix A of size n×n is invertible if and only if . rank(A) = n.
- Rank(A + B) ≤ rank(A) + rank(B).
- Rank(A) = rank(AT) = rank(ATA).
- Rank(kL/i>A) = rank(A) if k ≠ 0.
Example 5:
■
End of Example 5
Theorem 2 (Sylvester):
If A is an m × n matrix and B is an n × p matrix, then
\[
\mbox{rank}\left( \mathbf{A} \right) + \mbox{rank}\left( \mathbf{B} \right) -n \leslant \mbox{rank}\left( \mathbf{A}\,\mathbf{B} \right) \leslant \min \left\{ \mbox{rank}\left( \mathbf{A} \right) \ , \ \mathbf{B} \right) \right\} .
\]
Example 5:
■
End of Example 5
Theorem 3 (robenius):
Let A, B, and . C be any matrices such that A B, B C, and ABC exists, then
\[
\mbox{rank}\left( \mathbf{A}\,\mathbf{B} \right) + \mbox{rank}\left( \mathbf{B}\,\mathbf{C} \right) \leslant \mbox{rank}\left( \mathbf{A}\,\mathbf{B}\,\mathbf{C} \right) + \mbox{rank}\left( \mathbf{B} \right) .
\]
Example 5:
■
End of Example 5
- Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.