es

The Wolfram Mathematic notebook which contains the code that produces all the Mathematica output in this web page may be downloaded at this link. Caution: This notebook will evaluate, cell-by-cell, sequentially, from top to bottom. However, due to re-use of variable names in later evaluations, once subsequent code is evaluated prior code may not render properly. Returning to and re-evaluating the first Clear[ ] expression above the expression no longer working and evaluating from that point through to the expression solves this problem.

$Post := If[MatrixQ[#1], MatrixForm[#1], #1] & (* outputs matricies in MatrixForm*)
Remove[ "Global`*"] // Quiet (* remove all variables *)

Solving A x = b

Theorem (Kronecker--Capelli): A system of linear algebraic equations A x = b has a solution if and only if the matrix A has the same rank as the augmented matrix \( \left[ {\bf A} \,|\,{\bf b} \right] . \) ■

It is obvious that the rank of the augmented matrix \( \left[ {\bf A} \,|\,{\bf b} \right] \) is greater than or equal to the rank of the matrix A. They are equal if and only if b is a linear combination of the columns of the matrix A. The last condition is equivalent to the statement that there exists a vector x such that A x = b. ■
   
Example 1:    ■
End of Example 1

Theorem (Fredholm matrix Theorem): A system of linear algebraic equations A x = b has a solution if and only if b is orthogonal to every solution of the homogeneous equation z A = 0, that is, their inner product is zero: \( {\bf z} \cdot {\bf b} = 0 . \) In other words, the input vector b must be orthogonal to every solution of the homogeneous adjoint equation \( {\bf A}^{\ast} {\bf y} = {\bf 0} , \) which means that \( {\bf y} \perp {\bf b} \quad \Longleftrightarrow \quad {\bf y} \cdot {\bf b} =0 . \) ■

Sufficiency Proof: Let r be the rank of matrix A. We can assume without any loss of generality that the first r rows of the matrix A are linearly independent. Then obviously the first r rows of the augmented matrix will be also linearly independent too. If the k-th row of the matrix A is a linear combination of the first r rows of A, then there exists a nonzero vector z such that z A = 0. According to hypothesis of theorem, \( {\bf z} \cdot {\bf b} = 0 . \) This implies that the k-th row of the augmented matrix \( \left[ {\bf A} \,|\,{\bf b} \right] \) is a linear combination of the first r rows of the augmented matrix. So ranks of A and the augmented matrix are the same. According to Kronecker-Capelli theorem, the linear system of equations A x = b is consistent.

Necessity Proof: Suppose that the linear system A x = b has a solution. Then for every \( {\bf z} \in \mathbb{C}^m \) we have the equality

\[ {\bf z} \, {\bf A} \, {\bf x} = {\bf z} \, {\bf b} . \]
If z A = 0, then z b = 0.
   
Example 2: The span of the empty set \( \varnothing \) consists of a unique element 0. Therefore, \( \varnothing \) is linearly independent and it is a basis for the trivial vector space consisting of the unique element---zero. Its dimension is zero.    ■
End of Example 2

 

Example: In \( \mathbb{R}^n , \) the vectors \( e_1 [1,0,0,\ldots , 0] , \quad e_2 =[0,1,0,\ldots , 0], \quad \ldots , e_n =[0,0,\ldots , 0,1] \) form a basis for n-dimensional real space, and it is called the standard basis. Its dimension is n.

 

Example: Let us consider the set of all real \( m \times n \) matrices, and let \( {\bf M}_{i,j} \) denote the matrix whose only nonzero entry is a 1 in the i-th row and j-th column. Then the set \( {\bf M}_{i,j} \ : \ 1 \le i \le m , \ 1 \le j \le n \) is a basis for the set of all such real matrices. Its dimension is mn.

 

Example: The set of monomials \( \left\{ 1, x, x^2 , \ldots , x^n \right\} \) form a basis in the set of all polynomials of degree up to n. It has dimension n+1. ■

 

 

A vector space is called finite-dimensional if it has a basis consisting of a finite
number of elements. The unique number of elements in each basis for V is called
the dimension of V and is denoted by dim(V). A vector space that is not finite-
dimensional is called infinite-dimensional.

  The next example demonstrates how Mathematica can determine the basis or set of linearly independent vectors from the given set. Note that basis is not unique and even changing the order of vectors, a software can provide you another set of linearly independent vectors.

Example: Suppose we are given four linearly dependent vectors:

MatrixRank[m = {{1, 2, 0, -3, 1, 0}, {1, 2, 2, -3, 1, 2}, {1, 2, 1, -3, 1, 1}, {3, 6, 1, -9, 4, 3}}]
Out[1]= 3

Then each of the following scripts determine a subset of linearly independent vectors:

m[[ Flatten[ Position[#, Except[0, _?NumericQ], 1, 1]& /@
Last @ QRDecomposition @ Transpose @ m ] ]]
Out[2]= {{1, 2, 0, -3, 1, 0}, {1, 2, 2, -3, 1, 2}, {3, 6, 1, -9, 4, 3}}

or, using subroutine

MinimalSublist[x_List] :=
Module[{tm, ntm, ytm, mm = x}, {tm = RowReduce[mm] // Transpose,
ntm = MapIndexed[{#1, #2, Total[#1]} &, tm, {1}],
ytm = Cases[ntm, {___, ___, d_ /; d == 1}]};
Cases[ytm, {b_, {a_}, c_} :> mm[[All, a]]] // Transpose]

we apply it to our set of vectors.

m1 = {{1, 2, 0, -3, 1, 0}, {1, 2, 1, -3, 1, 2}, {1, 2, 0, -3, 2, 1}, {3, 6, 1, -9, 4, 3}};
MinimalSublist[m1]
Out[3]= {{1, 0, 1}, {1, 1, 1}, {1, 0, 2}, {3, 1, 4}}

In m1 you see 1 row and n columns together,so you can transpose it to see it as column {{1, 1, 1, 3}, {0, 1, 0, 1}, {1, 1, 2, 4}}

One can use also the standard Mathematica command: IndependenceTest. ■

 

Fredholm's finite-dimensional alternative

First, we need to recall some definitions.

Let f : X ⇾ Y be a linear mapping of vector space X into another vector space Y, both are over the same field 𝔽. Its coimage and cokernel are defined as \[ \mbox{coimage} \left( f \right) = \mbox{coim} \left( f \right) = X / \mbox{ker}(f) \] and \[ \mbox{coker} \left( f \right) = Y / \mbox{im}\left( f \right) , \] respectively.
There exists a chain of linear mappings, which "partition f:"
\[ \mbox{ker} \left( f\right) \stackrel{i}{\longrightarrow} X \stackrel{\sigma}{\longrightarrow} \mbox{coimage} \left( f \right) \stackrel{h}{\longrightarrow} \mbox{im} \left( f \right) \stackrel{j}{\longrightarrow} Y \stackrel{g}{\longrightarrow} \mbox{coker} \left( f \right) , \]
where all mappings, except h, are canonical insertions and factorizations, while h is the only mapping that completes the commutative diagram
xr = Graphics[{Blue, Thickness[0.01], Arrowheads[0.1], Arrow[{{0.04, 1}, {0.3, 0.5}}]}]; xl = Graphics[{Blue, Thickness[0.01], Arrowheads[0.1], Arrow[{{-0.04, 1}, {-0.3, 0.5}}]}]; xh = Graphics[{Blue, Thickness[0.01], Arrowheads[0.1], Arrow[{{-0.2, 0.44}, {0.25, 0.44}}]}]; txt = Graphics[{Text[Style["X", Black, Bold, 20], {0, 1.05}], Text[Style["coim(f)", Black, Bold, 20], {-0.29, 0.44}], Text[Style["im(f)", Black, Bold, 20], {0.33, 0.44}]}]; txt2 = Graphics[{Text[Style["h", Black, 22], {0, 0.5}], Text[Style["c", Black, 22], {-0.2, 0.85}], Text[Style["f", Black, 22], {0.2, 0.85}]}]; Show[xr, xl, xh, txt, txt2]
Figure 1: mapping diagram

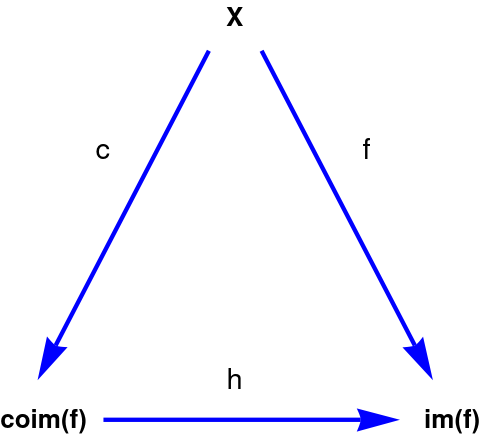
It is unique, because ker(c) = kerf, and it is an isomorphism, because the inverse mapping also exists and is defined uniquely. The point of uniting these spaces into pairs (with and without the prefix "co") is explained in the theory of duality.

Let f : X ⇾ Y be a linear mapping of vector space X into another vector space Y, both are over the same field 𝔽. The difference of dimensions \[ \mbox{ind}\left( f \right) = \dim\,\mbox{coker}}\left( f \right) - \dim\,\mbox{ker}}\left( f \right) \] is called the index of the operator/transformation f.

In particular, if dimX = dimY = n < ∞, then for any linear operator f on X, indf = 0. This implies the so-called Fredholm alternative:

Theorem (Fredholm matrix Theorem): A system of linear algebraic equations A x = b has a solution if and only if b is orthogonal to every solution of the homogeneous equation z A = 0, that is, their inner p either the equation g(x) = y is solvable for all y and then the equation g(x) = 0 has only zero solutions; or this equation cannot be solved for all y and then the homogeneous equation g(x) = 0 has non-zero solutions. More precisely, if ind g = 0, then the dimension of the space of solutions of the homogeneous equation equals the codimension of the spaces on the right hand sides for which the inhomogeneous equation is solvable.

 

 

  1. Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
  2. Halmos, Paul Richard (1974) [1958]. Finite-Dimensional Vector Spaces (2nd ed.). Springer. ISBN 0-387-90093-4.
  3. Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
  4. Treil, S., Linear Algebra Done Wrong.
  5. Wikipedia, Dual space/